第三章勾股定理 单元测试题 (无答案) 鲁教版(五四制)七年级数学上册
文档属性
| 名称 | 第三章勾股定理 单元测试题 (无答案) 鲁教版(五四制)七年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 133.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-21 00:00:00 | ||
图片预览


文档简介
第三章勾股定理+单元测试题(1) 鲁教版数学七年级上册
一、选择题
1.下列四组数据中,不能作为直角三角形三边长的是
A. ,, B.
C. ,, D. ,,
2.小明在一个长方形的水池里游泳,长方形的长和宽分别为,,小明在水池中沿直线最远可以游
A. B. C. D.
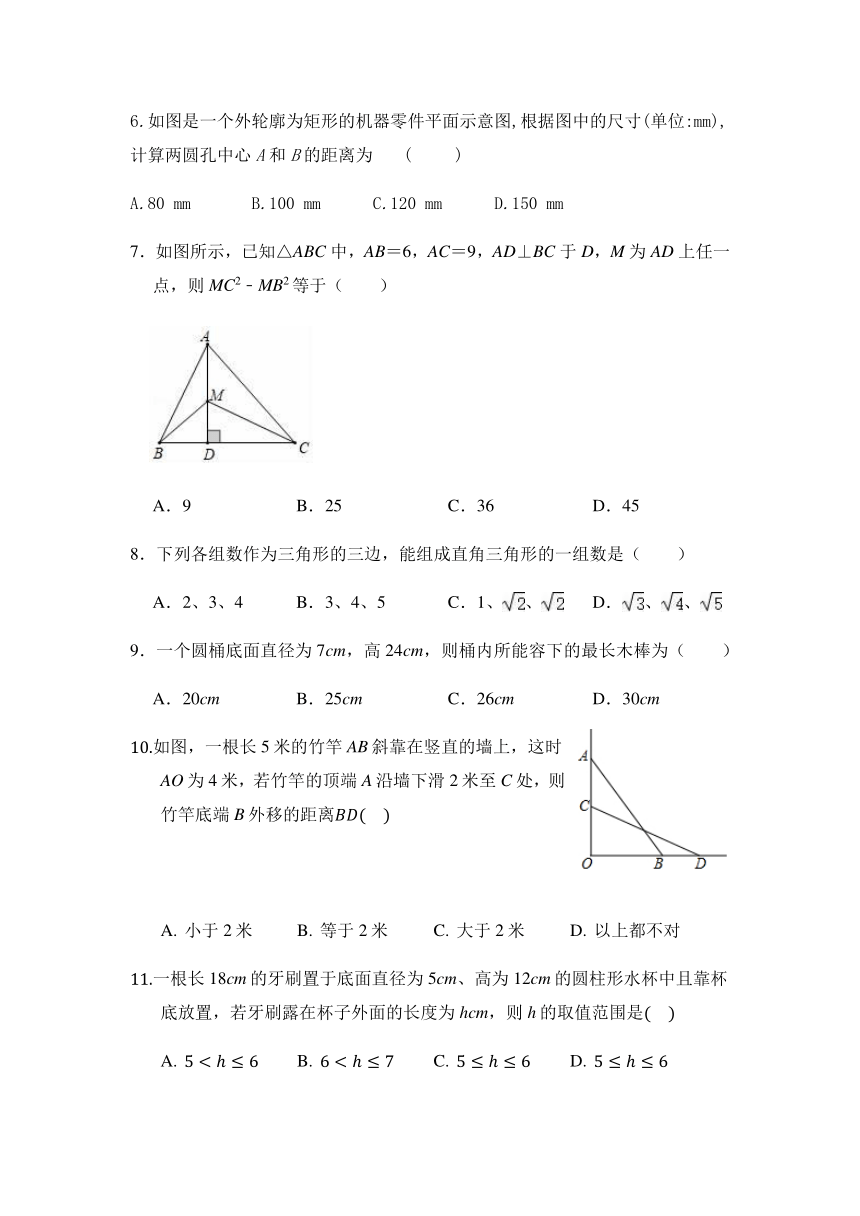
3.如图是一个三级台阶,每一级的长、宽、高分别为,,和是这个台阶上两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点的最短路程为
A. B. C. D.
4.三角形的三边长满足(b+c)2=a2+2bc,则这个三角形是 ( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
5.如图,是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别是a,b,则(a+b)2= ( )
A.13 B.19 C.25 D.169
3. 5. 6.
6.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为 ( )
A.80 mm B.100 mm C.120 mm D.150 mm
7.如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2﹣MB2等于( )
A.9 B.25 C.36 D.45
8.下列各组数作为三角形的三边,能组成直角三角形的一组数是( )
A.2、3、4 B.3、4、5 C.1、、 D.、、
9.一个圆桶底面直径为7cm,高24cm,则桶内所能容下的最长木棒为( )
A.20cm B.25cm C.26cm D.30cm
10.如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离
A. 小于2米 B. 等于2米 C. 大于2米 D. 以上都不对
11.一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中且靠杯底放置,若牙刷露在杯子外面的长度为hcm,则h的取值范围是
A. B. C. D.
12.如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知,于A,于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EA的长是
A. 4 B. 5 C. 6 D.
二填空题
13、已知两条线段的长为5和4,当第三条线段的长的平方为________时,这三条线段能组成一个直角三角形.
14、把一根12厘米长的铁丝,从一端起顺次截下3厘米和5厘米的两根铁丝,用这三条铁丝摆成的三角形面积是 ________.
15、数组3、4、5;5、12、13;7、24、25;9、40、41;……都是勾股数,若n为直角三角形的一较长直角边,用含n的代数式表示斜边为________.
16、一个长方形院子要在三面建砖墙,院子的对角线长比一面砖墙长2m,另外的两面砖墙都是长10m,则三面砖墙共长________米.
17.如图所示的圆柱体中底面圆的半径是,高为12,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,CD、AB分别为上、下两底的直径,且CD∥AB,则小虫爬行的最短路程是 .
18.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
三、解答题(共55分)
19.如图,在△ABC中,∠C=90°,D是BC的中点,AB=10,AC=6.求AD2的值.
20.如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求AB的长.
21.如图,在△ABC中,AB=AC,E是AC上的一点,CE=5,BC=13,BE=12.
(1)判断△ABE的形状,并说明理由;
(2)求线段AB的长.
22如图,某火车站内部墙面MN上有破损处(看作点A),现维修师傅需借助梯子DE完成维修工作.梯子的长度为5 m,将其斜靠在这面墙上,测得梯子底部E离墙角N处3 m,维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D距离墙面破损处1 m.
(1)该火车站墙面破损处A距离地面有多高
(2)如果维修师傅要使梯子顶部到地面的距离为4.8 m,那么梯子底部需要向墙角方向移动多少米
23.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2EF,则正方形ABCD的面积为 .
24.如图,∠BAC=90°,BC=28,AC=14,BD=13,AD=15.
(1)求AB的长度;
(2)作DH⊥AB,并求△ADB的面积.
25.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
一、选择题
1.下列四组数据中,不能作为直角三角形三边长的是
A. ,, B.
C. ,, D. ,,
2.小明在一个长方形的水池里游泳,长方形的长和宽分别为,,小明在水池中沿直线最远可以游
A. B. C. D.
3.如图是一个三级台阶,每一级的长、宽、高分别为,,和是这个台阶上两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点的最短路程为
A. B. C. D.
4.三角形的三边长满足(b+c)2=a2+2bc,则这个三角形是 ( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
5.如图,是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别是a,b,则(a+b)2= ( )
A.13 B.19 C.25 D.169
3. 5. 6.
6.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为 ( )
A.80 mm B.100 mm C.120 mm D.150 mm
7.如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2﹣MB2等于( )
A.9 B.25 C.36 D.45
8.下列各组数作为三角形的三边,能组成直角三角形的一组数是( )
A.2、3、4 B.3、4、5 C.1、、 D.、、
9.一个圆桶底面直径为7cm,高24cm,则桶内所能容下的最长木棒为( )
A.20cm B.25cm C.26cm D.30cm
10.如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离
A. 小于2米 B. 等于2米 C. 大于2米 D. 以上都不对
11.一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中且靠杯底放置,若牙刷露在杯子外面的长度为hcm,则h的取值范围是
A. B. C. D.
12.如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知,于A,于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EA的长是
A. 4 B. 5 C. 6 D.
二填空题
13、已知两条线段的长为5和4,当第三条线段的长的平方为________时,这三条线段能组成一个直角三角形.
14、把一根12厘米长的铁丝,从一端起顺次截下3厘米和5厘米的两根铁丝,用这三条铁丝摆成的三角形面积是 ________.
15、数组3、4、5;5、12、13;7、24、25;9、40、41;……都是勾股数,若n为直角三角形的一较长直角边,用含n的代数式表示斜边为________.
16、一个长方形院子要在三面建砖墙,院子的对角线长比一面砖墙长2m,另外的两面砖墙都是长10m,则三面砖墙共长________米.
17.如图所示的圆柱体中底面圆的半径是,高为12,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,CD、AB分别为上、下两底的直径,且CD∥AB,则小虫爬行的最短路程是 .
18.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
三、解答题(共55分)
19.如图,在△ABC中,∠C=90°,D是BC的中点,AB=10,AC=6.求AD2的值.
20.如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求AB的长.
21.如图,在△ABC中,AB=AC,E是AC上的一点,CE=5,BC=13,BE=12.
(1)判断△ABE的形状,并说明理由;
(2)求线段AB的长.
22如图,某火车站内部墙面MN上有破损处(看作点A),现维修师傅需借助梯子DE完成维修工作.梯子的长度为5 m,将其斜靠在这面墙上,测得梯子底部E离墙角N处3 m,维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D距离墙面破损处1 m.
(1)该火车站墙面破损处A距离地面有多高
(2)如果维修师傅要使梯子顶部到地面的距离为4.8 m,那么梯子底部需要向墙角方向移动多少米
23.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2EF,则正方形ABCD的面积为 .
24.如图,∠BAC=90°,BC=28,AC=14,BD=13,AD=15.
(1)求AB的长度;
(2)作DH⊥AB,并求△ADB的面积.
25.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
