七年级数学下册沪科版 期末测试卷(含答案)
文档属性
| 名称 | 七年级数学下册沪科版 期末测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 287.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-21 18:43:49 | ||
图片预览




文档简介
期末测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.在,,,,这五个数中,无理数的个数为( )
A.2 B.3 C.4 D.5
2.下列计算不正确的是( )
A. B.
C. D.
3.如图,在中,,,点在上,,将线段沿着方向平移得到线段,点,分别落在,边上,则的周长为( )
A. B. C. D.
4.已知关于的分式方程的解为整数,则符合条件的整数可以是( )
A.1 B.2 C.3 D.5
5.若关于x的不等式组有且仅有四个整数解,且关于y的一元一次方程的解为正整数,则符合条件的所有整数m的和为( )
A.-2 B.5 C.9 D.10
6.如图,,,则α、β、γ的关系是( )
B.
C. D.
7.一块麦田m亩,甲收割完这块麦田需n小时,乙比甲少用0.5小时就能收割完这块麦田,两人一起收割完这块麦田需要的时间是( )
A. B. C. D.
8.对于实数p,我们规定:用表示不小于的最小整数.例如:,,现在对72进行如下操作:72 ,即对72只需进行3次操作后变为2.类比上述操作:对512只需进行( )次操作后变为2.
A.3 B.4 C.5 D.6
9.的三边分别为a,b,c,且满足,则的形状为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
10.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EFHC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①ADBC;②GK平分∠AGC;③∠DGH=37°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题,满分18分,每小题3分)
11.已知.
(1)x的值为_____;
(2)x的算术平方根为_____.
12.已知关于x的不等式组的所有整数解的和为,m的取值范围是_________ .
13.若,且,则的值是_________.
14.一个角的两边分别与另一个角的两边垂直,且其中一个角为50°,则另一个角的度数是______________.
15.如图,,BC平分,设为,点E是射线BC上的一个动点,若,则的度数为__________.(用含的代数式表示).
16.若是完全平方式,则的值为______.
三.解答题(共7小题,满分52分)
17.(6分)解不等式(组)
(1) (2)
18.(6分)(1)计算:;
(2)分解因式:.
19.(8分)(1)先化简,在求值:,再从、0、1三个数中选择一个你认为合适的数作为的值代入求值,
(2)解方程:
20.(8分)因式分解:
(1); (2); (3)
21.(8分)两个工程队共同参与一项筑路工程,甲队单独施工30天完成总工程的,这时增加了乙队,两队又共同工作了15天,完成全部工程.
(1)求乙队单独施工多少天完成全部工程?
(2)若甲队工作4天,乙队工作3天共需支付工程劳务费42000元,甲队工作5天,乙队工作6天共需支付工程劳务费75000元,求甲、乙两队工作一天的劳务费分别为多少元?
(3)在(2)的条件下,若两个工程队不同时施工,在总劳务费不超过28万元的情况下,则最快______天能完成总工程.
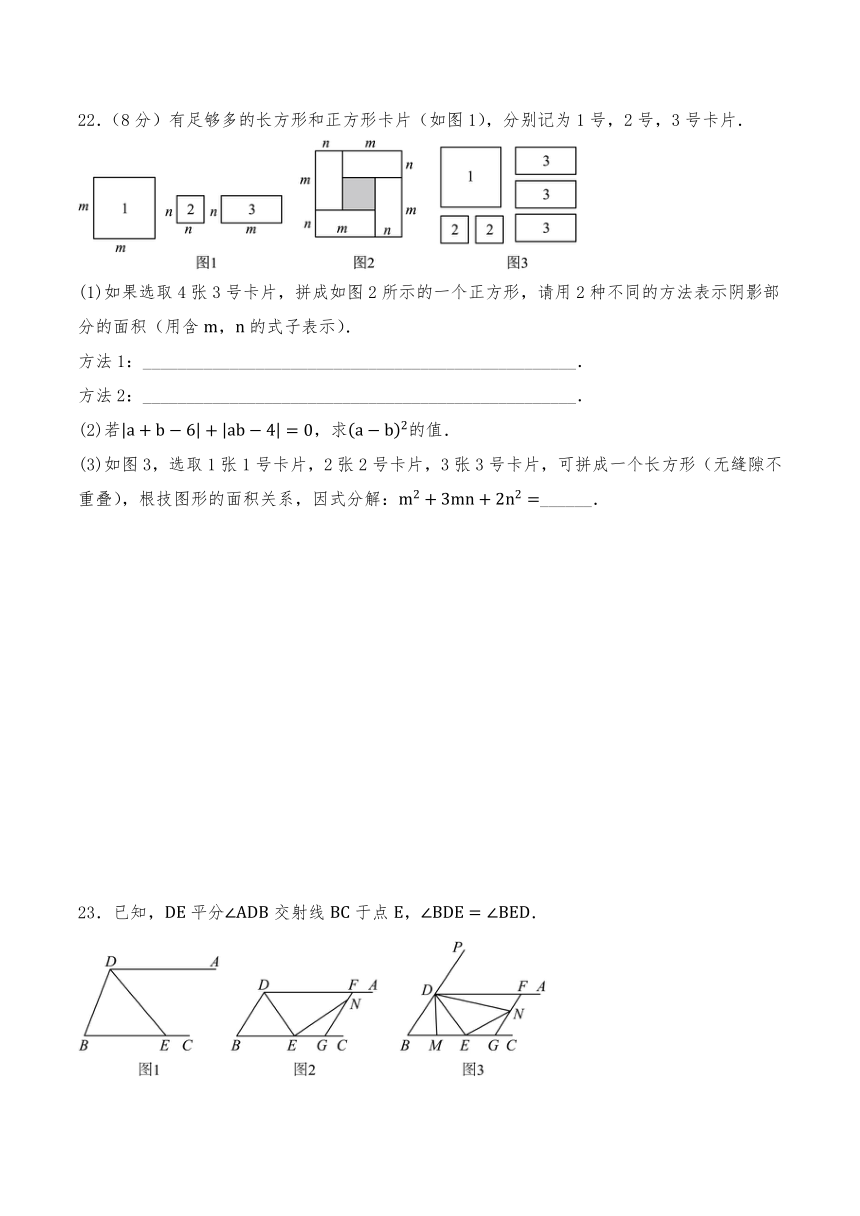
22.(8分)有足够多的长方形和正方形卡片(如图1),分别记为1号,2号,3号卡片.
(1)如果选取4张3号卡片,拼成如图2所示的一个正方形,请用2种不同的方法表示阴影部分的面积(用含,的式子表示).
方法1:__________________________________________________.
方法2:__________________________________________________.
(2)若,求的值.
(3)如图3,选取1张1号卡片,2张2号卡片,3张3号卡片,可拼成一个长方形(无缝隙不重叠),根技图形的面积关系,因式分解:______.
23.已知,平分交射线于点,.
(1)如图1,求证:;
(2)如图2,点是射线上一点,过点作交射线于点,点是上一点,连接,求证:;
(3)如图3,在(2)的条件下,连接,点为延长线上一点,平分交于点,若平分,,,求的度数.
答案解析
选择题
1.A
【分析】根据无理数的定义判断即可.
【详解】解:在,,,,这五个数中,无理数有、共2个.
故选A.
2.C
【分析】根据同底数幂乘除法、合并同类项、积的乘方以及幂的乘方进行计算即可.
【详解】解:A、,原式计算正确,不符合题意;
B、,原式计算正确,不符合题意;
C、,原式计算错误,符合题意;
D、,原式计算正确,不符合题意;
故选:C.
3.C
【分析】根据平移的性质得到线段之间的等量关系,然后将的每条边长度分别求出计算即可.
【详解】解: ,
,
由平移可知:,,
,
,
,
,
,
,
的周长.
故选C
4.B
【分析】解该分式方程得,结合该分式方程的解为整数和分式有意义的条件,即得出为2的倍数且,即选B.
【详解】解:,
方程两边同时乘,得:,
解得:,
∵该分式方程的解为整数,
∴为2的倍数,
∴为2的倍数.
∵,
∴,
∴,
∴,
综上可知为2的倍数且.
∴只有B选项符合题意.
故选B.
5.B
【分析】表示出不等式组的解集,由不等式组有且只有4个整数解确定的取值范围,再由方程的解为正整数,求出满足条件的整数m,从而求解;
【详解】解:由
得:,
由不等式组有且仅有4个整数解,得到
,
解得:,
即整数,
解方程,
得:
因为关于y的一元一次方程的解为正整数
所以,
故整数m的和为5,
故选择:B
6.C
【分析】过点C、D分别作的平行线、,利用平行线的性质即可解决问题.
【详解】解:如图,过点C、D分别作的平行线、,
∵,
∴,
∴,,,
∵,,
∴,
∴.
故选:C.
7.A
【分析】先得到乙收割完这块麦田需要的时间,根据工作总量÷工作时间=工作效率,分别求出甲、乙的工作效率,再用工作总量÷甲、乙的工作效率和求出两人一起收割完这块麦田需要的工作时间.
【详解】乙收割完这块麦田需要的时间是 小时,
甲的工作效率是(亩/小时),
乙的工作效率 (亩/小时),
故两人一起收割完这块麦田需要的工作时间为 小时,
答:两人一起收割完这块麦田需要 小时.
故选A.
8.B
【分析】仿照题目已知的例题即可解答.
【详解】解:由题意得:
512 ,
∴对512只需进行4次操作后变为2;
故选:B.
9.B
【分析】先将a2﹣b2+ac﹣bc进行因式分解,可得a﹣b=0,进一步即可判断△ABC的形状.
【详解】解:∵a2﹣b2+ac﹣bc
=(a+b)(a﹣b)+c(a﹣b)
=(a+b+c)(a﹣b)=0,
∵a+b+c>0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形,
故选:B.
10.B
【分析】根据平行线的判定定理得到AD∥BC,故①正确;由平行线的性质得到∠AGK=∠CKG,等量代换得到∠AGK=∠CGK,求得GK平分∠AGC;故②正确;根据题意列方程得到∠FGA=∠DGH=37°,故③正确;设∠AGM=α,∠MGK=β,得到∠AGK=α+β,根据角平分线的定义即可得到结论.
【详解】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
∵∠FGA的余角比∠DGH大16°,
∴90°-∠FGA -∠DGH=16°,
∵∠FGA=∠DGH,
∴90°-2∠FGA=16°,
∴∠FGA=∠DGH=37°,故③正确;
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二.填空题
11.
【分析】(1)利用立方根的定义求得x的值;
(2)利用算术平方根的定义解答即可.
【详解】解:(1)∵,
∴,
∴x=3,
故答案为:3;
(2)由(1)知x=3,
3的算术平方根为,
故答案为:.
12.或
【分析】先求出不等式组的解集,然后根据不等式组的整数解的情况得到不等式组的整数解可以为、或、、、、、0、1、2、3,据此求解即可解答.
【详解】,
解不等式①得:,
解不等式②得:,
不等式组的解集为:,
不等式组的所有整数解的和为,
不等式组的整数解可以为、或、、、、、0、1、2、3,
或,
或,
故答案为:或.
13.
【分析】已知等式变形后,代入原式计算即可得到结果.
【详解】解∶,且,
,
原式.
故答案为∶.
14.50°或130°
【分析】此题可以通过两个图形得出这两个角的关系相等或互补.
【详解】如图:
图1中,根据垂直的量相等的角都等于90°,对顶角相等,
∴∠1=∠2=50°,
图2中,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,∴∠1+∠2=360°-90°-90°=180°.
∴∠2=130°
故答案为:50°或130°.
15.或
【分析】根据题意可分两种情况,①若点运动到上方,根据平行线的性质由可计算出的度数,再根据角平分线的性质和平行线的性质,计算出的度数,再由,,列出等量关系求解即可得出结论;②若点运动到下方,根据平行线的性质由可计算出的度数,再根据角平分线的性质和平行线的性质,计算出的度数,再由,列出等量关系求解即可得出结论.
【详解】解:如图,若点E运动到l1上方,
,
,
平分,
,
,
又,
,
,
解得;
如图,若点E运动到l1下方,
,
,
平分,
,
,
又,
,
,
解得.
综上的度数为或.
故答案为:或.
16.或
【分析】根据完全平方公式的特点:首平方,尾平方,首尾两数积的两倍在中央求解即可.
【详解】解:∵是完全平方式,
∴,
整理得:或,
解得或,
故答案为:或.
三.解答题
17.(1)解:移项合并同类项得,
,
系数化为1得,
,
∴不等式解集为;
(2)解:解不等式①得,
,
解不等式②得,
,
∴不等式组解集为:.
18.(1)原式
.
(2)原式
.
19.(1)解:原式
,
要使分式有意义,不能取,1,
则当时,原式.
(2)解:
去分母,得,
去括号,得:,
移项、合并同类项得,
检验,当时,,故是该方程的增根.
故此分式方程无解.
20.(1);
(2)
;
(3).
21.(1)设乙队单独施工x天完成全部工程,
∵甲队单独施工完成全部工程的天数是(天),
∴,
解得,,
经检验,是所列方程的根,且符合题意,
故乙队单独施工30天完成全部工程;
(2)设甲、乙两队工作一天的劳务费分别为m元、n元,
∴,
解得,,
故甲、乙两队工作一天的劳务费分别为3000元、10000元;
(3)设甲队单独施工a天,乙队单独施工b天,
则
∵,
∴,
∴,
∴,
∵,且,
∴
∴在总劳务费不超过28万元的情况下,则最快70天能完成总工程.
故答案为:70.
22.(1)①方法1:图2中阴影部分是边长为,因此面积为,
方法2:图2阴影部分也可以看作从边长为的正方形减去4个长为,宽为的长方形面积,因此有;
故答案为:,
(2)∵,,,
∵,,即,,
∴.
(3)1张1号,2张2号,3张3号卡片的总面积为,
而1张1号,2张2号,3张3号卡片可以拼成长为,宽为的长方形,
∴.
故答案为:.
23.(1)∵DE是的平分线,
∴
∵,
∴
∴
(2)过点E作交DA于点H,
∴
∵,
∴
∴,
∵,
∴,
∵,
∴
(3)解:∵平分,
∴,
设,则,
∴,
,,
∵,
∴
∵,
∴,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴
∵,
∴,
∴,
∴.
一.选择题(共10小题,满分30分,每小题3分)
1.在,,,,这五个数中,无理数的个数为( )
A.2 B.3 C.4 D.5
2.下列计算不正确的是( )
A. B.
C. D.
3.如图,在中,,,点在上,,将线段沿着方向平移得到线段,点,分别落在,边上,则的周长为( )
A. B. C. D.
4.已知关于的分式方程的解为整数,则符合条件的整数可以是( )
A.1 B.2 C.3 D.5
5.若关于x的不等式组有且仅有四个整数解,且关于y的一元一次方程的解为正整数,则符合条件的所有整数m的和为( )
A.-2 B.5 C.9 D.10
6.如图,,,则α、β、γ的关系是( )
B.
C. D.
7.一块麦田m亩,甲收割完这块麦田需n小时,乙比甲少用0.5小时就能收割完这块麦田,两人一起收割完这块麦田需要的时间是( )
A. B. C. D.
8.对于实数p,我们规定:用表示不小于的最小整数.例如:,,现在对72进行如下操作:72 ,即对72只需进行3次操作后变为2.类比上述操作:对512只需进行( )次操作后变为2.
A.3 B.4 C.5 D.6
9.的三边分别为a,b,c,且满足,则的形状为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
10.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EFHC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①ADBC;②GK平分∠AGC;③∠DGH=37°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题,满分18分,每小题3分)
11.已知.
(1)x的值为_____;
(2)x的算术平方根为_____.
12.已知关于x的不等式组的所有整数解的和为,m的取值范围是_________ .
13.若,且,则的值是_________.
14.一个角的两边分别与另一个角的两边垂直,且其中一个角为50°,则另一个角的度数是______________.
15.如图,,BC平分,设为,点E是射线BC上的一个动点,若,则的度数为__________.(用含的代数式表示).
16.若是完全平方式,则的值为______.
三.解答题(共7小题,满分52分)
17.(6分)解不等式(组)
(1) (2)
18.(6分)(1)计算:;
(2)分解因式:.
19.(8分)(1)先化简,在求值:,再从、0、1三个数中选择一个你认为合适的数作为的值代入求值,
(2)解方程:
20.(8分)因式分解:
(1); (2); (3)
21.(8分)两个工程队共同参与一项筑路工程,甲队单独施工30天完成总工程的,这时增加了乙队,两队又共同工作了15天,完成全部工程.
(1)求乙队单独施工多少天完成全部工程?
(2)若甲队工作4天,乙队工作3天共需支付工程劳务费42000元,甲队工作5天,乙队工作6天共需支付工程劳务费75000元,求甲、乙两队工作一天的劳务费分别为多少元?
(3)在(2)的条件下,若两个工程队不同时施工,在总劳务费不超过28万元的情况下,则最快______天能完成总工程.
22.(8分)有足够多的长方形和正方形卡片(如图1),分别记为1号,2号,3号卡片.
(1)如果选取4张3号卡片,拼成如图2所示的一个正方形,请用2种不同的方法表示阴影部分的面积(用含,的式子表示).
方法1:__________________________________________________.
方法2:__________________________________________________.
(2)若,求的值.
(3)如图3,选取1张1号卡片,2张2号卡片,3张3号卡片,可拼成一个长方形(无缝隙不重叠),根技图形的面积关系,因式分解:______.
23.已知,平分交射线于点,.
(1)如图1,求证:;
(2)如图2,点是射线上一点,过点作交射线于点,点是上一点,连接,求证:;
(3)如图3,在(2)的条件下,连接,点为延长线上一点,平分交于点,若平分,,,求的度数.
答案解析
选择题
1.A
【分析】根据无理数的定义判断即可.
【详解】解:在,,,,这五个数中,无理数有、共2个.
故选A.
2.C
【分析】根据同底数幂乘除法、合并同类项、积的乘方以及幂的乘方进行计算即可.
【详解】解:A、,原式计算正确,不符合题意;
B、,原式计算正确,不符合题意;
C、,原式计算错误,符合题意;
D、,原式计算正确,不符合题意;
故选:C.
3.C
【分析】根据平移的性质得到线段之间的等量关系,然后将的每条边长度分别求出计算即可.
【详解】解: ,
,
由平移可知:,,
,
,
,
,
,
,
的周长.
故选C
4.B
【分析】解该分式方程得,结合该分式方程的解为整数和分式有意义的条件,即得出为2的倍数且,即选B.
【详解】解:,
方程两边同时乘,得:,
解得:,
∵该分式方程的解为整数,
∴为2的倍数,
∴为2的倍数.
∵,
∴,
∴,
∴,
综上可知为2的倍数且.
∴只有B选项符合题意.
故选B.
5.B
【分析】表示出不等式组的解集,由不等式组有且只有4个整数解确定的取值范围,再由方程的解为正整数,求出满足条件的整数m,从而求解;
【详解】解:由
得:,
由不等式组有且仅有4个整数解,得到
,
解得:,
即整数,
解方程,
得:
因为关于y的一元一次方程的解为正整数
所以,
故整数m的和为5,
故选择:B
6.C
【分析】过点C、D分别作的平行线、,利用平行线的性质即可解决问题.
【详解】解:如图,过点C、D分别作的平行线、,
∵,
∴,
∴,,,
∵,,
∴,
∴.
故选:C.
7.A
【分析】先得到乙收割完这块麦田需要的时间,根据工作总量÷工作时间=工作效率,分别求出甲、乙的工作效率,再用工作总量÷甲、乙的工作效率和求出两人一起收割完这块麦田需要的工作时间.
【详解】乙收割完这块麦田需要的时间是 小时,
甲的工作效率是(亩/小时),
乙的工作效率 (亩/小时),
故两人一起收割完这块麦田需要的工作时间为 小时,
答:两人一起收割完这块麦田需要 小时.
故选A.
8.B
【分析】仿照题目已知的例题即可解答.
【详解】解:由题意得:
512 ,
∴对512只需进行4次操作后变为2;
故选:B.
9.B
【分析】先将a2﹣b2+ac﹣bc进行因式分解,可得a﹣b=0,进一步即可判断△ABC的形状.
【详解】解:∵a2﹣b2+ac﹣bc
=(a+b)(a﹣b)+c(a﹣b)
=(a+b+c)(a﹣b)=0,
∵a+b+c>0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形,
故选:B.
10.B
【分析】根据平行线的判定定理得到AD∥BC,故①正确;由平行线的性质得到∠AGK=∠CKG,等量代换得到∠AGK=∠CGK,求得GK平分∠AGC;故②正确;根据题意列方程得到∠FGA=∠DGH=37°,故③正确;设∠AGM=α,∠MGK=β,得到∠AGK=α+β,根据角平分线的定义即可得到结论.
【详解】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
∵∠FGA的余角比∠DGH大16°,
∴90°-∠FGA -∠DGH=16°,
∵∠FGA=∠DGH,
∴90°-2∠FGA=16°,
∴∠FGA=∠DGH=37°,故③正确;
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二.填空题
11.
【分析】(1)利用立方根的定义求得x的值;
(2)利用算术平方根的定义解答即可.
【详解】解:(1)∵,
∴,
∴x=3,
故答案为:3;
(2)由(1)知x=3,
3的算术平方根为,
故答案为:.
12.或
【分析】先求出不等式组的解集,然后根据不等式组的整数解的情况得到不等式组的整数解可以为、或、、、、、0、1、2、3,据此求解即可解答.
【详解】,
解不等式①得:,
解不等式②得:,
不等式组的解集为:,
不等式组的所有整数解的和为,
不等式组的整数解可以为、或、、、、、0、1、2、3,
或,
或,
故答案为:或.
13.
【分析】已知等式变形后,代入原式计算即可得到结果.
【详解】解∶,且,
,
原式.
故答案为∶.
14.50°或130°
【分析】此题可以通过两个图形得出这两个角的关系相等或互补.
【详解】如图:
图1中,根据垂直的量相等的角都等于90°,对顶角相等,
∴∠1=∠2=50°,
图2中,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,∴∠1+∠2=360°-90°-90°=180°.
∴∠2=130°
故答案为:50°或130°.
15.或
【分析】根据题意可分两种情况,①若点运动到上方,根据平行线的性质由可计算出的度数,再根据角平分线的性质和平行线的性质,计算出的度数,再由,,列出等量关系求解即可得出结论;②若点运动到下方,根据平行线的性质由可计算出的度数,再根据角平分线的性质和平行线的性质,计算出的度数,再由,列出等量关系求解即可得出结论.
【详解】解:如图,若点E运动到l1上方,
,
,
平分,
,
,
又,
,
,
解得;
如图,若点E运动到l1下方,
,
,
平分,
,
,
又,
,
,
解得.
综上的度数为或.
故答案为:或.
16.或
【分析】根据完全平方公式的特点:首平方,尾平方,首尾两数积的两倍在中央求解即可.
【详解】解:∵是完全平方式,
∴,
整理得:或,
解得或,
故答案为:或.
三.解答题
17.(1)解:移项合并同类项得,
,
系数化为1得,
,
∴不等式解集为;
(2)解:解不等式①得,
,
解不等式②得,
,
∴不等式组解集为:.
18.(1)原式
.
(2)原式
.
19.(1)解:原式
,
要使分式有意义,不能取,1,
则当时,原式.
(2)解:
去分母,得,
去括号,得:,
移项、合并同类项得,
检验,当时,,故是该方程的增根.
故此分式方程无解.
20.(1);
(2)
;
(3).
21.(1)设乙队单独施工x天完成全部工程,
∵甲队单独施工完成全部工程的天数是(天),
∴,
解得,,
经检验,是所列方程的根,且符合题意,
故乙队单独施工30天完成全部工程;
(2)设甲、乙两队工作一天的劳务费分别为m元、n元,
∴,
解得,,
故甲、乙两队工作一天的劳务费分别为3000元、10000元;
(3)设甲队单独施工a天,乙队单独施工b天,
则
∵,
∴,
∴,
∴,
∵,且,
∴
∴在总劳务费不超过28万元的情况下,则最快70天能完成总工程.
故答案为:70.
22.(1)①方法1:图2中阴影部分是边长为,因此面积为,
方法2:图2阴影部分也可以看作从边长为的正方形减去4个长为,宽为的长方形面积,因此有;
故答案为:,
(2)∵,,,
∵,,即,,
∴.
(3)1张1号,2张2号,3张3号卡片的总面积为,
而1张1号,2张2号,3张3号卡片可以拼成长为,宽为的长方形,
∴.
故答案为:.
23.(1)∵DE是的平分线,
∴
∵,
∴
∴
(2)过点E作交DA于点H,
∴
∵,
∴
∴,
∵,
∴,
∵,
∴
(3)解:∵平分,
∴,
设,则,
∴,
,,
∵,
∴
∵,
∴,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴
∵,
∴,
∴,
∴.
同课章节目录
