第29章 投影与视图 单元测试卷(无答案)2023—2024学年人教版数学九年级下册
文档属性
| 名称 | 第29章 投影与视图 单元测试卷(无答案)2023—2024学年人教版数学九年级下册 | 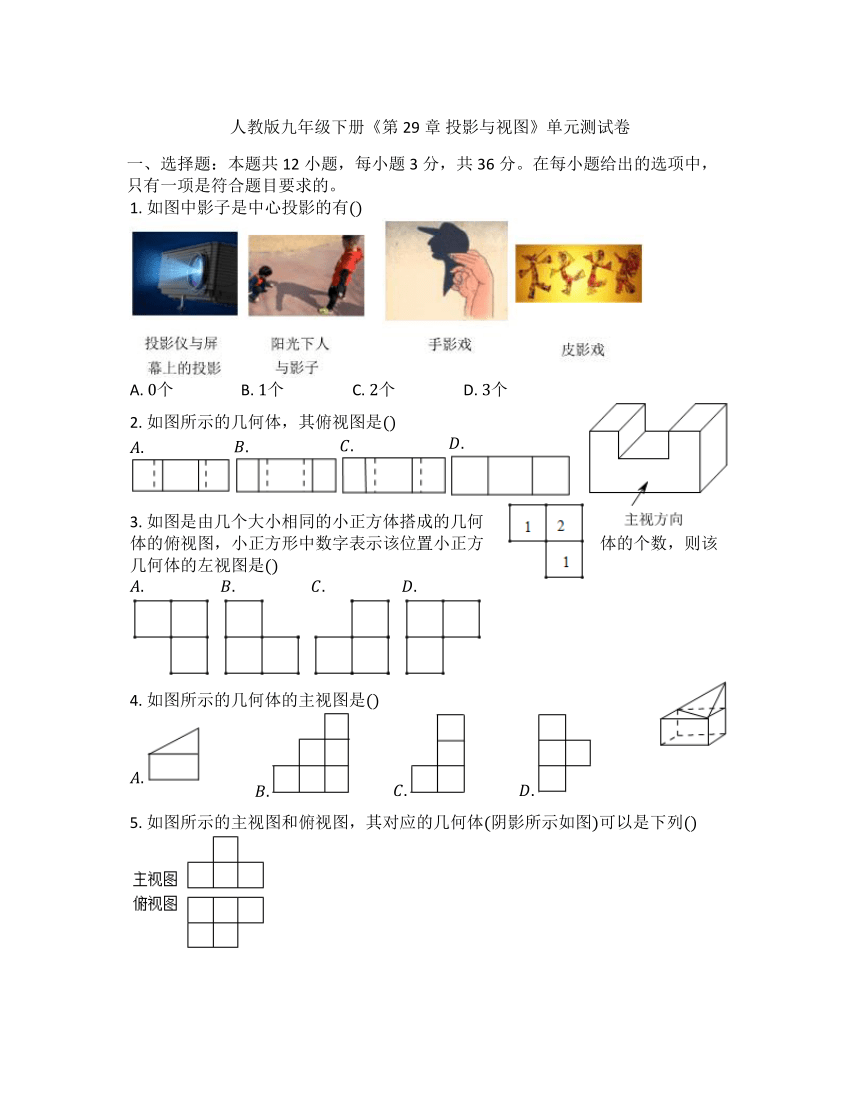 | |
| 格式 | docx | ||
| 文件大小 | 226.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 13:33:05 | ||
图片预览


文档简介
人教版九年级下册《第29章 投影与视图》单元测试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1. 如图中影子是中心投影的有
A. 个 B. 个 C. 个 D. 个
2. 如图所示的几何体,其俯视图是
3. 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是
4. 如图所示的几何体的主视图是
5. 如图所示的主视图和俯视图,其对应的几何体阴影所示如图可以是下列
6. 如果用表示个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么图中由个立方体叠成的几何体的主视图是
7. 上午九时,阳光灿烂,小李在地面上同时摆弄两根长度不相等的竹竿,若它们的影子长度相等,则这两根竹竿的相对位置可能是
A. 两根都垂直于地面 B. 两根都倒在地面上
C. 两根不平行斜竖在地面上 D. 两根平行斜竖在地面上
8. 某几何体的三视图如图所示,则下列说法错误的是
A. 该几何体是长方体 B. 该几何体的高是
C. 底面有一边的长是 D. 该几何体的表面积为平方单位
9. 如图所示,王华晚上由路灯下的处走到处时,测得影子的长为米,继续往前走米到达处时,测得影子的长为米,已知王华的身高是米,那么路灯的高度等于
A. 米 B. 米 C. 米 D. 米
10. 我们常用“随的增大而增大或减小”来表示两个变量之间的变化关系有这样一个情境:如图所示,小王从点沿直线经过路灯的正下方走到点,他在路灯下的影长随他与点之间的距离的变化而变化则下列函数中与之间的变化关系,最有可能与上述情境类似的是
A. B. C. D.
11. 如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是
A. B. C. D.
12. 图和图中所有的正方形都全等,将图的正方形放在图中的①②③④某一位置,所组成的图形不能围成正方体的位置是
A. ① B. ② C. ③ D. ④
二、填空题:本题共6小题,每小题3分,共18分。
13. 下列几何体中,仅主视图与左视图相同的是 ______ 填序号
14. 如图是某个几何体的三视图,该几何体是 ______ .
15. 图是一个小正方体的表面展开图,小正方形从图所示的位置依次翻到第格、第格、第格,这时小正方体朝上一面的字是______.
16. 如图,电灯在横杆的正上方,在灯光下的影子为,,,,点到的距离为,则与间的距离是__________
17. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的所有侧面积之和为______。
18. 用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是______个.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19. 如图所示,快下降到地面的某伞兵在灯光下的影子为试确定灯源的位置,并画出竖立在地面上木桩的影子保留作图痕迹,不要求写作法
画出图实物的三视图.
20. 如图是由一些棱长都为的小正方体组合成的简单几何体.该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
21. 请根据物体的三视图描述物体的形状.
要给物体的表面涂上防腐材料,根据图中的数据计算要涂上防腐材料的面积.
22. 如图,在水平地面上竖立着一面墙,墙外有一盏路灯光线恰好通过墙的最高点,且与地面形成角.墙在灯光下的影子为线段,并测得米.
求墙的高度结果精确到米;参考数据:,,
如果要缩短影子的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
23. 某兴趣小组开展课外活动.如图,,两地相距米,小明从点出发沿方向匀速前进,秒后到达点,此时他在某一灯光下的影长为,继续按原速行走秒到达点,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为米,然后他将速度提高到原来的倍,再行走秒到达点,此时他在同一灯光下的影长为点,,在一条直线上
请在图中画出光源点的位置,并画出他位于点时在这个灯光下的影长不写画法;
求小明原来的速度.
24. 如图,平面内的两条直线,,点、在直线上,点、在直线上,过、两点分别作直线的垂线,垂足分别为,,我们把线段叫做线段在直线上的正投影,其长度可记作,或,特别地线段在直线上的正投影就是线段,请依据上述定义解决如下问题:
如图,在锐角中,,,则______;
如图,在中,,,,求的面积;
如图,在钝角中,,点在边上,,,,求
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
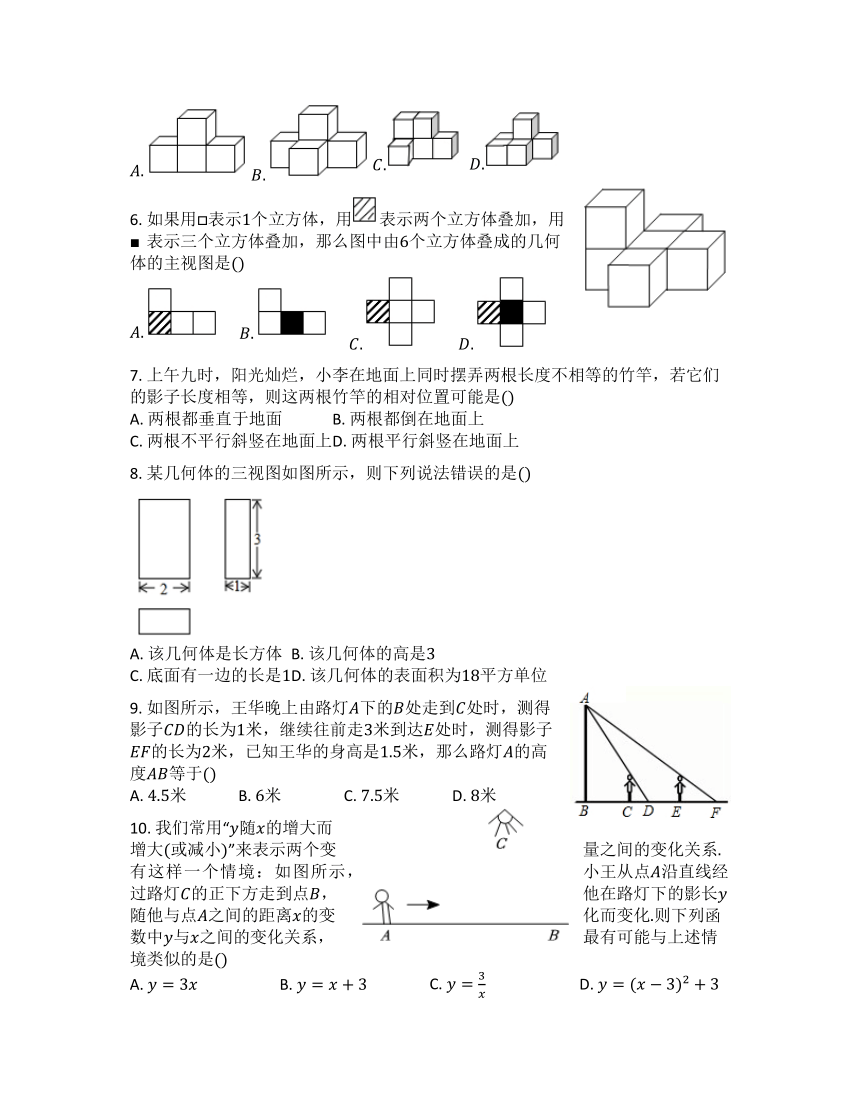
1. 如图中影子是中心投影的有
A. 个 B. 个 C. 个 D. 个
2. 如图所示的几何体,其俯视图是
3. 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是
4. 如图所示的几何体的主视图是
5. 如图所示的主视图和俯视图,其对应的几何体阴影所示如图可以是下列
6. 如果用表示个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么图中由个立方体叠成的几何体的主视图是
7. 上午九时,阳光灿烂,小李在地面上同时摆弄两根长度不相等的竹竿,若它们的影子长度相等,则这两根竹竿的相对位置可能是
A. 两根都垂直于地面 B. 两根都倒在地面上
C. 两根不平行斜竖在地面上 D. 两根平行斜竖在地面上
8. 某几何体的三视图如图所示,则下列说法错误的是
A. 该几何体是长方体 B. 该几何体的高是
C. 底面有一边的长是 D. 该几何体的表面积为平方单位
9. 如图所示,王华晚上由路灯下的处走到处时,测得影子的长为米,继续往前走米到达处时,测得影子的长为米,已知王华的身高是米,那么路灯的高度等于
A. 米 B. 米 C. 米 D. 米
10. 我们常用“随的增大而增大或减小”来表示两个变量之间的变化关系有这样一个情境:如图所示,小王从点沿直线经过路灯的正下方走到点,他在路灯下的影长随他与点之间的距离的变化而变化则下列函数中与之间的变化关系,最有可能与上述情境类似的是
A. B. C. D.
11. 如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是
A. B. C. D.
12. 图和图中所有的正方形都全等,将图的正方形放在图中的①②③④某一位置,所组成的图形不能围成正方体的位置是
A. ① B. ② C. ③ D. ④
二、填空题:本题共6小题,每小题3分,共18分。
13. 下列几何体中,仅主视图与左视图相同的是 ______ 填序号
14. 如图是某个几何体的三视图,该几何体是 ______ .
15. 图是一个小正方体的表面展开图,小正方形从图所示的位置依次翻到第格、第格、第格,这时小正方体朝上一面的字是______.
16. 如图,电灯在横杆的正上方,在灯光下的影子为,,,,点到的距离为,则与间的距离是__________
17. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的所有侧面积之和为______。
18. 用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是______个.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19. 如图所示,快下降到地面的某伞兵在灯光下的影子为试确定灯源的位置,并画出竖立在地面上木桩的影子保留作图痕迹,不要求写作法
画出图实物的三视图.
20. 如图是由一些棱长都为的小正方体组合成的简单几何体.该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
21. 请根据物体的三视图描述物体的形状.
要给物体的表面涂上防腐材料,根据图中的数据计算要涂上防腐材料的面积.
22. 如图,在水平地面上竖立着一面墙,墙外有一盏路灯光线恰好通过墙的最高点,且与地面形成角.墙在灯光下的影子为线段,并测得米.
求墙的高度结果精确到米;参考数据:,,
如果要缩短影子的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
23. 某兴趣小组开展课外活动.如图,,两地相距米,小明从点出发沿方向匀速前进,秒后到达点,此时他在某一灯光下的影长为,继续按原速行走秒到达点,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为米,然后他将速度提高到原来的倍,再行走秒到达点,此时他在同一灯光下的影长为点,,在一条直线上
请在图中画出光源点的位置,并画出他位于点时在这个灯光下的影长不写画法;
求小明原来的速度.
24. 如图,平面内的两条直线,,点、在直线上,点、在直线上,过、两点分别作直线的垂线,垂足分别为,,我们把线段叫做线段在直线上的正投影,其长度可记作,或,特别地线段在直线上的正投影就是线段,请依据上述定义解决如下问题:
如图,在锐角中,,,则______;
如图,在中,,,,求的面积;
如图,在钝角中,,点在边上,,,,求
