【沪科版八上同步练习】 期末数学试卷一(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 期末数学试卷一(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 14.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 10:39:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】 期末试卷一
一、单选题
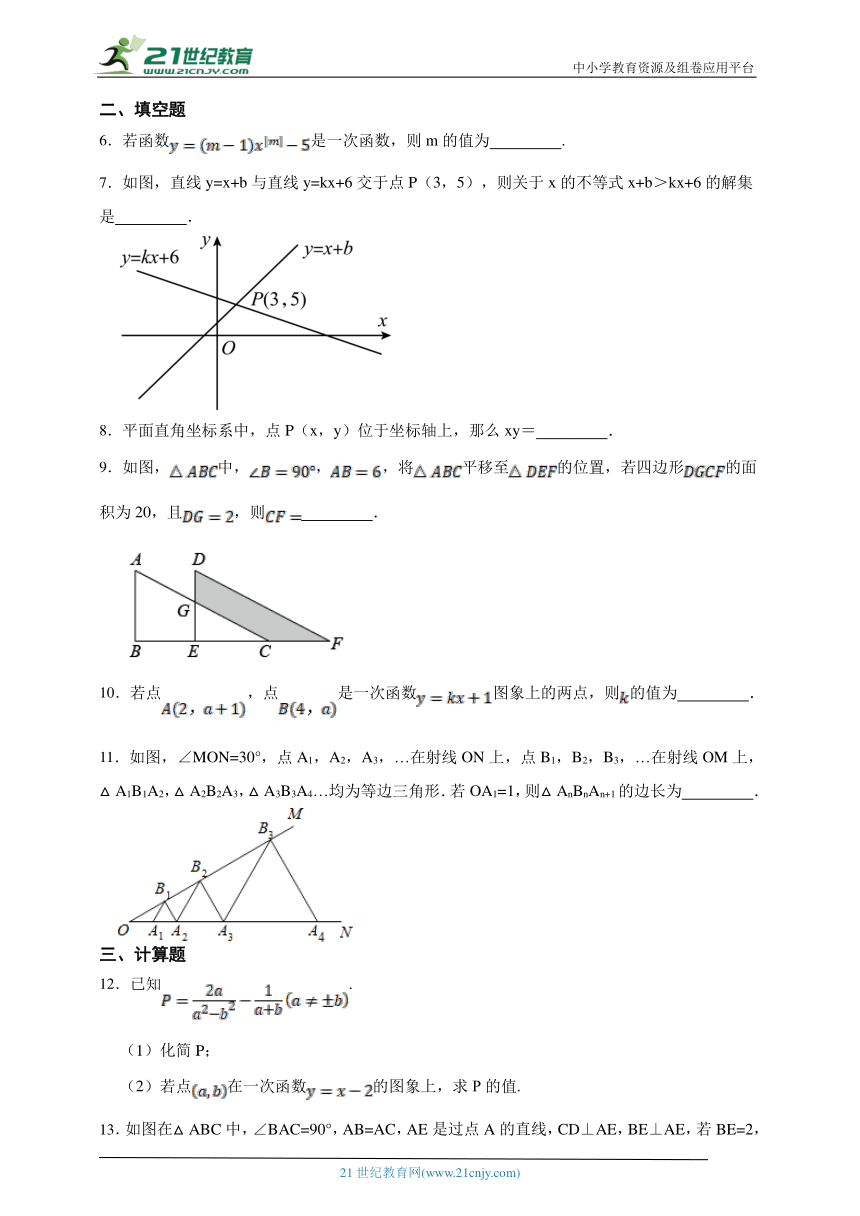
1.与直线y=﹣4x+2平行的直线是( )
A.y=4x+2 B.y=﹣4x+3 C.y D.y
2.如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
3.如图,在平面直角坐标系中,的顶点都在格点上,如果将沿轴翻折,得到,那么点的对应点的坐标为( )
A. B. C. D.
4.如图,已知AB=DC,∠ABC=∠DCB,能直接判定△ABC≌△DCB 的方法是( )
A.SAS B.AAS C.SSS D.ASA
5.已知一个等腰三角形两内角的度数之比为:,则这个等腰三角形的底角的度数为( )
A. B.或 C. D.或
二、填空题
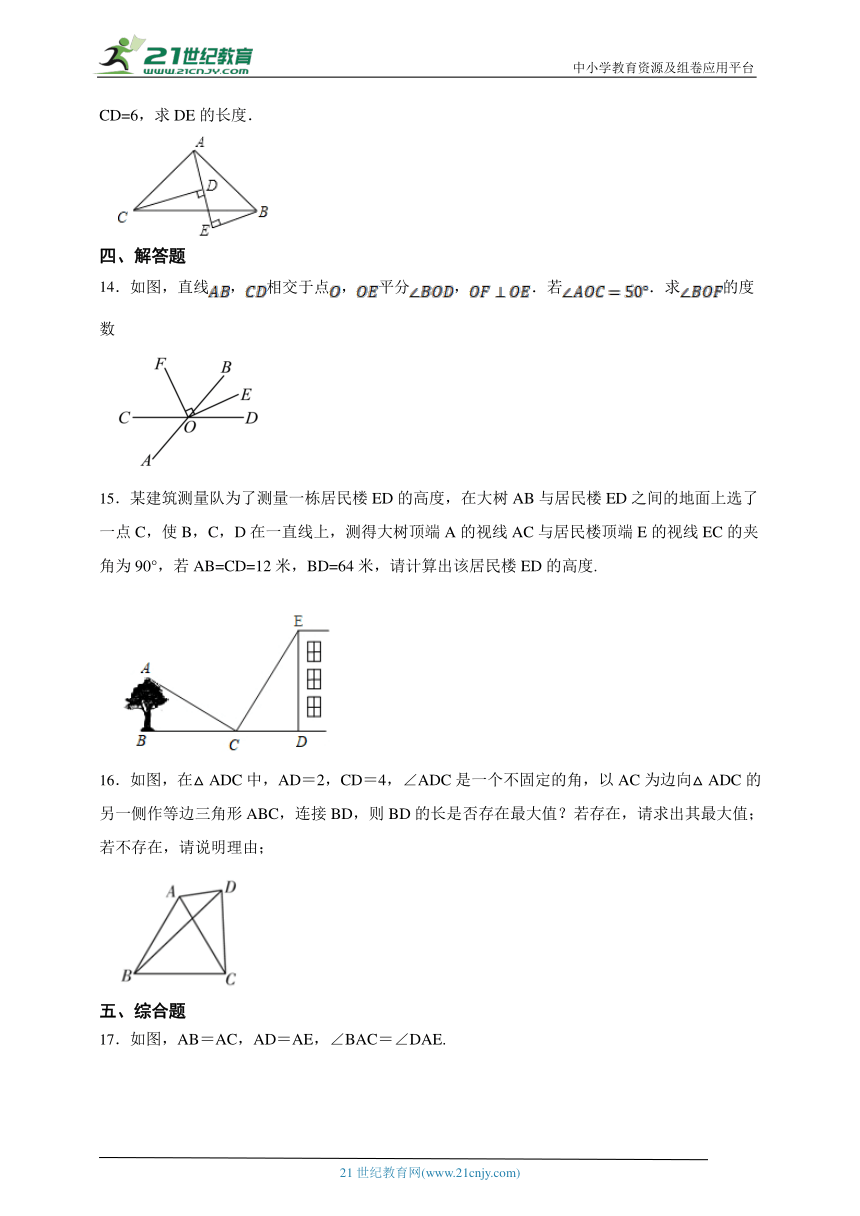
6.若函数是一次函数,则m的值为 .
7.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
8.平面直角坐标系中,点P(x,y)位于坐标轴上,那么xy= .
9.如图,中,,,将平移至的位置,若四边形的面积为20,且,则 .
10.若点,点是一次函数图象上的两点,则的值为 .
11.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
三、计算题
12.已知.
(1)化简P;
(2)若点在一次函数的图象上,求Р的值.
13.如图在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,CD⊥AE,BE⊥AE,若BE=2,CD=6,求DE的长度.
四、解答题
14.如图,直线,相交于点,平分,.若.求的度数
15.某建筑测量队为了测量一栋居民楼ED的高度,在大树AB与居民楼ED之间的地面上选了一点C,使B,C,D在一直线上,测得大树顶端A的视线AC与居民楼顶端E的视线EC的夹角为90°,若AB=CD=12米,BD=64米,请计算出该居民楼ED的高度.
16.如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
五、综合题
17.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
18.如图,以的边、分别向外作等腰直角与等腰直角,,连接和相交于点,交于点,交于点.
(1)试说明:≌;
(2)试说明:;
(3)试说明:点到边,所在直线的距离相等.
19.某移动公司推出A,B两种电话计费方式.
计费方式 月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
A 免费
B 免费
(1)设一个月内用移动电话主叫时间为tmin,根据上表,分别写出在不同时间范围内,方式A,方式B的计费金额关于t的函数解析式;
(2)若你预计每月主叫时间为350min,你将选择A,B哪种计费方式,并说明理由;
(3)请你根据月主叫时间t的不同范围,直接写出最省钱的计费方式.
六、实践探究题
20.【问题提出】
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后、我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在和中,,,,然后,对进行分类,可分为“是直角、钝角、锐角”三种情况进行探究.
【逐步探究】
(1)第一种情况:当是直角时,如图①,根据 定理,可得;
(2)第二种情况:当是钝角时,仍成立,请你完成证明.
已知:如图②,在和中,,,∠B=∠E,且,都是钝角,求证;
(3)第三种情况:当是锐角时,和不一定全等.在和中,,,,且,都是锐角,请你用尺规在图③中作出,使和不全等(不写作法,保留作图痕迹):
(4)【深入思考】
在和中,,,,且,都是锐角,若 时,则.
答案解析部分
1.【答案】B
【知识点】两一次函数图象相交或平行问题
2.【答案】A
【知识点】平行线的性质;翻折变换(折叠问题)
3.【答案】B
【知识点】关于坐标轴对称的点的坐标特征
4.【答案】A
【知识点】三角形全等的判定-SAS
5.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质
6.【答案】-1
【知识点】一次函数的概念
7.【答案】x>3
【知识点】一次函数与不等式(组)的关系
8.【答案】0
【知识点】点的坐标
9.【答案】4
【知识点】平移的性质
10.【答案】
【知识点】一次函数的性质
11.【答案】2n﹣1
【知识点】等边三角形的性质
12.【答案】(1)
(2)
【知识点】分式的化简求值;一次函数的概念
13.【答案】解:∵CD⊥AE,BE⊥AE,
∴∠CDA=∠AEB=∠BAC=90°,
∴∠ACD+∠CAD=∠BAE+∠CAD,
∴∠ACD=∠BAE,
在△ACD和△BAE中
∴△ACD≌△BAE(AAS),
∴AE=CD=6,AD=BE=2,
∴DE=AE﹣AD=6﹣2=4
【知识点】全等三角形的判定与性质;等腰直角三角形
14.【答案】
【知识点】垂线的概念;角平分线的性质;对顶角及其性质
15.【答案】解:由题意可知: ,
,
,
,
,
在 和 中,
,
≌ ,
,
又 CD=12米,BD=64米,
米,
米,
答:该居民楼ED的高度为52米.
【知识点】三角形全等的判定-AAS
16.【答案】证明:BD存在最大值;
如图,以AD为边做作等边三角形ADE,连接CE,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE=DE=2,∠BAC=∠EAD=60°,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠EAD+∠DAC
∴∠BAD=∠EAC,且AB=AC,AD=AE
∴△ABD≌△ACE
∴BD=CE
若点E,点D,点C不在一条直线上,则EC若点E,点D,点C在一条直线上,则EC=ED+DC.
∴EC≤ED+CD=2+4=6
∴BD≤6,
∴BD存在最大值,最大值是6.
【知识点】全等三角形的判定与性质;等边三角形的性质
17.【答案】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS)
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
【知识点】全等三角形的判定与性质
18.【答案】(1)解:,
,
,
与是等腰直角三角形,
,,
在和中,
,
≌
(2)解:,
,
由知,≌,
,
,
,
(3)解:≌,
,的面积的面积,
点到边,所在直线的距离相等.
【知识点】等腰三角形的性质;三角形全等的判定-SAS
19.【答案】(1)解:根据题意,设两种计费金额分别为、
当时,方式A的计费金额为元,方式B的计费金额为108元;
方式A的计费金额,方式B的计费金额为108元;
当时,方式A的计费金额为,方式B的计费金额为
总结如下表:
主叫时间/分钟 方式A计费() 方式B计费()
78 108
108
(2)解:当时,
,故选方式B计费.
(3)令,有解得
∴当时,方式A更省钱;
当时,方式A和B金额一样;
当时,方式B更省钱.
【知识点】一次函数的实际应用
20.【答案】(1)HL
(2)证明:如图②,过点C作交AB的延长线于点G,过点F作交DE的延长线于点H.
,
,
即.
在和中,
.
.
在和中,
.
.
在和中,
.
(3)解:作图如图③所示.
;
≥.
(4)≥∠A或∠B+∠C=90°
【知识点】三角形全等的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】 期末试卷一
一、单选题
1.与直线y=﹣4x+2平行的直线是( )
A.y=4x+2 B.y=﹣4x+3 C.y D.y
2.如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
3.如图,在平面直角坐标系中,的顶点都在格点上,如果将沿轴翻折,得到,那么点的对应点的坐标为( )
A. B. C. D.
4.如图,已知AB=DC,∠ABC=∠DCB,能直接判定△ABC≌△DCB 的方法是( )
A.SAS B.AAS C.SSS D.ASA
5.已知一个等腰三角形两内角的度数之比为:,则这个等腰三角形的底角的度数为( )
A. B.或 C. D.或
二、填空题
6.若函数是一次函数,则m的值为 .
7.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
8.平面直角坐标系中,点P(x,y)位于坐标轴上,那么xy= .
9.如图,中,,,将平移至的位置,若四边形的面积为20,且,则 .
10.若点,点是一次函数图象上的两点,则的值为 .
11.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
三、计算题
12.已知.
(1)化简P;
(2)若点在一次函数的图象上,求Р的值.
13.如图在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,CD⊥AE,BE⊥AE,若BE=2,CD=6,求DE的长度.
四、解答题
14.如图,直线,相交于点,平分,.若.求的度数
15.某建筑测量队为了测量一栋居民楼ED的高度,在大树AB与居民楼ED之间的地面上选了一点C,使B,C,D在一直线上,测得大树顶端A的视线AC与居民楼顶端E的视线EC的夹角为90°,若AB=CD=12米,BD=64米,请计算出该居民楼ED的高度.
16.如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
五、综合题
17.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
18.如图,以的边、分别向外作等腰直角与等腰直角,,连接和相交于点,交于点,交于点.
(1)试说明:≌;
(2)试说明:;
(3)试说明:点到边,所在直线的距离相等.
19.某移动公司推出A,B两种电话计费方式.
计费方式 月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
A 免费
B 免费
(1)设一个月内用移动电话主叫时间为tmin,根据上表,分别写出在不同时间范围内,方式A,方式B的计费金额关于t的函数解析式;
(2)若你预计每月主叫时间为350min,你将选择A,B哪种计费方式,并说明理由;
(3)请你根据月主叫时间t的不同范围,直接写出最省钱的计费方式.
六、实践探究题
20.【问题提出】
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后、我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在和中,,,,然后,对进行分类,可分为“是直角、钝角、锐角”三种情况进行探究.
【逐步探究】
(1)第一种情况:当是直角时,如图①,根据 定理,可得;
(2)第二种情况:当是钝角时,仍成立,请你完成证明.
已知:如图②,在和中,,,∠B=∠E,且,都是钝角,求证;
(3)第三种情况:当是锐角时,和不一定全等.在和中,,,,且,都是锐角,请你用尺规在图③中作出,使和不全等(不写作法,保留作图痕迹):
(4)【深入思考】
在和中,,,,且,都是锐角,若 时,则.
答案解析部分
1.【答案】B
【知识点】两一次函数图象相交或平行问题
2.【答案】A
【知识点】平行线的性质;翻折变换(折叠问题)
3.【答案】B
【知识点】关于坐标轴对称的点的坐标特征
4.【答案】A
【知识点】三角形全等的判定-SAS
5.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质
6.【答案】-1
【知识点】一次函数的概念
7.【答案】x>3
【知识点】一次函数与不等式(组)的关系
8.【答案】0
【知识点】点的坐标
9.【答案】4
【知识点】平移的性质
10.【答案】
【知识点】一次函数的性质
11.【答案】2n﹣1
【知识点】等边三角形的性质
12.【答案】(1)
(2)
【知识点】分式的化简求值;一次函数的概念
13.【答案】解:∵CD⊥AE,BE⊥AE,
∴∠CDA=∠AEB=∠BAC=90°,
∴∠ACD+∠CAD=∠BAE+∠CAD,
∴∠ACD=∠BAE,
在△ACD和△BAE中
∴△ACD≌△BAE(AAS),
∴AE=CD=6,AD=BE=2,
∴DE=AE﹣AD=6﹣2=4
【知识点】全等三角形的判定与性质;等腰直角三角形
14.【答案】
【知识点】垂线的概念;角平分线的性质;对顶角及其性质
15.【答案】解:由题意可知: ,
,
,
,
,
在 和 中,
,
≌ ,
,
又 CD=12米,BD=64米,
米,
米,
答:该居民楼ED的高度为52米.
【知识点】三角形全等的判定-AAS
16.【答案】证明:BD存在最大值;
如图,以AD为边做作等边三角形ADE,连接CE,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE=DE=2,∠BAC=∠EAD=60°,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠EAD+∠DAC
∴∠BAD=∠EAC,且AB=AC,AD=AE
∴△ABD≌△ACE
∴BD=CE
若点E,点D,点C不在一条直线上,则EC
∴EC≤ED+CD=2+4=6
∴BD≤6,
∴BD存在最大值,最大值是6.
【知识点】全等三角形的判定与性质;等边三角形的性质
17.【答案】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS)
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
【知识点】全等三角形的判定与性质
18.【答案】(1)解:,
,
,
与是等腰直角三角形,
,,
在和中,
,
≌
(2)解:,
,
由知,≌,
,
,
,
(3)解:≌,
,的面积的面积,
点到边,所在直线的距离相等.
【知识点】等腰三角形的性质;三角形全等的判定-SAS
19.【答案】(1)解:根据题意,设两种计费金额分别为、
当时,方式A的计费金额为元,方式B的计费金额为108元;
方式A的计费金额,方式B的计费金额为108元;
当时,方式A的计费金额为,方式B的计费金额为
总结如下表:
主叫时间/分钟 方式A计费() 方式B计费()
78 108
108
(2)解:当时,
,故选方式B计费.
(3)令,有解得
∴当时,方式A更省钱;
当时,方式A和B金额一样;
当时,方式B更省钱.
【知识点】一次函数的实际应用
20.【答案】(1)HL
(2)证明:如图②,过点C作交AB的延长线于点G,过点F作交DE的延长线于点H.
,
,
即.
在和中,
.
.
在和中,
.
.
在和中,
.
(3)解:作图如图③所示.
;
≥.
(4)≥∠A或∠B+∠C=90°
【知识点】三角形全等的判定
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
