【沪科版九上同步练习】 21.2 二次函数的图像和性质(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 21.2 二次函数的图像和性质(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
21.2二次函数的图像和性质
一、填空题
1.抛物线y=x2-6的顶点坐标是 .
2.将抛物线 先沿水平方向向右平移1个单位,再沿竖直方向向上平移3个单位,则得到的新抛物线的解析式为 .
3.抛物线y=ax2 经过点(3,5),则 的值等于 .
4.抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-15.已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是 .
6.如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是 .
二、单选题
7.二次函数y=ax2+bx+c的图像如图,正确的是( )
A.a>0 B.b<0 C.c<0 D.a+b+c<0
8.抛物线y=ax2+bx+c(a≠0)过(2,8)和(﹣6,8)两点,则此抛物线的对称轴为( )
A.直线x=0 B.直线x=1 C.直线x=﹣2 D.直线x=﹣1
9.抛物线y=3x2向左平移4个单位,再向下平移2个单位,所得到的抛物线是( )
A.y=3(x﹣4)2+2 B.y=3(x﹣4)2﹣2
C.y=3(x+4)2﹣2 D.y=3(x+4)2+2
10.抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
A.b2﹣4ac<0 B.abc<0 C. D.a﹣b+c<0
11.将抛物线先向左平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为( )
A. B.
C. D.
三、解答题
12.已知二次函数的图像经过,,求抛物线的解析式
13. 目前,云南省有130多种水果资源,约占全国的.第十六届亚洲果蔬产业博览会是中国领先的水果产业链贸易盛会,此次博览会,云南出产的苹果、蓝莓、冰糖橙、甜柿、草莓、石榴等品种深受全国经销商们青睐.某果园今年种植的草莓喜获丰收,采摘上市15天全部售罄,该果园果农对销售情况进行统计后发现,在该草莓上市第x天时,日销售量P(单位:千克)与之间的函数关系为,草莓单价y(单位:元/千克)与x之间的函数关系如图所示.
(1)当时,求y与x之间的函数关系式;
(2)设日销售额为W元,当时,求W的最大值.
14.如图①,在平面直角坐标系xOy中.抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点B在点A右侧),AB=4,与y轴交于点C.直线y=-x+2经过点B,C.
(1)求抛物线的解析式;
(2)如图②,点P为BC上方抛物线上一点,过点P作PE∥x轴交直线BC于点E,作PF∥y轴交直线BC于点F,求△PEF周长的最大值;
(3)在(2)的条件下,若点S是x轴上的动点,点Q为平面内一点,是否存在点S,Q,使得以S,Q,E,F为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
四、计算题
15.已知
(1)化简T.
(2)若a为二次函数的最小值,求此时的T值.
16.已知抛物线的顶点为(2,3),且经过点(3,1),求此抛物线对应的函数解析式。
五、综合题
17.如图为二次函数 图象的一部分,它与轴的一个交点坐标为A ,与 轴的交点坐标为B .
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
18.如图,二次函数 的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足 ≤kx+b的x的取值范围.
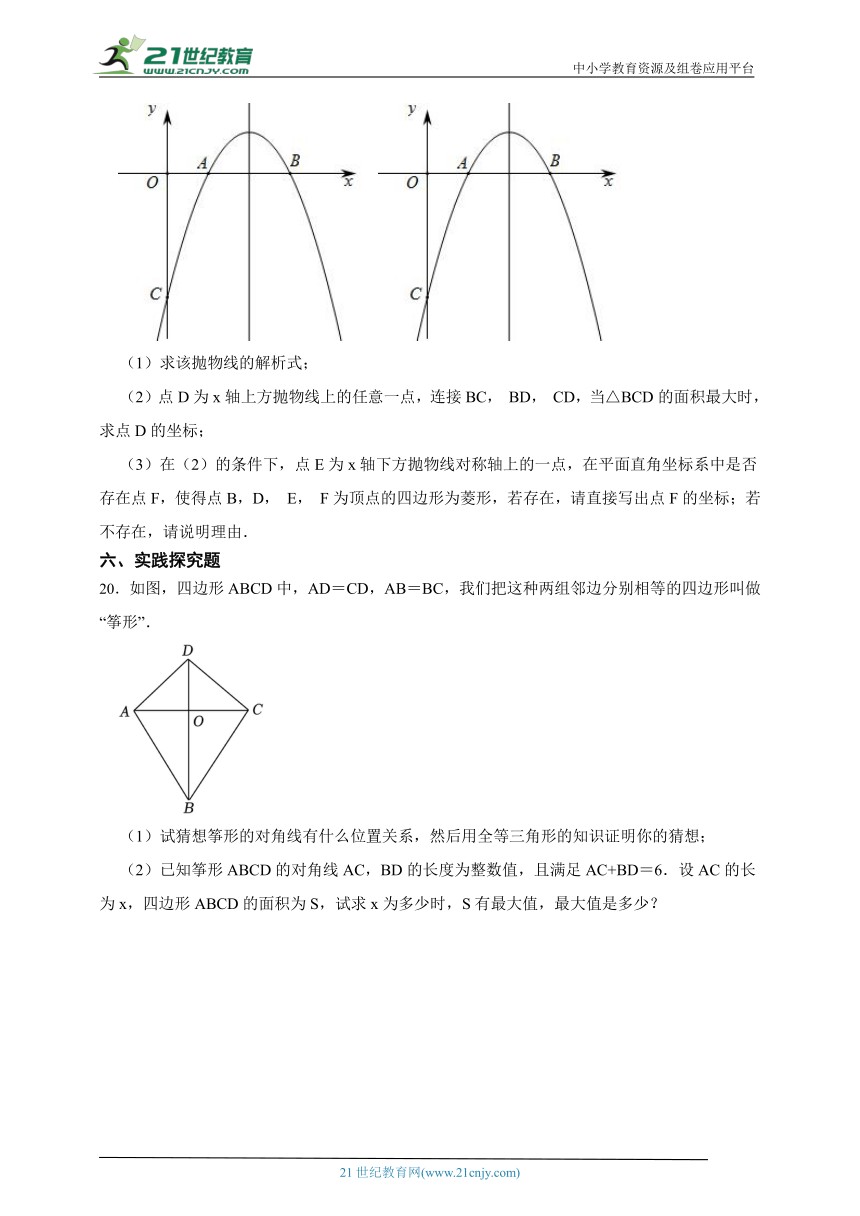
19.如图,在平面直角坐标系中,抛物线 与x轴交于 和 ,与y轴交于点C.
(1)求该抛物线的解析式;
(2)点D为x轴上方抛物线上的任意一点,连接BC, BD, CD,当△BCD的面积最大时,求点D的坐标;
(3)在(2)的条件下,点E为x轴下方抛物线对称轴上的一点,在平面直角坐标系中是否存在点F,使得点B,D, E, F为顶点的四边形为菱形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
六、实践探究题
20.如图,四边形ABCD中,AD=CD,AB=BC,我们把这种两组邻边分别相等的四边形叫做“筝形”.
(1)试猜想筝形的对角线有什么位置关系,然后用全等三角形的知识证明你的猜想;
(2)已知筝形ABCD的对角线AC,BD的长度为整数值,且满足AC+BD=6.设AC的长为x,四边形ABCD的面积为S,试求x为多少时,S有最大值,最大值是多少?
答案解析部分
1.【答案】(0,-6)
【知识点】二次函数图象上点的坐标特征
2.【答案】 或
【知识点】二次函数图象的几何变换
3.【答案】
【知识点】二次函数图象上点的坐标特征
4.【答案】2≤t<11
【知识点】二次函数与一次函数的综合应用
5.【答案】m>﹣
【知识点】三角形三边关系;二次函数图象上点的坐标特征
6.【答案】①④⑤
【知识点】二次函数的最值;正方形的性质;三角形全等的判定-SAS
7.【答案】D
【知识点】二次函数图象与系数的关系
8.【答案】C
【知识点】二次函数图象上点的坐标特征
9.【答案】C
【知识点】二次函数图象的几何变换
10.【答案】C
【知识点】二次函数图象与系数的关系
11.【答案】C
【知识点】二次函数图象的几何变换
12.【答案】解:把(-1,0)、(3,0)代入中
得,
解得,
∴二次函数的解析式为.
【知识点】待定系数法求二次函数解析式
13.【答案】(1)解:由题意,当时,;
当时,设函数解析式为,
又图象过,,
∴.
∴.
∴此时函数解析式为.
综上,当时,.
(2)解:由题意,结合(1)当时,单价为,
此时销量,
∴日销售额为.
当时,销量,单价为,
∴日销售额为
.
又,
∴当时,W随x的增大而增大.
∴当时,当时,W取最大值,最大值为800.
综上,当时,当时,W取最大值,最大值为800元.
【知识点】分段函数;二次函数的最值
14.【答案】(1)解:直线y=-x+2,令x=0得y=2,
令y=0得-x+2=0,解得x=3.
∴B(3,0),C(0,2),
∵AB=4,
∴A(-1,0),
将A(-1,0),B(3,0),C(0,2)代入y=ax2+bx+c得,
,解得,
∴抛物线的解析式为y=-x2+x+2;
(2)解:设点P(m,-m2+m+2),
∵PE∥x轴,
∴-m2+m+2=-xE+2,
∴xE=m2-2m,
∴E(m2-2m,-m2+m+2),
∵PF∥y轴,
∴F(m,-m+2),
∴PE=m-(m2-2m)=-m2+3m,
PF=-m2+m+2-(-m+2)=-m2+2m,
EF==|m2-3m|,
∵点P为BC上方抛物线上一点,
∴0<m<3,
∴EF=(3m-m2),
∴△PEF的周长=-m2+3m+(-m2+2m)+(3m-m2)=-(m-)2+,
∵-<0,
∴当m=时,△PEF周长的最大值为;
(3)解:存在,
由(2)知m=时,E(-,),F(,1),
∴EF==,
设S(s,0),
①线段EF为菱形的边,四边形EFQS为菱形时,如图,
∴ES=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EFQS为菱形,点F的坐标可由点E向右平移个单位长度,向下平移个单位长度得到,
∴点Q可由点S向右平移个单位长度,向下平移个单位长度得到,
∴Q(,-)或(,-);
②线段EF为菱形的边,四边形EQSF为菱形时,如图,
∴FS=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EQSF为菱形,点E的坐标可由点F向左平移个单位长度,向上平移个单位长度得到,
∴点Q可由点S向左平移个单位长度,向上平移个单位长度得到,
∴Q(,)或(,);
③线段EF为菱形的对角线,四边形EQFS为菱形时,如图,
∴ES=FS,
∴=,
∴s=-,
设Q(p,q),
∴p-=-+,解得p=,
q+0=+1,解得q=,
∴Q(-,).
综上所述,存在,点Q的坐标为(,-)或(,-)或(,)或(,)或(-,).
【知识点】二次函数的最值;二次函数与一次函数的综合应用;二次函数-动态几何问题
15.【答案】(1)
(2)
【知识点】分式的化简求值;二次函数的最值
16.【答案】解:设抛物线对应的函数解析式是y=a(x-2)2+3,
把(3,1)代入得ax(3-2)2+3=1,解得a=-2,
所以抛物线解析式为y=-2(x-2)2+3
【知识点】待定系数法求二次函数解析式
17.【答案】(1)解:∵抛物线经过 两点
解得
∴抛物线的解析式为
(2)解: 可化为
∴抛物线 的顶点坐标为
又∵此抛物线向左平移 个单位,再向下平移 个单位,
∴平移后的抛物线的顶点坐标为
∴平移后的抛物线的解析式为
二次函数 的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).
【知识点】待定系数法求二次函数解析式;坐标与图形变化﹣平移
18.【答案】(1)解:∵抛物线 经过点A(﹣2,0), ∴ . ∴∴抛物线解析式为y=x2+6x+8 ∴点C坐标(0,8). ∵对称轴x=﹣3,B、C关于对称轴对称, ∴点B坐标(﹣6,8) ∵y=kx+b经过点A、B, ∴ 解得 ∴一次函数解析式为y=﹣2x﹣4.
(2)解:由图象可知,满足 ≤kx+b的x的取值范围为﹣6≤x≤﹣2.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;二次函数与一次函数的综合应用
19.【答案】(1)解:∵抛物线经过点A(1,0),点B(3,0),
∴ , 解得: ,
∴抛物线的解析式为: ;
(2)解:存在,
过点D作DM y轴,交BC于点 M, 交x轴于点N,作CH⊥DM于点H,
∵点C是抛物线与y轴的交点,
∴点C的坐标为C(0,-3),
设BC的解析式为y=kx+b,
∵BC经过点B(3,0),点C(0,-3),
∴ ,
解得: ,
∴BC的解析式为: ,
设D的坐标为 (a, ),则M的坐标为M(a, )
∴
=
= DM + DM
= DM (CH+BN)
= DM OB
= ( ) 3
=
=
∴当a= 时,S最大= ,
∴D ( );
(3)存在,点F的坐标为 或 或
【知识点】待定系数法求二次函数解析式;二次函数-动态几何问题
20.【答案】(1)解:筝形的对角线相互垂直,理由如下:
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ADB=∠CDB,
∴AC⊥BD;
(2)解:∵AD=CD,∠ADB=∠CDB,
∴OA=OC,
∴S筝形ABCD=AC BD,
∵AC+BD=6,AC=x,
∴BD=6-x
将BD=6-x代入S筝形ABCD=AC BD,
得S筝形ABCD=AC BD=x(6-x)=-(x-3)2+≤,
∴当x=3时,S有最大值,最大值是.
【知识点】二次函数的最值;线段垂直平分线的判定;三角形全等的判定-SSS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
21.2二次函数的图像和性质
一、填空题
1.抛物线y=x2-6的顶点坐标是 .
2.将抛物线 先沿水平方向向右平移1个单位,再沿竖直方向向上平移3个单位,则得到的新抛物线的解析式为 .
3.抛物线y=ax2 经过点(3,5),则 的值等于 .
4.抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1
6.如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是 .
二、单选题
7.二次函数y=ax2+bx+c的图像如图,正确的是( )
A.a>0 B.b<0 C.c<0 D.a+b+c<0
8.抛物线y=ax2+bx+c(a≠0)过(2,8)和(﹣6,8)两点,则此抛物线的对称轴为( )
A.直线x=0 B.直线x=1 C.直线x=﹣2 D.直线x=﹣1
9.抛物线y=3x2向左平移4个单位,再向下平移2个单位,所得到的抛物线是( )
A.y=3(x﹣4)2+2 B.y=3(x﹣4)2﹣2
C.y=3(x+4)2﹣2 D.y=3(x+4)2+2
10.抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
A.b2﹣4ac<0 B.abc<0 C. D.a﹣b+c<0
11.将抛物线先向左平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为( )
A. B.
C. D.
三、解答题
12.已知二次函数的图像经过,,求抛物线的解析式
13. 目前,云南省有130多种水果资源,约占全国的.第十六届亚洲果蔬产业博览会是中国领先的水果产业链贸易盛会,此次博览会,云南出产的苹果、蓝莓、冰糖橙、甜柿、草莓、石榴等品种深受全国经销商们青睐.某果园今年种植的草莓喜获丰收,采摘上市15天全部售罄,该果园果农对销售情况进行统计后发现,在该草莓上市第x天时,日销售量P(单位:千克)与之间的函数关系为,草莓单价y(单位:元/千克)与x之间的函数关系如图所示.
(1)当时,求y与x之间的函数关系式;
(2)设日销售额为W元,当时,求W的最大值.
14.如图①,在平面直角坐标系xOy中.抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点B在点A右侧),AB=4,与y轴交于点C.直线y=-x+2经过点B,C.
(1)求抛物线的解析式;
(2)如图②,点P为BC上方抛物线上一点,过点P作PE∥x轴交直线BC于点E,作PF∥y轴交直线BC于点F,求△PEF周长的最大值;
(3)在(2)的条件下,若点S是x轴上的动点,点Q为平面内一点,是否存在点S,Q,使得以S,Q,E,F为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
四、计算题
15.已知
(1)化简T.
(2)若a为二次函数的最小值,求此时的T值.
16.已知抛物线的顶点为(2,3),且经过点(3,1),求此抛物线对应的函数解析式。
五、综合题
17.如图为二次函数 图象的一部分,它与轴的一个交点坐标为A ,与 轴的交点坐标为B .
(1)求这个二次函数的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
18.如图,二次函数 的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足 ≤kx+b的x的取值范围.
19.如图,在平面直角坐标系中,抛物线 与x轴交于 和 ,与y轴交于点C.
(1)求该抛物线的解析式;
(2)点D为x轴上方抛物线上的任意一点,连接BC, BD, CD,当△BCD的面积最大时,求点D的坐标;
(3)在(2)的条件下,点E为x轴下方抛物线对称轴上的一点,在平面直角坐标系中是否存在点F,使得点B,D, E, F为顶点的四边形为菱形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
六、实践探究题
20.如图,四边形ABCD中,AD=CD,AB=BC,我们把这种两组邻边分别相等的四边形叫做“筝形”.
(1)试猜想筝形的对角线有什么位置关系,然后用全等三角形的知识证明你的猜想;
(2)已知筝形ABCD的对角线AC,BD的长度为整数值,且满足AC+BD=6.设AC的长为x,四边形ABCD的面积为S,试求x为多少时,S有最大值,最大值是多少?
答案解析部分
1.【答案】(0,-6)
【知识点】二次函数图象上点的坐标特征
2.【答案】 或
【知识点】二次函数图象的几何变换
3.【答案】
【知识点】二次函数图象上点的坐标特征
4.【答案】2≤t<11
【知识点】二次函数与一次函数的综合应用
5.【答案】m>﹣
【知识点】三角形三边关系;二次函数图象上点的坐标特征
6.【答案】①④⑤
【知识点】二次函数的最值;正方形的性质;三角形全等的判定-SAS
7.【答案】D
【知识点】二次函数图象与系数的关系
8.【答案】C
【知识点】二次函数图象上点的坐标特征
9.【答案】C
【知识点】二次函数图象的几何变换
10.【答案】C
【知识点】二次函数图象与系数的关系
11.【答案】C
【知识点】二次函数图象的几何变换
12.【答案】解:把(-1,0)、(3,0)代入中
得,
解得,
∴二次函数的解析式为.
【知识点】待定系数法求二次函数解析式
13.【答案】(1)解:由题意,当时,;
当时,设函数解析式为,
又图象过,,
∴.
∴.
∴此时函数解析式为.
综上,当时,.
(2)解:由题意,结合(1)当时,单价为,
此时销量,
∴日销售额为.
当时,销量,单价为,
∴日销售额为
.
又,
∴当时,W随x的增大而增大.
∴当时,当时,W取最大值,最大值为800.
综上,当时,当时,W取最大值,最大值为800元.
【知识点】分段函数;二次函数的最值
14.【答案】(1)解:直线y=-x+2,令x=0得y=2,
令y=0得-x+2=0,解得x=3.
∴B(3,0),C(0,2),
∵AB=4,
∴A(-1,0),
将A(-1,0),B(3,0),C(0,2)代入y=ax2+bx+c得,
,解得,
∴抛物线的解析式为y=-x2+x+2;
(2)解:设点P(m,-m2+m+2),
∵PE∥x轴,
∴-m2+m+2=-xE+2,
∴xE=m2-2m,
∴E(m2-2m,-m2+m+2),
∵PF∥y轴,
∴F(m,-m+2),
∴PE=m-(m2-2m)=-m2+3m,
PF=-m2+m+2-(-m+2)=-m2+2m,
EF==|m2-3m|,
∵点P为BC上方抛物线上一点,
∴0<m<3,
∴EF=(3m-m2),
∴△PEF的周长=-m2+3m+(-m2+2m)+(3m-m2)=-(m-)2+,
∵-<0,
∴当m=时,△PEF周长的最大值为;
(3)解:存在,
由(2)知m=时,E(-,),F(,1),
∴EF==,
设S(s,0),
①线段EF为菱形的边,四边形EFQS为菱形时,如图,
∴ES=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EFQS为菱形,点F的坐标可由点E向右平移个单位长度,向下平移个单位长度得到,
∴点Q可由点S向右平移个单位长度,向下平移个单位长度得到,
∴Q(,-)或(,-);
②线段EF为菱形的边,四边形EQSF为菱形时,如图,
∴FS=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EQSF为菱形,点E的坐标可由点F向左平移个单位长度,向上平移个单位长度得到,
∴点Q可由点S向左平移个单位长度,向上平移个单位长度得到,
∴Q(,)或(,);
③线段EF为菱形的对角线,四边形EQFS为菱形时,如图,
∴ES=FS,
∴=,
∴s=-,
设Q(p,q),
∴p-=-+,解得p=,
q+0=+1,解得q=,
∴Q(-,).
综上所述,存在,点Q的坐标为(,-)或(,-)或(,)或(,)或(-,).
【知识点】二次函数的最值;二次函数与一次函数的综合应用;二次函数-动态几何问题
15.【答案】(1)
(2)
【知识点】分式的化简求值;二次函数的最值
16.【答案】解:设抛物线对应的函数解析式是y=a(x-2)2+3,
把(3,1)代入得ax(3-2)2+3=1,解得a=-2,
所以抛物线解析式为y=-2(x-2)2+3
【知识点】待定系数法求二次函数解析式
17.【答案】(1)解:∵抛物线经过 两点
解得
∴抛物线的解析式为
(2)解: 可化为
∴抛物线 的顶点坐标为
又∵此抛物线向左平移 个单位,再向下平移 个单位,
∴平移后的抛物线的顶点坐标为
∴平移后的抛物线的解析式为
二次函数 的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).
【知识点】待定系数法求二次函数解析式;坐标与图形变化﹣平移
18.【答案】(1)解:∵抛物线 经过点A(﹣2,0), ∴ . ∴∴抛物线解析式为y=x2+6x+8 ∴点C坐标(0,8). ∵对称轴x=﹣3,B、C关于对称轴对称, ∴点B坐标(﹣6,8) ∵y=kx+b经过点A、B, ∴ 解得 ∴一次函数解析式为y=﹣2x﹣4.
(2)解:由图象可知,满足 ≤kx+b的x的取值范围为﹣6≤x≤﹣2.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;二次函数与一次函数的综合应用
19.【答案】(1)解:∵抛物线经过点A(1,0),点B(3,0),
∴ , 解得: ,
∴抛物线的解析式为: ;
(2)解:存在,
过点D作DM y轴,交BC于点 M, 交x轴于点N,作CH⊥DM于点H,
∵点C是抛物线与y轴的交点,
∴点C的坐标为C(0,-3),
设BC的解析式为y=kx+b,
∵BC经过点B(3,0),点C(0,-3),
∴ ,
解得: ,
∴BC的解析式为: ,
设D的坐标为 (a, ),则M的坐标为M(a, )
∴
=
= DM + DM
= DM (CH+BN)
= DM OB
= ( ) 3
=
=
∴当a= 时,S最大= ,
∴D ( );
(3)存在,点F的坐标为 或 或
【知识点】待定系数法求二次函数解析式;二次函数-动态几何问题
20.【答案】(1)解:筝形的对角线相互垂直,理由如下:
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ADB=∠CDB,
∴AC⊥BD;
(2)解:∵AD=CD,∠ADB=∠CDB,
∴OA=OC,
∴S筝形ABCD=AC BD,
∵AC+BD=6,AC=x,
∴BD=6-x
将BD=6-x代入S筝形ABCD=AC BD,
得S筝形ABCD=AC BD=x(6-x)=-(x-3)2+≤,
∴当x=3时,S有最大值,最大值是.
【知识点】二次函数的最值;线段垂直平分线的判定;三角形全等的判定-SSS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
