【沪科版九上同步练习】 21.4 二次函数的应用(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 21.4 二次函数的应用(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 13.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
21.4二次函数的应用
一、单选题
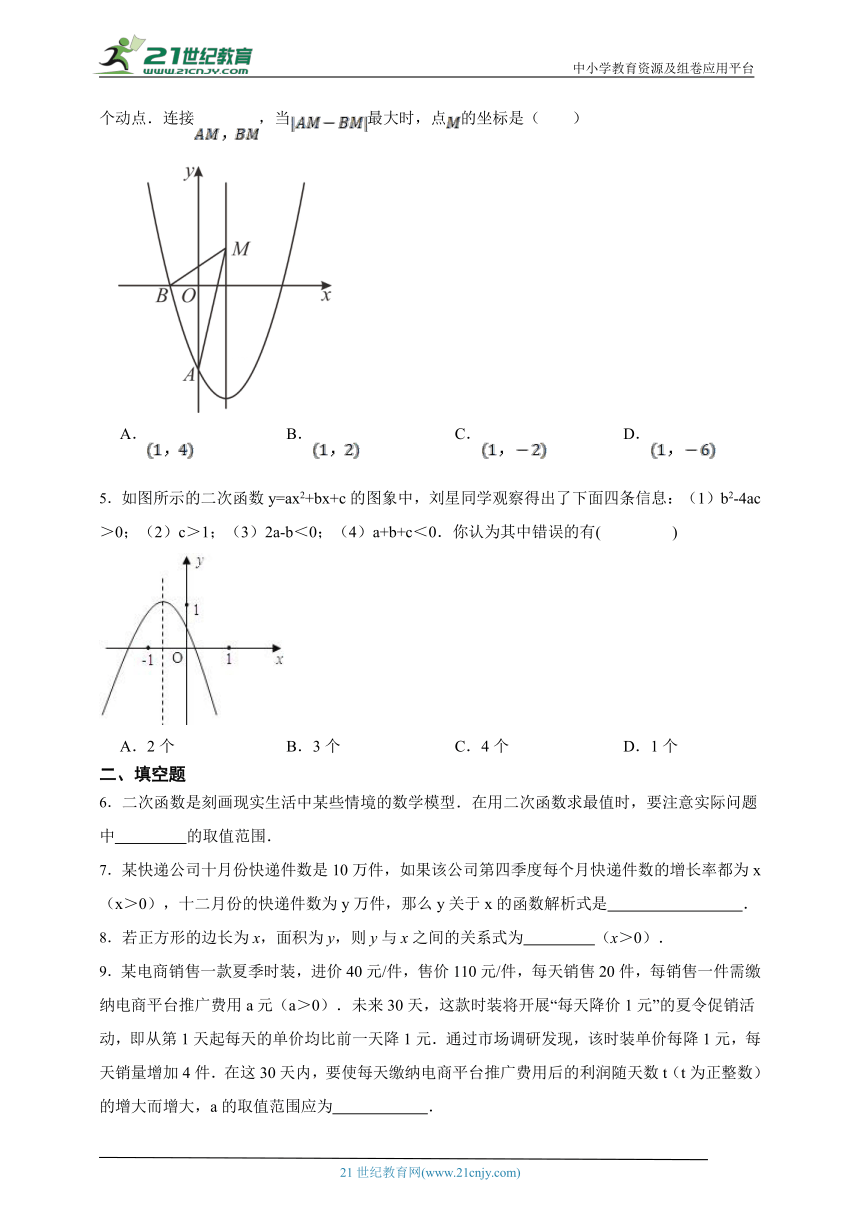
1.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系(为常数,).有下列结论:
①值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
2.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 ( )
A. B. C. D.
3.某广场有一喷水池,水从地面喷出.如图所示,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:)的一部分,则水喷出的最大高度是( )。
A. B. C. D.
4.如图,抛物线与轴交于点,与轴的负半轴交于点,点是对称轴上的一个动点.连接,当最大时,点的坐标是( )
A. B. C. D.
5.如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
A.2个 B.3个 C.4个 D.1个
二、填空题
6.二次函数是刻画现实生活中某些情境的数学模型.在用二次函数求最值时,要注意实际问题中 的取值范围.
7.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
8.若正方形的边长为x,面积为y,则y与x之间的关系式为 (x>0).
9.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
10.某校九年级数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤40,且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40
售价(元/件) x+35
每天销量(件) 150-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为w元.则w与x的函数表达式为 。
11.在抛物线上,过轴上点作两条相互垂直的直线与抛物线分别交于,,,,且,分别是线段,的中点,面积的最小值为 .
三、计算题
12.图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点O处,石块从投石机竖直方向上的点C处被投出,已知石块运动轨迹所在抛物线的顶点坐标是,.
(1)求抛物线的表达式;
(2)在斜坡上的点A建有垂直于水平线的城墙,且,,,点D,A,B在一条直线上.通过计算说明石块能否飞越城墙.
13.如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
14. 如图,在中,.点P从点A出发,以的速度沿运动;同时,点Q从点B出发,以的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设动点运动的时间为.
(1)试写出的面积与之间的函数表达式;
(2)当t为何值时,的面积最大 最大面积是多少
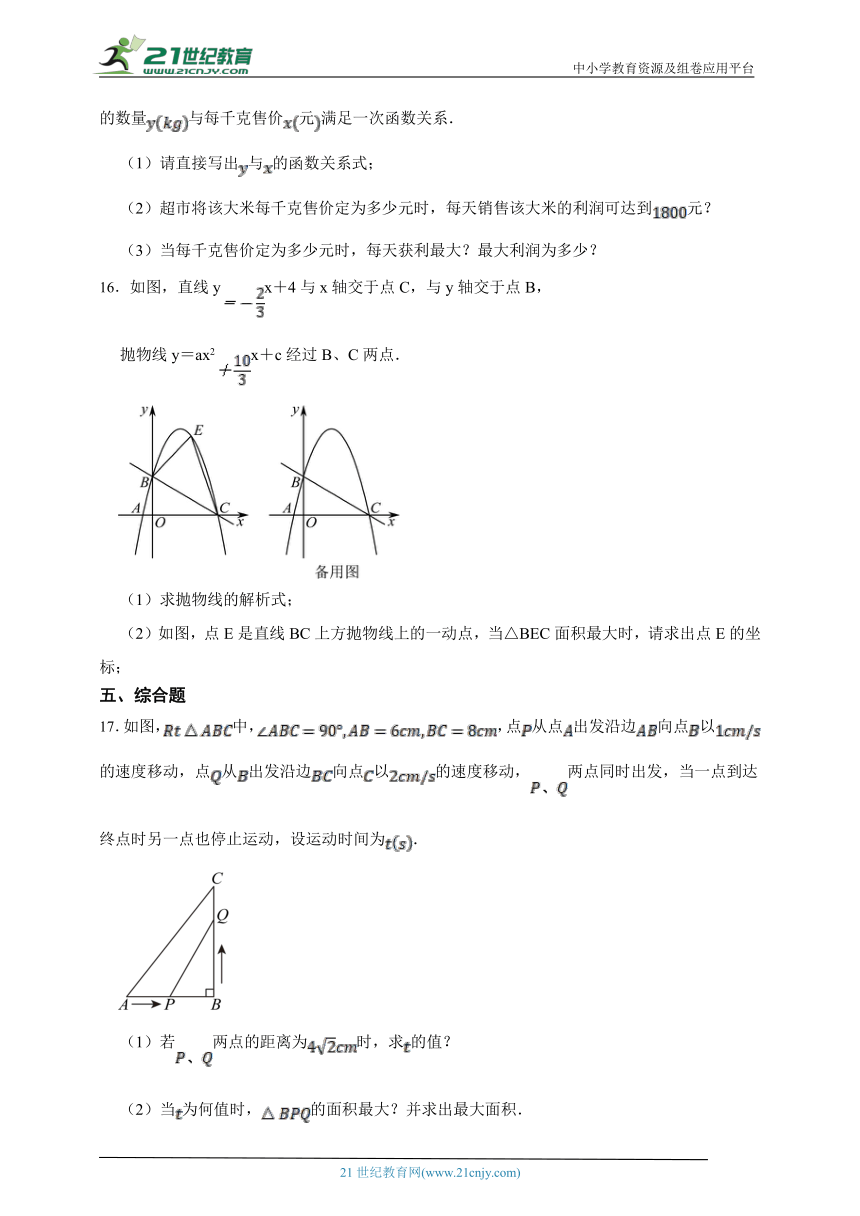
15.某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克元的该大米,以不低于成本价且不超过每千克元的价格销售当每千克售价为元时,每天售出大米;当每千克售价为元时,每天售出大米,通过分析销售数据发现:每天销售大米的数量与每千克售价元满足一次函数关系.
(1)请直接写出与的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到元?
(3)当每千克售价定为多少元时,每天获利最大?最大利润为多少?
16.如图,直线yx+4与x轴交于点C,与y轴交于点B,
抛物线y=ax2x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
五、综合题
17.如图,中,,点从点出发沿边向点以的速度移动,点从出发沿边向点以的速度移动,两点同时出发,当一点到达终点时另一点也停止运动,设运动时间为.
(1)若两点的距离为时,求的值?
(2)当为何值时,的面积最大?并求出最大面积.
18.2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为每件40元,据市场分析,若按每件80元销售,一个月能售出100件;销售单价每降1元,月销售量就增加5件,针对这种玩具的销售情况,请解答以下问题:
(1)设每件玩具的售价为x元(x为正整数),每月的销售量为y件.直接写出y与x的函数关系式;
(2)设该商店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该商店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定吉祥物玩具的销售单价?
19.某厂按用户的月需求量x (件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本为y (万元),y与x的关系式为 (a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,1≤n≤12)的关系式为x=n2-13n+72,且得到了下表中的数据.
月份n(月) 1 2
成本y(万元/件) 11 12
(1)请直接写出a,b的值;
(2)设第n个月的利润为w(万元),请求出W与n的函数关系式,并求出这一年的12个月中,哪个月份的利润为84万元?
(3)在这一年的前8个月中,哪个月的利润最大?最大利润是多少?
六、实践探究题
20.某饭店特制了一批高脚杯,分为男士杯和女士杯(如图1),相关信息如下:
素材 内容
素材1 高脚杯:如图1,类似这种杯托上立着一只细长脚的杯子.从下往上分为三部分:杯托,杯脚,杯体.杯托为一个圆;水平放置时候,杯脚经过杯托圆心,并垂直任意直径;杯体的水平横截面都为圆,这些圆的圆心都在杯脚所在直线上.
素材2 图2坐标系中,特制男士杯可以看作线段AB,OC,抛物线DCE(实线部分),线段DF,线段EG绕y轴旋转形成的立体图形(不考虑杯子厚度,下同).图2坐标系中,特制女士杯可以看作线段AB,OC,抛物线FCG(虚线部分)绕y轴旋转形成的立体图形.
素材3 已知,图2坐标系中,OC=50mm,记为C(0,50),D(﹣25,75),E(25,75),F(﹣25,150),G(25,150).
根据以上素材内容,尝试求解以下问题:
(1)求抛物线DCE和抛物线FCG的解析式;
(2)当杯子水平放置及杯内液体(无泡沫)静止时,若男士杯中液体与女士杯中液体最深处深度均为30mm,求两者液体最上层表面圆面积相差多少?(结果保留π)
(3)当杯子水平放置及杯内液体(无泡沫)静止时,若男士杯中液体与女士杯中液体最深处深度相等,两者液体最上层表面圆面积相差450πmm2,求杯中液体最深度为多少?
答案解析部分
1.【答案】C
【知识点】二次函数的实际应用-抛球问题
2.【答案】C
【知识点】函数解析式;二次函数的实际应用-几何问题
3.【答案】A
【知识点】二次函数的实际应用-喷水问题
4.【答案】D
【知识点】轴对称的应用-最短距离问题;二次函数-动态几何问题
5.【答案】D
【知识点】二次函数-动态几何问题
6.【答案】自变量
【知识点】二次函数的其他应用
7.【答案】y=10(x+1)2
【知识点】二次函数的实际应用-百分率问题
8.【答案】y=x2
【知识点】二次函数的其他应用
9.【答案】0<a≤5
【知识点】二次函数的实际应用-销售问题
10.【答案】W=-2x2+140x+750
【知识点】二次函数的实际应用-销售问题
11.【答案】4
【知识点】二次函数-动态几何问题
12.【答案】(1)抛物线的表达式为y=
(2)石块不能飞越城墙
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
13.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
14.【答案】(1)解:由题意得:,
=;
即;
(2)解:∵,
∴当时,的面积最大,最大值是
【知识点】二次函数的最值;二次函数-动态几何问题
15.【答案】(1)解:根据题意设y=kx+b,
当每千克售价为5元时,每天售出大米950kg;
当每千克售价为6元时,每天售出大米900kg,
则,
解得:,
则y与x的函数关系式为;
(2)解:定价为x元,每千克利润(x-4)元,
由(1)知销售量为,
则,
解得:舍,,
超市将该大米每千克售价定为6元时,每天销售该大米的利润可达到1800元;
(3)解:设利润为W元,
根据题意可得:,
即,
,对称轴为,
当时,W随x的增大而增大,
又,
时,元
当每千克售价定为7元时,每天获利最大,最大利润为2550元.
【知识点】待定系数法求一次函数解析式;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
16.【答案】(1)解:当x=0时,y=4,
∴B(0,4),
当y=0时,x+4=0,
解得:x=6,
∴C(6,0),
把B(0,4)和C(6,0)代入抛物线y=ax2x+c中得:
,
解得:,
∴抛物线的解析式为:yx2x+4
(2)解:如图1,过E作EG∥y轴,交直线BC于G,
设E(m,m2m+4),则G(m,m+4),
∴EG=(m2m+4)﹣(m+4)4m,
∴S△BECEG OC6(4m)=﹣2(m﹣3)2+18,
∵﹣2<0,
∴S有最大值,此时E(3,8);
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数图象上点的坐标特征;二次函数的实际应用-几何问题
17.【答案】(1)或2
(2)当为时,的面积最大,最大面积为
【知识点】勾股定理;二次函数-动态几何问题
18.【答案】(1)解:设每件玩具的售价为x元,每月的销售量为y件,由题意得:,
即y与x的函数关系式为:;
(2)解:设该商店每月获得的利润为w元,由题意得:,
∴当售价为70元时,每月获得的利润最大,最大利润为4500元,80-70=10(元),答:当销售单价降低10元时,每月获得的利润最大,最大利润是4500元;
(3)解:由题意得:,
当时,解得:x=74或66,
∵-5<0,
∴二次函数的图象开口向下,
∴当时,,
∵要让消费者得到最大的实惠,
∴x=66,
答:吉祥物玩具的销售单价应定为66元一件.
【知识点】列一次函数关系式;二次函数的实际应用-销售问题
19.【答案】(1)解:当n=1时,x= n2-13n+72=1-13+72=60,即x=60,y=11,
当n=2时,x= n2-13n+72=4-26+72=50,即x=50,y=12,
把x=60,y=11和x=50,y=12分别代入 ,得
,解得: ,
所以a=6,b=300
(2)解:w=x(18-y)=x(18- )=12x-300 =12(n2-13n+72)-300=12n2-156n+564,
由w=84,得12n2-156n+564=84,
解得,n 1=5,n 2=8,
∴5月份和8月份的利润均为84万元
(3)解:由(2)可知,w=12(n -6.5)2+57 ,
∵12>0,
∴当1≤n≤6时,w随n的增大而减小,当n=1时,w最大为420,
当7≤n≤8时,w随n的增大而增大,当n=8时,w最大为84,
∵420>84,
∴在这一年的前8个月中,1月的利润最大,最大利润是420万元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
20.【答案】(1)∵C点为抛物线DCE和抛物线FCG的顶点,对称轴为y轴,
∴设抛物线DCE的解析式为:y=a1x2+50,抛物线FCG的解析式为:y=a2x2+50,
∵点D(﹣25,75)在抛物线DCE上,点F( 25,150)在抛物线FCG上,
∴75=(﹣25)2a1+50,150=252a2+50,
∴a1=,a2=,
∴抛物线DCE:y=x2+50;抛物线FCG:y=x2+50;
(2)设男士杯中液体与女士杯中液体最上层表面圆的半径分别为R,r,
在抛物线FCG中:当y=50+30=80时,x2+50=80,
∴x2===r2,
∵30﹣(75﹣50)=5>0,
则R=25,
∴πR2﹣πr2=(252﹣)π=437.5π(mm2);
(3)解:当50<y<75时,由抛物线解析式可得:R2=25(y﹣50),r2=(y﹣50 ),
∴πR2﹣πr2=450π,
即25(y﹣50)﹣(y﹣50)=450,
解得y=74;
则最深度为74﹣50=24(mm);
当y>75时,由图象可得:R2=252,r2=(y﹣50 ),
可列方程:πR2﹣πr2=450π,
则252﹣(y﹣50)=450,
解得y=78;
则最深度为78﹣50=28(mm).
综上:杯中液体最深度为24mm或28mm.
【知识点】二次函数的其他应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
21.4二次函数的应用
一、单选题
1.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系(为常数,).有下列结论:
①值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
2.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 ( )
A. B. C. D.
3.某广场有一喷水池,水从地面喷出.如图所示,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:)的一部分,则水喷出的最大高度是( )。
A. B. C. D.
4.如图,抛物线与轴交于点,与轴的负半轴交于点,点是对称轴上的一个动点.连接,当最大时,点的坐标是( )
A. B. C. D.
5.如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
A.2个 B.3个 C.4个 D.1个
二、填空题
6.二次函数是刻画现实生活中某些情境的数学模型.在用二次函数求最值时,要注意实际问题中 的取值范围.
7.某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .
8.若正方形的边长为x,面积为y,则y与x之间的关系式为 (x>0).
9.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
10.某校九年级数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤40,且x为正整数)的售价与销量的相关信息如下表:
时间(天) 1≤x≤40
售价(元/件) x+35
每天销量(件) 150-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为w元.则w与x的函数表达式为 。
11.在抛物线上,过轴上点作两条相互垂直的直线与抛物线分别交于,,,,且,分别是线段,的中点,面积的最小值为 .
三、计算题
12.图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点O处,石块从投石机竖直方向上的点C处被投出,已知石块运动轨迹所在抛物线的顶点坐标是,.
(1)求抛物线的表达式;
(2)在斜坡上的点A建有垂直于水平线的城墙,且,,,点D,A,B在一条直线上.通过计算说明石块能否飞越城墙.
13.如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
14. 如图,在中,.点P从点A出发,以的速度沿运动;同时,点Q从点B出发,以的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设动点运动的时间为.
(1)试写出的面积与之间的函数表达式;
(2)当t为何值时,的面积最大 最大面积是多少
15.某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克元的该大米,以不低于成本价且不超过每千克元的价格销售当每千克售价为元时,每天售出大米;当每千克售价为元时,每天售出大米,通过分析销售数据发现:每天销售大米的数量与每千克售价元满足一次函数关系.
(1)请直接写出与的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到元?
(3)当每千克售价定为多少元时,每天获利最大?最大利润为多少?
16.如图,直线yx+4与x轴交于点C,与y轴交于点B,
抛物线y=ax2x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
五、综合题
17.如图,中,,点从点出发沿边向点以的速度移动,点从出发沿边向点以的速度移动,两点同时出发,当一点到达终点时另一点也停止运动,设运动时间为.
(1)若两点的距离为时,求的值?
(2)当为何值时,的面积最大?并求出最大面积.
18.2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为每件40元,据市场分析,若按每件80元销售,一个月能售出100件;销售单价每降1元,月销售量就增加5件,针对这种玩具的销售情况,请解答以下问题:
(1)设每件玩具的售价为x元(x为正整数),每月的销售量为y件.直接写出y与x的函数关系式;
(2)设该商店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该商店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定吉祥物玩具的销售单价?
19.某厂按用户的月需求量x (件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本为y (万元),y与x的关系式为 (a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,1≤n≤12)的关系式为x=n2-13n+72,且得到了下表中的数据.
月份n(月) 1 2
成本y(万元/件) 11 12
(1)请直接写出a,b的值;
(2)设第n个月的利润为w(万元),请求出W与n的函数关系式,并求出这一年的12个月中,哪个月份的利润为84万元?
(3)在这一年的前8个月中,哪个月的利润最大?最大利润是多少?
六、实践探究题
20.某饭店特制了一批高脚杯,分为男士杯和女士杯(如图1),相关信息如下:
素材 内容
素材1 高脚杯:如图1,类似这种杯托上立着一只细长脚的杯子.从下往上分为三部分:杯托,杯脚,杯体.杯托为一个圆;水平放置时候,杯脚经过杯托圆心,并垂直任意直径;杯体的水平横截面都为圆,这些圆的圆心都在杯脚所在直线上.
素材2 图2坐标系中,特制男士杯可以看作线段AB,OC,抛物线DCE(实线部分),线段DF,线段EG绕y轴旋转形成的立体图形(不考虑杯子厚度,下同).图2坐标系中,特制女士杯可以看作线段AB,OC,抛物线FCG(虚线部分)绕y轴旋转形成的立体图形.
素材3 已知,图2坐标系中,OC=50mm,记为C(0,50),D(﹣25,75),E(25,75),F(﹣25,150),G(25,150).
根据以上素材内容,尝试求解以下问题:
(1)求抛物线DCE和抛物线FCG的解析式;
(2)当杯子水平放置及杯内液体(无泡沫)静止时,若男士杯中液体与女士杯中液体最深处深度均为30mm,求两者液体最上层表面圆面积相差多少?(结果保留π)
(3)当杯子水平放置及杯内液体(无泡沫)静止时,若男士杯中液体与女士杯中液体最深处深度相等,两者液体最上层表面圆面积相差450πmm2,求杯中液体最深度为多少?
答案解析部分
1.【答案】C
【知识点】二次函数的实际应用-抛球问题
2.【答案】C
【知识点】函数解析式;二次函数的实际应用-几何问题
3.【答案】A
【知识点】二次函数的实际应用-喷水问题
4.【答案】D
【知识点】轴对称的应用-最短距离问题;二次函数-动态几何问题
5.【答案】D
【知识点】二次函数-动态几何问题
6.【答案】自变量
【知识点】二次函数的其他应用
7.【答案】y=10(x+1)2
【知识点】二次函数的实际应用-百分率问题
8.【答案】y=x2
【知识点】二次函数的其他应用
9.【答案】0<a≤5
【知识点】二次函数的实际应用-销售问题
10.【答案】W=-2x2+140x+750
【知识点】二次函数的实际应用-销售问题
11.【答案】4
【知识点】二次函数-动态几何问题
12.【答案】(1)抛物线的表达式为y=
(2)石块不能飞越城墙
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
13.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
14.【答案】(1)解:由题意得:,
=;
即;
(2)解:∵,
∴当时,的面积最大,最大值是
【知识点】二次函数的最值;二次函数-动态几何问题
15.【答案】(1)解:根据题意设y=kx+b,
当每千克售价为5元时,每天售出大米950kg;
当每千克售价为6元时,每天售出大米900kg,
则,
解得:,
则y与x的函数关系式为;
(2)解:定价为x元,每千克利润(x-4)元,
由(1)知销售量为,
则,
解得:舍,,
超市将该大米每千克售价定为6元时,每天销售该大米的利润可达到1800元;
(3)解:设利润为W元,
根据题意可得:,
即,
,对称轴为,
当时,W随x的增大而增大,
又,
时,元
当每千克售价定为7元时,每天获利最大,最大利润为2550元.
【知识点】待定系数法求一次函数解析式;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
16.【答案】(1)解:当x=0时,y=4,
∴B(0,4),
当y=0时,x+4=0,
解得:x=6,
∴C(6,0),
把B(0,4)和C(6,0)代入抛物线y=ax2x+c中得:
,
解得:,
∴抛物线的解析式为:yx2x+4
(2)解:如图1,过E作EG∥y轴,交直线BC于G,
设E(m,m2m+4),则G(m,m+4),
∴EG=(m2m+4)﹣(m+4)4m,
∴S△BECEG OC6(4m)=﹣2(m﹣3)2+18,
∵﹣2<0,
∴S有最大值,此时E(3,8);
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数图象上点的坐标特征;二次函数的实际应用-几何问题
17.【答案】(1)或2
(2)当为时,的面积最大,最大面积为
【知识点】勾股定理;二次函数-动态几何问题
18.【答案】(1)解:设每件玩具的售价为x元,每月的销售量为y件,由题意得:,
即y与x的函数关系式为:;
(2)解:设该商店每月获得的利润为w元,由题意得:,
∴当售价为70元时,每月获得的利润最大,最大利润为4500元,80-70=10(元),答:当销售单价降低10元时,每月获得的利润最大,最大利润是4500元;
(3)解:由题意得:,
当时,解得:x=74或66,
∵-5<0,
∴二次函数的图象开口向下,
∴当时,,
∵要让消费者得到最大的实惠,
∴x=66,
答:吉祥物玩具的销售单价应定为66元一件.
【知识点】列一次函数关系式;二次函数的实际应用-销售问题
19.【答案】(1)解:当n=1时,x= n2-13n+72=1-13+72=60,即x=60,y=11,
当n=2时,x= n2-13n+72=4-26+72=50,即x=50,y=12,
把x=60,y=11和x=50,y=12分别代入 ,得
,解得: ,
所以a=6,b=300
(2)解:w=x(18-y)=x(18- )=12x-300 =12(n2-13n+72)-300=12n2-156n+564,
由w=84,得12n2-156n+564=84,
解得,n 1=5,n 2=8,
∴5月份和8月份的利润均为84万元
(3)解:由(2)可知,w=12(n -6.5)2+57 ,
∵12>0,
∴当1≤n≤6时,w随n的增大而减小,当n=1时,w最大为420,
当7≤n≤8时,w随n的增大而增大,当n=8时,w最大为84,
∵420>84,
∴在这一年的前8个月中,1月的利润最大,最大利润是420万元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
20.【答案】(1)∵C点为抛物线DCE和抛物线FCG的顶点,对称轴为y轴,
∴设抛物线DCE的解析式为:y=a1x2+50,抛物线FCG的解析式为:y=a2x2+50,
∵点D(﹣25,75)在抛物线DCE上,点F( 25,150)在抛物线FCG上,
∴75=(﹣25)2a1+50,150=252a2+50,
∴a1=,a2=,
∴抛物线DCE:y=x2+50;抛物线FCG:y=x2+50;
(2)设男士杯中液体与女士杯中液体最上层表面圆的半径分别为R,r,
在抛物线FCG中:当y=50+30=80时,x2+50=80,
∴x2===r2,
∵30﹣(75﹣50)=5>0,
则R=25,
∴πR2﹣πr2=(252﹣)π=437.5π(mm2);
(3)解:当50<y<75时,由抛物线解析式可得:R2=25(y﹣50),r2=(y﹣50 ),
∴πR2﹣πr2=450π,
即25(y﹣50)﹣(y﹣50)=450,
解得y=74;
则最深度为74﹣50=24(mm);
当y>75时,由图象可得:R2=252,r2=(y﹣50 ),
可列方程:πR2﹣πr2=450π,
则252﹣(y﹣50)=450,
解得y=78;
则最深度为78﹣50=28(mm).
综上:杯中液体最深度为24mm或28mm.
【知识点】二次函数的其他应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
