第三章 位置与坐标 学情评估卷(含答案)北师大版数学八年级上册
文档属性
| 名称 | 第三章 位置与坐标 学情评估卷(含答案)北师大版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 295.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-21 00:00:00 | ||
图片预览


文档简介
第三章 学情评估卷
一、选择题(每小题3分,共24分)
1.下列数据中不能确定物体位置的是 ( )
A.会议室5排28号 B.东经18°,北纬140°
C.小河镇文化街32号 D.北偏东30°
2.已知a<0,那么点P(-a2,5-a)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.平面直角坐标系内一点P(-3,2)关于y轴对称的点的坐标是 ( )
A.(-3,-2) B.(3,-2) C.(-2,-3) D.(3,2)
4.经过A(2,3),B(-4,3)两点作直线AB,则直线AB ( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.无法确定
5.如果点(2x,x+3)在x轴上方,且该点到x轴和y轴的距离相等,则x的值为 ( )
A.3 B.-1 C.3或-1 D.-3或1
6.在正方形网格中,点A,B,C的位置如图所示,建立适当的直角坐标系后,点B,C的坐标分别是(-3,1),(-2,-1),则点A在 ( )
(第6题)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.[2024深圳罗湖区阶段练习]如图,△AOB是边长为2的等边三角形,则点A关于x轴的对称点的坐标为 ( )
(第7题)
A.(-1,) B.(-1,-) C.(1,) D.(1,-)
8.如图,一个粒子从原点出发,每分钟运动一次,依次运动到(0,1)→(1,0)→(1,1)→ (1,2)→(2,1)→…,则第2 025分钟时粒子所在点的横坐标为 ( )
(第8题)
A.886 B.903 C.946 D.990
二、填空题(每小题3分,共15分)
9.[2024嘉兴期末]若用(3,2)表示第3排第2座,则第5排第4座可表示为 .
10.在平面直角坐标系中,点(2a+1,2a-1)在x轴上,则a的值为 .
11.已知点P(2x,3x-1)是平面直角坐标系内的点,若点P在第三象限,且到两坐标轴的距离之和为16,则x的值为 .
12.如图,长方形ABOC在直角坐标系中,点A的坐标为(-2,1),则长方形ABOC的面积为 .
(第12题)
13.[新考法 分类讨论法]如图,已知点A(2,2),点B(2,0),在坐标轴上有一点P(不与点O重合),使得点P,A,B所构成的三角形与△OAB全等,则点P的坐标为 .
(第13题)
三、解答题(共61分)
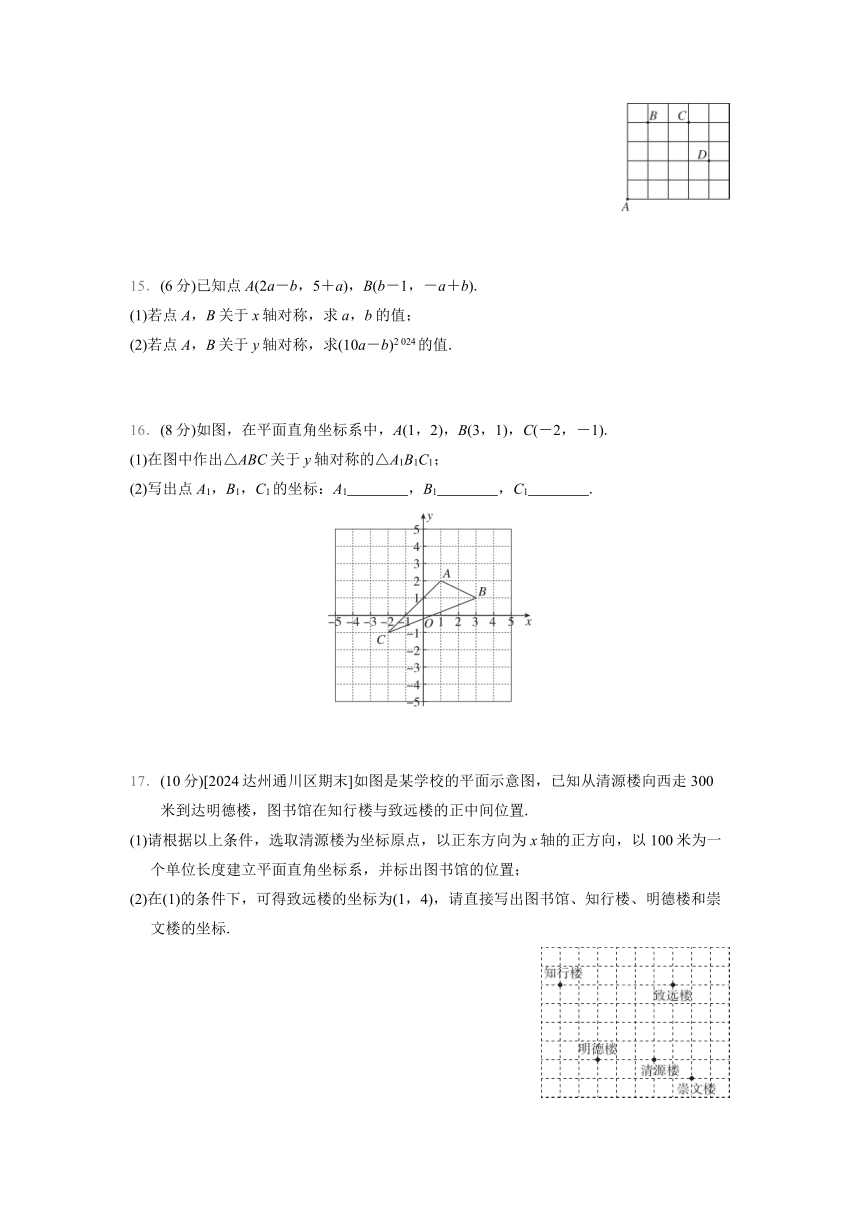
14.(6分)[2024南京江北新区阶段练习]如图,杭州亚运会数字火炬手和吉祥物琮琮、宸宸、莲莲在5×5的方格(每小格边长为1 m)上.数字火炬手沿着网格线从A处出发去寻找B,C,D处的吉祥物,规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→C( , );B→C( , );C→ (-3,-4);
(2)若数字火炬手的行走路线为A→B→C→D,则数字火炬手走过的路程为 m;
(3)若数字火炬手从A处去寻找最后一棒火炬手的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-1),请在图中标出最后一棒火炬手的位置点E.
15.(6分)已知点A(2a-b,5+a),B(b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(10a-b)2 024的值.
16.(8分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标:A1 ,B1 ,C1 .
17.(10分)[2024达州通川区期末]如图是某学校的平面示意图,已知从清源楼向西走300米到达明德楼,图书馆在知行楼与致远楼的正中间位置.
(1)请根据以上条件,选取清源楼为坐标原点,以正东方向为x轴的正方向,以100米为一个单位长度建立平面直角坐标系,并标出图书馆的位置;
(2)在(1)的条件下,可得致远楼的坐标为(1,4),请直接写出图书馆、知行楼、明德楼和崇文楼的坐标.
18.(10分)如图,在平面直角坐标系中,AC=CD,已知A(3,0),B(0,3),C(0,5),点D在第一象限内,∠DCA=90°.
(1)∠OBA的度数为 ;
(2)求点D的坐标.
19.(10分)[新视角 新定义题]在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为(-3,1),
①在点E(0,3),F(3,-3),G(2,-5)中,为点A的“等距点”的是 .
②若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为 .
(2)若T1(-1,-k-3),T2(4,4k-3)两点为“等距点”,求k的值.
20.(11分)如图,在平面直角坐标系中,点A的坐标为(0,a),点B的坐标为(b,0),点C的坐标为(2,a),a,b满足|a-2|+=0,CD⊥CB且CD=CB.
(1)点D的坐标为 ,△ACD的面积为 .
(2)小明同学在学习求坐标平面内三角形面积时学到一个新方法如下:平面直角坐标系中有△P1P2P3,其三个顶点P1(x1,y1),P2(x2,y2),P3(x3,y3)按逆时针方向排列,则△P1P2P3的面积S可用下面式子计算,S==(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2),请用此方法计算△ABD的面积.
参考答案
一、1.D 2.B 3.D 4.A 5.C 6.B 7.D
8.D
二、9.(5,4) 10. 11.-3 12.2
13.(4,0)或(0,2)
三、14.解:(1)+3;+4;+2;0;A (2)10
(3)点E如图所示.
15.解:(1)因为点A,B关于x轴对称,
所以2a-b=b-1,5+a-a+b=0,
解得a=-,b=-5.
(2)因为点A,B关于y轴对称,
所以2a-b+b-1=0,5+a=-a+b,
解得a=,b=6,
所以(10a-b)2 024=1.
16.解:(1)所作图形如图所示:
(2)(-1,2);(-3,1);(2,-1)
17.解:(1)以清源楼为坐标原点建立平面直角坐标系,标出图书馆的位置如图所示.
(2)图书馆的坐标为(-2,4),知行楼的坐标为(-5,4),明德楼的坐标为(-3,0),崇文楼的坐标为(2,-1).
18.解:(1)45°
(2)过点D作DE⊥y轴于点E,
所以∠DEC=∠COA=90°.
因为∠DCA=90°,
所以∠DCE+∠ACO=90°.
易知∠DCE+∠CDE=90°,
所以∠CDE=∠ACO.又因为CD=AC,
所以△DEC≌△COA.
所以DE=CO,EC=OA.
因为点A(3,0),点C(0,5),
所以EC=OA=3,DE=CO=5.
所以OE=EC+CO=8.
所以点D的坐标为(5,8).
19.解:(1)①E,F ②(-3,3)
(2)T1(-1,-k-3),T2(4,4k-3)两点为“等距点”,分两种情况:
①若|4k-3|≤4,则4=-k-3或-4=-k-3,
解得k=-7(舍去)或k=1.
②若|4k-3|>4,则|4k-3|=|-k-3|,
解得k=2或k=0(舍去).
根据“等距点”的定义知,k=1或k=2符合题意.
即k的值是1或2.
20.解:(1)(4,3);1
(2)由题意及(1)可知A(0,2),B(3,0),D(4,3),
所以x1=0,y1=2,x2=3,y2=0,x3=4,y3=3.
所以S=×(0×0+3×3+4×2-0×3-3×2-4×0)=.即△ABD的面积为.
一、选择题(每小题3分,共24分)
1.下列数据中不能确定物体位置的是 ( )
A.会议室5排28号 B.东经18°,北纬140°
C.小河镇文化街32号 D.北偏东30°
2.已知a<0,那么点P(-a2,5-a)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.平面直角坐标系内一点P(-3,2)关于y轴对称的点的坐标是 ( )
A.(-3,-2) B.(3,-2) C.(-2,-3) D.(3,2)
4.经过A(2,3),B(-4,3)两点作直线AB,则直线AB ( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.无法确定
5.如果点(2x,x+3)在x轴上方,且该点到x轴和y轴的距离相等,则x的值为 ( )
A.3 B.-1 C.3或-1 D.-3或1
6.在正方形网格中,点A,B,C的位置如图所示,建立适当的直角坐标系后,点B,C的坐标分别是(-3,1),(-2,-1),则点A在 ( )
(第6题)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.[2024深圳罗湖区阶段练习]如图,△AOB是边长为2的等边三角形,则点A关于x轴的对称点的坐标为 ( )
(第7题)
A.(-1,) B.(-1,-) C.(1,) D.(1,-)
8.如图,一个粒子从原点出发,每分钟运动一次,依次运动到(0,1)→(1,0)→(1,1)→ (1,2)→(2,1)→…,则第2 025分钟时粒子所在点的横坐标为 ( )
(第8题)
A.886 B.903 C.946 D.990
二、填空题(每小题3分,共15分)
9.[2024嘉兴期末]若用(3,2)表示第3排第2座,则第5排第4座可表示为 .
10.在平面直角坐标系中,点(2a+1,2a-1)在x轴上,则a的值为 .
11.已知点P(2x,3x-1)是平面直角坐标系内的点,若点P在第三象限,且到两坐标轴的距离之和为16,则x的值为 .
12.如图,长方形ABOC在直角坐标系中,点A的坐标为(-2,1),则长方形ABOC的面积为 .
(第12题)
13.[新考法 分类讨论法]如图,已知点A(2,2),点B(2,0),在坐标轴上有一点P(不与点O重合),使得点P,A,B所构成的三角形与△OAB全等,则点P的坐标为 .
(第13题)
三、解答题(共61分)
14.(6分)[2024南京江北新区阶段练习]如图,杭州亚运会数字火炬手和吉祥物琮琮、宸宸、莲莲在5×5的方格(每小格边长为1 m)上.数字火炬手沿着网格线从A处出发去寻找B,C,D处的吉祥物,规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→C( , );B→C( , );C→ (-3,-4);
(2)若数字火炬手的行走路线为A→B→C→D,则数字火炬手走过的路程为 m;
(3)若数字火炬手从A处去寻找最后一棒火炬手的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-1),请在图中标出最后一棒火炬手的位置点E.
15.(6分)已知点A(2a-b,5+a),B(b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(10a-b)2 024的值.
16.(8分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标:A1 ,B1 ,C1 .
17.(10分)[2024达州通川区期末]如图是某学校的平面示意图,已知从清源楼向西走300米到达明德楼,图书馆在知行楼与致远楼的正中间位置.
(1)请根据以上条件,选取清源楼为坐标原点,以正东方向为x轴的正方向,以100米为一个单位长度建立平面直角坐标系,并标出图书馆的位置;
(2)在(1)的条件下,可得致远楼的坐标为(1,4),请直接写出图书馆、知行楼、明德楼和崇文楼的坐标.
18.(10分)如图,在平面直角坐标系中,AC=CD,已知A(3,0),B(0,3),C(0,5),点D在第一象限内,∠DCA=90°.
(1)∠OBA的度数为 ;
(2)求点D的坐标.
19.(10分)[新视角 新定义题]在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为(-3,1),
①在点E(0,3),F(3,-3),G(2,-5)中,为点A的“等距点”的是 .
②若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为 .
(2)若T1(-1,-k-3),T2(4,4k-3)两点为“等距点”,求k的值.
20.(11分)如图,在平面直角坐标系中,点A的坐标为(0,a),点B的坐标为(b,0),点C的坐标为(2,a),a,b满足|a-2|+=0,CD⊥CB且CD=CB.
(1)点D的坐标为 ,△ACD的面积为 .
(2)小明同学在学习求坐标平面内三角形面积时学到一个新方法如下:平面直角坐标系中有△P1P2P3,其三个顶点P1(x1,y1),P2(x2,y2),P3(x3,y3)按逆时针方向排列,则△P1P2P3的面积S可用下面式子计算,S==(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2),请用此方法计算△ABD的面积.
参考答案
一、1.D 2.B 3.D 4.A 5.C 6.B 7.D
8.D
二、9.(5,4) 10. 11.-3 12.2
13.(4,0)或(0,2)
三、14.解:(1)+3;+4;+2;0;A (2)10
(3)点E如图所示.
15.解:(1)因为点A,B关于x轴对称,
所以2a-b=b-1,5+a-a+b=0,
解得a=-,b=-5.
(2)因为点A,B关于y轴对称,
所以2a-b+b-1=0,5+a=-a+b,
解得a=,b=6,
所以(10a-b)2 024=1.
16.解:(1)所作图形如图所示:
(2)(-1,2);(-3,1);(2,-1)
17.解:(1)以清源楼为坐标原点建立平面直角坐标系,标出图书馆的位置如图所示.
(2)图书馆的坐标为(-2,4),知行楼的坐标为(-5,4),明德楼的坐标为(-3,0),崇文楼的坐标为(2,-1).
18.解:(1)45°
(2)过点D作DE⊥y轴于点E,
所以∠DEC=∠COA=90°.
因为∠DCA=90°,
所以∠DCE+∠ACO=90°.
易知∠DCE+∠CDE=90°,
所以∠CDE=∠ACO.又因为CD=AC,
所以△DEC≌△COA.
所以DE=CO,EC=OA.
因为点A(3,0),点C(0,5),
所以EC=OA=3,DE=CO=5.
所以OE=EC+CO=8.
所以点D的坐标为(5,8).
19.解:(1)①E,F ②(-3,3)
(2)T1(-1,-k-3),T2(4,4k-3)两点为“等距点”,分两种情况:
①若|4k-3|≤4,则4=-k-3或-4=-k-3,
解得k=-7(舍去)或k=1.
②若|4k-3|>4,则|4k-3|=|-k-3|,
解得k=2或k=0(舍去).
根据“等距点”的定义知,k=1或k=2符合题意.
即k的值是1或2.
20.解:(1)(4,3);1
(2)由题意及(1)可知A(0,2),B(3,0),D(4,3),
所以x1=0,y1=2,x2=3,y2=0,x3=4,y3=3.
所以S=×(0×0+3×3+4×2-0×3-3×2-4×0)=.即△ABD的面积为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
