数学北师大版六年级下册《鸽巢原理》课件(共18张PPT)
文档属性
| 名称 | 数学北师大版六年级下册《鸽巢原理》课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-21 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
鸽巢原理
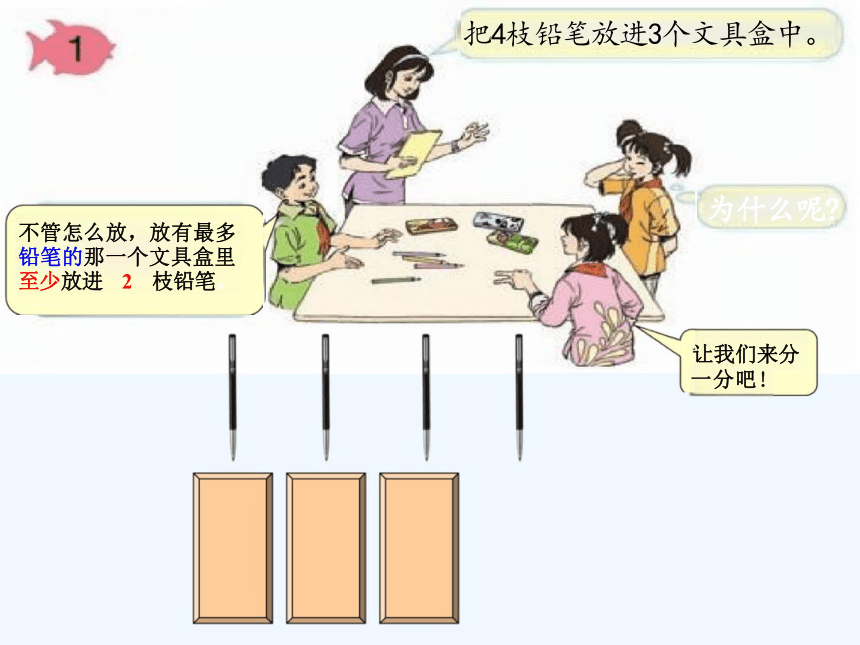
不管怎么放,放有最多 铅笔的那一个文具盒里 至少放进 2 枝铅笔。
把4枝铅笔放进3个文具盒中。
为什么呢
让我们来分 一分吧!
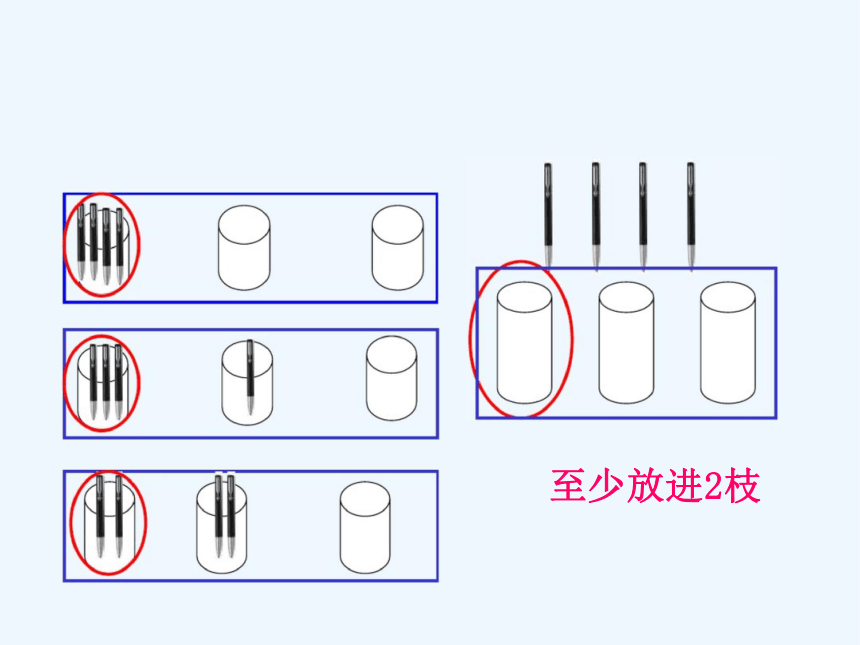
至少放进2枝
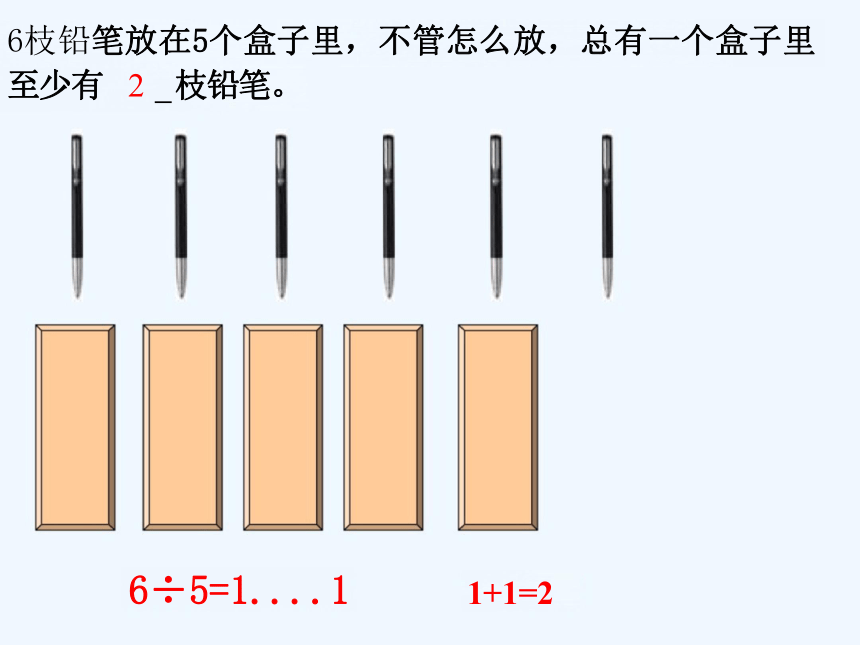
6枝铅笔放在5个盒子里,不管怎么放,总有一个盒子里
至少有 2 枝铅笔。
6÷5=1....1 1+1=2
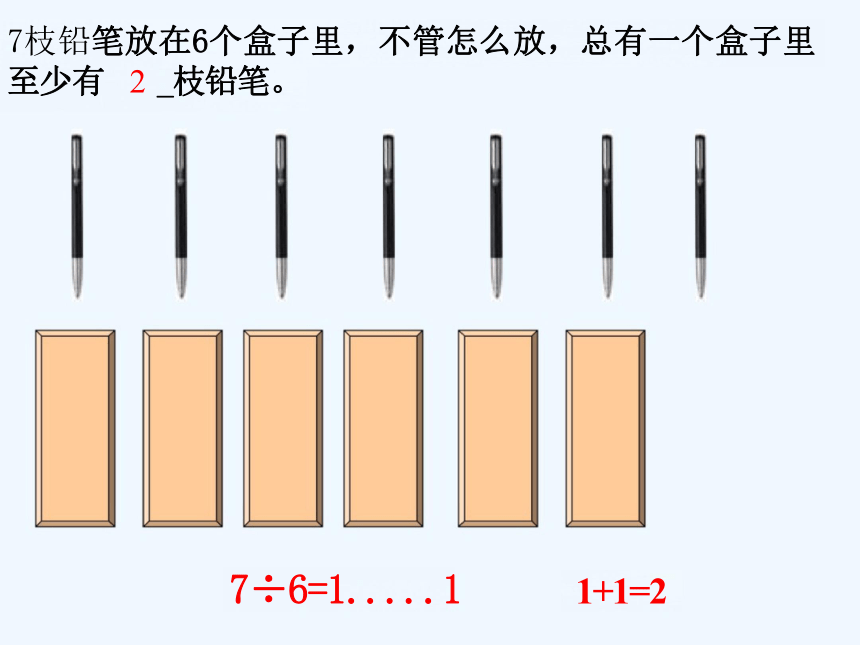
7枝铅笔放在6个盒子里,不管怎么放,总有一个盒子里
至少有 2 _枝铅笔。
7÷6=1.....1 1+1=2
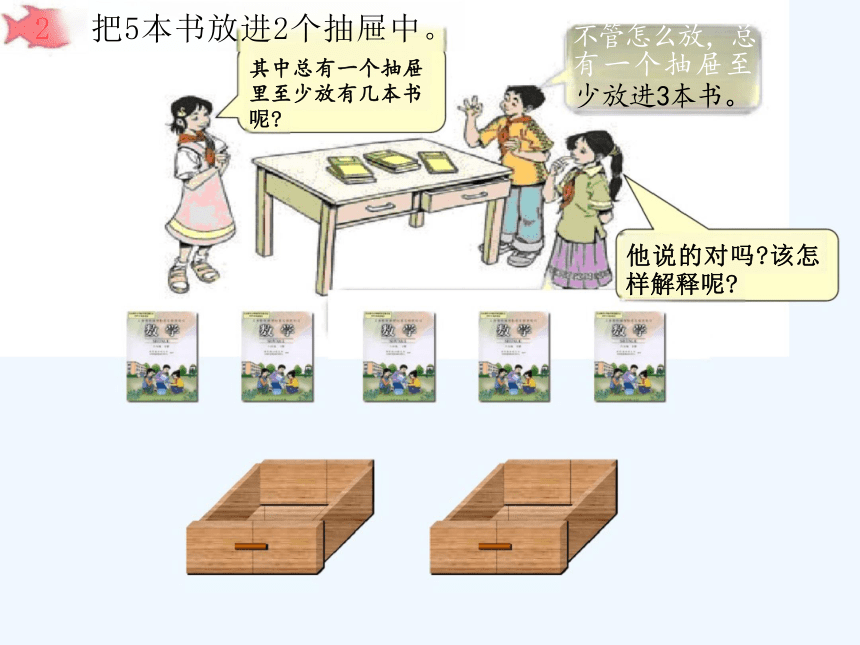
2 把5本书放进2个抽屉中。
其中总有一个抽屉 里至少放有几本书 呢
不管怎么放,总 有一个抽屉至
少放进3本书。
他说的对吗 该怎 样解释呢
7÷2=3...1
9÷2=4....1
你有什么发现
所以7本书放进2个抽
屉,有一个抽屉至少
放4本书。9本书……
如果一共有7本书会怎样呢 9本呢
我发现……
3+1=4
4+1=5
比较、思考:
1.如果把4本书放到3个抽屉里,总有一个抽屉至少
放 进 ( 2 )本书。
比较、思考:
1.如果把4本书放到3个抽屉里,总有一个抽屉至少
放 进 ( 2 ) 本 书 。
2.如果把5本书放到3个抽屉里,总有一个抽屉至少 放 进 ( 2 )本书。
特点:把一些“物体”放进到若干个“抽屉”里,求
其中装有最多物体的一个“抽屉”里至少有几个“物 体”。 (物体数多于抽屉数)
计算绝招
至少数=商数+1
做一做1
7只鸽子飞回5个鸽舍,至少有2只鸽子要飞进 同一个鸽舍里。为什么
7÷5=1......2,1+1=2,所以至少有2只鸽子
要飞进同一个鸽舍里。
做一做2
8只鸽子飞回3个鸽舍,至少有3只鸽子要飞进同 一个鸽舍。为什么
“抽屉原理”简介
“抽屉原理”最先是由19世纪的德
国数学家狄里克雷 (Dirichlet) 运用于解
决数学问题的,所以又称“狄里克雷原 理”,也称为“鸽巢原理”。“抽屉原 理”的应用却是千变万化的,用它可以 解决许多有趣的问题,并且常常能得到
些令人惊异的结果。“抽屉原理”在 数论、集合论、组合论中都得到了广泛 的应用。
“魔术”揭秘
一副扑克牌(除去大小王)52张中有四种花色,从中 随意抽5张牌,无论怎么抽,总是至少有两张牌是 同一花色的。为什么
六(2)班中至
少有5人是同
一个月出生的。
六年级里一定
有两人的生日 是同一天。
1.向东小学六年级共有370名学生,其中六(2)班有49名
370÷365=1....5
49÷12=4......1
他们说的对吗 为什么
1+1=2
4+1=5
学生。
2. 张叔叔参加飞镖比赛,投了5镖,
成绩是41环。张叔叔至少有一镖 不低于9环。为什么
41÷5=8......1,8+1=9。
所以至少有一镖不低于9环。
鸽巢原理
不管怎么放,放有最多 铅笔的那一个文具盒里 至少放进 2 枝铅笔。
把4枝铅笔放进3个文具盒中。
为什么呢
让我们来分 一分吧!
至少放进2枝
6枝铅笔放在5个盒子里,不管怎么放,总有一个盒子里
至少有 2 枝铅笔。
6÷5=1....1 1+1=2
7枝铅笔放在6个盒子里,不管怎么放,总有一个盒子里
至少有 2 _枝铅笔。
7÷6=1.....1 1+1=2
2 把5本书放进2个抽屉中。
其中总有一个抽屉 里至少放有几本书 呢
不管怎么放,总 有一个抽屉至
少放进3本书。
他说的对吗 该怎 样解释呢
7÷2=3...1
9÷2=4....1
你有什么发现
所以7本书放进2个抽
屉,有一个抽屉至少
放4本书。9本书……
如果一共有7本书会怎样呢 9本呢
我发现……
3+1=4
4+1=5
比较、思考:
1.如果把4本书放到3个抽屉里,总有一个抽屉至少
放 进 ( 2 )本书。
比较、思考:
1.如果把4本书放到3个抽屉里,总有一个抽屉至少
放 进 ( 2 ) 本 书 。
2.如果把5本书放到3个抽屉里,总有一个抽屉至少 放 进 ( 2 )本书。
特点:把一些“物体”放进到若干个“抽屉”里,求
其中装有最多物体的一个“抽屉”里至少有几个“物 体”。 (物体数多于抽屉数)
计算绝招
至少数=商数+1
做一做1
7只鸽子飞回5个鸽舍,至少有2只鸽子要飞进 同一个鸽舍里。为什么
7÷5=1......2,1+1=2,所以至少有2只鸽子
要飞进同一个鸽舍里。
做一做2
8只鸽子飞回3个鸽舍,至少有3只鸽子要飞进同 一个鸽舍。为什么
“抽屉原理”简介
“抽屉原理”最先是由19世纪的德
国数学家狄里克雷 (Dirichlet) 运用于解
决数学问题的,所以又称“狄里克雷原 理”,也称为“鸽巢原理”。“抽屉原 理”的应用却是千变万化的,用它可以 解决许多有趣的问题,并且常常能得到
些令人惊异的结果。“抽屉原理”在 数论、集合论、组合论中都得到了广泛 的应用。
“魔术”揭秘
一副扑克牌(除去大小王)52张中有四种花色,从中 随意抽5张牌,无论怎么抽,总是至少有两张牌是 同一花色的。为什么
六(2)班中至
少有5人是同
一个月出生的。
六年级里一定
有两人的生日 是同一天。
1.向东小学六年级共有370名学生,其中六(2)班有49名
370÷365=1....5
49÷12=4......1
他们说的对吗 为什么
1+1=2
4+1=5
学生。
2. 张叔叔参加飞镖比赛,投了5镖,
成绩是41环。张叔叔至少有一镖 不低于9环。为什么
41÷5=8......1,8+1=9。
所以至少有一镖不低于9环。
