2024年浙江省舟山市中考数学考前最后一卷(含答案)
文档属性
| 名称 | 2024年浙江省舟山市中考数学考前最后一卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-21 16:14:18 | ||
图片预览




文档简介
2024年舟山市中考数学考前最后一卷
1.全卷共三大题,24小题,共10页。满分120分,考试时间120分钟。
2.全卷分卷I(选择题)和卷II(非选择题)两部分,全部在答题纸上作答。卷I的答案必须用2B铅笔填涂;卷II的答案必须用黑色钢笔或签字笔写在答题纸相应位置上。
3.考试时不能使用计算器。
第I卷(选择题)
一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列各数中,倒数等于本身的是( )
A. B. C. D.2
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列二次根式,被开方数中各因式的指数都为1的是 ( )
A. B. C. D.
4.某地博物院是国家文物局公布的第一批国家一级博物馆,现有馆藏文物17 万余件(套),其中国家一级文物与国家二级文物5000多件,历史文化艺术价值极高,一部分藏品被誉为国之重器.这里的数据17万可用科学记数法表示为( )
A.人 B.人 C.人 D.人
5.如图,已知在和中,,,,若用“HL”判定,则需要添加的条件是( )
A. B.
C. D.
6.某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小舟同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于、、、四点,然后利用刻度尺量得该纸条的宽为,,.请你帮忙计算纸杯杯底的直径为( )
A. B. C. D.
7.《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设6210元购买椽的数量为x株,则符合题意的方程是( )
A. B. C. D.
8.敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10步到60步的矩形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
9.如图,以的三边为边分别向外作正方形、连结交于点,作交于点,连结交于点.若,则的值为( )
A. B. C. D.
10.根据图中数字的排列规律,在第⑩个图中,的值是( )
A. B. C.510 D.512
第II卷(非选择题)
二、填空题(本题有6小题,每题4分,共24分)
11.分解因式: .
12.如图,电路图上有三个开关,,和两个小灯泡,,随机闭合开关,,中的两个,能让其中一个小灯泡发光的概率是 .
12题图 13题图
13.如图,在正方形的边上取一点,连接,将沿翻折,点恰好与对角线上的点重合,连接,若,则的面积是 .
14.如图,物理实验课上,老师将平行于凸透镜主光轴的红光和紫光射入同一个凸透镜,折射光线,交于点,与主光轴分别交于点、,由此发现凸透镜的焦点略有偏差.若,,则的大小为 .
14题图 15题图
15.筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2,已知圆心在水面上方,且被水面截得弦长为4米,半径为2.5米.若点为运行轨道的最低点,则点到弦所在直线的距离是 米.
16.如图,在中,,连接,,以点为圆心,长为半径画弧,弧分别交、、于点、、,点是上方内一动点,点是上一动点,连接、、,则的最小值为 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)计算:;(2)先化简,再求值:,其中.
18.数学兴趣小组开展探究活动,研究了“正整数N能否表示为(均为自然数)”的问题.
(1)指导教师将学生的发现进行整理,部分信息如下(为正整数):
奇数 的倍数
表示结果
一般结论 ______
按上表规律,完成下列问题:
()( )( );
()______;
(2)兴趣小组还猜测:像这些形如(为正整数)的正整数不能表示为(均为自然数).师生一起研讨,分析过程如下:
假设,其中均为自然数. 分下列三种情形分析: 若均为偶数,设,,其中均为自然数, 则为的倍数. 而不是的倍数,矛盾.故不可能均为偶数. 若均为奇数,设,,其中均为自然数, 则______为的倍数. 而不是的倍数,矛盾.故不可能均为奇数. 若一个是奇数一个是偶数,则为奇数. 而是偶数,矛盾.故不可能一个是奇数一个是偶数. 由可知,猜测正确.
阅读以上内容,请在情形的横线上填写所缺内容.
19.已知:如图,在中,,以为直径的交于点,为的中点.
(1)求证:;
(2)延长、交于点,若,,求的长.
20.某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据以上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为______°;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
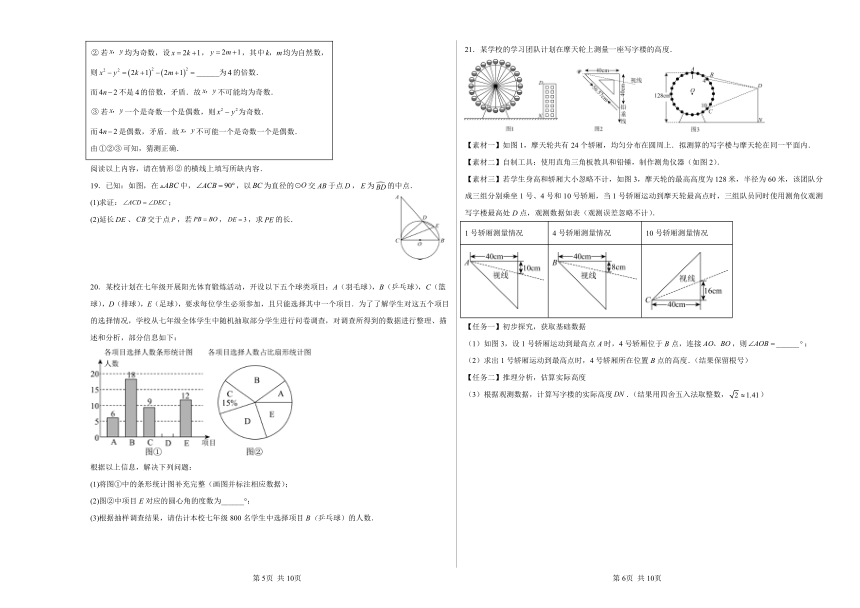
21.某学校的学习团队计划在摩天轮上测量一座写字楼的高度.
【素材一】如图1,摩天轮共有24个轿厢,均匀分布在圆周上.拟测算的写字楼与摩天轮在同一平面内.
【素材二】自制工具:使用直角三角板教具和铅锤,制作测角仪器(如图2).
【素材三】若学生身高和轿厢大小忽略不计,如图3,摩天轮的最高高度为128米,半径为60米,该团队分成三组分别乘坐1号、4号和10号轿厢,当1号轿厢运动到摩天轮最高点时,三组队员同时使用测角仪观测写字楼最高处D点,观测数据如表(观测误差忽略不计).
1号轿厢测量情况 4号轿厢测量情况 10号轿厢测量情况
【任务一】初步探究,获取基础数据
(1)如图3,设1号轿厢运动到最高点A时,4号轿厢位于B点,连接,则______;
(2)求出1号轿厢运动到最高点时,4号轿厢所在位置B点的高度.(结果保留根号)
【任务二】推理分析,估算实际高度
根据观测数据,计算写字楼的实际高度.(结果用四舍五入法取整数,)
22.某校九年级学生在数学社团课上进行了项目化学习研究,某小组研究如下:
【提出驱动性问题】如何设计无盖长方体纸盒?
【设计实践任务】选择“素材1”“素材2”设计了“任务1”“任务2”“任务3”的实践活动.请你尝试帮助他们解决相关问题.
素材1 利用一边长为的正方形纸板可能设计成如图所示的无盖纸盒.
素材2 如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖纸盒.
问题解决
任务1 设剪去的小正方形边长为,请用含的代数式表示折成的无盖长方体纸盒的侧面积.
任务2 若用上述方式折成的无盖长方体纸盒侧面积为,试求出此时纸盒的体积.
任务3 探究按上述方式折成的无盖长方体纸盒侧面积能否到达?若能,请求出此时剪去的小正方形边长;若不能,请说明理由.
23.下面是一位同学的数学学习笔记,请仔细阅读并完成任务.
用均值不等式求最值
若实数,则有,当且仅当时,取等号,我们称不等式为均值不等式.
证明:
由上可知,①当为定值的时候,有最大值;
②当为定值的时候,有最小值.
所以,利用均值不等式可以求一些函数的最值.
例:已知,求函数的最小值.
解:
,当且仅当,即时,等号成立
当即时,函数取最小值,最小值为2.
任务:
(1)若,则当_____时,代数式取最小值,最小值为______;
(2)已知若,函数,试说明当取何值时,取得最小值,并求出的最小值;
(3)如图,已知点是反比例函数图象上一动点,点,则的面积的最小值为______.
24.【课堂背景】舟山市某中学的张老师以“几何题目开放探索”为主题,开展了一节“综合与实践”的数学课.课堂上,张老师给出了这样一个图形,供同学们发挥几何思维.
【设置情景】张老师给出了如下几何图形:
“如图1,已知中,点D为边上一点,点E为外一点,连接.此时我们假设这个几何图形满足的数量关系.”
【提出问题】擅长几何的小舟同学经过思索后,为题目增加如下条件,请你帮他作答.
(1)“若,,再给出和的长度,可以求出的长度.”为了简化计算,张老师提出令,,,求的长(结果无需化简);
(2)在小舟的启发下,同学们纷纷开始积极地进行讨论.后来,小海与他的小组更改了题目的部分信息,令点E在上运动,将条件“”改为了“”,其他条件不变,想要探究边的关系.
张老师根据他们关于题目的修改,提出问题,请你解答.
【拓展探索】“如图2,已知中,点D为边上一点,点E为上一点,,若,探究、、的数量关系,并证明.
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B B A C C D B D
二、填空题(本题有6小题,共24分)
11. 12. 13./
14.145 15.1 16./
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)2;(2),
18.(1)(),;(); (2)
19.(1)证明:是的直径,
,
,
,
,
,
,
;
(2)解:连接,
为弧的中点.
,
,
,
,
∴,
,
,
,,
,
,
.
20.(1)解:总人数为,
D组人数为,
补图如下:
(2)解:,
(3)解:(人).
21.解:(1)连接、,如下图所示:
“海之跃”摩天轮共有24个轿厢,均匀分布在圆周上,其中包含了3个桥厢,
,
(2)过点作于点,
点此时的高度为最高为128米,半径为60米,
点高度为68米,
,,
,
点的高度为米,
(3)连接,,,
由素材1,素材3可得,,
则,过点作于点,
令,由素材2,素材3的4号轿厢测量情况和10号轿厢测量情况得:,,
,即,
点的高度为:(米,
22.解:任务1:
任务2:由题意得
解得
当时,
当时,
任务3:不能,当时,可得
整理得
因为
所以不能达到.
23.(1)解:∵,
∴,,
∴,
当且仅当,即,即(负值舍去)时,等号成立,
∴当时,代数式取最小值,最小值为;
(2)解:∵,
∴,
∴,
当且仅当,即(负值舍去)时,等号成立,
∴当时,函数取最小值,最小值为8;
(3)解:如图,作轴于,轴于,
∵,
∴,,
∵点是反比例函数图象上一动点,
∴设,
∴,,
∴,
∴
,
∵,
∴,,
∴,
当且仅当,即时,等号成立,
∴的面积的最小值为.
24.解:(1)如图,作,,过P作交延长线于H,
∵,
∴,
在和中,
,
∴,
∴;
在和中,
,
∴,
∴,,
∵,,
∴,,
∴,
在中,,
∴,则,
在中,,
∴,
∴;
(2)[拓展探索].
证明:如图,延长到P,使,连接,在取一点H,连接,使,
∴,,
∵,又,
∴,
∴,则,
设,则,
∵,又,
∴,又,
∴,
∴,又,
∴,
∴,,
∵,即,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
1.全卷共三大题,24小题,共10页。满分120分,考试时间120分钟。
2.全卷分卷I(选择题)和卷II(非选择题)两部分,全部在答题纸上作答。卷I的答案必须用2B铅笔填涂;卷II的答案必须用黑色钢笔或签字笔写在答题纸相应位置上。
3.考试时不能使用计算器。
第I卷(选择题)
一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列各数中,倒数等于本身的是( )
A. B. C. D.2
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列二次根式,被开方数中各因式的指数都为1的是 ( )
A. B. C. D.
4.某地博物院是国家文物局公布的第一批国家一级博物馆,现有馆藏文物17 万余件(套),其中国家一级文物与国家二级文物5000多件,历史文化艺术价值极高,一部分藏品被誉为国之重器.这里的数据17万可用科学记数法表示为( )
A.人 B.人 C.人 D.人
5.如图,已知在和中,,,,若用“HL”判定,则需要添加的条件是( )
A. B.
C. D.
6.某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小舟同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于、、、四点,然后利用刻度尺量得该纸条的宽为,,.请你帮忙计算纸杯杯底的直径为( )
A. B. C. D.
7.《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设6210元购买椽的数量为x株,则符合题意的方程是( )
A. B. C. D.
8.敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10步到60步的矩形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
9.如图,以的三边为边分别向外作正方形、连结交于点,作交于点,连结交于点.若,则的值为( )
A. B. C. D.
10.根据图中数字的排列规律,在第⑩个图中,的值是( )
A. B. C.510 D.512
第II卷(非选择题)
二、填空题(本题有6小题,每题4分,共24分)
11.分解因式: .
12.如图,电路图上有三个开关,,和两个小灯泡,,随机闭合开关,,中的两个,能让其中一个小灯泡发光的概率是 .
12题图 13题图
13.如图,在正方形的边上取一点,连接,将沿翻折,点恰好与对角线上的点重合,连接,若,则的面积是 .
14.如图,物理实验课上,老师将平行于凸透镜主光轴的红光和紫光射入同一个凸透镜,折射光线,交于点,与主光轴分别交于点、,由此发现凸透镜的焦点略有偏差.若,,则的大小为 .
14题图 15题图
15.筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2,已知圆心在水面上方,且被水面截得弦长为4米,半径为2.5米.若点为运行轨道的最低点,则点到弦所在直线的距离是 米.
16.如图,在中,,连接,,以点为圆心,长为半径画弧,弧分别交、、于点、、,点是上方内一动点,点是上一动点,连接、、,则的最小值为 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)计算:;(2)先化简,再求值:,其中.
18.数学兴趣小组开展探究活动,研究了“正整数N能否表示为(均为自然数)”的问题.
(1)指导教师将学生的发现进行整理,部分信息如下(为正整数):
奇数 的倍数
表示结果
一般结论 ______
按上表规律,完成下列问题:
()( )( );
()______;
(2)兴趣小组还猜测:像这些形如(为正整数)的正整数不能表示为(均为自然数).师生一起研讨,分析过程如下:
假设,其中均为自然数. 分下列三种情形分析: 若均为偶数,设,,其中均为自然数, 则为的倍数. 而不是的倍数,矛盾.故不可能均为偶数. 若均为奇数,设,,其中均为自然数, 则______为的倍数. 而不是的倍数,矛盾.故不可能均为奇数. 若一个是奇数一个是偶数,则为奇数. 而是偶数,矛盾.故不可能一个是奇数一个是偶数. 由可知,猜测正确.
阅读以上内容,请在情形的横线上填写所缺内容.
19.已知:如图,在中,,以为直径的交于点,为的中点.
(1)求证:;
(2)延长、交于点,若,,求的长.
20.某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据以上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为______°;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
21.某学校的学习团队计划在摩天轮上测量一座写字楼的高度.
【素材一】如图1,摩天轮共有24个轿厢,均匀分布在圆周上.拟测算的写字楼与摩天轮在同一平面内.
【素材二】自制工具:使用直角三角板教具和铅锤,制作测角仪器(如图2).
【素材三】若学生身高和轿厢大小忽略不计,如图3,摩天轮的最高高度为128米,半径为60米,该团队分成三组分别乘坐1号、4号和10号轿厢,当1号轿厢运动到摩天轮最高点时,三组队员同时使用测角仪观测写字楼最高处D点,观测数据如表(观测误差忽略不计).
1号轿厢测量情况 4号轿厢测量情况 10号轿厢测量情况
【任务一】初步探究,获取基础数据
(1)如图3,设1号轿厢运动到最高点A时,4号轿厢位于B点,连接,则______;
(2)求出1号轿厢运动到最高点时,4号轿厢所在位置B点的高度.(结果保留根号)
【任务二】推理分析,估算实际高度
根据观测数据,计算写字楼的实际高度.(结果用四舍五入法取整数,)
22.某校九年级学生在数学社团课上进行了项目化学习研究,某小组研究如下:
【提出驱动性问题】如何设计无盖长方体纸盒?
【设计实践任务】选择“素材1”“素材2”设计了“任务1”“任务2”“任务3”的实践活动.请你尝试帮助他们解决相关问题.
素材1 利用一边长为的正方形纸板可能设计成如图所示的无盖纸盒.
素材2 如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖纸盒.
问题解决
任务1 设剪去的小正方形边长为,请用含的代数式表示折成的无盖长方体纸盒的侧面积.
任务2 若用上述方式折成的无盖长方体纸盒侧面积为,试求出此时纸盒的体积.
任务3 探究按上述方式折成的无盖长方体纸盒侧面积能否到达?若能,请求出此时剪去的小正方形边长;若不能,请说明理由.
23.下面是一位同学的数学学习笔记,请仔细阅读并完成任务.
用均值不等式求最值
若实数,则有,当且仅当时,取等号,我们称不等式为均值不等式.
证明:
由上可知,①当为定值的时候,有最大值;
②当为定值的时候,有最小值.
所以,利用均值不等式可以求一些函数的最值.
例:已知,求函数的最小值.
解:
,当且仅当,即时,等号成立
当即时,函数取最小值,最小值为2.
任务:
(1)若,则当_____时,代数式取最小值,最小值为______;
(2)已知若,函数,试说明当取何值时,取得最小值,并求出的最小值;
(3)如图,已知点是反比例函数图象上一动点,点,则的面积的最小值为______.
24.【课堂背景】舟山市某中学的张老师以“几何题目开放探索”为主题,开展了一节“综合与实践”的数学课.课堂上,张老师给出了这样一个图形,供同学们发挥几何思维.
【设置情景】张老师给出了如下几何图形:
“如图1,已知中,点D为边上一点,点E为外一点,连接.此时我们假设这个几何图形满足的数量关系.”
【提出问题】擅长几何的小舟同学经过思索后,为题目增加如下条件,请你帮他作答.
(1)“若,,再给出和的长度,可以求出的长度.”为了简化计算,张老师提出令,,,求的长(结果无需化简);
(2)在小舟的启发下,同学们纷纷开始积极地进行讨论.后来,小海与他的小组更改了题目的部分信息,令点E在上运动,将条件“”改为了“”,其他条件不变,想要探究边的关系.
张老师根据他们关于题目的修改,提出问题,请你解答.
【拓展探索】“如图2,已知中,点D为边上一点,点E为上一点,,若,探究、、的数量关系,并证明.
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B B A C C D B D
二、填空题(本题有6小题,共24分)
11. 12. 13./
14.145 15.1 16./
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)2;(2),
18.(1)(),;(); (2)
19.(1)证明:是的直径,
,
,
,
,
,
,
;
(2)解:连接,
为弧的中点.
,
,
,
,
∴,
,
,
,,
,
,
.
20.(1)解:总人数为,
D组人数为,
补图如下:
(2)解:,
(3)解:(人).
21.解:(1)连接、,如下图所示:
“海之跃”摩天轮共有24个轿厢,均匀分布在圆周上,其中包含了3个桥厢,
,
(2)过点作于点,
点此时的高度为最高为128米,半径为60米,
点高度为68米,
,,
,
点的高度为米,
(3)连接,,,
由素材1,素材3可得,,
则,过点作于点,
令,由素材2,素材3的4号轿厢测量情况和10号轿厢测量情况得:,,
,即,
点的高度为:(米,
22.解:任务1:
任务2:由题意得
解得
当时,
当时,
任务3:不能,当时,可得
整理得
因为
所以不能达到.
23.(1)解:∵,
∴,,
∴,
当且仅当,即,即(负值舍去)时,等号成立,
∴当时,代数式取最小值,最小值为;
(2)解:∵,
∴,
∴,
当且仅当,即(负值舍去)时,等号成立,
∴当时,函数取最小值,最小值为8;
(3)解:如图,作轴于,轴于,
∵,
∴,,
∵点是反比例函数图象上一动点,
∴设,
∴,,
∴,
∴
,
∵,
∴,,
∴,
当且仅当,即时,等号成立,
∴的面积的最小值为.
24.解:(1)如图,作,,过P作交延长线于H,
∵,
∴,
在和中,
,
∴,
∴;
在和中,
,
∴,
∴,,
∵,,
∴,,
∴,
在中,,
∴,则,
在中,,
∴,
∴;
(2)[拓展探索].
证明:如图,延长到P,使,连接,在取一点H,连接,使,
∴,,
∵,又,
∴,
∴,则,
设,则,
∵,又,
∴,又,
∴,
∴,又,
∴,
∴,,
∵,即,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
