第十九章《一次函数》单元巩固题(无答案)人教版数学八年级下册
文档属性
| 名称 | 第十九章《一次函数》单元巩固题(无答案)人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 419.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 14:07:32 | ||
图片预览


文档简介
第十九章《一次函数》单元巩固题
班级: 姓名:
一.选择题
1、一次函数的图象与y轴交点是( )
A.(﹣1,0) B.(2,0) C.(0,1) D.(0,﹣1)
2、如图,直线yx+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为( )
A.(0,) B.(0,1) C.(1,0) D.(0,)
3、甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示,给出下列结论:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=34,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
4、如图,在平面直角坐标系中,线段AB的端点为A(﹣3,1),B(1,2),若直线y=kx﹣1与线段AB有交点,则k的值不能是( )
A.2 B.4 C.﹣2 D.﹣4
5、甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发小时后乙再出发如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是
A. 甲车的速度是,乙车的速度是
B. 的值为,的值为
C. 甲、乙两车相遇时,两车距离地
D. 甲车出发后追上乙车
6、如图,若直线与轴交于点,与轴正半轴交于,且的面积为,则该直线的解析式为
A.
B.
C.
D.
7、若一次函数的图象经过点和点,当时,,且与轴相交于正半轴,则的取值范围是
A. B. C. D.
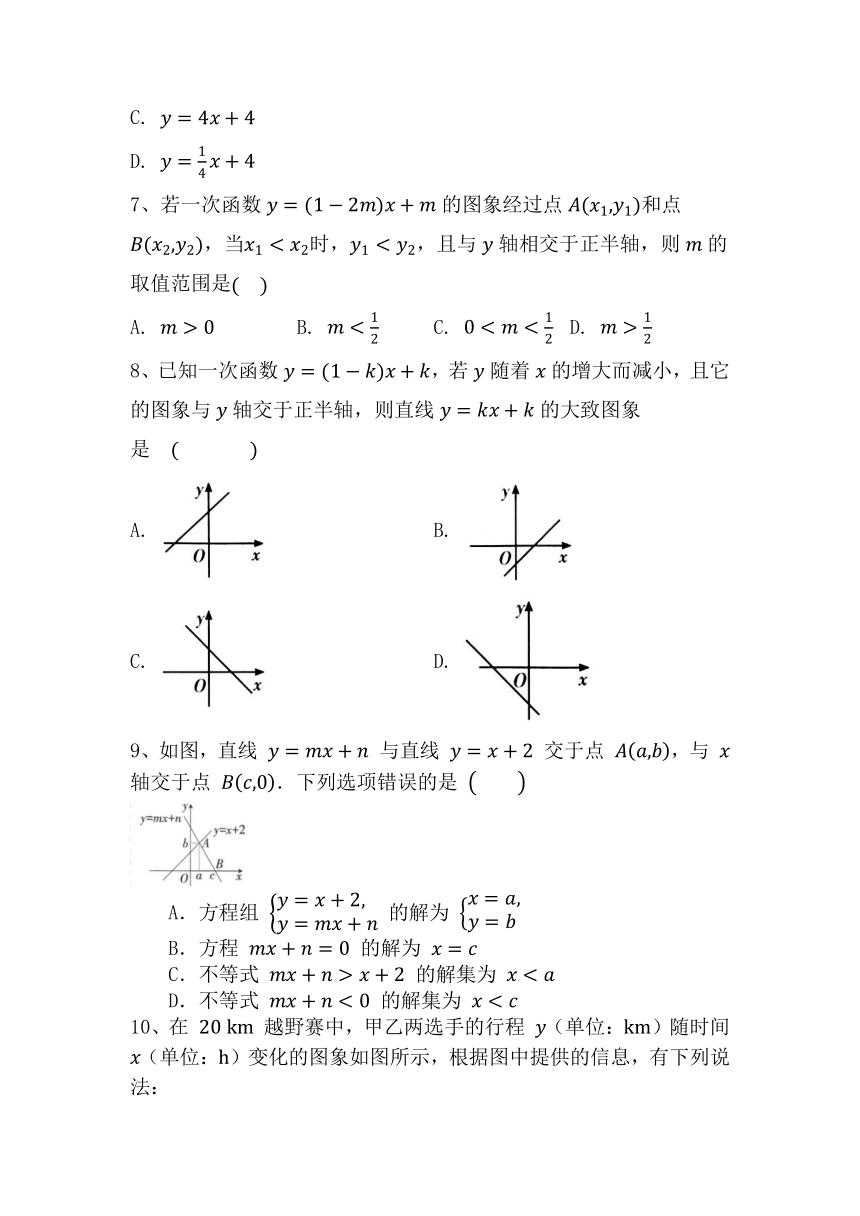
8、已知一次函数,若随着的增大而减小,且它的图象与轴交于正半轴,则直线的大致图象是
A. B.
C. D.
9、如图,直线 与直线 交于点 ,与 轴交于点 .下列选项错误的是
A.方程组 的解为
B.方程 的解为
C.不等式 的解集为
D.不等式 的解集为
10、在 越野赛中,甲乙两选手的行程 (单位:)随时间 (单位:)变化的图象如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度;
②出发后 小时,两人行程均为 ;
③出发后 小时,甲的行程比乙多 ;
④甲比乙先到达终点.
其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题
11、将直线 的图象沿 轴向上平移 个单位长度后,所得直线的函数表达式为 .
12、在函数 中,如果自变量 大于 ,那么函数值 的取值范围是 .
13、已知点 , 是直线 上的两点,且当 时,,则该直线经过 象限.
14、如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,以PC为边做等腰直角三角形PCD,∠CPD=90°,PC=PD,过点D作线段AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则Q点的坐标是 .
15、如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
三.解答题
16、如图,直线 : 与 轴交于点 ,与 轴交于点 .直线 : 经过点 ,,与直线 交于点 .
(1) 求直线 的函数关系式;
(2) 连接 ,求 的面积;
(3) 设点 的坐标为 ,求 的值使得 值最小.
17、已知一次函数,求:
为何值时,函数图象交轴于正半轴?
为何值时,函数图象与轴的交点在轴的下方?
为何值时,图象经过原点?
18、一次函数,,其中.
判断点是否在函数的图象上,并说明理由;
若函数与的图象交于点,求点的横坐标;
点,,分别在函数与的图象上,当时,若,求的取值范围.
19、已知函数是一次函数且随的增大而减小,求和的取值.
20、为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于 .下图折线表示实行阶梯水价后每月水费 (元)与用水量 ()之间的函数关系.其中线段 表示第二级阶梯时 与 之间的函数关系.
(1) 写出点 的实际意义.
(2) 求线段 所在直线的表达式.
(3) 某户 月份按照阶梯水价应缴水费 元,其相应用水量为多少 ?
21、爷爷和他的孙子小明星期天一起去爬山,来到山脚下,小明让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小明和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小明开始爬山时开始计时),请看图回答下列问题:
(1) 爷爷比小明先 米?山顶离山脚 米?
(2) 写出图中两条线段的交点表示的实际意义 .
(3) 小明在爬山过程中何时与爷爷相距 米?
22.如图,过点 的一次函数 的图象分别与 轴, 轴相交于 , 两点.
(1) 求 的值;
(2) 直线 与 轴相交于点 ,与线段 相交于点 .
(i)若直线 把 分成面积比为 的两部分,求直线 的函数表达式;
(ⅱ)连接 ,若 是以 为腰的等腰三角形,求满足条件的点 的坐标.
班级: 姓名:
一.选择题
1、一次函数的图象与y轴交点是( )
A.(﹣1,0) B.(2,0) C.(0,1) D.(0,﹣1)
2、如图,直线yx+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为( )
A.(0,) B.(0,1) C.(1,0) D.(0,)
3、甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示,给出下列结论:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=34,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
4、如图,在平面直角坐标系中,线段AB的端点为A(﹣3,1),B(1,2),若直线y=kx﹣1与线段AB有交点,则k的值不能是( )
A.2 B.4 C.﹣2 D.﹣4
5、甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发小时后乙再出发如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是
A. 甲车的速度是,乙车的速度是
B. 的值为,的值为
C. 甲、乙两车相遇时,两车距离地
D. 甲车出发后追上乙车
6、如图,若直线与轴交于点,与轴正半轴交于,且的面积为,则该直线的解析式为
A.
B.
C.
D.
7、若一次函数的图象经过点和点,当时,,且与轴相交于正半轴,则的取值范围是
A. B. C. D.
8、已知一次函数,若随着的增大而减小,且它的图象与轴交于正半轴,则直线的大致图象是
A. B.
C. D.
9、如图,直线 与直线 交于点 ,与 轴交于点 .下列选项错误的是
A.方程组 的解为
B.方程 的解为
C.不等式 的解集为
D.不等式 的解集为
10、在 越野赛中,甲乙两选手的行程 (单位:)随时间 (单位:)变化的图象如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度;
②出发后 小时,两人行程均为 ;
③出发后 小时,甲的行程比乙多 ;
④甲比乙先到达终点.
其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题
11、将直线 的图象沿 轴向上平移 个单位长度后,所得直线的函数表达式为 .
12、在函数 中,如果自变量 大于 ,那么函数值 的取值范围是 .
13、已知点 , 是直线 上的两点,且当 时,,则该直线经过 象限.
14、如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,以PC为边做等腰直角三角形PCD,∠CPD=90°,PC=PD,过点D作线段AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则Q点的坐标是 .
15、如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
三.解答题
16、如图,直线 : 与 轴交于点 ,与 轴交于点 .直线 : 经过点 ,,与直线 交于点 .
(1) 求直线 的函数关系式;
(2) 连接 ,求 的面积;
(3) 设点 的坐标为 ,求 的值使得 值最小.
17、已知一次函数,求:
为何值时,函数图象交轴于正半轴?
为何值时,函数图象与轴的交点在轴的下方?
为何值时,图象经过原点?
18、一次函数,,其中.
判断点是否在函数的图象上,并说明理由;
若函数与的图象交于点,求点的横坐标;
点,,分别在函数与的图象上,当时,若,求的取值范围.
19、已知函数是一次函数且随的增大而减小,求和的取值.
20、为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于 .下图折线表示实行阶梯水价后每月水费 (元)与用水量 ()之间的函数关系.其中线段 表示第二级阶梯时 与 之间的函数关系.
(1) 写出点 的实际意义.
(2) 求线段 所在直线的表达式.
(3) 某户 月份按照阶梯水价应缴水费 元,其相应用水量为多少 ?
21、爷爷和他的孙子小明星期天一起去爬山,来到山脚下,小明让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小明和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小明开始爬山时开始计时),请看图回答下列问题:
(1) 爷爷比小明先 米?山顶离山脚 米?
(2) 写出图中两条线段的交点表示的实际意义 .
(3) 小明在爬山过程中何时与爷爷相距 米?
22.如图,过点 的一次函数 的图象分别与 轴, 轴相交于 , 两点.
(1) 求 的值;
(2) 直线 与 轴相交于点 ,与线段 相交于点 .
(i)若直线 把 分成面积比为 的两部分,求直线 的函数表达式;
(ⅱ)连接 ,若 是以 为腰的等腰三角形,求满足条件的点 的坐标.
