2024年数学高一下学期期末总复习:单选题8大考点突破训练(含解析)-人教版A版(2019)
文档属性
| 名称 | 2024年数学高一下学期期末总复习:单选题8大考点突破训练(含解析)-人教版A版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 15:36:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024年数学高一下学期期末总复习:单选题8大考点 突破训练-人教版A版(2019)
8大考点汇总
考点1:平面向量的概念与运算
考点2:平面向量的应用
考点3:复数的四则运算
考点4:斜二测画法相关问题
考点5:简单几何体的表面积与体积
考点6:空间点、直线、面之间的位置关系
考点7:统计
考点8:概率
8大考点汇总突破训练
考点1:平面向量的概念与运算
1.若是不共线的向量,且,,,则( )
A.三点共线 B.三点共线
C.三点共线 D.三点共线
2.在等腰中,,则向量与的夹角为( )
A. B. C. D.
3.已知单位向量与的夹角为,则( )
A. B. C. D.
4.已知向量满足,且,则( )
A. B. C. D.
考点2:平面向量的应用
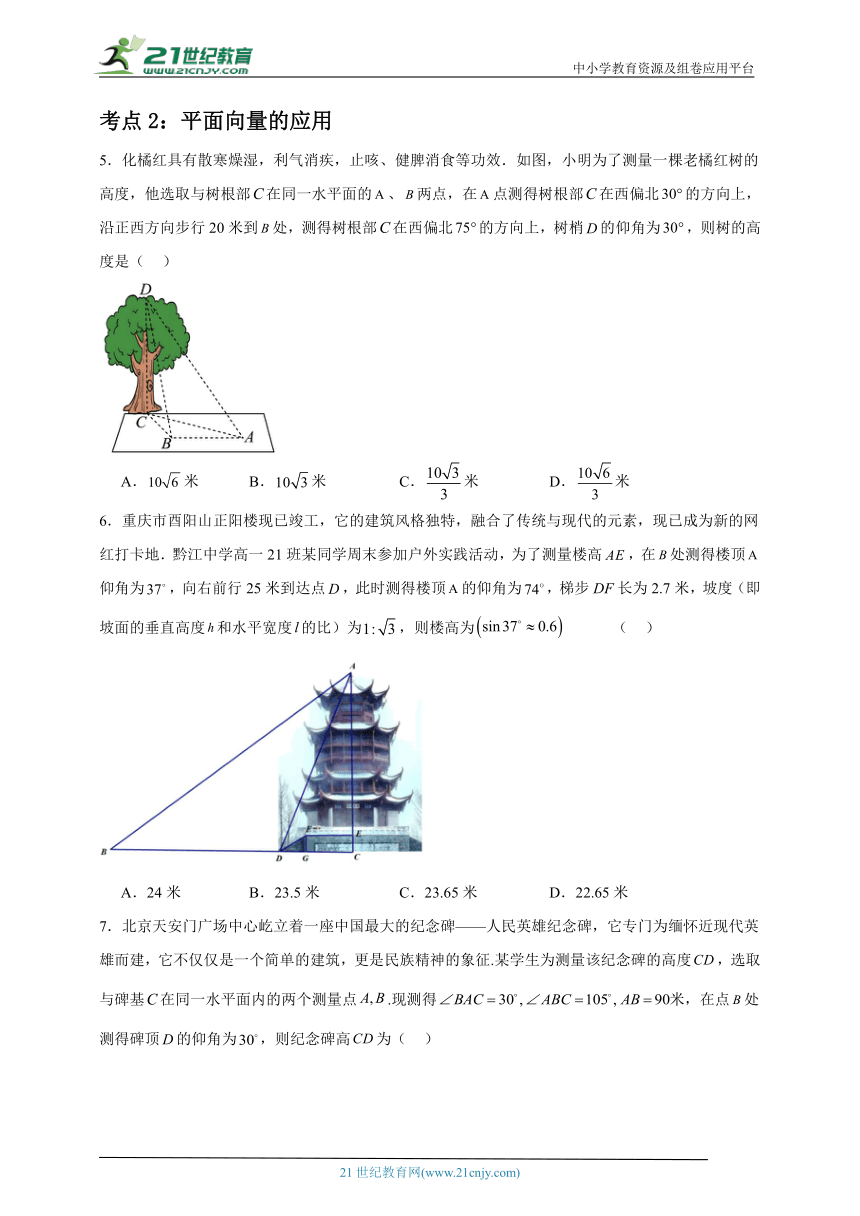
5.化橘红具有散寒燥湿,利气消疾,止咳、健脾消食等功效.如图,小明为了测量一棵老橘红树的高度,他选取与树根部在同一水平面的、两点,在点测得树根部在西偏北的方向上,沿正西方向步行20米到处,测得树根部在西偏北的方向上,树梢的仰角为,则树的高度是( )
A.米 B.米 C.米 D.米
6.重庆市酉阳山正阳楼现已竣工,它的建筑风格独特,融合了传统与现代的元素,现已成为新的网红打卡地.黔江中学高一21班某同学周末参加户外实践活动,为了测量楼高,在处测得楼顶仰角为,向右前行25米到达点,此时测得楼顶的仰角为,梯步DF长为2.7米,坡度(即坡面的垂直高度和水平宽度的比)为,则楼高为 ( )
A.24米 B.23.5米 C.23.65米 D.22.65米
7.北京天安门广场中心屹立着一座中国最大的纪念碑——人民英雄纪念碑,它专门为缅怀近现代英雄而建,它不仅仅是一个简单的建筑,更是民族精神的象征.某学生为测量该纪念碑的高度,选取与碑基在同一水平面内的两个测量点.现测得米,在点处测得碑顶的仰角为,则纪念碑高为( )
A.米 B.米 C.米 D.米
8.2023年下半年开始,某市加快了推进“5G+光网”双千兆城市建设.如图,某市区域地面有四个5G基站A,B,C,D.已知C,D两个基站建在江的南岸,距离为,基站A,B在江的北岸,测得,,,,则A,B两个基站的距离为( )
A. B. C.40km D.
考点3:复数的四则运算
9.已知复数z满足,则z的虚部为( )
A. B.1 C. D.-i
10.已知复数满足,则对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.计算:的结果是( )
A. B.
C. D.
12.若复数,,则( )
A. B. C.2 D.5
考点4:斜二测画法相关问题
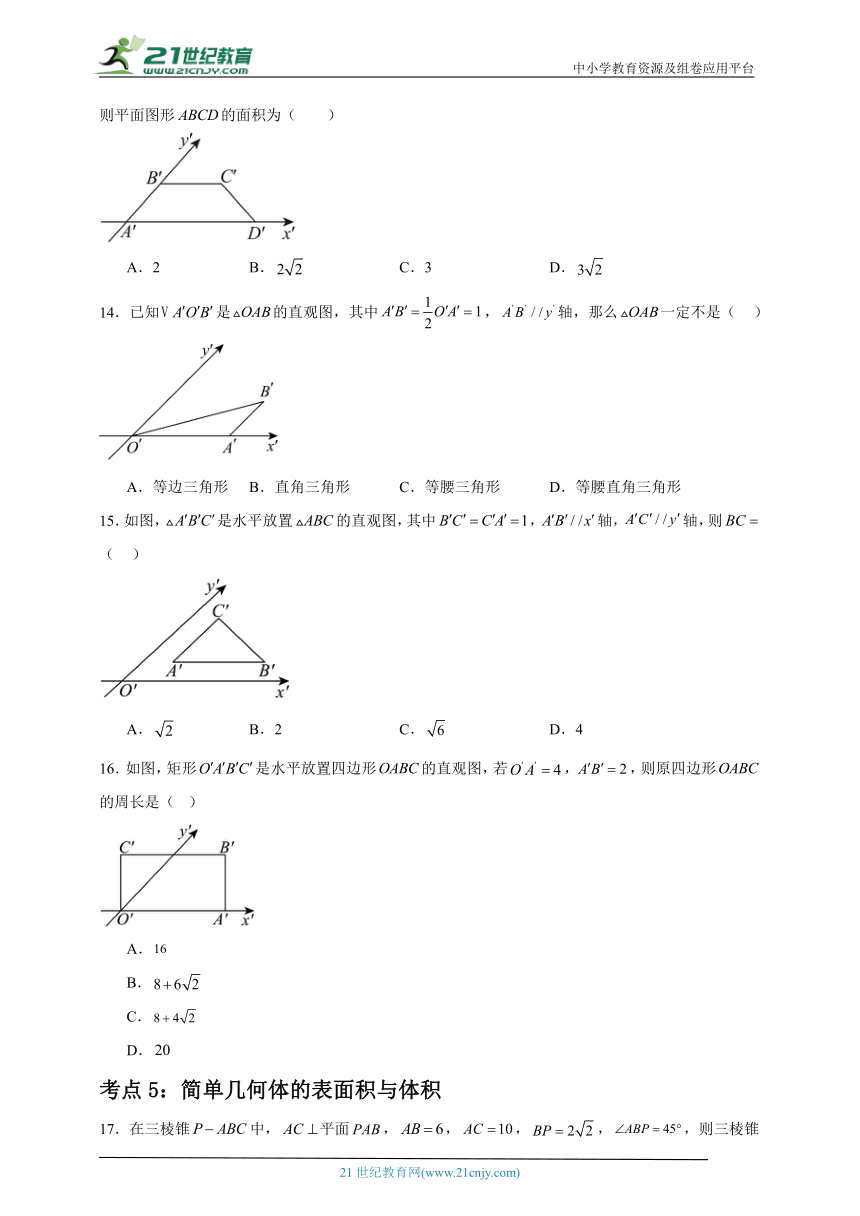
13.如图所示,梯形是平面图形ABCD用斜二测画法画出的图形,,,则平面图形的面积为( )
A.2 B. C.3 D.
14.已知是的直观图,其中,轴,那么一定不是( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
15.如图,是水平放置的直观图,其中,轴,轴,则( )
A. B.2 C. D.4
16.如图,矩形是水平放置四边形的直观图,若,,则原四边形的周长是( )
A.
B.
C.
D.
考点5:简单几何体的表面积与体积
17.在三棱锥中,平面,,,,,则三棱锥外接球的表面积为( )
A. B. C. D.
18.一个圆台的上、下底面的半径分别为1和4,体积为,则它的母线长为( )
A. B. C. D.5
19.棱长为正方体的顶点都在球面上,则该球的体积是( ).
A. B. C. D.
20.中国古代建筑中重要的构件之一——柱(俗称“柱子” 多数为木造,属于大木作范围,其中,瓜棱柱是古建筑木柱的一种做法,即木柱非整根原木,而是多块用榫卯拼合而成.宁波保国寺大殿的瓜棱柱,一部分用到了“包镶式瓜棱柱”形式,即在一根木柱周围,根据需要再用若干根一定厚度的木料包镶而成的柱子,图1为“包镶式瓜棱柱”,图2为此瓜棱柱的横截面图,中间大圆木的直径为,外部八根小圆木的直径均为,所有圆木的高度均为,且粗细均匀,则中间大圆木与一根外部小圆木的体积之比为( )
A. B.
C.3 D.
考点6:空间点、直线、面之间的位置关系
21.已知表示两条不同的直线,表示两个不重合的平面,且,下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
22.在正三棱柱中,,为棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
23.下列四个正方体中,,,为所在棱的中点,,,为正方体的三个顶点,则能得出平面平面的是( )
A. B.
C. D.
24.如图,在正方形中,E,F分别是BC,CD的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为G,且取EF中点为O,则在这个空间图形中必有( )
A. B.
C. D.
考点7:统计
25.黔江中学现有高一学生1236人,高二学生1296人,高三学生1332人,现准备采用比例分配的分层随机抽样的方法调查学生的饮食情况,从每个年级抽取一定人数的学生,其中在高二年级需抽取108人,则全校一共需要抽取的人数为( )
A.300 B.322 C.346 D.360
26.已知甲组数据由这个数据构成,记这组数据的平均数为,方差为;乙组数据由,这数据构成,记这组数据的平均数为,方差为,则( )
A., B.,
C., D.,
27.为了解中学生课外阅读情况,现从某中学随机抽取100名学生,收集了他们一周内的课外阅读时间:
一周内课外阅读时间/小时 0 1 2 3 4 5
人数 3 10 20 17 20 23 7
这100名学生的一周内课外阅读时间的分位数是( )
A. B. C. D.
28.在某学校开展的“防电信诈骗知识竞赛”活动中,高三年级部派出甲、乙、丙、丁四个小组参赛,每个小组各有10位选手.记录参赛人员失分(均为非负整数)情况,若小组的每位选手失分都不超过7分,则该组为“优秀小组”,已知选手失分数据信息如下,则一定为“优秀小组”的是( )
A.甲组中位数为3,极差为5 B.乙组平均数为2,众数为2
C.丙组平均数为2,方差为3 D.丁组平均数为2,第85百分位数为7
考点8:概率
29.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面朝上”,事件“第二枚硬币反面朝上”,则下列结论中正确的为( )
A.与互为对立事件 B.与互斥
C.与相等 D.
30.从集合中任取两个数,则这两个数的和不小于的概率是( )
A. B. C. D.
31.已知甲袋中有标号分别为1,2,3,4的四个小球,乙袋中有标号分别为2,3,4,5的四个小球,这些球除标号外完全相同,第一次从甲袋中取出一个小球,第二次从乙袋中取出一个小球,事件表示“第一次取出的小球标号为3”,事件表示“第二次取出的小球标号为偶数”,事件表示“两次取出的小球标号之和为7”,事件表示“两次取出的小球标号之和为偶数”,则( )
A.与相互独立 B.与是互斥事件
C.与是对立事件 D.与相互独立
32.学生甲想参加某高中校蓝球投篮特长生考试,测试规则如下:①投篮分为两轮,每轮均有两次机会,第一轮在罚球线处,第二轮在三分线处;②若他在罚球线处投进第一球,则直接进入下一轮,若第一次没有投进可以进行第二次投篮,投进则进入下一轮,否则不预录取;③若他在三分线处投进第一球,则直接录取,若第一次没有投进可以进行第二次投篮,投进则录取,否则不预录取.已知学生甲在罚球线处投篮命中率为,在三分线处投篮命中率为,假设学生甲每次投进与否互不影响.则学生甲共投篮三次就结束考试得概率为( )
A. B. C. D.
参考答案:
1.A
【分析】根据题意,结合共线向量的定义和判定方法,逐项判定,即可求解.
【详解】对于A中,由向量,,,
可得,所以,所以三点共线,所以A正确;
对于B中,由向量,,
设,可得,所以,此时方程组无解,
所以三点不共线,所以B错误;
对于C中,由向量,,,
可得,设,即,
所以,此时方程组无解,所以三点不共线,所以C错误;
对于D中,向量,,
设,即,所以,此时方程组无解,
所以三点不共线,所以D错误.
故选:A.
2.D
【分析】由题意可知,结合平面向量的概念即可求解.
【详解】因为为等腰直角三角形,,所以,
故向量与的夹角为.
故选:D
3.C
【分析】根据给定条件,利用数量积的定义、数量的运算律,结合垂直关系的向量表示求解即得.
【详解】依题意,,由,得,
所以.
故选:C
4.D
【分析】根据已知条件分别求出,,,在求出,,即可求解.
【详解】因为,所以,所以,
即,所以,即,
,,,即;
,,,即;
,
,
,
所以.
故选:D
5.D
【分析】根据图形,在中利用正弦定理求得的值,在中求出的值.
【详解】依题意可得如下图形,
在中,,,,
由正弦定理得,,解得,,
在中,,
所以,.
所以树的高度为米.
故选:D.
6.D
【分析】在中,米,由余弦定理可得米,在中可求的米,由坡度(即坡面的垂直高度和水平宽度的比)为得米,即可求解.
【详解】由,,得,
故米,由得,
在中由余弦定理可得,
解得米,
故米,
由坡度(即坡面的垂直高度和水平宽度的比)为得,
故米,
故楼高米.
故选:.
7.A
【分析】中,利用正弦定理求出,在中,,代入求值即可.
【详解】在中,,
由正弦定理得,即,解得,
在中,.
故选:A
8.D
【分析】利用的边角关系求出,在中利用正弦定理求出,在中利用余弦定理求出即可.
【详解】在中,,,
所以,即,得故.
在中,.
由正弦定理得,,
解得,
在中,由余弦定理得,
,
解得,即两个基站、之间的距离为.
故选:D.
9.A
【分析】由求出复数,从而可求出其虚部.
【详解】由,得,
所以z的虚部为,
故选:A
10.D
【分析】设根据复数的乘法运算法则,求出复数,即可求解.
【详解】设,由,
得,
,解得,
故对于的点位于第四象限,
故选:D.
11.D
【分析】根据复数代数形式的运算法则计算可得.
【详解】.
故选:D
12.B
【分析】根据复数的减法运算和复数的几何意义即可求解.
【详解】因为,,
所以.
故选:B
13.C
【分析】利用斜二测画法画出平面图形为直角梯形,再求面积.
【详解】如图,
作平面直角坐标系,使A与O重合,AD在x轴上,
且,AB在y轴上,且,
过B作,且,则四边形ABCD为原平面图形,为直角梯形,
其面积为.
故选:C.
14.A
【分析】利用斜二测画法还原,从而分析得是等腰直角三角形,由此得解.
【详解】依题意,还原,如图,
因为,轴,
所以,轴,则,
所以是等腰直角三角形,即A符合题意,BCD不符合题意.
故选:A.
15.C
【分析】借助余弦定理计算可得直观图中的长度,结合斜二测画法可知形状及边长,即可得.
【详解】在,,,
由余弦定理可得:,
即,而,解得,
由斜二测画法可知:中,,,,
故.
故选:C.
16.D
【分析】根据斜二测画法还原图形,由长度关系可求得结果.
【详解】设交轴于点,
根据斜二测画法可还原出原四边形如下图所示,
因为,所以,
又,且四边形为平行四边形,
,四边形的周长为.
故选:D.
17.C
【分析】在中利用余弦定理求出,利用正弦定理求出外接圆的半径,设三棱锥外接球的半径为,则,再由球的表面积公式计算可得.
【详解】在中由余弦定理
,所以,
设外接圆的半径为,则,所以,
又平面,,设三棱锥外接球的半径为,
则,
所以三棱锥外接球的表面积.
故选:C
18.D
【分析】根据圆台的体积求出圆台的高,利用圆台轴截面基本量的计算求解母线长即可.
【详解】设圆台的高为h,则圆台的体积为,解得,
所以圆台的母线长为.
故选:D.
19.B
【分析】由正方体外接球的直径即为正方体的体对角线来求出球的半径,然后利用球的体积公式即可算出答案.
【详解】∵棱长为的正方体的顶点都在同一个球面上,
∴球的直径为,半径为,
∴球的体积.
故选:B.
20.D
【分析】八根小圆木截面圆的圆心构成一个正八边形,边长为,相邻两根小圆木圆心与大圆木圆心构成一个底边长为,腰长为,顶角为的等腰三角形,结合余弦定理可得,从而可求结论.
【详解】八根小圆木截面圆的圆心构成一个正八边形,边长为,
相邻两根小圆木圆心与大圆木圆心构成一个底边长为,腰长为,顶角为的等腰三角形,
根据余弦定理,得,
解得,
所以中间大圆木与一根外部小圆木的体积之比为:
.
故选:D.
21.C
【分析】根据题意,结合线面位置关系的判定定理和性质定理,逐项判定,即可求解.
【详解】对于A中,由,则平面与平面平行或相交,所以A不正确;
对于B中,由,则直线或,所以B不正确;
对于C中,如图所示,过直线作平面,使得,
因为,且,可得,又因为,所以,
因为,可得,所以C正确;
对于D中, 由,则直线与平面平行、相交或,所以D不正确.
故选:C.
22.D
【分析】记的中点为,连接,在等腰三角形中即可得解.
【详解】记的中点为,连接,
因为为棱的中点,所以,
易知,
所以为等腰三角形,为锐角,
所以即为异面直线与所成角,
记的中点为,则,
即异面直线与所成角的余弦值为.
故选:D
23.B
【分析】利用反证法可判断A选项;利用面面平行的判定定理可判断B选项;利用反证法结合面面平行的性质可判断C选项;利用面面平行的判定和性质定理、结合反证法可判断D选项.
【详解】对于A选项,若平面平面,平面,则平面,
由图可知与平面相交,故平面与平面不平行,A不满足条件;
对于B选项,如下图所示,连接,
因为、分别为、的中点,则,
在正方体中,且,
故四边形为平行四边形,所以,,,
平面,平面,平面,
同理可证平面,,因此,平面平面,B满足条件;
对于C选项,如下图所示:
在正方体中,若平面平面,且平面平面,
则平面平面,但这与平面与平面相交矛盾,
因此,平面与平面不平行,C不满足条件;
对于D选项,在正方体中,连接、、,如下图所示:
因为且,则四边形为平行四边形,则,
平面,平面,所以,平面,
同理可证平面,,所以,平面平面,
若平面平面,则平面平面,
这与平面与平面相交矛盾,故平面与平面不平行,D不满足条件.
故选:B.
24.C
【分析】根据给定条件,证明平面,再逐项分析判断即得.
【详解】依题意,平面,则平面,
而平面,因此,而不重合,C正确,A错误;
显然,B错误;
若,而,平面,
则平面,又平面,于是,
在中,为斜边的中点,,矛盾,D错误.
故选:C
25.B
【分析】借助分层抽样的性质计算即可得.
【详解】全校一共需要抽取的人数为 人.
故选:B.
26.D
【分析】利用平均数公式可得出的大小关系,由方差公式可得出的大小关系.
【详解】由已知可得,
,
,
,
所以ABC错误,D正确.
故选:D.
27.A
【分析】根据百分位计算规则计算可得.
【详解】因为,又,
所以这名学生的一周内阅读时间的分位数为从小到大排列的第与第两数的平均数,
即为.
故选:A
28.C
【分析】A选项,假设有选手失8分,根据极差得到最低失分为3分,中位数为3,故A错误;C选项,根据方差得到,若有选手失8分,则有,矛盾,故C正确;BD选项,举出反例即可判断.
【详解】A选项,假设存在选手失分超过7分,失8分,根据极差为5,得到最低失分为3分,
此时中位数为3,故假设可以成立,故A错误;
B选项,假设乙组的失分情况为,
满足平均数为2,众数为2,但该组不为“优秀小组”,B错误;
C选项,丙组的失分情况从小到大排列依次为,
丙组平均数为2,方差为3,即,
若,则,不合要求,故,
所以该组每位选手失分都不超过7分,则该组为“优秀小组”,故C正确;
D选项,,故从小到大,选取第9个数作为第85百分位数,
即从小到大第9个数为7,假设丁组失分情况为,
满足平均数为2,第85百分位数为7,但不是“优秀小组”,故D错误.
故选:C.
29.D
【分析】分析、表示的所有情况,结合对立事件、互斥事件与相等事件的定义即可得A、B、C;借助古典概型概率公式计算可得D.
【详解】因为抛掷两枚质地均匀的硬币包含第一枚硬币正面朝上第二枚硬币正面朝上,
第一枚硬币正面朝上第二枚硬币反面朝上,第一枚硬币反面朝上第二枚硬币正面朝上,
第一枚硬币反面朝上第二枚硬币反面朝上,4种情况,
其中事件包含第一枚硬币正面朝上第二枚硬币正面朝上,
第一枚硬币正面朝上第二枚硬币反面朝上2种情况,
事件包含第一枚硬币正面朝上第二枚硬币反面朝上,
第一枚硬币反面朝上第二枚硬币反面朝上2种情况,
所以与不互斥,也不对立,也不相等,,
所以A、B、C错误,D正确,
故选:D.
30.C
【分析】列出所有可能结果,再由古典概型的概率公式计算可得.
【详解】从集合中任取两个数所有可能结果有、、、
、、、、、、共个,
其中满足两个数的和不小于的有、、、、、、、共个,
所以这两个数的和不小于的概率.
故选:C
31.D
【分析】根据互斥事件、对立事件及相互独立事件的定义判断即可.
【详解】由题意可得基本事件总数为,
设,
,
,
,
由题意可得与可以同时发生,故不是互斥事件,故B错误;
易知与不同时发生,即与为互斥事件,
但不是对立事件,比如当发生时与均不发生,故C错误.
又,
则,,
从而与不相互独立,与相互独立,故A错误,D正确.
故选:D
32.B
【分析】根据独立事件概率的乘法公式及互斥事件和的概率公式求解.
【详解】记事件表示“甲在罚球线处投篮,第次投进”,事件表示“甲在三分线处投篮,第次投进,事件表示“甲共投篮三次就结束考试”.
则,
故选:B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024年数学高一下学期期末总复习:单选题8大考点 突破训练-人教版A版(2019)
8大考点汇总
考点1:平面向量的概念与运算
考点2:平面向量的应用
考点3:复数的四则运算
考点4:斜二测画法相关问题
考点5:简单几何体的表面积与体积
考点6:空间点、直线、面之间的位置关系
考点7:统计
考点8:概率
8大考点汇总突破训练
考点1:平面向量的概念与运算
1.若是不共线的向量,且,,,则( )
A.三点共线 B.三点共线
C.三点共线 D.三点共线
2.在等腰中,,则向量与的夹角为( )
A. B. C. D.
3.已知单位向量与的夹角为,则( )
A. B. C. D.
4.已知向量满足,且,则( )
A. B. C. D.
考点2:平面向量的应用
5.化橘红具有散寒燥湿,利气消疾,止咳、健脾消食等功效.如图,小明为了测量一棵老橘红树的高度,他选取与树根部在同一水平面的、两点,在点测得树根部在西偏北的方向上,沿正西方向步行20米到处,测得树根部在西偏北的方向上,树梢的仰角为,则树的高度是( )
A.米 B.米 C.米 D.米
6.重庆市酉阳山正阳楼现已竣工,它的建筑风格独特,融合了传统与现代的元素,现已成为新的网红打卡地.黔江中学高一21班某同学周末参加户外实践活动,为了测量楼高,在处测得楼顶仰角为,向右前行25米到达点,此时测得楼顶的仰角为,梯步DF长为2.7米,坡度(即坡面的垂直高度和水平宽度的比)为,则楼高为 ( )
A.24米 B.23.5米 C.23.65米 D.22.65米
7.北京天安门广场中心屹立着一座中国最大的纪念碑——人民英雄纪念碑,它专门为缅怀近现代英雄而建,它不仅仅是一个简单的建筑,更是民族精神的象征.某学生为测量该纪念碑的高度,选取与碑基在同一水平面内的两个测量点.现测得米,在点处测得碑顶的仰角为,则纪念碑高为( )
A.米 B.米 C.米 D.米
8.2023年下半年开始,某市加快了推进“5G+光网”双千兆城市建设.如图,某市区域地面有四个5G基站A,B,C,D.已知C,D两个基站建在江的南岸,距离为,基站A,B在江的北岸,测得,,,,则A,B两个基站的距离为( )
A. B. C.40km D.
考点3:复数的四则运算
9.已知复数z满足,则z的虚部为( )
A. B.1 C. D.-i
10.已知复数满足,则对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.计算:的结果是( )
A. B.
C. D.
12.若复数,,则( )
A. B. C.2 D.5
考点4:斜二测画法相关问题
13.如图所示,梯形是平面图形ABCD用斜二测画法画出的图形,,,则平面图形的面积为( )
A.2 B. C.3 D.
14.已知是的直观图,其中,轴,那么一定不是( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
15.如图,是水平放置的直观图,其中,轴,轴,则( )
A. B.2 C. D.4
16.如图,矩形是水平放置四边形的直观图,若,,则原四边形的周长是( )
A.
B.
C.
D.
考点5:简单几何体的表面积与体积
17.在三棱锥中,平面,,,,,则三棱锥外接球的表面积为( )
A. B. C. D.
18.一个圆台的上、下底面的半径分别为1和4,体积为,则它的母线长为( )
A. B. C. D.5
19.棱长为正方体的顶点都在球面上,则该球的体积是( ).
A. B. C. D.
20.中国古代建筑中重要的构件之一——柱(俗称“柱子” 多数为木造,属于大木作范围,其中,瓜棱柱是古建筑木柱的一种做法,即木柱非整根原木,而是多块用榫卯拼合而成.宁波保国寺大殿的瓜棱柱,一部分用到了“包镶式瓜棱柱”形式,即在一根木柱周围,根据需要再用若干根一定厚度的木料包镶而成的柱子,图1为“包镶式瓜棱柱”,图2为此瓜棱柱的横截面图,中间大圆木的直径为,外部八根小圆木的直径均为,所有圆木的高度均为,且粗细均匀,则中间大圆木与一根外部小圆木的体积之比为( )
A. B.
C.3 D.
考点6:空间点、直线、面之间的位置关系
21.已知表示两条不同的直线,表示两个不重合的平面,且,下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
22.在正三棱柱中,,为棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
23.下列四个正方体中,,,为所在棱的中点,,,为正方体的三个顶点,则能得出平面平面的是( )
A. B.
C. D.
24.如图,在正方形中,E,F分别是BC,CD的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为G,且取EF中点为O,则在这个空间图形中必有( )
A. B.
C. D.
考点7:统计
25.黔江中学现有高一学生1236人,高二学生1296人,高三学生1332人,现准备采用比例分配的分层随机抽样的方法调查学生的饮食情况,从每个年级抽取一定人数的学生,其中在高二年级需抽取108人,则全校一共需要抽取的人数为( )
A.300 B.322 C.346 D.360
26.已知甲组数据由这个数据构成,记这组数据的平均数为,方差为;乙组数据由,这数据构成,记这组数据的平均数为,方差为,则( )
A., B.,
C., D.,
27.为了解中学生课外阅读情况,现从某中学随机抽取100名学生,收集了他们一周内的课外阅读时间:
一周内课外阅读时间/小时 0 1 2 3 4 5
人数 3 10 20 17 20 23 7
这100名学生的一周内课外阅读时间的分位数是( )
A. B. C. D.
28.在某学校开展的“防电信诈骗知识竞赛”活动中,高三年级部派出甲、乙、丙、丁四个小组参赛,每个小组各有10位选手.记录参赛人员失分(均为非负整数)情况,若小组的每位选手失分都不超过7分,则该组为“优秀小组”,已知选手失分数据信息如下,则一定为“优秀小组”的是( )
A.甲组中位数为3,极差为5 B.乙组平均数为2,众数为2
C.丙组平均数为2,方差为3 D.丁组平均数为2,第85百分位数为7
考点8:概率
29.抛掷两枚质地均匀的硬币,设事件“第一枚硬币正面朝上”,事件“第二枚硬币反面朝上”,则下列结论中正确的为( )
A.与互为对立事件 B.与互斥
C.与相等 D.
30.从集合中任取两个数,则这两个数的和不小于的概率是( )
A. B. C. D.
31.已知甲袋中有标号分别为1,2,3,4的四个小球,乙袋中有标号分别为2,3,4,5的四个小球,这些球除标号外完全相同,第一次从甲袋中取出一个小球,第二次从乙袋中取出一个小球,事件表示“第一次取出的小球标号为3”,事件表示“第二次取出的小球标号为偶数”,事件表示“两次取出的小球标号之和为7”,事件表示“两次取出的小球标号之和为偶数”,则( )
A.与相互独立 B.与是互斥事件
C.与是对立事件 D.与相互独立
32.学生甲想参加某高中校蓝球投篮特长生考试,测试规则如下:①投篮分为两轮,每轮均有两次机会,第一轮在罚球线处,第二轮在三分线处;②若他在罚球线处投进第一球,则直接进入下一轮,若第一次没有投进可以进行第二次投篮,投进则进入下一轮,否则不预录取;③若他在三分线处投进第一球,则直接录取,若第一次没有投进可以进行第二次投篮,投进则录取,否则不预录取.已知学生甲在罚球线处投篮命中率为,在三分线处投篮命中率为,假设学生甲每次投进与否互不影响.则学生甲共投篮三次就结束考试得概率为( )
A. B. C. D.
参考答案:
1.A
【分析】根据题意,结合共线向量的定义和判定方法,逐项判定,即可求解.
【详解】对于A中,由向量,,,
可得,所以,所以三点共线,所以A正确;
对于B中,由向量,,
设,可得,所以,此时方程组无解,
所以三点不共线,所以B错误;
对于C中,由向量,,,
可得,设,即,
所以,此时方程组无解,所以三点不共线,所以C错误;
对于D中,向量,,
设,即,所以,此时方程组无解,
所以三点不共线,所以D错误.
故选:A.
2.D
【分析】由题意可知,结合平面向量的概念即可求解.
【详解】因为为等腰直角三角形,,所以,
故向量与的夹角为.
故选:D
3.C
【分析】根据给定条件,利用数量积的定义、数量的运算律,结合垂直关系的向量表示求解即得.
【详解】依题意,,由,得,
所以.
故选:C
4.D
【分析】根据已知条件分别求出,,,在求出,,即可求解.
【详解】因为,所以,所以,
即,所以,即,
,,,即;
,,,即;
,
,
,
所以.
故选:D
5.D
【分析】根据图形,在中利用正弦定理求得的值,在中求出的值.
【详解】依题意可得如下图形,
在中,,,,
由正弦定理得,,解得,,
在中,,
所以,.
所以树的高度为米.
故选:D.
6.D
【分析】在中,米,由余弦定理可得米,在中可求的米,由坡度(即坡面的垂直高度和水平宽度的比)为得米,即可求解.
【详解】由,,得,
故米,由得,
在中由余弦定理可得,
解得米,
故米,
由坡度(即坡面的垂直高度和水平宽度的比)为得,
故米,
故楼高米.
故选:.
7.A
【分析】中,利用正弦定理求出,在中,,代入求值即可.
【详解】在中,,
由正弦定理得,即,解得,
在中,.
故选:A
8.D
【分析】利用的边角关系求出,在中利用正弦定理求出,在中利用余弦定理求出即可.
【详解】在中,,,
所以,即,得故.
在中,.
由正弦定理得,,
解得,
在中,由余弦定理得,
,
解得,即两个基站、之间的距离为.
故选:D.
9.A
【分析】由求出复数,从而可求出其虚部.
【详解】由,得,
所以z的虚部为,
故选:A
10.D
【分析】设根据复数的乘法运算法则,求出复数,即可求解.
【详解】设,由,
得,
,解得,
故对于的点位于第四象限,
故选:D.
11.D
【分析】根据复数代数形式的运算法则计算可得.
【详解】.
故选:D
12.B
【分析】根据复数的减法运算和复数的几何意义即可求解.
【详解】因为,,
所以.
故选:B
13.C
【分析】利用斜二测画法画出平面图形为直角梯形,再求面积.
【详解】如图,
作平面直角坐标系,使A与O重合,AD在x轴上,
且,AB在y轴上,且,
过B作,且,则四边形ABCD为原平面图形,为直角梯形,
其面积为.
故选:C.
14.A
【分析】利用斜二测画法还原,从而分析得是等腰直角三角形,由此得解.
【详解】依题意,还原,如图,
因为,轴,
所以,轴,则,
所以是等腰直角三角形,即A符合题意,BCD不符合题意.
故选:A.
15.C
【分析】借助余弦定理计算可得直观图中的长度,结合斜二测画法可知形状及边长,即可得.
【详解】在,,,
由余弦定理可得:,
即,而,解得,
由斜二测画法可知:中,,,,
故.
故选:C.
16.D
【分析】根据斜二测画法还原图形,由长度关系可求得结果.
【详解】设交轴于点,
根据斜二测画法可还原出原四边形如下图所示,
因为,所以,
又,且四边形为平行四边形,
,四边形的周长为.
故选:D.
17.C
【分析】在中利用余弦定理求出,利用正弦定理求出外接圆的半径,设三棱锥外接球的半径为,则,再由球的表面积公式计算可得.
【详解】在中由余弦定理
,所以,
设外接圆的半径为,则,所以,
又平面,,设三棱锥外接球的半径为,
则,
所以三棱锥外接球的表面积.
故选:C
18.D
【分析】根据圆台的体积求出圆台的高,利用圆台轴截面基本量的计算求解母线长即可.
【详解】设圆台的高为h,则圆台的体积为,解得,
所以圆台的母线长为.
故选:D.
19.B
【分析】由正方体外接球的直径即为正方体的体对角线来求出球的半径,然后利用球的体积公式即可算出答案.
【详解】∵棱长为的正方体的顶点都在同一个球面上,
∴球的直径为,半径为,
∴球的体积.
故选:B.
20.D
【分析】八根小圆木截面圆的圆心构成一个正八边形,边长为,相邻两根小圆木圆心与大圆木圆心构成一个底边长为,腰长为,顶角为的等腰三角形,结合余弦定理可得,从而可求结论.
【详解】八根小圆木截面圆的圆心构成一个正八边形,边长为,
相邻两根小圆木圆心与大圆木圆心构成一个底边长为,腰长为,顶角为的等腰三角形,
根据余弦定理,得,
解得,
所以中间大圆木与一根外部小圆木的体积之比为:
.
故选:D.
21.C
【分析】根据题意,结合线面位置关系的判定定理和性质定理,逐项判定,即可求解.
【详解】对于A中,由,则平面与平面平行或相交,所以A不正确;
对于B中,由,则直线或,所以B不正确;
对于C中,如图所示,过直线作平面,使得,
因为,且,可得,又因为,所以,
因为,可得,所以C正确;
对于D中, 由,则直线与平面平行、相交或,所以D不正确.
故选:C.
22.D
【分析】记的中点为,连接,在等腰三角形中即可得解.
【详解】记的中点为,连接,
因为为棱的中点,所以,
易知,
所以为等腰三角形,为锐角,
所以即为异面直线与所成角,
记的中点为,则,
即异面直线与所成角的余弦值为.
故选:D
23.B
【分析】利用反证法可判断A选项;利用面面平行的判定定理可判断B选项;利用反证法结合面面平行的性质可判断C选项;利用面面平行的判定和性质定理、结合反证法可判断D选项.
【详解】对于A选项,若平面平面,平面,则平面,
由图可知与平面相交,故平面与平面不平行,A不满足条件;
对于B选项,如下图所示,连接,
因为、分别为、的中点,则,
在正方体中,且,
故四边形为平行四边形,所以,,,
平面,平面,平面,
同理可证平面,,因此,平面平面,B满足条件;
对于C选项,如下图所示:
在正方体中,若平面平面,且平面平面,
则平面平面,但这与平面与平面相交矛盾,
因此,平面与平面不平行,C不满足条件;
对于D选项,在正方体中,连接、、,如下图所示:
因为且,则四边形为平行四边形,则,
平面,平面,所以,平面,
同理可证平面,,所以,平面平面,
若平面平面,则平面平面,
这与平面与平面相交矛盾,故平面与平面不平行,D不满足条件.
故选:B.
24.C
【分析】根据给定条件,证明平面,再逐项分析判断即得.
【详解】依题意,平面,则平面,
而平面,因此,而不重合,C正确,A错误;
显然,B错误;
若,而,平面,
则平面,又平面,于是,
在中,为斜边的中点,,矛盾,D错误.
故选:C
25.B
【分析】借助分层抽样的性质计算即可得.
【详解】全校一共需要抽取的人数为 人.
故选:B.
26.D
【分析】利用平均数公式可得出的大小关系,由方差公式可得出的大小关系.
【详解】由已知可得,
,
,
,
所以ABC错误,D正确.
故选:D.
27.A
【分析】根据百分位计算规则计算可得.
【详解】因为,又,
所以这名学生的一周内阅读时间的分位数为从小到大排列的第与第两数的平均数,
即为.
故选:A
28.C
【分析】A选项,假设有选手失8分,根据极差得到最低失分为3分,中位数为3,故A错误;C选项,根据方差得到,若有选手失8分,则有,矛盾,故C正确;BD选项,举出反例即可判断.
【详解】A选项,假设存在选手失分超过7分,失8分,根据极差为5,得到最低失分为3分,
此时中位数为3,故假设可以成立,故A错误;
B选项,假设乙组的失分情况为,
满足平均数为2,众数为2,但该组不为“优秀小组”,B错误;
C选项,丙组的失分情况从小到大排列依次为,
丙组平均数为2,方差为3,即,
若,则,不合要求,故,
所以该组每位选手失分都不超过7分,则该组为“优秀小组”,故C正确;
D选项,,故从小到大,选取第9个数作为第85百分位数,
即从小到大第9个数为7,假设丁组失分情况为,
满足平均数为2,第85百分位数为7,但不是“优秀小组”,故D错误.
故选:C.
29.D
【分析】分析、表示的所有情况,结合对立事件、互斥事件与相等事件的定义即可得A、B、C;借助古典概型概率公式计算可得D.
【详解】因为抛掷两枚质地均匀的硬币包含第一枚硬币正面朝上第二枚硬币正面朝上,
第一枚硬币正面朝上第二枚硬币反面朝上,第一枚硬币反面朝上第二枚硬币正面朝上,
第一枚硬币反面朝上第二枚硬币反面朝上,4种情况,
其中事件包含第一枚硬币正面朝上第二枚硬币正面朝上,
第一枚硬币正面朝上第二枚硬币反面朝上2种情况,
事件包含第一枚硬币正面朝上第二枚硬币反面朝上,
第一枚硬币反面朝上第二枚硬币反面朝上2种情况,
所以与不互斥,也不对立,也不相等,,
所以A、B、C错误,D正确,
故选:D.
30.C
【分析】列出所有可能结果,再由古典概型的概率公式计算可得.
【详解】从集合中任取两个数所有可能结果有、、、
、、、、、、共个,
其中满足两个数的和不小于的有、、、、、、、共个,
所以这两个数的和不小于的概率.
故选:C
31.D
【分析】根据互斥事件、对立事件及相互独立事件的定义判断即可.
【详解】由题意可得基本事件总数为,
设,
,
,
,
由题意可得与可以同时发生,故不是互斥事件,故B错误;
易知与不同时发生,即与为互斥事件,
但不是对立事件,比如当发生时与均不发生,故C错误.
又,
则,,
从而与不相互独立,与相互独立,故A错误,D正确.
故选:D
32.B
【分析】根据独立事件概率的乘法公式及互斥事件和的概率公式求解.
【详解】记事件表示“甲在罚球线处投篮,第次投进”,事件表示“甲在三分线处投篮,第次投进,事件表示“甲共投篮三次就结束考试”.
则,
故选:B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
