六年级下册数学人教版6 比例尺课件(共19张PPT)
文档属性
| 名称 | 六年级下册数学人教版6 比例尺课件(共19张PPT) |
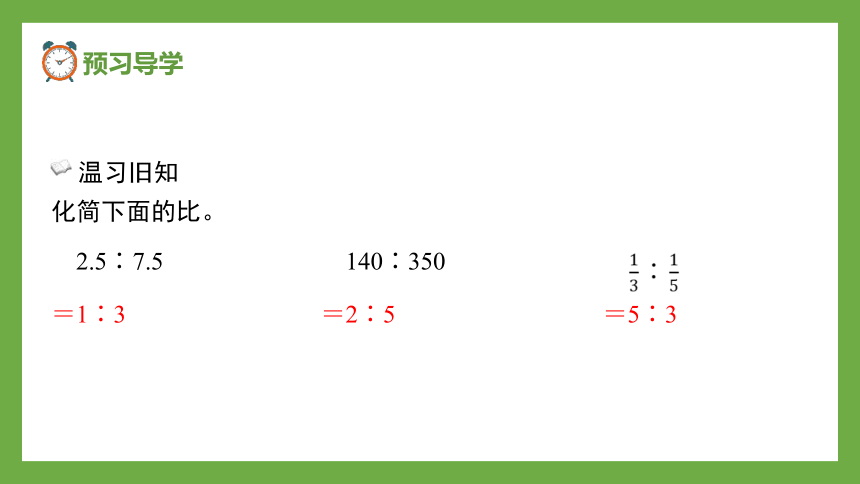
|
|
| 格式 | pptx | ||
| 文件大小 | 684.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 11:16:04 | ||
图片预览
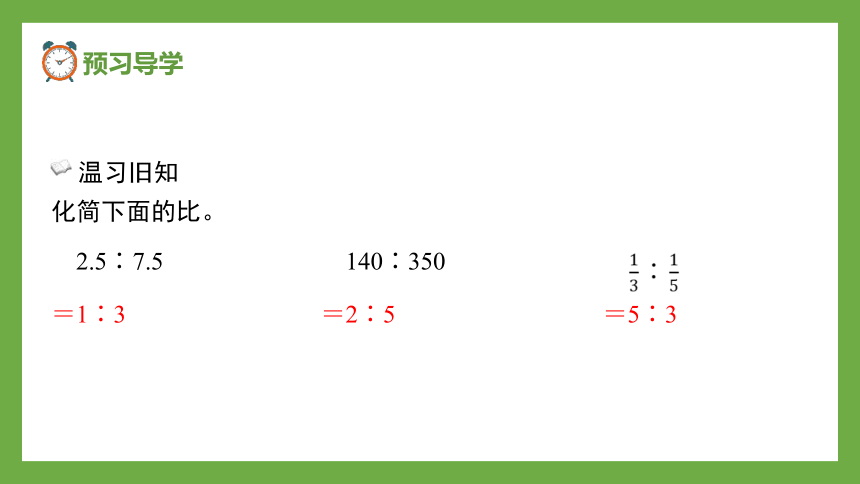






文档简介
(共19张PPT)
温习旧知
化简下面的比。
=2.5∶7.5
=140∶350
= ∶
=1∶3
=2∶5
=5∶3
男女出生的比例:18世纪法国的数学家拉普拉斯,曾用统计的
知识统计了伦敦、彼得堡、柏林几座城市以及法国全国婴儿的出生
情况。经过持续10年的研究发现,男婴在所有婴儿中的比例约为
,约等于 0.512。
预习新知
一、课前自学“比例尺”例1,完成温习旧知,复习化简比的知识。
二、课堂中和同学合作交流图上距离、实际距离、比例尺的概念,探
究比例尺的求法。
三、课堂中和老师一起总结比例尺的概念,比例尺的写法,求比例尺
的方法。
第四单元 比例
6 比例尺(1)
1. 认识比例尺,理解比例尺的意义,会求一幅图的比例尺。
2. 明确比例尺的不同类型,学会数值比例尺与线段比例尺的互相
改写。
3. 体会数学与生活的密切联系,感受数学知识的魅力。
任务驱动一:阅读教材“比例尺”的相关内容,回答下列问题。
1. 什么是比例尺?
2. 已知一幅图中两个地点之间的图上距离和实际距离,如何求这幅图
的比例尺?
3. 例如一幅图的比例尺是1∶2500,它表示图上距离是实际距离的
( ),也表示( )是( )的2500倍。
任务驱动二:探究比例尺的类型、改写和意义。
1. 比例尺有哪些类型?它们表示的意义是什么?
2. 小组讨论,写出不同类型之间比例尺的互化方法和步骤。
(1)线段比例尺改写成数值比例尺的方法:
(2)数值比例尺改写成线段比例尺的方法:
3. 比较1∶100000和2∶1有什么区别,再小组讨论放大比例尺的
意义。
任务驱动三:仔细阅读例1的内容,已知图上距离和实际距离,求
出比例尺。计算时该注意些什么?
1. 一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
2. 已知图上距离和实际距离,求比例尺的方法:先把图上距离和
实际距离统一单位,再用图上距离比实际距离就可以求出比例尺。
一、填空。
1. 甲、乙两地相距48 km,画在一幅地图上的长度为6 cm,这幅地图
的比例尺是( 1∶800000 )。
2. 是一个( 线段 )比例尺,它表示图上( 1 )cm的距离
相当于实际距离( 80 )km,把它改写成数值比例尺是
( 1∶8000000 )。
3.1∶4000000是一个( 数值 )比例尺,它表示图上( 1 )cm
的距离相当于实际距离( 40 )km,把它改写成线段比例尺是
( )。
1∶800000
线段
1
80
1∶8000000
数值
1
40
二、一种精密零件长2 mm,画在图纸上长4 cm,求这张图纸的比
例尺。
4 cm∶2 mm=40 mm∶2 mm=20∶1
答:这张图纸的比例尺是20∶1。
三、人民路的实际长度是3500米,在图上长5厘米,求出这幅图的比
例尺,并将这幅图的比例尺用线段比例尺表示出来。
3500米=350000厘米
5∶350000=1∶70000
用线段比例尺表示是 。
答:这幅图的比例尺是1∶70000,用线段比例尺表示是 。
四、找一幅地图,在地图上找出比例尺,并向家长解释地图上比例尺
的含义。( 实践类作业)
略
基础作业
一、填空题。
1. ( 图上距离 )和( 实际距离 )的比,叫作这幅图的比
例尺。
2. 把比例尺1∶1000000改写成线段比例尺是( )。
3. 小乐外出参观游览,在所拍的照片上天安门城楼高69.4毫米,天安
门城楼实际高34.7米,这张照片的比例尺是( 1∶500 )。
图上距离
实际距离
1∶500
二、将合适的比例尺的序号填在括号里。
1. 图上距离是实际距离的六百万分之一。( B )
2. 图上1厘米表示实际6000米。( A )
3. 实际距离是图上距离的6000倍。( C )
4. ( D )
A. 1∶600000 B. 1∶6000000
C. 1∶6000 D. 1∶60000000
B
A
C
D
拓展作业
三、甲、乙两地之间的实际距离是700千米,在一幅地图上量得甲、
乙两地之间的距离是10厘米,求这幅地图的比例尺。
10厘米∶700千米
=10厘米∶70000000厘米
=1∶7000000
答:这幅地图的比例尺是1∶7000000。
四、在一幢教学楼的平面图上,量得教学楼长16厘米、宽7.2厘米。
已知教学楼的实际长度是40米,实际宽度是18米,这幅平面图的比例
尺是多少?
图上距离∶实际距离
=16厘米∶40米
=16厘米∶4000厘米
=1∶250
答:这幅平面图的比例尺是1∶250。
感谢观看
下节课再会
温习旧知
化简下面的比。
=2.5∶7.5
=140∶350
= ∶
=1∶3
=2∶5
=5∶3
男女出生的比例:18世纪法国的数学家拉普拉斯,曾用统计的
知识统计了伦敦、彼得堡、柏林几座城市以及法国全国婴儿的出生
情况。经过持续10年的研究发现,男婴在所有婴儿中的比例约为
,约等于 0.512。
预习新知
一、课前自学“比例尺”例1,完成温习旧知,复习化简比的知识。
二、课堂中和同学合作交流图上距离、实际距离、比例尺的概念,探
究比例尺的求法。
三、课堂中和老师一起总结比例尺的概念,比例尺的写法,求比例尺
的方法。
第四单元 比例
6 比例尺(1)
1. 认识比例尺,理解比例尺的意义,会求一幅图的比例尺。
2. 明确比例尺的不同类型,学会数值比例尺与线段比例尺的互相
改写。
3. 体会数学与生活的密切联系,感受数学知识的魅力。
任务驱动一:阅读教材“比例尺”的相关内容,回答下列问题。
1. 什么是比例尺?
2. 已知一幅图中两个地点之间的图上距离和实际距离,如何求这幅图
的比例尺?
3. 例如一幅图的比例尺是1∶2500,它表示图上距离是实际距离的
( ),也表示( )是( )的2500倍。
任务驱动二:探究比例尺的类型、改写和意义。
1. 比例尺有哪些类型?它们表示的意义是什么?
2. 小组讨论,写出不同类型之间比例尺的互化方法和步骤。
(1)线段比例尺改写成数值比例尺的方法:
(2)数值比例尺改写成线段比例尺的方法:
3. 比较1∶100000和2∶1有什么区别,再小组讨论放大比例尺的
意义。
任务驱动三:仔细阅读例1的内容,已知图上距离和实际距离,求
出比例尺。计算时该注意些什么?
1. 一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
2. 已知图上距离和实际距离,求比例尺的方法:先把图上距离和
实际距离统一单位,再用图上距离比实际距离就可以求出比例尺。
一、填空。
1. 甲、乙两地相距48 km,画在一幅地图上的长度为6 cm,这幅地图
的比例尺是( 1∶800000 )。
2. 是一个( 线段 )比例尺,它表示图上( 1 )cm的距离
相当于实际距离( 80 )km,把它改写成数值比例尺是
( 1∶8000000 )。
3.1∶4000000是一个( 数值 )比例尺,它表示图上( 1 )cm
的距离相当于实际距离( 40 )km,把它改写成线段比例尺是
( )。
1∶800000
线段
1
80
1∶8000000
数值
1
40
二、一种精密零件长2 mm,画在图纸上长4 cm,求这张图纸的比
例尺。
4 cm∶2 mm=40 mm∶2 mm=20∶1
答:这张图纸的比例尺是20∶1。
三、人民路的实际长度是3500米,在图上长5厘米,求出这幅图的比
例尺,并将这幅图的比例尺用线段比例尺表示出来。
3500米=350000厘米
5∶350000=1∶70000
用线段比例尺表示是 。
答:这幅图的比例尺是1∶70000,用线段比例尺表示是 。
四、找一幅地图,在地图上找出比例尺,并向家长解释地图上比例尺
的含义。( 实践类作业)
略
基础作业
一、填空题。
1. ( 图上距离 )和( 实际距离 )的比,叫作这幅图的比
例尺。
2. 把比例尺1∶1000000改写成线段比例尺是( )。
3. 小乐外出参观游览,在所拍的照片上天安门城楼高69.4毫米,天安
门城楼实际高34.7米,这张照片的比例尺是( 1∶500 )。
图上距离
实际距离
1∶500
二、将合适的比例尺的序号填在括号里。
1. 图上距离是实际距离的六百万分之一。( B )
2. 图上1厘米表示实际6000米。( A )
3. 实际距离是图上距离的6000倍。( C )
4. ( D )
A. 1∶600000 B. 1∶6000000
C. 1∶6000 D. 1∶60000000
B
A
C
D
拓展作业
三、甲、乙两地之间的实际距离是700千米,在一幅地图上量得甲、
乙两地之间的距离是10厘米,求这幅地图的比例尺。
10厘米∶700千米
=10厘米∶70000000厘米
=1∶7000000
答:这幅地图的比例尺是1∶7000000。
四、在一幢教学楼的平面图上,量得教学楼长16厘米、宽7.2厘米。
已知教学楼的实际长度是40米,实际宽度是18米,这幅平面图的比例
尺是多少?
图上距离∶实际距离
=16厘米∶40米
=16厘米∶4000厘米
=1∶250
答:这幅平面图的比例尺是1∶250。
感谢观看
下节课再会
