七年级数学下册沪科版 第8章《整式的乘法与因式分解》章节检测卷(含解析)
文档属性
| 名称 | 七年级数学下册沪科版 第8章《整式的乘法与因式分解》章节检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 14:36:38 | ||
图片预览




文档简介
第8章《整式的乘法与因式分解》章节检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知,,则的值为( )
A.9 B.7 C.5 D.3
2.已知,,,,则a、b、c、d的大小关系是( )
A. B. C. D.
3.若的结果中不含项,则a、b满足的数量关系为( )
A. B. C. D.
4.将多项式除以后得商式,余式为0,则的值为( )
A.3 B.23 C.25 D.29
5.已知在中,、为整数,能使这个因式分解过程成立的的值共有( )个
A.4 B.5 C.8 D.10
6.已知,,,则的值为
A.0 B.1 C.2 D.3
7.的个位数字为( )
A.5 B.1 C.2 D.4
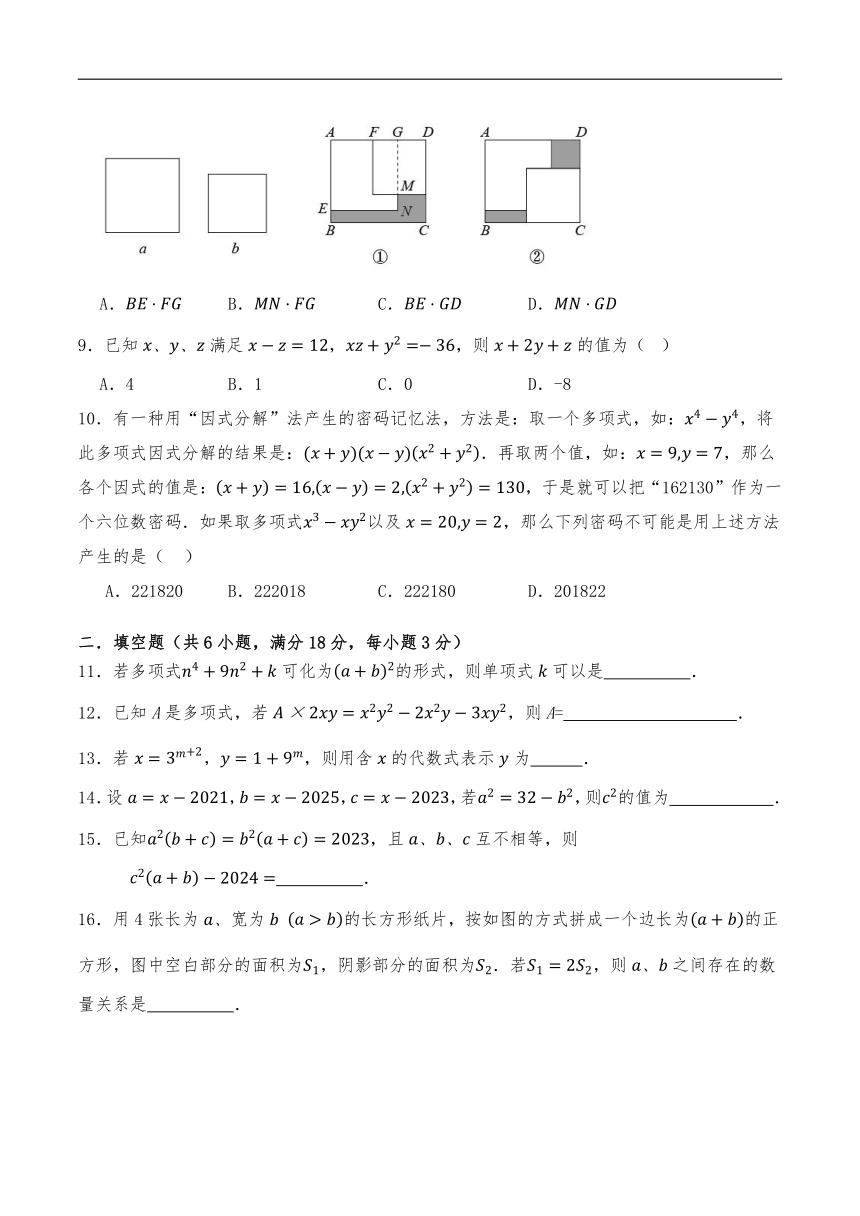
8.在矩形内,将两张边长分别为和的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,若图①中阴影部分面积为,图②中阴影部分的面积和为.则的值表示正确的是( )
A. B. C. D.
9.已知满足,,则的值为( )
A.4 B.1 C.0 D.-8
10.有一种用“因式分解”法产生的密码记忆法,方法是:取一个多项式,如:,将此多项式因式分解的结果是:.再取两个值,如:,那么各个因式的值是:,于是就可以把“162130”作为一个六位数密码.如果取多项式以及,那么下列密码不可能是用上述方法产生的是( )
A.221820 B.222018 C.222180 D.201822
二.填空题(共6小题,满分18分,每小题3分)
11.若多项式可化为的形式,则单项式可以是 .
12.已知A是多项式,若,则A= .
13.若,,则用含的代数式表示为 .
14.设,,,若,则的值为 .
15.已知,且互不相等,则 .
16.用4张长为宽为 的长方形纸片,按如图的方式拼成一个边长为的正方形,图中空白部分的面积为,阴影部分的面积为.若,则之间存在的数量关系是 .
三.解答题(共7小题,满分52分)
17.(6分)已知
(1)求的值; (2)求的值.
18.(6分)分解因式:
(1); (2).
19.(8分)已知,,且与的3倍的差的值与的取值无关,求代数式的值.
20.(8分)阅读材料,完成相应任务:“贾宪三角”又称“杨辉三角”,在欧洲则称为“帕斯卡三角”(如图所示),它揭示了(n为非负数)展开式的各项系数的规律.
根据上述规律,完成下列问题:
(1)直接写出_________.
(2)的展开式中a项的系数是__________.
(3)利用上述规律求的值,写出过程.
21.(8分)阅读理解:
若满足,求的值.
解:设,,
则,,
.
解决问题
(1)若满足,则 ;
(2)若满足,求的值;
(3)如图,在长方形中,,,点,是,上的点,且,分别以,为边在长方形外侧作正方形和,若长方形的面积为50平方单位,则图中阴影部分的面积和为 平方单位.
22.(8分)阅读并思考:
计算时,山桂娜同学发现了一个简单的口算方法,具体步骤如下:
第一步:47接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
(1)依此方法计算49:
第一步:49接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
(2)请你根据山桂娜同学的方法,填写出一个正确的计算公式.
.
(3)利用乘法运算说明第(2)小题中这个公式的正确性.
(4)写出利用这个公式计算的过程.
(5)计算也有一个简单的口算方法,具体步骤如下:
第一步:;
第二步:;
第三步:前面两步的结果综合起来,的结果是4221.
写出上述过程所依据的计算公式_______________________.
(6)利用乘法运算说明第(5)小题中这个公式的正确性.
23.(8分)阅读:证明命题“一个三位数各位数字之和可以被3整除,则这个数就可以被3整除”.
设表示一个三位数,
则
因为能被3整除,如果也能被3整除,那么就能被3整除.
(1)①一个四位数,如果能被9整除,证明能被9整除;
②若一个五位数能被9整除,则______;
(2)若一个三位数的各位数字是任意三个连续的正整数,则的最小正因数一定是______(数字“1”除外);
(3)由数字1至9组成的一个九位数,这个数的第一位能被1整除,前两位组成的两位数能被2整除,前三位组成的三位数能被3整除,以此类推,一直到整个九位数能被9整除,写出这个九位数是______.
答案解析
选择题
1.B
【分析】根据幂的乘方的逆运算和同底数幂的乘法的逆运算,求得,即可求解.
【详解】解:由可得
∴
∴
故选:B
2.A
【分析】先变形化简,,,,比较11次幂的底数大小即可.
【详解】因为,,,,
因为,
所以,
所以,
故即;
同理可证
所以,
故选A.
3.C
【分析】原式利用多项式乘多项式法则计算,合并后根据结果不含项,即可求出a与b的值.
【详解】解:
∵不含项,
∴,
∴,
故选:C.
4.D
【分析】先把整式化简,然后由整式的乘法、除法运算进行运算,求出a、b、c的值,即可得到答案.
【详解】解:
=;
∵,
∴,,,
∴,,,
∴;
故选:D.
5.B
【分析】先根据整式的乘法可得,再根据“为整数”进行分析即可得.
【详解】,
,
,
根据为整数,有以下10种情况:
(1)当时,;
(2)当时,;
(3)当时,;
(4)当时,;
(5)当时,;
(6)当时,;
(7)当时,;
(8)当时,;
(9)当时,;
(10)当时,;
综上,符合条件的m的值为,共有5个,
故选:B.
6.D
【分析】根据,,,可以得到,,的值,然后将所求式子变形,再将,,的值代入计算即可.
【详解】解:,,,
,,,
,
故选:D.
7.B
【分析】将变形为,利用平方差公式求解.
【详解】解:
,
∵ ,,,,……
可知个位数变化规律为:3,9,7,1,4次一个循环,
∴的个位数为1,
∴的个位数为0,
∴的个位数可能是0或5,
∴的个位数可能是1或6,
观察选项可知,只有B选项为1,
故选B.
8.A
【分析】利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.
【详解】解:∵S1=(AB-a) a+(CD-b)(AD-a)=(AB-a) a+(AB-b)(AD-a),
S2=(AB-a)(AD-b)+(AD-a)(AB-b),
∴S1-S2=(AB-a) a+(AB-b)(AD-a)-(AB-a)(AD-b)-(AD-a)(AB-b)
=(AB-a) a-(AB-a)(AD-b)
=(AB-a) (a-AD+b)
=BE FG,
故选:A.
9.C
【分析】根据题目条件可用x来表示z,并代入代数式中,运用公式法因式分解可得,再根据平方数的非负性可分别求出x,z的值,最后运算即可.
【详解】解: , ,
又 ,
,
,,
,
,
,
代入得,=0.
故选:C.
10.C
【分析】先提取公因式,再根据平方差公式将因式分解,根据题意即可进行解答.
【详解】解:,
当时,,
∴可以产生的密码是:202218,201822,222018,221820,182220,182022;
不能产生的密码是222180,
故选:C.
二.填空题
11.或或或
【分析】根据完全平方公式展开式的首、末两项是平方项,并且首末两项的符号相同;中间项是首末两项的底数的积的2倍,对多项式进行分类讨论,分别求出k即可.
【详解】解:①当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴;
②当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴,解得:;
③当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴,解得:;
故答案为:或或或.
12.
【分析】将x2y2﹣2x2y﹣3xy2利用提公因式法进行因式分解,再除以2xy即得A.
【详解】解:∵x2y2﹣2x2y﹣3xy2,
=xy(xy﹣2x﹣3y),
∴A=xy(xy﹣2x﹣3y)÷2xy,
,
故答案为:.
13.
【分析】根据条件求得,根据幂的乘方公式对进行变形,再整体代入求值即可.
【详解】解:∵,
即
∴,
则
.
故答案为:.
14.
【分析】由已知条件可得,,代入,可得,利用完全平方公式展开,即可求解.
【详解】解: ,,,
,,
,
,
,
整理得:,
,
故答案为:12.
15.
【分析】通过已知条件,找到的关系:,,,即可获得答案.
【详解】解:∵,
∴,
∴,
∴,
∵,
∴,
∴,即,,
∵,
∴,
∴,
∴,
∴
故答案为:.
16.a=2b
【分析】如下图,先求出空白部分的面积,然后求出阴影部分的面积,利用,可得出a、b之间的关系.
【详解】如下图
则空白部分的面积+
化简得:
∵
∴
化简得:=0
∴a=2b
故答案为:a=2b.
三.解答题
17.(1)解:∵
∴
(2)当时
18.(1)解:
;
故答案为:.
(2)解:
故答案为:.
19.解:∵
,
∵与的取值无关,
∴,
解得;
;
当时,
.
20.(1)解:∵,
,
,
,
∴;
故答案为:;
(2)解:∵,
∴a项的系数是;
故答案为:;
(3)解:
.
21.(1)解:设,,
则,,
;
故答案为:;
(2)设,,
则,,
;
(3),,
设,,
,
,
,
图中阴影部分的面积为平方单位.
故答案为:.
22.(1)解:根据题意,计算49:
第一步:49接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
故答案为:25,1,1;
(2)根据山桂娜同学的方法,填写出正确的计算公式如下:
.
故答案为:25,,;
(3)∵,
,
∴公式正确;
(4)
;
(5)计算的口算方法,具体步骤如下:
第一步:;
第二步:;
第三步:前面两步的结果综合起来,的结果是4221.
结合上述计算过程,可书写计算公式为.
故答案为:;
(6)∵
,
又∵
,
∴公式是正确的.
23.(1)①证明:∵是一个四位数,
能被9整除,能被9整除,
四位数能被9整除;
②解: 是一个五位数,
,
五位数能被9整除,
能被9整除,
,
故答案为:1;
(2)解:三位数的各位数字是任意三个连续的正整数,
不妨假设,
,
三位数的最小正因数一定是3,
故答案为:3;
(3)解: 均为0至9之间的整数
由能被1整除,可得为质数,
由四位数能被4整除,可得两位数能被4整除,则,
由九位数中已有7,9,可得,
由五位数能被5整除,可得末尾数字,从而得到,
由八位数能被8整除,可得三位数能被8整除,从而得到,
这时的九位数为:,
对应,
为质数,
,
两位数能被2整除,且,
,
,
这个九位数时:381654729,
故答案为:381654729.
一.选择题(共10小题,满分30分,每小题3分)
1.已知,,则的值为( )
A.9 B.7 C.5 D.3
2.已知,,,,则a、b、c、d的大小关系是( )
A. B. C. D.
3.若的结果中不含项,则a、b满足的数量关系为( )
A. B. C. D.
4.将多项式除以后得商式,余式为0,则的值为( )
A.3 B.23 C.25 D.29
5.已知在中,、为整数,能使这个因式分解过程成立的的值共有( )个
A.4 B.5 C.8 D.10
6.已知,,,则的值为
A.0 B.1 C.2 D.3
7.的个位数字为( )
A.5 B.1 C.2 D.4
8.在矩形内,将两张边长分别为和的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,若图①中阴影部分面积为,图②中阴影部分的面积和为.则的值表示正确的是( )
A. B. C. D.
9.已知满足,,则的值为( )
A.4 B.1 C.0 D.-8
10.有一种用“因式分解”法产生的密码记忆法,方法是:取一个多项式,如:,将此多项式因式分解的结果是:.再取两个值,如:,那么各个因式的值是:,于是就可以把“162130”作为一个六位数密码.如果取多项式以及,那么下列密码不可能是用上述方法产生的是( )
A.221820 B.222018 C.222180 D.201822
二.填空题(共6小题,满分18分,每小题3分)
11.若多项式可化为的形式,则单项式可以是 .
12.已知A是多项式,若,则A= .
13.若,,则用含的代数式表示为 .
14.设,,,若,则的值为 .
15.已知,且互不相等,则 .
16.用4张长为宽为 的长方形纸片,按如图的方式拼成一个边长为的正方形,图中空白部分的面积为,阴影部分的面积为.若,则之间存在的数量关系是 .
三.解答题(共7小题,满分52分)
17.(6分)已知
(1)求的值; (2)求的值.
18.(6分)分解因式:
(1); (2).
19.(8分)已知,,且与的3倍的差的值与的取值无关,求代数式的值.
20.(8分)阅读材料,完成相应任务:“贾宪三角”又称“杨辉三角”,在欧洲则称为“帕斯卡三角”(如图所示),它揭示了(n为非负数)展开式的各项系数的规律.
根据上述规律,完成下列问题:
(1)直接写出_________.
(2)的展开式中a项的系数是__________.
(3)利用上述规律求的值,写出过程.
21.(8分)阅读理解:
若满足,求的值.
解:设,,
则,,
.
解决问题
(1)若满足,则 ;
(2)若满足,求的值;
(3)如图,在长方形中,,,点,是,上的点,且,分别以,为边在长方形外侧作正方形和,若长方形的面积为50平方单位,则图中阴影部分的面积和为 平方单位.
22.(8分)阅读并思考:
计算时,山桂娜同学发现了一个简单的口算方法,具体步骤如下:
第一步:47接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
(1)依此方法计算49:
第一步:49接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
(2)请你根据山桂娜同学的方法,填写出一个正确的计算公式.
.
(3)利用乘法运算说明第(2)小题中这个公式的正确性.
(4)写出利用这个公式计算的过程.
(5)计算也有一个简单的口算方法,具体步骤如下:
第一步:;
第二步:;
第三步:前面两步的结果综合起来,的结果是4221.
写出上述过程所依据的计算公式_______________________.
(6)利用乘法运算说明第(5)小题中这个公式的正确性.
23.(8分)阅读:证明命题“一个三位数各位数字之和可以被3整除,则这个数就可以被3整除”.
设表示一个三位数,
则
因为能被3整除,如果也能被3整除,那么就能被3整除.
(1)①一个四位数,如果能被9整除,证明能被9整除;
②若一个五位数能被9整除,则______;
(2)若一个三位数的各位数字是任意三个连续的正整数,则的最小正因数一定是______(数字“1”除外);
(3)由数字1至9组成的一个九位数,这个数的第一位能被1整除,前两位组成的两位数能被2整除,前三位组成的三位数能被3整除,以此类推,一直到整个九位数能被9整除,写出这个九位数是______.
答案解析
选择题
1.B
【分析】根据幂的乘方的逆运算和同底数幂的乘法的逆运算,求得,即可求解.
【详解】解:由可得
∴
∴
故选:B
2.A
【分析】先变形化简,,,,比较11次幂的底数大小即可.
【详解】因为,,,,
因为,
所以,
所以,
故即;
同理可证
所以,
故选A.
3.C
【分析】原式利用多项式乘多项式法则计算,合并后根据结果不含项,即可求出a与b的值.
【详解】解:
∵不含项,
∴,
∴,
故选:C.
4.D
【分析】先把整式化简,然后由整式的乘法、除法运算进行运算,求出a、b、c的值,即可得到答案.
【详解】解:
=;
∵,
∴,,,
∴,,,
∴;
故选:D.
5.B
【分析】先根据整式的乘法可得,再根据“为整数”进行分析即可得.
【详解】,
,
,
根据为整数,有以下10种情况:
(1)当时,;
(2)当时,;
(3)当时,;
(4)当时,;
(5)当时,;
(6)当时,;
(7)当时,;
(8)当时,;
(9)当时,;
(10)当时,;
综上,符合条件的m的值为,共有5个,
故选:B.
6.D
【分析】根据,,,可以得到,,的值,然后将所求式子变形,再将,,的值代入计算即可.
【详解】解:,,,
,,,
,
故选:D.
7.B
【分析】将变形为,利用平方差公式求解.
【详解】解:
,
∵ ,,,,……
可知个位数变化规律为:3,9,7,1,4次一个循环,
∴的个位数为1,
∴的个位数为0,
∴的个位数可能是0或5,
∴的个位数可能是1或6,
观察选项可知,只有B选项为1,
故选B.
8.A
【分析】利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.
【详解】解:∵S1=(AB-a) a+(CD-b)(AD-a)=(AB-a) a+(AB-b)(AD-a),
S2=(AB-a)(AD-b)+(AD-a)(AB-b),
∴S1-S2=(AB-a) a+(AB-b)(AD-a)-(AB-a)(AD-b)-(AD-a)(AB-b)
=(AB-a) a-(AB-a)(AD-b)
=(AB-a) (a-AD+b)
=BE FG,
故选:A.
9.C
【分析】根据题目条件可用x来表示z,并代入代数式中,运用公式法因式分解可得,再根据平方数的非负性可分别求出x,z的值,最后运算即可.
【详解】解: , ,
又 ,
,
,,
,
,
,
代入得,=0.
故选:C.
10.C
【分析】先提取公因式,再根据平方差公式将因式分解,根据题意即可进行解答.
【详解】解:,
当时,,
∴可以产生的密码是:202218,201822,222018,221820,182220,182022;
不能产生的密码是222180,
故选:C.
二.填空题
11.或或或
【分析】根据完全平方公式展开式的首、末两项是平方项,并且首末两项的符号相同;中间项是首末两项的底数的积的2倍,对多项式进行分类讨论,分别求出k即可.
【详解】解:①当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴;
②当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴,解得:;
③当和作为平方项,作为乘积项,则多项式可化为:
,即,
∴,解得:;
故答案为:或或或.
12.
【分析】将x2y2﹣2x2y﹣3xy2利用提公因式法进行因式分解,再除以2xy即得A.
【详解】解:∵x2y2﹣2x2y﹣3xy2,
=xy(xy﹣2x﹣3y),
∴A=xy(xy﹣2x﹣3y)÷2xy,
,
故答案为:.
13.
【分析】根据条件求得,根据幂的乘方公式对进行变形,再整体代入求值即可.
【详解】解:∵,
即
∴,
则
.
故答案为:.
14.
【分析】由已知条件可得,,代入,可得,利用完全平方公式展开,即可求解.
【详解】解: ,,,
,,
,
,
,
整理得:,
,
故答案为:12.
15.
【分析】通过已知条件,找到的关系:,,,即可获得答案.
【详解】解:∵,
∴,
∴,
∴,
∵,
∴,
∴,即,,
∵,
∴,
∴,
∴,
∴
故答案为:.
16.a=2b
【分析】如下图,先求出空白部分的面积,然后求出阴影部分的面积,利用,可得出a、b之间的关系.
【详解】如下图
则空白部分的面积+
化简得:
∵
∴
化简得:=0
∴a=2b
故答案为:a=2b.
三.解答题
17.(1)解:∵
∴
(2)当时
18.(1)解:
;
故答案为:.
(2)解:
故答案为:.
19.解:∵
,
∵与的取值无关,
∴,
解得;
;
当时,
.
20.(1)解:∵,
,
,
,
∴;
故答案为:;
(2)解:∵,
∴a项的系数是;
故答案为:;
(3)解:
.
21.(1)解:设,,
则,,
;
故答案为:;
(2)设,,
则,,
;
(3),,
设,,
,
,
,
图中阴影部分的面积为平方单位.
故答案为:.
22.(1)解:根据题意,计算49:
第一步:49接近整十数50,;
第二步:取50的一半25,;
第三步:
第四步:把第二、三步综合起来,.
故答案为:25,1,1;
(2)根据山桂娜同学的方法,填写出正确的计算公式如下:
.
故答案为:25,,;
(3)∵,
,
∴公式正确;
(4)
;
(5)计算的口算方法,具体步骤如下:
第一步:;
第二步:;
第三步:前面两步的结果综合起来,的结果是4221.
结合上述计算过程,可书写计算公式为.
故答案为:;
(6)∵
,
又∵
,
∴公式是正确的.
23.(1)①证明:∵是一个四位数,
能被9整除,能被9整除,
四位数能被9整除;
②解: 是一个五位数,
,
五位数能被9整除,
能被9整除,
,
故答案为:1;
(2)解:三位数的各位数字是任意三个连续的正整数,
不妨假设,
,
三位数的最小正因数一定是3,
故答案为:3;
(3)解: 均为0至9之间的整数
由能被1整除,可得为质数,
由四位数能被4整除,可得两位数能被4整除,则,
由九位数中已有7,9,可得,
由五位数能被5整除,可得末尾数字,从而得到,
由八位数能被8整除,可得三位数能被8整除,从而得到,
这时的九位数为:,
对应,
为质数,
,
两位数能被2整除,且,
,
,
这个九位数时:381654729,
故答案为:381654729.
