最新华师版八上数学 14.2 勾股定理的应用 上课课件(共37张PPT)
文档属性
| 名称 | 最新华师版八上数学 14.2 勾股定理的应用 上课课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览






文档简介
(共37张PPT)
华东师大版·八年级上册
勾股定理的应用(1)
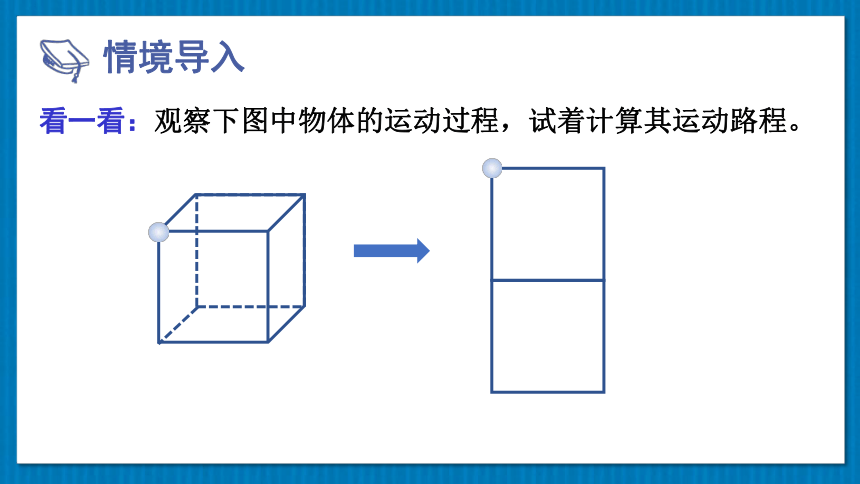
情境导入
看一看:观察下图中物体的运动过程,试着计算其运动路程。
探究新知
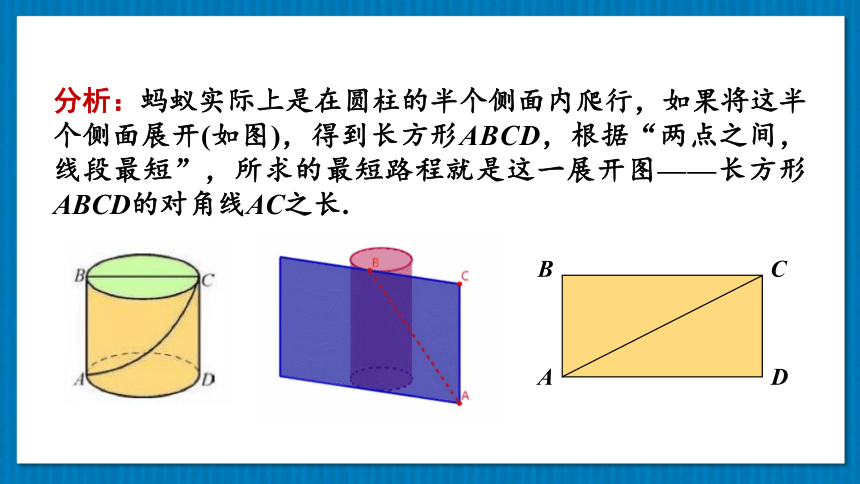
例1
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
试
一
试
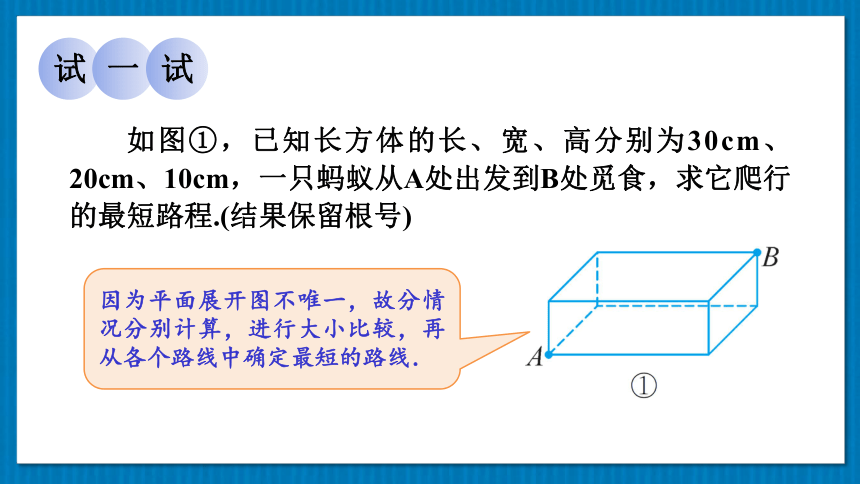
如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
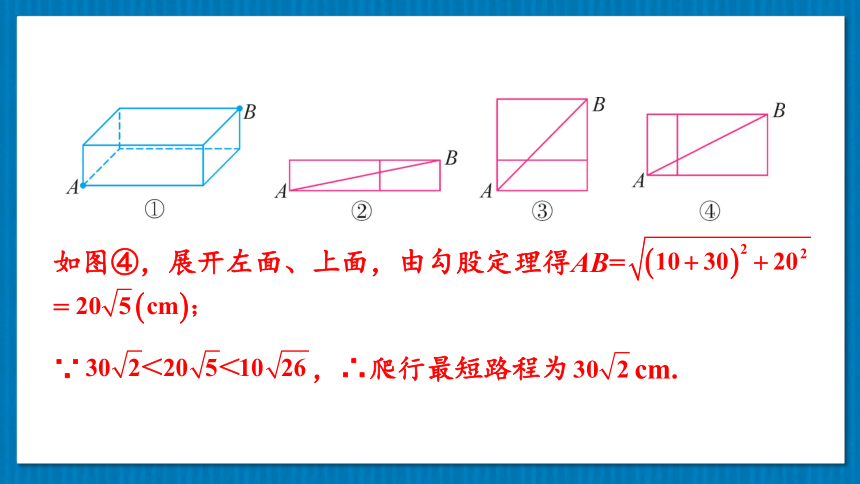
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上.如左图所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的.若将树干的侧面展开成一个平面,如右图所示,可清楚的看出葛藤在这个平面上是沿直线上升的.
例2
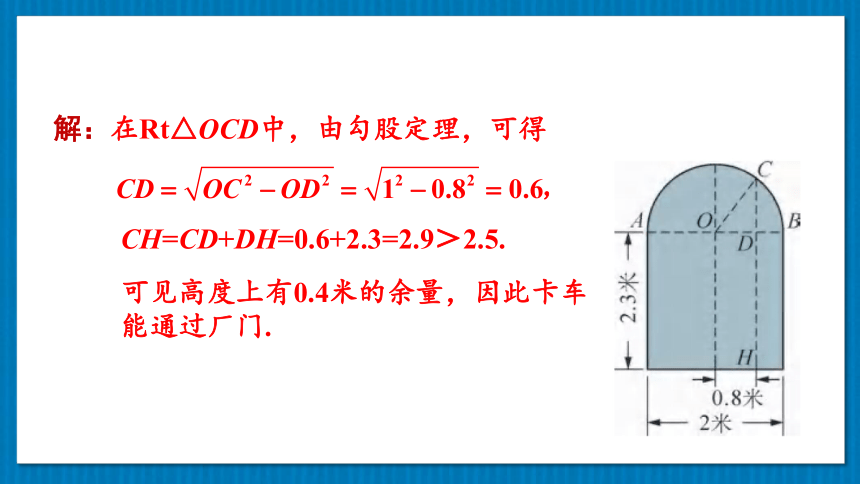
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
试
一
试
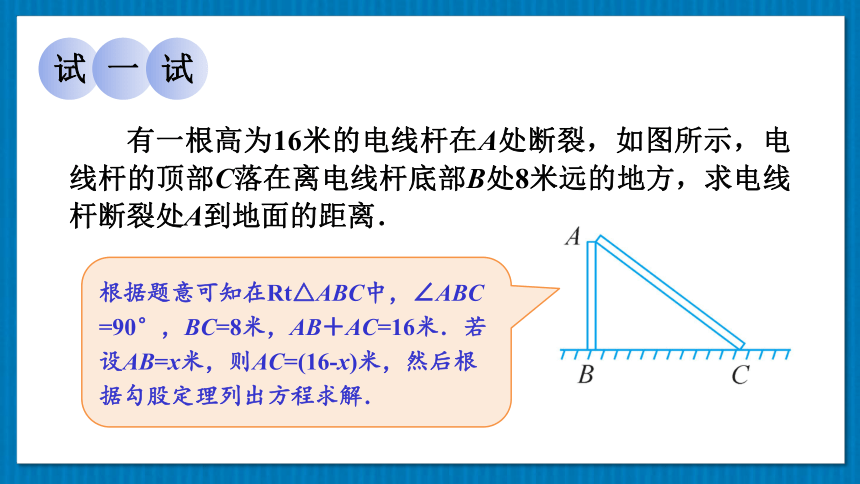
有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
做
一
做
如图所示,以Rt△ABC的三边为边分别向外作正方形.在以BC为边所作的正方形中,点O是正方形对角线的交点,过点O作AB的平行线,交正方形于M、N两点,过点O作MN的垂线,交正方形于E、F两点,这样把正方形划分成四个形状与大小都一样的四边形.试将图中5个着色的图形拼入到上方空白的大正方形中,填满整个大正方形.
点击打开几何画板
随堂练习
1.为了加固电线杆,往往需要给它拉上一条固定于地面的钢缆如图,从电线杆离地面5米处向地面拉一条7米长的钢缆,求钢缆在地面上的固定点A到电线杆底部B的距离. (精确到0.1米)
解:由勾股定理可知AB= (米).
答:钢缆在地面上的固定点A到电线杆底部B的距离约为4.9米.
2.轮船A以16海里/时的速度离开港口O向东北方向航行,轮船B在同时同地以12海里/时的速度向西北方向航行.试求A、B两船离开港口O一个半小时后的距离.
解: (海里).
课堂小结
1.要记住勾股定理及逆定理的内容.
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
勾股定理的应用(2)
复习回顾
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
a
b
c
A
B
C
如果在Rt△ABC中,∠C=90°,
字母表示:
那么a2+b2=c2.
勾股定理逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
a
b
c
A
B
C
字母表示:
如果△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
那么△ABC是直角三角形.
探究新知
例3
如图所示,在3×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2)画出所有以题(1)中所画线段为腰的等腰三角形.
A
分析:只需利用勾股定理看哪一条以格点为端点的线段满足要求.
解:(1)右图中,AB、AC、AE、AD的长度均为 .
A
C
B
E
D
(2)右图中,△ABC、△ABE、△ABD、△ACE、△ACD、△AED就是所要画的等腰三角形.
试
一
试
如图,正方形网格中每一个小正方形的边长都是1,每个小格的顶点叫做格点.请以图中的格点为顶点画一个三角形,使三角形的三边长分别为 .
分析:小正方形的边长为1,由
,得出符合题意的图形.
解:如图,△ABC是所求作的三角形,其中AB= ,BC= ,AC=
.
A
B
C
例4
如图所示,已知CD=6m,AD=8m,∠ADC= 90°,BC=24m,AB=26m.求图中着色部分的面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ABC为直角三角形(勾股定理的逆定理),
∴S阴影部分=S△ACB-S△ACD
试
一
试
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向东南方向航行,乙轮船向西南方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
根据方向角可知两船所走的方向正好
构成了直角,根据勾股定理求出乙轮船航行的路程,进而求出速度.
解:由题意可知,AO⊥BO,OB=20×2=40海里,AB=50海里,
在Rt△AOB中, 海里,
∴乙轮船平均每小时航行30÷2=15海里.
随堂练习
1.形状为直角三角形的一块铁板的三边长分别为2米、4米、x米,试求出x的所有可能值.(精确到0.01米)
解:有两种情况,当斜边长为x米时,x= ≈
4.47;当斜边长为4米时,x= ≈3.46. 所以x约为4.47或3.46.
2.利用勾股定理,分别画出长度为 厘米和 厘米的线段.
解:如图所示,BD= 厘米,如图所示AB= 厘米.
1
1
1
1
2
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a∶b=3∶4,c=15.求a、b.
解:设a=3x,b=4x,在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
4.已知有一块四边形的空地ABCD,如图所示,经测量∠A =90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积.
解:如图,连接BD.
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在Rt△CBD中,CD2=132, BC2=122,
而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
课堂小结
会用勾股定理解决简单应用题,学会构造直角三角形.
A
C
B
E
D
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
勾股定理的应用(1)
情境导入
看一看:观察下图中物体的运动过程,试着计算其运动路程。
探究新知
例1
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
试
一
试
如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上.如左图所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的.若将树干的侧面展开成一个平面,如右图所示,可清楚的看出葛藤在这个平面上是沿直线上升的.
例2
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
试
一
试
有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
做
一
做
如图所示,以Rt△ABC的三边为边分别向外作正方形.在以BC为边所作的正方形中,点O是正方形对角线的交点,过点O作AB的平行线,交正方形于M、N两点,过点O作MN的垂线,交正方形于E、F两点,这样把正方形划分成四个形状与大小都一样的四边形.试将图中5个着色的图形拼入到上方空白的大正方形中,填满整个大正方形.
点击打开几何画板
随堂练习
1.为了加固电线杆,往往需要给它拉上一条固定于地面的钢缆如图,从电线杆离地面5米处向地面拉一条7米长的钢缆,求钢缆在地面上的固定点A到电线杆底部B的距离. (精确到0.1米)
解:由勾股定理可知AB= (米).
答:钢缆在地面上的固定点A到电线杆底部B的距离约为4.9米.
2.轮船A以16海里/时的速度离开港口O向东北方向航行,轮船B在同时同地以12海里/时的速度向西北方向航行.试求A、B两船离开港口O一个半小时后的距离.
解: (海里).
课堂小结
1.要记住勾股定理及逆定理的内容.
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
勾股定理的应用(2)
复习回顾
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
a
b
c
A
B
C
如果在Rt△ABC中,∠C=90°,
字母表示:
那么a2+b2=c2.
勾股定理逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
a
b
c
A
B
C
字母表示:
如果△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
那么△ABC是直角三角形.
探究新知
例3
如图所示,在3×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2)画出所有以题(1)中所画线段为腰的等腰三角形.
A
分析:只需利用勾股定理看哪一条以格点为端点的线段满足要求.
解:(1)右图中,AB、AC、AE、AD的长度均为 .
A
C
B
E
D
(2)右图中,△ABC、△ABE、△ABD、△ACE、△ACD、△AED就是所要画的等腰三角形.
试
一
试
如图,正方形网格中每一个小正方形的边长都是1,每个小格的顶点叫做格点.请以图中的格点为顶点画一个三角形,使三角形的三边长分别为 .
分析:小正方形的边长为1,由
,得出符合题意的图形.
解:如图,△ABC是所求作的三角形,其中AB= ,BC= ,AC=
.
A
B
C
例4
如图所示,已知CD=6m,AD=8m,∠ADC= 90°,BC=24m,AB=26m.求图中着色部分的面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ABC为直角三角形(勾股定理的逆定理),
∴S阴影部分=S△ACB-S△ACD
试
一
试
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向东南方向航行,乙轮船向西南方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
根据方向角可知两船所走的方向正好
构成了直角,根据勾股定理求出乙轮船航行的路程,进而求出速度.
解:由题意可知,AO⊥BO,OB=20×2=40海里,AB=50海里,
在Rt△AOB中, 海里,
∴乙轮船平均每小时航行30÷2=15海里.
随堂练习
1.形状为直角三角形的一块铁板的三边长分别为2米、4米、x米,试求出x的所有可能值.(精确到0.01米)
解:有两种情况,当斜边长为x米时,x= ≈
4.47;当斜边长为4米时,x= ≈3.46. 所以x约为4.47或3.46.
2.利用勾股定理,分别画出长度为 厘米和 厘米的线段.
解:如图所示,BD= 厘米,如图所示AB= 厘米.
1
1
1
1
2
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a∶b=3∶4,c=15.求a、b.
解:设a=3x,b=4x,在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
4.已知有一块四边形的空地ABCD,如图所示,经测量∠A =90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积.
解:如图,连接BD.
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在Rt△CBD中,CD2=132, BC2=122,
而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
课堂小结
会用勾股定理解决简单应用题,学会构造直角三角形.
A
C
B
E
D
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
