六年级下册数学北师大版总复习统计与概率课件(共45张PPT)
文档属性
| 名称 | 六年级下册数学北师大版总复习统计与概率课件(共45张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
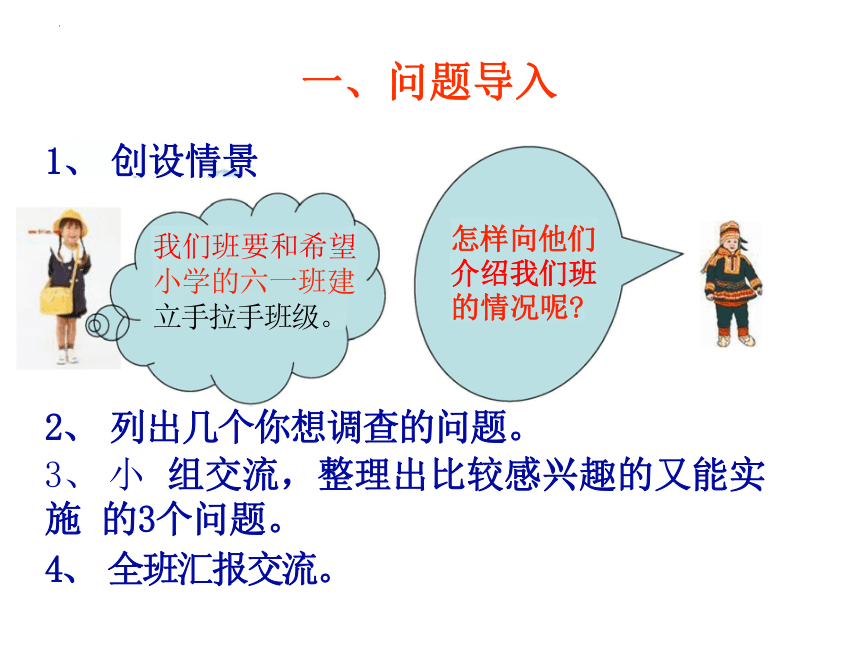
2、 列出几个你想调查的问题。
3、 小 组交流,整理出比较感兴趣的又能实施 的3个问题。
4、 全班汇报交流。
1、 创设情景
我们班要和希望
小学的六一班建
立手拉手班级。
怎样向他们
介绍我们班
的情况呢
一、问题导入
二、回顾统计活动
在刚才的统计活动中,我们都做了些什么 按顺序 说一说。
提出问题——收集数据——整理数据——分析 数据——作出决策
什么是统计
统计是将一组数据进
行收集、整理、计算、 分析的过程。
如何去收集数据。
1、测量
2、实地调查
3、问卷调查
4、直接从报刊、电视、网络获取。
如何去记录数据。
1、画正法
2、画“√ ”法
3、数字记录法
如何去整理数据。
1、分段整理
2、分类整 理
届数 23 24 25 26 27 28
29
枚数 15 5 16 16 28 32
51
第23-29届奥运会中国金牌数统计表
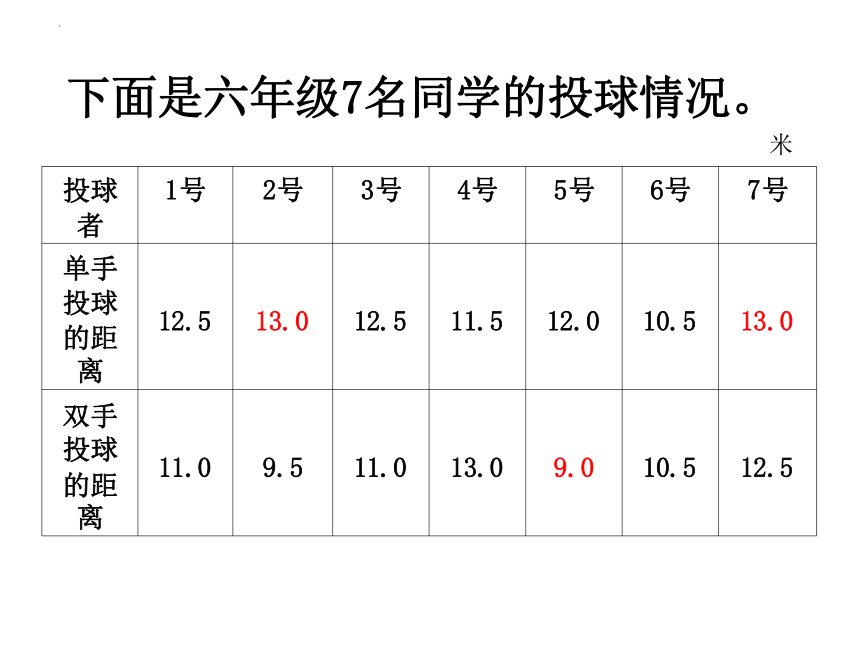
投球 者 1号 2号 3号 4号 5号 6号
7号
单手 投球 的距 离 12.5 13.0 12.5 11.5 12.0 10.5
13.0
双手 投球 的距 离 11.0 9.5 11.0 13.0 9.0 10.5
12.5
下面是六年级7名同学的投球情况。
米
距离/米
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
0
1号 2号 3号 4号 5号 6号 7号 投球者
距离/米
6号 7号 投球者
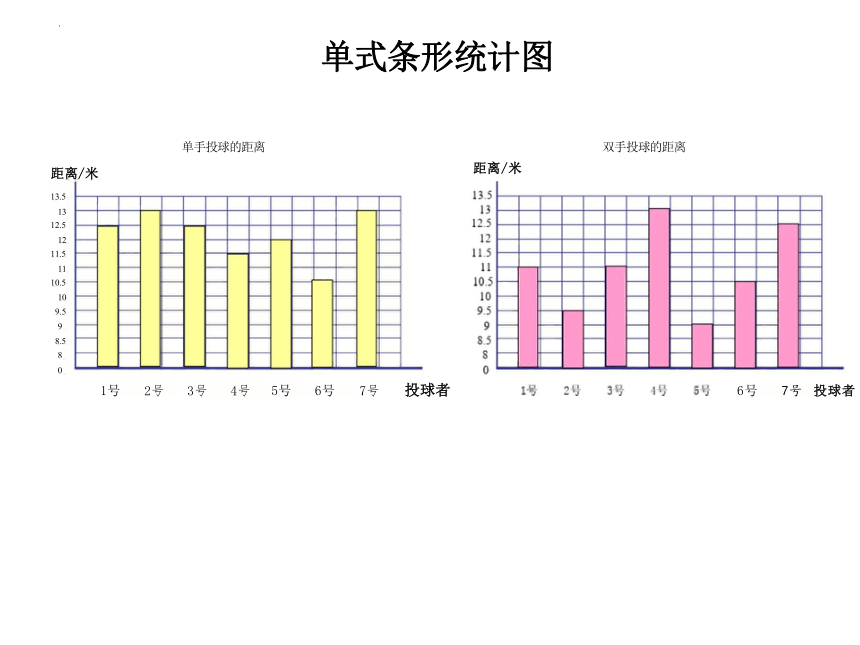
单式条形统计图
单手投球的距离
双手投球的距离
六年级7名同学的投球情况统计图
图例一
合二为一,便于比较
1号 2号 3号 4号 5号 6号 7号 投球者
13.5
13 12.5 12 11.5
11
10.5
10
9.5
9 8.5
8
0
单手投球
双手投球
距离/米
统计表 姓名 三岁 四岁 五岁 六岁 七岁
李宁 98 104 108 114 122 张雪 95 104 110 117 125
李宁3~7岁身高统计图 单位:厘米
122
114
108
104
98
3岁 4 岁 5岁 6 岁 7 岁
张雪3~7岁身高统计图
个单位:厘米 125
117
110
104
95
95
0 3 岁 4 岁 5 岁 6 岁 7 岁
你能把这两 个统计图合 成一个吗
125
120
115
110
105
100
95
0
125
120
115
110
105
100
李宁和张雪3~7岁身高统计图
个单位:厘米
125
122
125
120
115
110
105
100
95
0
3 岁 4 岁 5 岁 6 岁 7 岁
104
98
95
117
114
110
108
—— 李宁
张 雪
104
蔬 菜和水果类
23.7%
谷类47.4%
鱼、禽、肉、
蛋等类
15.8%
奶类和
豆类
11.8%
油脂类1.3%
扇形统计图
定
1、条形统计图
2、折线统计图 3、扇形统计图
我们学过哪些统计图。
单式统计表
复式统计表
条形统计图
折线统计图 扇形统计图
单式条形统计图
复式条形统计图 单式折线统计图 复式折线统计图
整理和描述数据
统计图
统计表
总结:
条形统计图: 能够清楚地看出各部分数
量的多少,便于对比。
折线统计图:不仅能看出各部分数量的 多少,还能看出数量的增减变化的情况。
扇形统计图: 能够清楚地看出部分数量 同总数之间的关系。
选择填空。
A.条形统计图 B.折线统计图 C.扇形统计图
1、表示全校学生课间活动喜欢的游戏的类型分布
情况,应该选择( C )。
2、表示四个同学体重谁轻谁重应该选择( A )。
3、表示5月份气温变化情况应该选择( B )。
填空:
1、 统计数据除了可以分类整理成(统计表)外,还可以制
作 ( 统计图).用统计图表示有关数量之间的关系比统计 表更加( 形象具体 )、使人一目了然,印象深刻。
2、 常用的统计图有( 条形统计图)、( 折线统计图 )
( 扇形统计图 )。
3、条形统计图是用一个(单位长度)表示一定的(数量),
根 据 (数量)的多少画成长短不同的( 直条 ) , 然 后
把这些( 直条 )按照 一 定的( 顺序)排列起来。
4、从条形统计图中很容易看出(各种数量的多少 )。
5、折线统计图是用一个(单位长度 )表示 一定的
( 数量 ) , 根 据 (数量 )的多少描出( 各点) , 然后把( 各点 )用线段连接起来。
6、 折线统计图不但可以表示出(各种数量的多少 ),
而且能够清楚地表示出( 数量增减变化 )的情况 .
7、扇形统计图可以很清楚地表示出( 各部分数量 )
同 ( 总数 )之间的关系。
1、为了能够清楚地表示出2005年月平均气温变化
情况,应绘制(折 线)统计图。
2、从 ( 条 形 )统计图中很容易看出各种数量的
多少。
特大号
小号 7%
9%
大号
30%
中号
54%
李宁服饰商店要对一种运动服的销售情况进行统计,并制作成统计 图,用来确定下一次进货时每种型号进货情况。如果让你来选择, 你会选择哪种统计图。
李宁服饰商店某种运动服的销售 情况条形统计图 2010.5
李宁服饰商店某种运动服的销售 折线情况统计图 2010.5
李宁服饰商店某种运动服的销售 扇形情况统计图 2010.5
年 份 1998 1999 2000 2001 2002
2003
数 量 / 台 15 24 32 45 56
68
北京 天津 上海 杭州 南京
成都
数 量 / 台 68 34 60 45 39
30
1.观察下面的统计表,你获得了哪些信息
2003年部分城市城镇居民
每百户家庭家用电脑拥有量统计表
1998~2003年北京市城镇居民
每百户家庭家用电脑拥有量统计表
这两组数据分别制成什么统计图比较合适 先讨论,再画出来。
2004年6月
2004年6月
平均数
中位数 众 数
常用的
统计量
你知道平均数、中位
数、众数各有什么特点 有什么区别吗
1、什么叫平均数
平均数是指在一组数据中所有数据之和再除以数据
的个数。 平均数是表示一 数 情 况 。 2、什么叫中位数
一组数据按从小到大(或从大到小)的顺序依次排列, 处在中间位置的一个数(或最中间两个数据的平均数)。
中位数是 表示数据的一 般 情 况 。
3、什么叫众数
众数是在一组数据中,出现次数最多的那个数。
众 数能够反映一组数据的集 中情况。
平均数的大小与一组数据里的每个数 据都有关系,任何一个数据的变动都会引 起平均数的变化。
一组数据中只有一个平均数。
用平均数进行统计的特点:
平均数反映整体情况,但容易受偏大 数或偏小数的影响,有时不能真实地反 映一数据的整体情况。
中位数的特点:
中位数反映一组数据的一 般情况,
不受偏大或偏小数的影响。
众数的特点:
能够反映一组数据的集 中情况。众
数与大小无关,与位置无关。
一组数据中如果某个数据出现次数相对较多, 一般选它作为代表。
反映总体平均水平
反映中等水平
反映多数集中水平
一组数据如果比较接近一般选它作为代表。
一组数据如果相差较大一般选它作为代表。
平均数
中位数 众 数
平均数
中位数
众 数
分数 100分 90-99 分 80-89 分 70-79 分 60-69 分
60分
以下
人数 1 3 2 1 2
1
下面是六3班一小组同学在一次考试
中的成绩(单位:分)
64 98 81 53 78 98 100
97 65 86
64 98 81 53 78 98 100
97 65 86
1、这个小组的平均成绩是多少分
(64+98+81+53+78+98+100+97+65+86)÷10
=820÷10
=82(分)
3、如果60分及60分以上为及格,
这小组的及格率是多少
9 ÷10 X 100%=90%
答:这小组的及格率是90%。
分数 100分 90-99 分 80-89 分 70-79 分 60-69 分
6 0 分
以下
人数 1 3 2 1 2
1
员工 经理 王师傅 李师傅 陈师傅
张师傅
月工资(元) 3000 1100 900 800
700
(3000+1100+900+800+700)÷5=1300 (元)
求平均的方法: 总量÷总份数=平均数
员工工资情况
员工 经理 王 师 傅 李 师 傅 陈 师 傅 张师傅
林 师 傅
月工资(元) 3000 1100 900 800 700
680
中位数: (900+800)÷2= 850
员工工资情况
员工 经理 王师傅 李师傅 陈师傅
张师傅
月工资(元) 3000 1100 900 800
400
中位数不受大小数的影响
员工工资情况
偏小
偏大
3000 2000 900 800 750 650 600 600 600 600
500
这组数据的众 数是600。
第 一 组20263020204142333219
这组数据的众数是( 20 )。
第二组20212520332033223319
这组数据的众数是( 2033 )。
第三 组 4 0 4 9 4 0 4 9 5 0 5 5 4 4 5 0 5 5 6 1
这组数据的众数是(40495055 )。
第 四 组 1 2 3 3 2 3 1 3 4 5 4 1 1 7 2 8 1 8 6 6
这组数据的众数是( 没 有
姓名 李明 陈东 刘云 马刚 王朋 张炎
赵丽
成绩/m 36 34 25 34 24 34
34
求出第一组学生掷沙包比赛成绩的平均 数、中位数、众数。
第一小组学生掷沙包比赛成绩单:
小常识
1.平均数的计算要用到所有的数据,它能够充
分利用数据提供的信息,在现实生活中较为常 用。但它受极端值的影响较大。
2.当一组数据中某些数据多次重复出现时,众
数往往是人们关心的一个量,众数不受极端值 的影响,这是它的一个优势。
3.中位数只需很少的计算,不受极端值的影响,
这在有些情况下是一个优点。
选择填空。
A.平均数 B.中位数 C.众数
(1)五年级有两个班,要比较期末考试哪个班的
成绩高一些,应该选取每班成绩的 ( A )。
(2)在一次期中考试中,某班第2小组8名同学的成 绩如下:2、3、86、82、89、92、85、96
用 ( B ) 表示这组同学的成绩水平比较合适。
2,3是极端数据,影响平均数的大小。
(3)在一次期中考试中,某班第4小组7名同学的成
绩如下:90、90、90、90、90、5、100
用 ( B 或C ) 表示这组同学的成绩水平比较合适。
身高/m 1.40 1.43 1.46 1.49 1.52 1.55
1.58
人数 1 3 5 10 12 6
3
体重/kg 30 33 36 39 42 45
48
人数 2 4 5 12 10 4
3
身高:
平均数:(1.4+1.43×3+1.46×5+
1.49×10+1.52×12+1.55×6+
1.58×3)÷40
=60.17÷40
=1.50425(m)
中位数: 就是第20、21名之间的身高。
所以中位数是1.52。
众数: 1.52。
体重:
平均数:
(30×2+33×4+36×5+39×12+42 ×10+45×4+48×3)÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的体重。 所以中位数是39。
众数: 39。
在上面两组数据中,平均数、中位数和众数各是什么
六(7)班同学身高、体重情况如下表:
你去商场买过服装吗 你知道休闲类服
装型号的“均码”是什么意思吗
均码一般是根据人的平均身高、胸围
等数据确定的统一商品型号,与多数人的 型号接近。所以,均码里蕴涵着平均数和 众数的原理。
尺寸:均码
价格:30元
生活中的数学
尺寸:均码
价格:25元
通过这节课的复习,
你有哪些收获
谢谢
2、 列出几个你想调查的问题。
3、 小 组交流,整理出比较感兴趣的又能实施 的3个问题。
4、 全班汇报交流。
1、 创设情景
我们班要和希望
小学的六一班建
立手拉手班级。
怎样向他们
介绍我们班
的情况呢
一、问题导入
二、回顾统计活动
在刚才的统计活动中,我们都做了些什么 按顺序 说一说。
提出问题——收集数据——整理数据——分析 数据——作出决策
什么是统计
统计是将一组数据进
行收集、整理、计算、 分析的过程。
如何去收集数据。
1、测量
2、实地调查
3、问卷调查
4、直接从报刊、电视、网络获取。
如何去记录数据。
1、画正法
2、画“√ ”法
3、数字记录法
如何去整理数据。
1、分段整理
2、分类整 理
届数 23 24 25 26 27 28
29
枚数 15 5 16 16 28 32
51
第23-29届奥运会中国金牌数统计表
投球 者 1号 2号 3号 4号 5号 6号
7号
单手 投球 的距 离 12.5 13.0 12.5 11.5 12.0 10.5
13.0
双手 投球 的距 离 11.0 9.5 11.0 13.0 9.0 10.5
12.5
下面是六年级7名同学的投球情况。
米
距离/米
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
0
1号 2号 3号 4号 5号 6号 7号 投球者
距离/米
6号 7号 投球者
单式条形统计图
单手投球的距离
双手投球的距离
六年级7名同学的投球情况统计图
图例一
合二为一,便于比较
1号 2号 3号 4号 5号 6号 7号 投球者
13.5
13 12.5 12 11.5
11
10.5
10
9.5
9 8.5
8
0
单手投球
双手投球
距离/米
统计表 姓名 三岁 四岁 五岁 六岁 七岁
李宁 98 104 108 114 122 张雪 95 104 110 117 125
李宁3~7岁身高统计图 单位:厘米
122
114
108
104
98
3岁 4 岁 5岁 6 岁 7 岁
张雪3~7岁身高统计图
个单位:厘米 125
117
110
104
95
95
0 3 岁 4 岁 5 岁 6 岁 7 岁
你能把这两 个统计图合 成一个吗
125
120
115
110
105
100
95
0
125
120
115
110
105
100
李宁和张雪3~7岁身高统计图
个单位:厘米
125
122
125
120
115
110
105
100
95
0
3 岁 4 岁 5 岁 6 岁 7 岁
104
98
95
117
114
110
108
—— 李宁
张 雪
104
蔬 菜和水果类
23.7%
谷类47.4%
鱼、禽、肉、
蛋等类
15.8%
奶类和
豆类
11.8%
油脂类1.3%
扇形统计图
定
1、条形统计图
2、折线统计图 3、扇形统计图
我们学过哪些统计图。
单式统计表
复式统计表
条形统计图
折线统计图 扇形统计图
单式条形统计图
复式条形统计图 单式折线统计图 复式折线统计图
整理和描述数据
统计图
统计表
总结:
条形统计图: 能够清楚地看出各部分数
量的多少,便于对比。
折线统计图:不仅能看出各部分数量的 多少,还能看出数量的增减变化的情况。
扇形统计图: 能够清楚地看出部分数量 同总数之间的关系。
选择填空。
A.条形统计图 B.折线统计图 C.扇形统计图
1、表示全校学生课间活动喜欢的游戏的类型分布
情况,应该选择( C )。
2、表示四个同学体重谁轻谁重应该选择( A )。
3、表示5月份气温变化情况应该选择( B )。
填空:
1、 统计数据除了可以分类整理成(统计表)外,还可以制
作 ( 统计图).用统计图表示有关数量之间的关系比统计 表更加( 形象具体 )、使人一目了然,印象深刻。
2、 常用的统计图有( 条形统计图)、( 折线统计图 )
( 扇形统计图 )。
3、条形统计图是用一个(单位长度)表示一定的(数量),
根 据 (数量)的多少画成长短不同的( 直条 ) , 然 后
把这些( 直条 )按照 一 定的( 顺序)排列起来。
4、从条形统计图中很容易看出(各种数量的多少 )。
5、折线统计图是用一个(单位长度 )表示 一定的
( 数量 ) , 根 据 (数量 )的多少描出( 各点) , 然后把( 各点 )用线段连接起来。
6、 折线统计图不但可以表示出(各种数量的多少 ),
而且能够清楚地表示出( 数量增减变化 )的情况 .
7、扇形统计图可以很清楚地表示出( 各部分数量 )
同 ( 总数 )之间的关系。
1、为了能够清楚地表示出2005年月平均气温变化
情况,应绘制(折 线)统计图。
2、从 ( 条 形 )统计图中很容易看出各种数量的
多少。
特大号
小号 7%
9%
大号
30%
中号
54%
李宁服饰商店要对一种运动服的销售情况进行统计,并制作成统计 图,用来确定下一次进货时每种型号进货情况。如果让你来选择, 你会选择哪种统计图。
李宁服饰商店某种运动服的销售 情况条形统计图 2010.5
李宁服饰商店某种运动服的销售 折线情况统计图 2010.5
李宁服饰商店某种运动服的销售 扇形情况统计图 2010.5
年 份 1998 1999 2000 2001 2002
2003
数 量 / 台 15 24 32 45 56
68
北京 天津 上海 杭州 南京
成都
数 量 / 台 68 34 60 45 39
30
1.观察下面的统计表,你获得了哪些信息
2003年部分城市城镇居民
每百户家庭家用电脑拥有量统计表
1998~2003年北京市城镇居民
每百户家庭家用电脑拥有量统计表
这两组数据分别制成什么统计图比较合适 先讨论,再画出来。
2004年6月
2004年6月
平均数
中位数 众 数
常用的
统计量
你知道平均数、中位
数、众数各有什么特点 有什么区别吗
1、什么叫平均数
平均数是指在一组数据中所有数据之和再除以数据
的个数。 平均数是表示一 数 情 况 。 2、什么叫中位数
一组数据按从小到大(或从大到小)的顺序依次排列, 处在中间位置的一个数(或最中间两个数据的平均数)。
中位数是 表示数据的一 般 情 况 。
3、什么叫众数
众数是在一组数据中,出现次数最多的那个数。
众 数能够反映一组数据的集 中情况。
平均数的大小与一组数据里的每个数 据都有关系,任何一个数据的变动都会引 起平均数的变化。
一组数据中只有一个平均数。
用平均数进行统计的特点:
平均数反映整体情况,但容易受偏大 数或偏小数的影响,有时不能真实地反 映一数据的整体情况。
中位数的特点:
中位数反映一组数据的一 般情况,
不受偏大或偏小数的影响。
众数的特点:
能够反映一组数据的集 中情况。众
数与大小无关,与位置无关。
一组数据中如果某个数据出现次数相对较多, 一般选它作为代表。
反映总体平均水平
反映中等水平
反映多数集中水平
一组数据如果比较接近一般选它作为代表。
一组数据如果相差较大一般选它作为代表。
平均数
中位数 众 数
平均数
中位数
众 数
分数 100分 90-99 分 80-89 分 70-79 分 60-69 分
60分
以下
人数 1 3 2 1 2
1
下面是六3班一小组同学在一次考试
中的成绩(单位:分)
64 98 81 53 78 98 100
97 65 86
64 98 81 53 78 98 100
97 65 86
1、这个小组的平均成绩是多少分
(64+98+81+53+78+98+100+97+65+86)÷10
=820÷10
=82(分)
3、如果60分及60分以上为及格,
这小组的及格率是多少
9 ÷10 X 100%=90%
答:这小组的及格率是90%。
分数 100分 90-99 分 80-89 分 70-79 分 60-69 分
6 0 分
以下
人数 1 3 2 1 2
1
员工 经理 王师傅 李师傅 陈师傅
张师傅
月工资(元) 3000 1100 900 800
700
(3000+1100+900+800+700)÷5=1300 (元)
求平均的方法: 总量÷总份数=平均数
员工工资情况
员工 经理 王 师 傅 李 师 傅 陈 师 傅 张师傅
林 师 傅
月工资(元) 3000 1100 900 800 700
680
中位数: (900+800)÷2= 850
员工工资情况
员工 经理 王师傅 李师傅 陈师傅
张师傅
月工资(元) 3000 1100 900 800
400
中位数不受大小数的影响
员工工资情况
偏小
偏大
3000 2000 900 800 750 650 600 600 600 600
500
这组数据的众 数是600。
第 一 组20263020204142333219
这组数据的众数是( 20 )。
第二组20212520332033223319
这组数据的众数是( 2033 )。
第三 组 4 0 4 9 4 0 4 9 5 0 5 5 4 4 5 0 5 5 6 1
这组数据的众数是(40495055 )。
第 四 组 1 2 3 3 2 3 1 3 4 5 4 1 1 7 2 8 1 8 6 6
这组数据的众数是( 没 有
姓名 李明 陈东 刘云 马刚 王朋 张炎
赵丽
成绩/m 36 34 25 34 24 34
34
求出第一组学生掷沙包比赛成绩的平均 数、中位数、众数。
第一小组学生掷沙包比赛成绩单:
小常识
1.平均数的计算要用到所有的数据,它能够充
分利用数据提供的信息,在现实生活中较为常 用。但它受极端值的影响较大。
2.当一组数据中某些数据多次重复出现时,众
数往往是人们关心的一个量,众数不受极端值 的影响,这是它的一个优势。
3.中位数只需很少的计算,不受极端值的影响,
这在有些情况下是一个优点。
选择填空。
A.平均数 B.中位数 C.众数
(1)五年级有两个班,要比较期末考试哪个班的
成绩高一些,应该选取每班成绩的 ( A )。
(2)在一次期中考试中,某班第2小组8名同学的成 绩如下:2、3、86、82、89、92、85、96
用 ( B ) 表示这组同学的成绩水平比较合适。
2,3是极端数据,影响平均数的大小。
(3)在一次期中考试中,某班第4小组7名同学的成
绩如下:90、90、90、90、90、5、100
用 ( B 或C ) 表示这组同学的成绩水平比较合适。
身高/m 1.40 1.43 1.46 1.49 1.52 1.55
1.58
人数 1 3 5 10 12 6
3
体重/kg 30 33 36 39 42 45
48
人数 2 4 5 12 10 4
3
身高:
平均数:(1.4+1.43×3+1.46×5+
1.49×10+1.52×12+1.55×6+
1.58×3)÷40
=60.17÷40
=1.50425(m)
中位数: 就是第20、21名之间的身高。
所以中位数是1.52。
众数: 1.52。
体重:
平均数:
(30×2+33×4+36×5+39×12+42 ×10+45×4+48×3)÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的体重。 所以中位数是39。
众数: 39。
在上面两组数据中,平均数、中位数和众数各是什么
六(7)班同学身高、体重情况如下表:
你去商场买过服装吗 你知道休闲类服
装型号的“均码”是什么意思吗
均码一般是根据人的平均身高、胸围
等数据确定的统一商品型号,与多数人的 型号接近。所以,均码里蕴涵着平均数和 众数的原理。
尺寸:均码
价格:30元
生活中的数学
尺寸:均码
价格:25元
通过这节课的复习,
你有哪些收获
谢谢
