2024学年上海市中考考前信心卷(无答案)
文档属性
| 名称 | 2024学年上海市中考考前信心卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览

文档简介
2024学年上海市中考考前信心卷
(满分:150分 考试时间:40分钟)
一.选择题(共24分)
1.下列是无理数的是( )
A. B. C. D.
2.下列可以更好提现一组数据波动情况的统计图是( )
A.柱状图 B.条形图 C.饼图 D.折线图
3. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
A. B. C. D.2
4.已知四边形中,对角线与相交于点,,下列判断中错误的是( )
A.如果,,那么四边形是矩形
B.如果,,那么四边形是矩形
C.如果,,那么四边形是菱形
D.如果,,那么四边形是菱形
5.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0) B.(4,0) C.(4.﹣2) D.(4,﹣3)
6.小佘同学对“对角线垂直的四边形”进行了探究:如图,在四边形中,,,,,由上述条件,得到了两个结论:①,②.对于结论①、②下列说法正确的是( )
A.①正确、②错误 B.①错误、②正确 C.①、②正确
二.填空题(共48分)
7.2的平方根为______
8.cos57°_____sin33°(选填“>”或“=”或“<”)
9.方程=-x的解为____________
10.在实数范围内因式分解:2x2-3x-6=___________
11.函数y=的定义域为________
12.若正比例函数y=mnx过第二象限,则反比例函数y=的图像在每个象限,y随x的增大而_________(选填“增大”或“减小”)
13.如图,BE, 分别是的两条中线,设,那么向量用向量,表示为 .
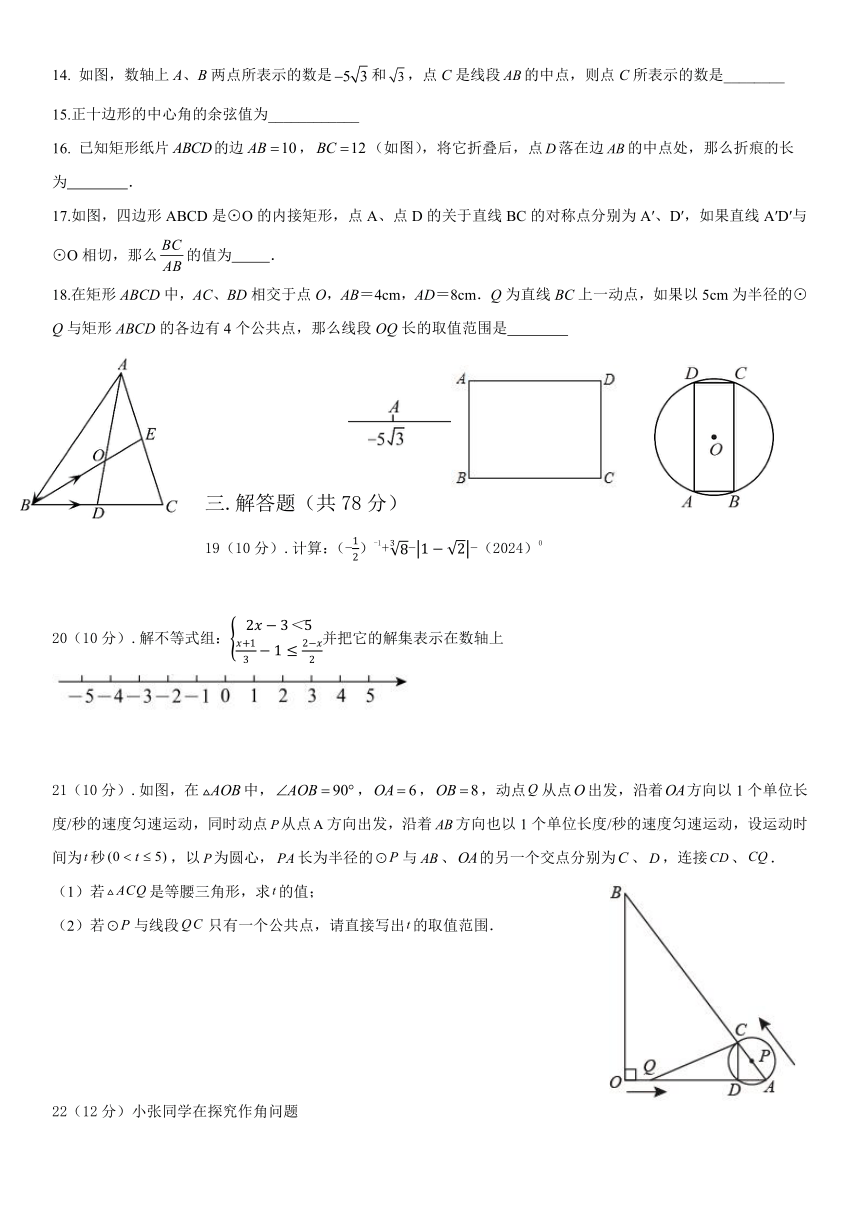
14. 如图,数轴上A、B两点所表示的数是和,点C是线段的中点,则点C所表示的数是________
15.正十边形的中心角的余弦值为____________
16. 已知矩形纸片的边,(如图),将它折叠后,点落在边的中点处,那么折痕的长为 .
17.如图,四边形ABCD是⊙O的内接矩形,点A、点D的关于直线BC的对称点分别为A′、D′,如果直线A′D′与⊙O相切,那么的值为 .
18.在矩形ABCD中,AC、BD相交于点O,AB=4cm,AD=8cm.Q为直线BC上一动点,如果以5cm为半径的⊙Q与矩形ABCD的各边有4个公共点,那么线段OQ长的取值范围是
三.解答题(共78分)
19(10分).计算:(-)-1+--(2024)0
20(10分).解不等式组:并把它的解集表示在数轴上
21(10分).如图,在中,,,,动点从点出发,沿着方向以1个单位长度/秒的速度匀速运动,同时动点从点方向出发,沿着方向也以1个单位长度/秒的速度匀速运动,设运动时间为秒,以为圆心,长为半径的与、的另一个交点分别为、,连接、.
(1)若是等腰三角形,求的值;
(2)若与线段只有一个公共点,请直接写出的取值范围.
22(12分)小张同学在探究作角问题
如果我们身旁没有量角器或三角尺,又需要作,,等大小的角,可以采用如图1的方法:
(1)对折矩形纸片,使与重合,得到折痕,把纸片展平.
(2)再一次折叠纸片,使点A落在上,并使折痕经过点B,得到折痕,同时,得到了线段.
【证明】请根据上述过程完成下列问题:
(1)连接,如图2.请直接写出:______;
(2)请判断和的数量关系,并说明理由;
(3)小张在探究活动的第(2)步基础上再次动手操作(如图3),将延长交于点G.将沿折叠,点B刚好落在边上点H处,连接,把纸片再次展平,求证:四边形是平行四边形.
23(12分). 如图,已知在梯形ABCD中,AD//BC,对角线BD平分∠ABC,点G在底边BC上,联结DG交对角线AC于F,∠DGB=∠DAB.
(1)求证:四边形ABGD是菱形;
(2)联结EG,求证:BG EG=BC EF.
24(12分). 在平面直角坐标系xOy中,我们把以抛物线上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.
25(14分).已知:在半径为2的扇形中,,点C是上的一个动点,直线与直线相交于点D.
(1)如图1,当是等腰三角形时,求的大小(用含m的代数式表示);
(2)如图2,当,点C是的中点时,连接,求的值;
(3)将沿所在的直线折叠,当折叠后的圆弧与所在的直线相切于点,且时,求线段AD的长.
(满分:150分 考试时间:40分钟)
一.选择题(共24分)
1.下列是无理数的是( )
A. B. C. D.
2.下列可以更好提现一组数据波动情况的统计图是( )
A.柱状图 B.条形图 C.饼图 D.折线图
3. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
A. B. C. D.2
4.已知四边形中,对角线与相交于点,,下列判断中错误的是( )
A.如果,,那么四边形是矩形
B.如果,,那么四边形是矩形
C.如果,,那么四边形是菱形
D.如果,,那么四边形是菱形
5.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0) B.(4,0) C.(4.﹣2) D.(4,﹣3)
6.小佘同学对“对角线垂直的四边形”进行了探究:如图,在四边形中,,,,,由上述条件,得到了两个结论:①,②.对于结论①、②下列说法正确的是( )
A.①正确、②错误 B.①错误、②正确 C.①、②正确
二.填空题(共48分)
7.2的平方根为______
8.cos57°_____sin33°(选填“>”或“=”或“<”)
9.方程=-x的解为____________
10.在实数范围内因式分解:2x2-3x-6=___________
11.函数y=的定义域为________
12.若正比例函数y=mnx过第二象限,则反比例函数y=的图像在每个象限,y随x的增大而_________(选填“增大”或“减小”)
13.如图,BE, 分别是的两条中线,设,那么向量用向量,表示为 .
14. 如图,数轴上A、B两点所表示的数是和,点C是线段的中点,则点C所表示的数是________
15.正十边形的中心角的余弦值为____________
16. 已知矩形纸片的边,(如图),将它折叠后,点落在边的中点处,那么折痕的长为 .
17.如图,四边形ABCD是⊙O的内接矩形,点A、点D的关于直线BC的对称点分别为A′、D′,如果直线A′D′与⊙O相切,那么的值为 .
18.在矩形ABCD中,AC、BD相交于点O,AB=4cm,AD=8cm.Q为直线BC上一动点,如果以5cm为半径的⊙Q与矩形ABCD的各边有4个公共点,那么线段OQ长的取值范围是
三.解答题(共78分)
19(10分).计算:(-)-1+--(2024)0
20(10分).解不等式组:并把它的解集表示在数轴上
21(10分).如图,在中,,,,动点从点出发,沿着方向以1个单位长度/秒的速度匀速运动,同时动点从点方向出发,沿着方向也以1个单位长度/秒的速度匀速运动,设运动时间为秒,以为圆心,长为半径的与、的另一个交点分别为、,连接、.
(1)若是等腰三角形,求的值;
(2)若与线段只有一个公共点,请直接写出的取值范围.
22(12分)小张同学在探究作角问题
如果我们身旁没有量角器或三角尺,又需要作,,等大小的角,可以采用如图1的方法:
(1)对折矩形纸片,使与重合,得到折痕,把纸片展平.
(2)再一次折叠纸片,使点A落在上,并使折痕经过点B,得到折痕,同时,得到了线段.
【证明】请根据上述过程完成下列问题:
(1)连接,如图2.请直接写出:______;
(2)请判断和的数量关系,并说明理由;
(3)小张在探究活动的第(2)步基础上再次动手操作(如图3),将延长交于点G.将沿折叠,点B刚好落在边上点H处,连接,把纸片再次展平,求证:四边形是平行四边形.
23(12分). 如图,已知在梯形ABCD中,AD//BC,对角线BD平分∠ABC,点G在底边BC上,联结DG交对角线AC于F,∠DGB=∠DAB.
(1)求证:四边形ABGD是菱形;
(2)联结EG,求证:BG EG=BC EF.
24(12分). 在平面直角坐标系xOy中,我们把以抛物线上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.
25(14分).已知:在半径为2的扇形中,,点C是上的一个动点,直线与直线相交于点D.
(1)如图1,当是等腰三角形时,求的大小(用含m的代数式表示);
(2)如图2,当,点C是的中点时,连接,求的值;
(3)将沿所在的直线折叠,当折叠后的圆弧与所在的直线相切于点,且时,求线段AD的长.
同课章节目录
