2024年广东省初中学业水平考试数学押题卷(3)(含答案)
文档属性
| 名称 | 2024年广东省初中学业水平考试数学押题卷(3)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 14:27:22 | ||
图片预览



文档简介
2024年广东省初中学业水平考试数学押题卷(3)
注意事项:本试卷共4页,23 小题,满分120分,考试用时120分钟.
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名等填写在答题卡上.将条形码粘贴在答题卡“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知a的倒数是2,则a的相反数是
A. -2 C.
2.第19届亚运会于2023年9月在中国杭州成功举办,该届亚运会共征集了118个类别的176家企业,赞助金额超过44亿元.不管是赞助的金额,还是参与的企业数,都已经达到亚运会历史之最.将“44 亿”用科学记数法表示为
3. 如题3图所示, 直线a, b被直线c所截, a∥b, ∠2=∠3, 若∠1=80°, 则∠4等于
A. 20°
B. 40°
C. 60°
D. 80°
4.数学老师要在班上开展项目式学习,他将全班同学分成7个学习小组并采用随机抽签方法确定一个小组进行展示活动,则第4个小组被抽到的概率是
5.下列数值不是不等式组 的整数解的是
A. -2 B. -1 C. 0 D. 1
6.某园林公司准备选购一千株高度大约是2m的某种风景树进行园林装饰,有四个苗圃生产基地投标(单株树的价格都相同).采购小组从四个苗圃中分别任意抽查了20株树苗的高度,得到的数据见题6表:
题6表
苗圃 树苗平均高度(单位: m) 方差
甲苗圃 1.8 0.04
乙苗圃 1.8 0.36
丙苗圃 2.0 0.36
丁苗圃 2.0 0.04
则园林公司应该选择
A. 甲苗圃 B. 乙苗圃 C. 丙苗圃 D. 丁苗圃
7. 如题7图所示,在直角坐标系里,线段AB 两个端点的坐标分别是A(6,6),B(8,2),以原点O为位似中心,在第一象限内将AB 缩小为原来的 后得到线段CD,则线段CD 的长为
A. 2 B. C. 3 D.
8. 关于二次函数. 以下说法错误的是
A. 开口向上 B. 对称轴为直线x= -3
C. 有最小值-1 D. 与y轴交点为(0, 8)
9. 如题9图所示,一种活动衣帽架由三个相同菱形组成,调整菱形的内角A,可使衣帽架拉伸或收缩. 若菱形的边长为10 cm, ∠A=90°, 则AD的长为
A. 30cm B. 40 cm
10. 如题10图所示, 在△ABC中, ∠ACB=90°, 以点B为圆心, BC长为半径画弧,交线段AB于点 D; 以点A 为圆心,AD 长为半径画弧,交线段AC 于点 E. 若AE=2EC, 则
A. C.
二、填空题:本大题共5小题,每小题3分,共15分.
11. 计算:
12. 若 则
13. 若 则以a,b,c为边长的三角形的形状是 .
14. 如题14图所示, 已知正方形ABCD 的边长为2, 以点B为圆心,对角线BD 的长为半径画弧,交 BC的延长线于点 E, 连接DE, 则tan∠BDE= .
15. 如题15图所示, Rt△ABC 中, ∠ACB =90°, AC=8, BC=6, 点O 在AC 上, 且⊙O 分别切BC, AB于点 C,点 D,则阴影部分的面积为 .
三、解答题(一):本大题共3小题,每小题8分,共24分.
16. 先化简,再求值: 其中
17.每年5—7月份,某商家都会在线上平台开设的网店销售荔枝和龙眼两种水果.题17表是5月份某个星期两种水果的销售信息(荔枝2kg/箱,龙眼2.5kg/箱).
题17表
商品 荔枝 龙眼
成本/(元/箱) 30 40
售价/(元/箱) 48 60
这个星期网店销售荔枝和龙眼共1150kg,获利9600元,求这个星期网店销售荔枝和龙眼各多少箱.
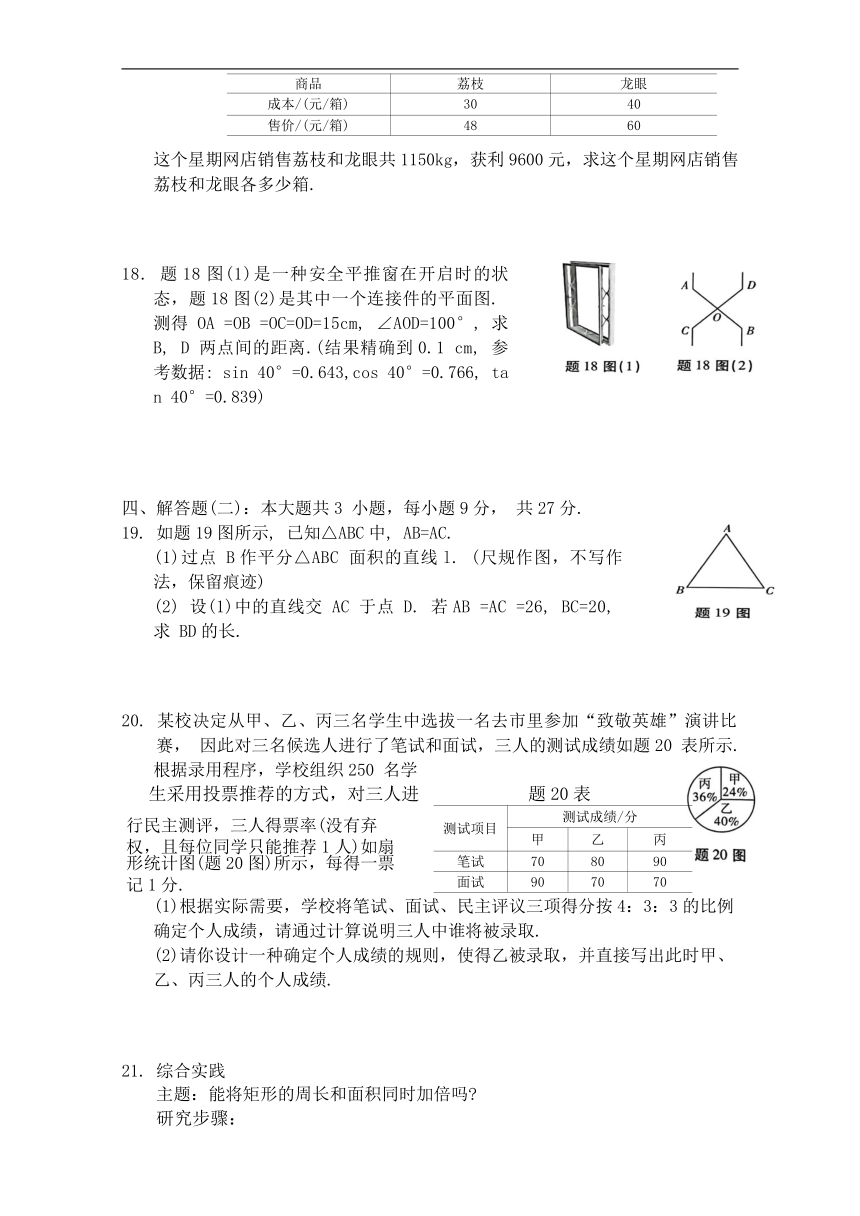
18. 题18图(1)是一种安全平推窗在开启时的状态,题18图(2)是其中一个连接件的平面图. 测得 OA =OB =OC=OD=15cm, ∠AOD=100°, 求B, D 两点间的距离.(结果精确到0.1 cm, 参考数据: sin 40°=0.643,cos 40°=0.766, tan 40°=0.839)
四、解答题(二):本大题共3 小题,每小题9分, 共27分.
19. 如题19图所示, 已知△ABC中, AB=AC.
(1)过点 B作平分△ABC 面积的直线l. (尺规作图,不写作法,保留痕迹)
(2) 设(1)中的直线交 AC 于点 D. 若AB =AC =26, BC=20, 求 BD的长.
20. 某校决定从甲、乙、丙三名学生中选拔一名去市里参加“致敬英雄”演讲比赛, 因此对三名候选人进行了笔试和面试,三人的测试成绩如题20 表所示.
根据录用程序,学校组织250 名学
生采用投票推荐的方式,对三人进 题20表
测试项目 测试成绩/分
甲 乙 丙
笔试 70 80 90
面试 90 70 70
(1)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,请通过计算说明三人中谁将被录取.
(2)请你设计一种确定个人成绩的规则,使得乙被录取,并直接写出此时甲、乙、丙三人的个人成绩.
21. 综合实践
主题:能将矩形的周长和面积同时加倍吗
研究步骤:
(1)特殊化:研究正方形是否能周长和面积同时加倍;
(2)特殊化:研究一个具体的矩形是否能周长和面积同时加倍;
(3)一般化:研究边长比满足什么条件时,矩形的周长和面积可以同时加倍.
操作与计算:
(1) 在题21图中画出将正方形ABCD 周长加倍的正方形 EFGH 和将正方形 ABCD面积加倍的正方形 MNPQ.
(2)对于两边长分别为1 和2的矩形,是否能让周长和面积同时加倍 请通过计算加以说明.
(3)矩形边长比k满足什么条件时,矩形的周长和面积可以同时加倍 请直接写出答案.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22. 综合运用
对于平面直角坐标系xOy中点P(x , y ), Q(x , y )和图形 W,给出如下定义:过点P,Q都分别作x轴和y轴的垂线,四线的另两个交点分别为M,N. 若图形 W中的任意一点 R(a, b) 满足 且 则称四边形 PMQN 是图形 W的一个覆盖,称P,Q为图形 W的覆盖点. 若:x , y 取满足条件的最大值, x , y 取满足条件的最小值,此时称P, Q 为图形 W的最小覆盖点. 例: 已知A(-1,2),B(3, -2), 则点(-1, -2), (3 ,2)为线段AB 的最小覆盖点.
(1) 已知点A(-1, 2), 点B(3, -2), 点 C(2,3).
①△ABC的最小覆盖点为 .
②若△ABC的其中一个覆盖点在直线y=mx+5(m≠0)上, 求m的取值范围.
(2)以点D(2,4)为圆心,半径为3作圆,⊙D的最小覆盖点均在抛物线 上,求该抛物线的顶点坐标.
23. 综合探究
已知在矩形ABCD中, 过点 C 作对角线AC 的垂线l,点 E 为直线BC上一点, 过点 E 作EF⊥AE, 交直线l于点 F.
(1) 如题23图(1)所示, 当点 F 在AD 的延长线上时,
(2) 如题23图(2)所示, 过点 F 作FG⊥BC的延长线, 垂足为点 G, 请写出BE与CG 的数量关系,并说明理由.
(3) 连接DF, 当△ADF是等腰三角形时, 求BE的长.
参考答案:
一、选择题:本大题共10小题,每小题3分,共30分.
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C A D D B C D
二、填空题:本大题共5小题,每小题3分,共15分.
等腰直角三角形
三、解答题(一):本大题共3 小题,每小题8分,共24分.
16.解: 原式 (2分)
(3分)
(4分)
……………………………………………(5分)
当 时,
(8分)
17.解:设这个星期网店销售荔枝x箱,龙眼y箱,依题意得…………………(1分)
(5分)
解得: ………(7分)
答:这个星期网店销售荔枝200箱,龙眼300箱.………………………………(8分)
18.解:连接BD,过点O作OH⊥BD,垂足为点H,见答题18图.
…………………………………………………………………………(1分)
∠BOD=180° -∠AOD=80° .
∵OB=OD, OH⊥BD,
··(3分)
在 Rt△BOH 中,
BHI = OB·sin∠BOH = 15·sin40°= 15×0.643= 9.645(cm)),…(5分)
∴BD=2BH=19.29(cm)≈19.3(cm).……………………………………………(7分)
答:B,D两点间的距离为19.3cm.………………………………………………(8分)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19. 解:(1)见答题19图(1), 直线l为所求作的直线.
…………………………………………………………………(3
分)
(2)过点A 作AE⊥BC, 垂足为点 E, 过点 D 作 DF⊥BC, 垂足为点 F, 见答题19 图(2).
∵AB=AC, AE⊥BC,
…………………(4分)
在 Rt△ACE中, ………………(5分)
. BD 十万△ABC 曲快,
∴点 D 为AC 的中点, 即
在 Rt△CDF 中,
··(7分)
在Rt△BDF 甲, BF=BC-CF=20-5=15,
··(9分)
20. 解:
(1)民主评议:
甲为250×24% =60(分), 乙为250×40% =100(分), 丙为250×36% =90(分).
(3分)
分),
(分),
分).…(6分)
.丙将被录取.…(7分)
(2)若笔试、面试、民主评议三项得分按1:1:2的比例确定个人成绩,乙被录取.此时甲的个人得分为70分,乙的个人得分为87.5分,丙的个人得分为85分.(答案不唯一,请酌情给分)…………………………
(9分)
21.解:(1)答题21图为所求作图形.…………(2分)
(2)能让周长和面积同时加倍,理由如下:……(3分)
设周长加倍后的矩形,较长的一条边长为x,…………
………………………………………………(4分)
若面积也同时加倍,则x(6-x)=4.…………(5分)
解得 舍去x ).…
…………(6分)
∴当较长边为2,较短边为1时矩形的周长和面积能同时加倍.……………(7分)
(3)当k>0时,矩形的周长和面积可以同时加倍.……………………………(9分)
(答k为任何数不扣分)
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.解:(1)①(-1 , -2),(3 ,3). ……(2分)
②由题意得, △ABC的覆盖点见答题22 图(1),当左下方覆盖点在直线y=mx+5 上时,分情况如下:
a. 当y=-2时, mx= -7,
∵x≤-1,m随x增大而增大,
∴0b. 当x=-1时, y= -m+5,
∵y≤-2,
∴m≥7.
综上可得,当左下方覆盖点在直线 y =mx+5 上时,m>0.…………………………………………(4分)
当右上方覆盖点在直线y=mx+5 上时,分情况如下:
a. 当y=3时, mx= -2,
∵x≥3, m随x增大而增大,
b. 当x=3时, y=3m+5,
∵y≥3,
综上可得,当右上方覆盖点在直线y=mx+5上时, (6分)
因此,当 时,△ABC的其中一个覆盖点在直线y=mx+5(m≠0)上.…
(2)由题意得⊙D的最小覆盖点为(-1,1),(5,7), 见答题22图(2).
·(8分)
代入y = x +bx + c, 得解得(10分)
∴该抛物线顶点坐标为 (12分)
23.解:(1)30°.………… ……………(2分)
(2)BE=CG,理由如下:……………………………(3分)
见答题23 图(1), 过点 E 作 EM∥AC.
∵EF⊥AE,
∴ ∠AEF=90° .
· /PAF / FFC
∴∠ACB=30° .
∵AC⊥l,
∴∠ACF=90° .
∵EM∥AC,
∴∠AME =∠MEB+∠B=120°
EC / EC H …(6分)
∴BE =CG. 丷月,
(3)设BE=CG=x.
∵AC⊥l, AC >AD,
∴AF>AD.
若△ADF是等腰三角形,则DF=DA或FA=FD.
(8分)
①如答题23图(2)所示, 当 DF =DA, 且点 F 位于AD上方时, 作DH⊥FG,
在△DFH中, 可得
解得
舍去).
②如答题23图(3)所示, 当DF =DA, 且点 F 位于AD 下方时, 延长 FG交AD 于点 N,
在△DNF 中, 可得
解得
(舍去).
③如答题23 图(4)所示, 当FA=FD 时, 延长FG交AD 于点N,
∵FA=FD, FN⊥AD,
一
综上可得, j …
注意事项:本试卷共4页,23 小题,满分120分,考试用时120分钟.
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名等填写在答题卡上.将条形码粘贴在答题卡“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知a的倒数是2,则a的相反数是
A. -2 C.
2.第19届亚运会于2023年9月在中国杭州成功举办,该届亚运会共征集了118个类别的176家企业,赞助金额超过44亿元.不管是赞助的金额,还是参与的企业数,都已经达到亚运会历史之最.将“44 亿”用科学记数法表示为
3. 如题3图所示, 直线a, b被直线c所截, a∥b, ∠2=∠3, 若∠1=80°, 则∠4等于
A. 20°
B. 40°
C. 60°
D. 80°
4.数学老师要在班上开展项目式学习,他将全班同学分成7个学习小组并采用随机抽签方法确定一个小组进行展示活动,则第4个小组被抽到的概率是
5.下列数值不是不等式组 的整数解的是
A. -2 B. -1 C. 0 D. 1
6.某园林公司准备选购一千株高度大约是2m的某种风景树进行园林装饰,有四个苗圃生产基地投标(单株树的价格都相同).采购小组从四个苗圃中分别任意抽查了20株树苗的高度,得到的数据见题6表:
题6表
苗圃 树苗平均高度(单位: m) 方差
甲苗圃 1.8 0.04
乙苗圃 1.8 0.36
丙苗圃 2.0 0.36
丁苗圃 2.0 0.04
则园林公司应该选择
A. 甲苗圃 B. 乙苗圃 C. 丙苗圃 D. 丁苗圃
7. 如题7图所示,在直角坐标系里,线段AB 两个端点的坐标分别是A(6,6),B(8,2),以原点O为位似中心,在第一象限内将AB 缩小为原来的 后得到线段CD,则线段CD 的长为
A. 2 B. C. 3 D.
8. 关于二次函数. 以下说法错误的是
A. 开口向上 B. 对称轴为直线x= -3
C. 有最小值-1 D. 与y轴交点为(0, 8)
9. 如题9图所示,一种活动衣帽架由三个相同菱形组成,调整菱形的内角A,可使衣帽架拉伸或收缩. 若菱形的边长为10 cm, ∠A=90°, 则AD的长为
A. 30cm B. 40 cm
10. 如题10图所示, 在△ABC中, ∠ACB=90°, 以点B为圆心, BC长为半径画弧,交线段AB于点 D; 以点A 为圆心,AD 长为半径画弧,交线段AC 于点 E. 若AE=2EC, 则
A. C.
二、填空题:本大题共5小题,每小题3分,共15分.
11. 计算:
12. 若 则
13. 若 则以a,b,c为边长的三角形的形状是 .
14. 如题14图所示, 已知正方形ABCD 的边长为2, 以点B为圆心,对角线BD 的长为半径画弧,交 BC的延长线于点 E, 连接DE, 则tan∠BDE= .
15. 如题15图所示, Rt△ABC 中, ∠ACB =90°, AC=8, BC=6, 点O 在AC 上, 且⊙O 分别切BC, AB于点 C,点 D,则阴影部分的面积为 .
三、解答题(一):本大题共3小题,每小题8分,共24分.
16. 先化简,再求值: 其中
17.每年5—7月份,某商家都会在线上平台开设的网店销售荔枝和龙眼两种水果.题17表是5月份某个星期两种水果的销售信息(荔枝2kg/箱,龙眼2.5kg/箱).
题17表
商品 荔枝 龙眼
成本/(元/箱) 30 40
售价/(元/箱) 48 60
这个星期网店销售荔枝和龙眼共1150kg,获利9600元,求这个星期网店销售荔枝和龙眼各多少箱.
18. 题18图(1)是一种安全平推窗在开启时的状态,题18图(2)是其中一个连接件的平面图. 测得 OA =OB =OC=OD=15cm, ∠AOD=100°, 求B, D 两点间的距离.(结果精确到0.1 cm, 参考数据: sin 40°=0.643,cos 40°=0.766, tan 40°=0.839)
四、解答题(二):本大题共3 小题,每小题9分, 共27分.
19. 如题19图所示, 已知△ABC中, AB=AC.
(1)过点 B作平分△ABC 面积的直线l. (尺规作图,不写作法,保留痕迹)
(2) 设(1)中的直线交 AC 于点 D. 若AB =AC =26, BC=20, 求 BD的长.
20. 某校决定从甲、乙、丙三名学生中选拔一名去市里参加“致敬英雄”演讲比赛, 因此对三名候选人进行了笔试和面试,三人的测试成绩如题20 表所示.
根据录用程序,学校组织250 名学
生采用投票推荐的方式,对三人进 题20表
测试项目 测试成绩/分
甲 乙 丙
笔试 70 80 90
面试 90 70 70
(1)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,请通过计算说明三人中谁将被录取.
(2)请你设计一种确定个人成绩的规则,使得乙被录取,并直接写出此时甲、乙、丙三人的个人成绩.
21. 综合实践
主题:能将矩形的周长和面积同时加倍吗
研究步骤:
(1)特殊化:研究正方形是否能周长和面积同时加倍;
(2)特殊化:研究一个具体的矩形是否能周长和面积同时加倍;
(3)一般化:研究边长比满足什么条件时,矩形的周长和面积可以同时加倍.
操作与计算:
(1) 在题21图中画出将正方形ABCD 周长加倍的正方形 EFGH 和将正方形 ABCD面积加倍的正方形 MNPQ.
(2)对于两边长分别为1 和2的矩形,是否能让周长和面积同时加倍 请通过计算加以说明.
(3)矩形边长比k满足什么条件时,矩形的周长和面积可以同时加倍 请直接写出答案.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22. 综合运用
对于平面直角坐标系xOy中点P(x , y ), Q(x , y )和图形 W,给出如下定义:过点P,Q都分别作x轴和y轴的垂线,四线的另两个交点分别为M,N. 若图形 W中的任意一点 R(a, b) 满足 且 则称四边形 PMQN 是图形 W的一个覆盖,称P,Q为图形 W的覆盖点. 若:x , y 取满足条件的最大值, x , y 取满足条件的最小值,此时称P, Q 为图形 W的最小覆盖点. 例: 已知A(-1,2),B(3, -2), 则点(-1, -2), (3 ,2)为线段AB 的最小覆盖点.
(1) 已知点A(-1, 2), 点B(3, -2), 点 C(2,3).
①△ABC的最小覆盖点为 .
②若△ABC的其中一个覆盖点在直线y=mx+5(m≠0)上, 求m的取值范围.
(2)以点D(2,4)为圆心,半径为3作圆,⊙D的最小覆盖点均在抛物线 上,求该抛物线的顶点坐标.
23. 综合探究
已知在矩形ABCD中, 过点 C 作对角线AC 的垂线l,点 E 为直线BC上一点, 过点 E 作EF⊥AE, 交直线l于点 F.
(1) 如题23图(1)所示, 当点 F 在AD 的延长线上时,
(2) 如题23图(2)所示, 过点 F 作FG⊥BC的延长线, 垂足为点 G, 请写出BE与CG 的数量关系,并说明理由.
(3) 连接DF, 当△ADF是等腰三角形时, 求BE的长.
参考答案:
一、选择题:本大题共10小题,每小题3分,共30分.
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C A D D B C D
二、填空题:本大题共5小题,每小题3分,共15分.
等腰直角三角形
三、解答题(一):本大题共3 小题,每小题8分,共24分.
16.解: 原式 (2分)
(3分)
(4分)
……………………………………………(5分)
当 时,
(8分)
17.解:设这个星期网店销售荔枝x箱,龙眼y箱,依题意得…………………(1分)
(5分)
解得: ………(7分)
答:这个星期网店销售荔枝200箱,龙眼300箱.………………………………(8分)
18.解:连接BD,过点O作OH⊥BD,垂足为点H,见答题18图.
…………………………………………………………………………(1分)
∠BOD=180° -∠AOD=80° .
∵OB=OD, OH⊥BD,
··(3分)
在 Rt△BOH 中,
BHI = OB·sin∠BOH = 15·sin40°= 15×0.643= 9.645(cm)),…(5分)
∴BD=2BH=19.29(cm)≈19.3(cm).……………………………………………(7分)
答:B,D两点间的距离为19.3cm.………………………………………………(8分)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19. 解:(1)见答题19图(1), 直线l为所求作的直线.
…………………………………………………………………(3
分)
(2)过点A 作AE⊥BC, 垂足为点 E, 过点 D 作 DF⊥BC, 垂足为点 F, 见答题19 图(2).
∵AB=AC, AE⊥BC,
…………………(4分)
在 Rt△ACE中, ………………(5分)
. BD 十万△ABC 曲快,
∴点 D 为AC 的中点, 即
在 Rt△CDF 中,
··(7分)
在Rt△BDF 甲, BF=BC-CF=20-5=15,
··(9分)
20. 解:
(1)民主评议:
甲为250×24% =60(分), 乙为250×40% =100(分), 丙为250×36% =90(分).
(3分)
分),
(分),
分).…(6分)
.丙将被录取.…(7分)
(2)若笔试、面试、民主评议三项得分按1:1:2的比例确定个人成绩,乙被录取.此时甲的个人得分为70分,乙的个人得分为87.5分,丙的个人得分为85分.(答案不唯一,请酌情给分)…………………………
(9分)
21.解:(1)答题21图为所求作图形.…………(2分)
(2)能让周长和面积同时加倍,理由如下:……(3分)
设周长加倍后的矩形,较长的一条边长为x,…………
………………………………………………(4分)
若面积也同时加倍,则x(6-x)=4.…………(5分)
解得 舍去x ).…
…………(6分)
∴当较长边为2,较短边为1时矩形的周长和面积能同时加倍.……………(7分)
(3)当k>0时,矩形的周长和面积可以同时加倍.……………………………(9分)
(答k为任何数不扣分)
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.解:(1)①(-1 , -2),(3 ,3). ……(2分)
②由题意得, △ABC的覆盖点见答题22 图(1),当左下方覆盖点在直线y=mx+5 上时,分情况如下:
a. 当y=-2时, mx= -7,
∵x≤-1,m随x增大而增大,
∴0
∵y≤-2,
∴m≥7.
综上可得,当左下方覆盖点在直线 y =mx+5 上时,m>0.…………………………………………(4分)
当右上方覆盖点在直线y=mx+5 上时,分情况如下:
a. 当y=3时, mx= -2,
∵x≥3, m随x增大而增大,
b. 当x=3时, y=3m+5,
∵y≥3,
综上可得,当右上方覆盖点在直线y=mx+5上时, (6分)
因此,当 时,△ABC的其中一个覆盖点在直线y=mx+5(m≠0)上.…
(2)由题意得⊙D的最小覆盖点为(-1,1),(5,7), 见答题22图(2).
·(8分)
代入y = x +bx + c, 得解得(10分)
∴该抛物线顶点坐标为 (12分)
23.解:(1)30°.………… ……………(2分)
(2)BE=CG,理由如下:……………………………(3分)
见答题23 图(1), 过点 E 作 EM∥AC.
∵EF⊥AE,
∴ ∠AEF=90° .
· /PAF / FFC
∴∠ACB=30° .
∵AC⊥l,
∴∠ACF=90° .
∵EM∥AC,
∴∠AME =∠MEB+∠B=120°
EC / EC H …(6分)
∴BE =CG. 丷月,
(3)设BE=CG=x.
∵AC⊥l, AC >AD,
∴AF>AD.
若△ADF是等腰三角形,则DF=DA或FA=FD.
(8分)
①如答题23图(2)所示, 当 DF =DA, 且点 F 位于AD上方时, 作DH⊥FG,
在△DFH中, 可得
解得
舍去).
②如答题23图(3)所示, 当DF =DA, 且点 F 位于AD 下方时, 延长 FG交AD 于点 N,
在△DNF 中, 可得
解得
(舍去).
③如答题23 图(4)所示, 当FA=FD 时, 延长FG交AD 于点N,
∵FA=FD, FN⊥AD,
一
综上可得, j …
同课章节目录
