【沪科版九上同步练习】 22.3 相似三角形的性质(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 22.3 相似三角形的性质(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】 22.3相似三角形的性质
一、填空题
1.如图,在 中, , ,垂足为 , ,则 的长为 .
2.如图,△ABC中,点D、E分别是AB、AC的中点,若S△ADE=2,则S△ABC= .
3.已知 ∽ ,AB: :5,那么 : .
4.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
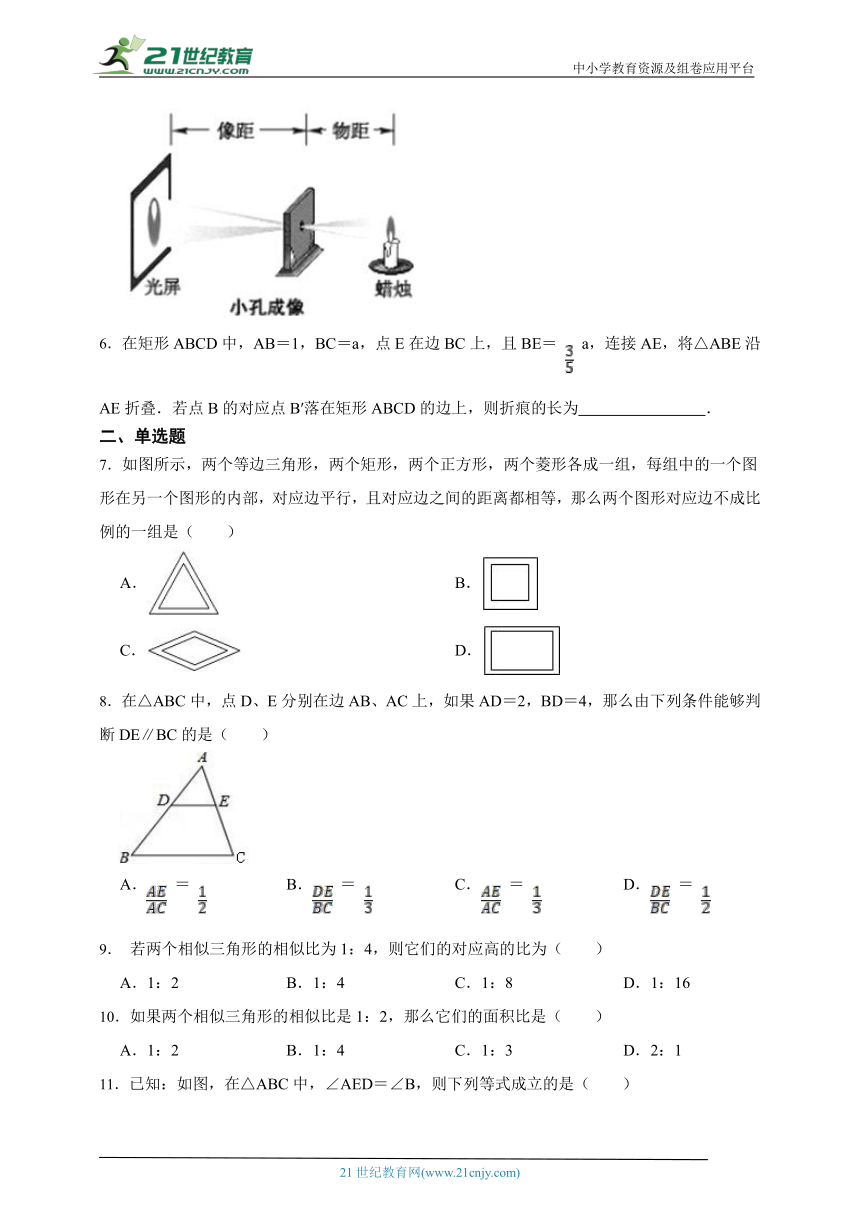
5.两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20cm,光屏在距小孔30cm处,小华测量了蜡烛的火焰高度为2cm,则光屏上火焰所成像的高度为 cm.
6.在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE= a,连接AE,将△ABE沿AE折叠.若点B的对应点B′落在矩形ABCD的边上,则折痕的长为 .
二、单选题
7.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形对应边不成比例的一组是( )
A. B.
C. D.
8.在△ABC中,点D、E分别在边AB、AC上,如果AD=2,BD=4,那么由下列条件能够判断DE∥BC的是( )
A. = B. = C. = D. =
9. 若两个相似三角形的相似比为1:4,则它们的对应高的比为( )
A.1:2 B.1:4 C.1:8 D.1:16
10.如果两个相似三角形的相似比是1:2,那么它们的面积比是( )
A.1:2 B.1:4 C.1:3 D.2:1
11.已知:如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A. B. C. D.
三、解答题
12.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=6,BD=3,求CD的长.
13.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高,于是,两人在灯下沿直线移动,如图,当小聪正好站在广场的点(距点5块地砖长)时,其影长恰好为1块地砖长;当小军正好站在广场的点(距点9块地砖长)时,其影长恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高为1.6米,,,.请你根据以上信息求出小军身高的长.(精确到0.01)
14.在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
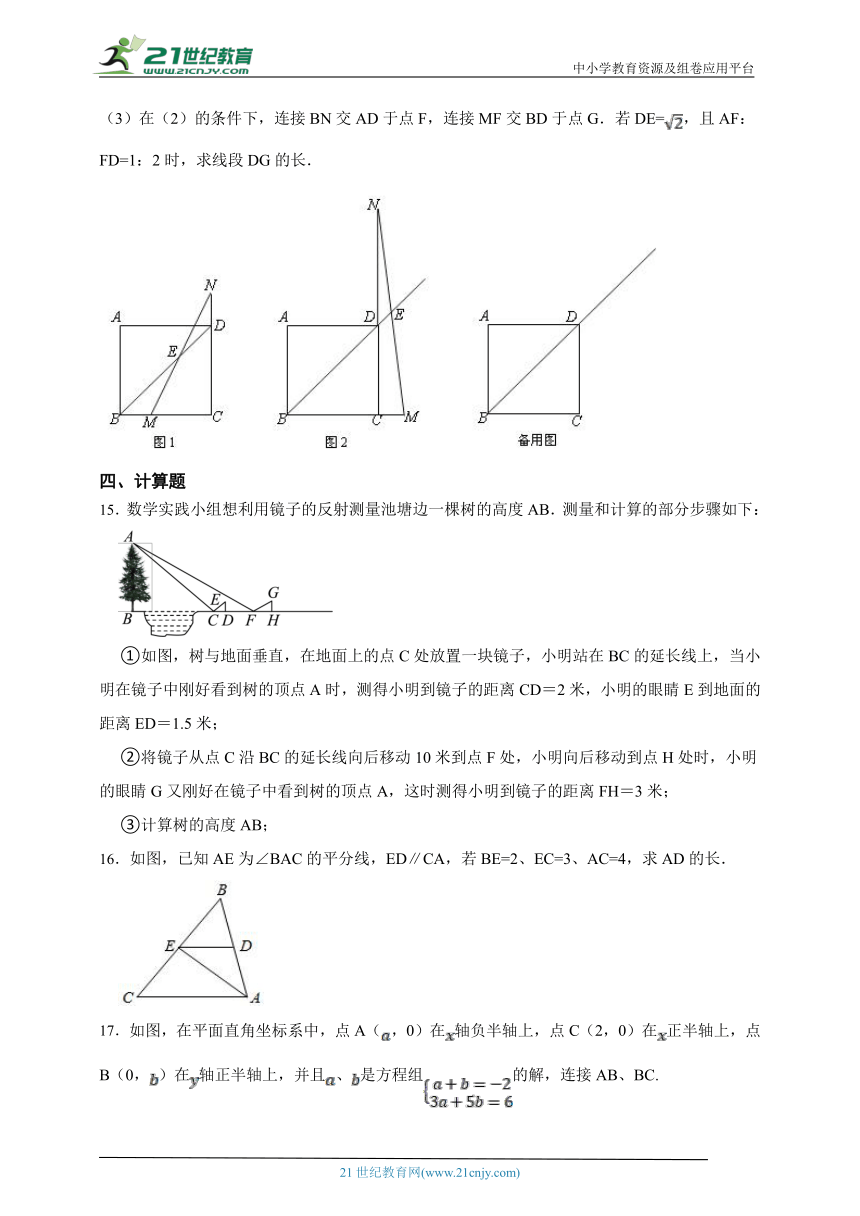
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=,且AF:FD=1:2时,求线段DG的长.
四、计算题
15.数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:
①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
16.如图,已知AE为∠BAC的平分线,ED∥CA,若BE=2、EC=3、AC=4,求AD的长.
17.如图,在平面直角坐标系中,点A(,0)在轴负半轴上,点C(2,0)在正半轴上,点B(0,)在轴正半轴上,并且、是方程组的解,连接AB、BC.
(1)=________,=________;
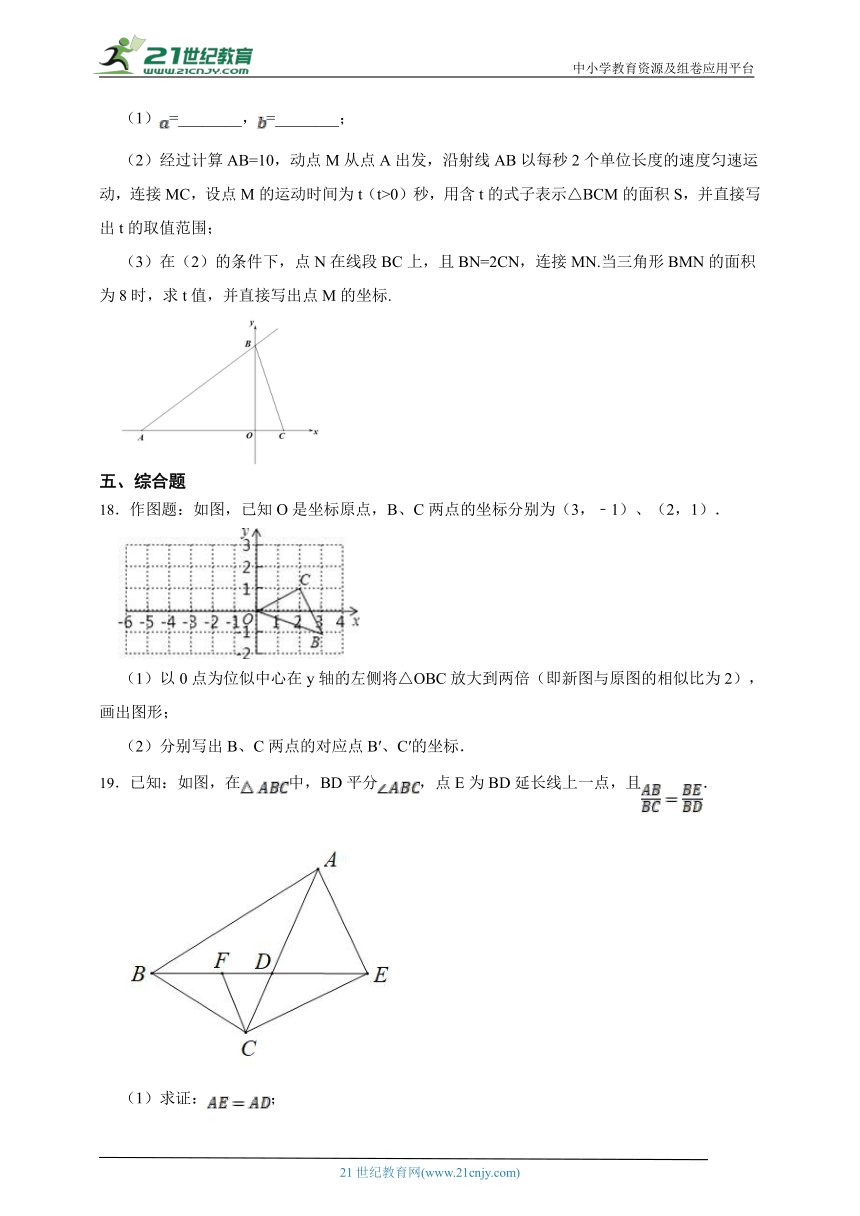
(2)经过计算AB=10,动点M从点A出发,沿射线AB以每秒2个单位长度的速度匀速运动,连接MC,设点M的运动时间为t(t>0)秒,用含t的式子表示△BCM的面积S,并直接写出t的取值范围;
(3)在(2)的条件下,点N在线段BC上,且BN=2CN,连接MN.当三角形BMN的面积为8时,求t值,并直接写出点M的坐标.
五、综合题
18.作图题:如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标.
19.已知:如图,在中,BD平分,点E为BD延长线上一点,且.
(1)求证:;
(2)若点F为线段BD上一点,,,,的面积为3,求的面积.
20.如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小
六、实践探究题
21.(探究)如图①,在 中,点D、E、F分别在边 、 、 上, , .
(1)求证: .
(2)若 、 的面积分别为 和 ,则 的值为 .
(3)(拓展)
如图②,在 中,点D、E分别在边 、 上,点F、G在边 上,且 , .若 、 、 的面积分别为3,7,5,则 的面积为 .
答案解析部分
1.【答案】2
【知识点】相似三角形的判定与性质
2.【答案】8
【知识点】相似三角形的判定与性质;三角形的中位线定理
3.【答案】16:25
【知识点】相似三角形的性质
4.【答案】64
【知识点】相似三角形的判定与性质
5.【答案】3
【知识点】相似三角形的应用
6.【答案】 或 .
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定与性质;等腰直角三角形
7.【答案】D
【知识点】图形的相似;相似三角形的性质
8.【答案】C
【知识点】平行线的判定;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
9.【答案】B
【知识点】相似三角形的性质
10.【答案】B
【知识点】相似三角形的性质
11.【答案】C
【知识点】相似三角形的性质;相似三角形的应用
12.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA
(2)解:设DC=x,
∵△ABD∽△CBA,
∴,
∴,
解得,x=9;
即CD=7
【知识点】相似三角形的判定与性质
13.【答案】解:,,,
,
米,米,米
又米,米
,.
米,米,米
米
答:小军的身高约为1.75米.
【知识点】相似三角形的应用
14.【答案】解:(1)过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
,
∴△EFM≌△EDN,
∴EF=ED,
∴BD-2DE=BF,
根据勾股定理得:BF=BM,
即BD-2DE=BM.
(2)过点M作MF⊥BC交BD于点F,与(1)证法类似:BD+2DE=BF=BM,
(3)由(2)知,BD+2DE=BM,BD=BC,
∵DE=,
∴CM=2,
∵AB∥CD,
∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
∴CD:ND=1:2,
CD:(CD+2)=1:2,
∴CD=2,∴FD=,
∴FD:BM=1:3,
∴DG:BG=1:3,
∴DG=.
【知识点】全等三角形的判定与性质;正方形的性质;相似三角形的判定与性质
15.【答案】树的高度AB为15米
【知识点】相似三角形的性质;相似三角形的判定
16.【答案】解:
,
,,
平分
等腰三角形
【知识点】相似三角形的判定与性质
17.【答案】(1)、;(2)①()②()(3)3或,或
【知识点】二元一次方程的解;坐标与图形性质;相似三角形的判定与性质
18.【答案】(1)解:△OB′C′是所求的三角形;
(2)解:B′的坐标是(﹣6,2),C′的坐标是(﹣4,﹣2).
【知识点】点的坐标;作图﹣相似变换
19.【答案】(1)证明:∵BD平分,
∴,
即.
又∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,,
又∵(BD是平分线),
∴,
∴,
∵,∴,
则,即,
∴,
∴.
∴.
即的面积是9.
【知识点】相似三角形的判定与性质
20.【答案】(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC= AO=OC=ED,CE=OD= OB=DQ,
在△PCE与△EDQ中,
,
∴△PCE≌△EDQ;
(2)解:如图2,连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
(3)解:如图3中,
由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,
∵△ARB∽△PEQ,
∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD= ∠ARB=45°,
∴∠MON=180°﹣∠CRD=135°.
【知识点】全等三角形的判定与性质;平行四边形的判定与性质;相似三角形的判定与性质
21.【答案】(1)证明:∵EF∥AB,DE∥BC,
∴四边形BFED是平行四边形,∠AED=∠C,
∴BF=DE,
∵EF∥AB,
∴ ,
∴ ,
∵∠AED=∠C,
∴△ADE∽△EFC(SAS).
(2)
(3)27
【知识点】相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】 22.3相似三角形的性质
一、填空题
1.如图,在 中, , ,垂足为 , ,则 的长为 .
2.如图,△ABC中,点D、E分别是AB、AC的中点,若S△ADE=2,则S△ABC= .
3.已知 ∽ ,AB: :5,那么 : .
4.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
5.两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20cm,光屏在距小孔30cm处,小华测量了蜡烛的火焰高度为2cm,则光屏上火焰所成像的高度为 cm.
6.在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE= a,连接AE,将△ABE沿AE折叠.若点B的对应点B′落在矩形ABCD的边上,则折痕的长为 .
二、单选题
7.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形对应边不成比例的一组是( )
A. B.
C. D.
8.在△ABC中,点D、E分别在边AB、AC上,如果AD=2,BD=4,那么由下列条件能够判断DE∥BC的是( )
A. = B. = C. = D. =
9. 若两个相似三角形的相似比为1:4,则它们的对应高的比为( )
A.1:2 B.1:4 C.1:8 D.1:16
10.如果两个相似三角形的相似比是1:2,那么它们的面积比是( )
A.1:2 B.1:4 C.1:3 D.2:1
11.已知:如图,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A. B. C. D.
三、解答题
12.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=6,BD=3,求CD的长.
13.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高,于是,两人在灯下沿直线移动,如图,当小聪正好站在广场的点(距点5块地砖长)时,其影长恰好为1块地砖长;当小军正好站在广场的点(距点9块地砖长)时,其影长恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高为1.6米,,,.请你根据以上信息求出小军身高的长.(精确到0.01)
14.在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=,且AF:FD=1:2时,求线段DG的长.
四、计算题
15.数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:
①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
16.如图,已知AE为∠BAC的平分线,ED∥CA,若BE=2、EC=3、AC=4,求AD的长.
17.如图,在平面直角坐标系中,点A(,0)在轴负半轴上,点C(2,0)在正半轴上,点B(0,)在轴正半轴上,并且、是方程组的解,连接AB、BC.
(1)=________,=________;
(2)经过计算AB=10,动点M从点A出发,沿射线AB以每秒2个单位长度的速度匀速运动,连接MC,设点M的运动时间为t(t>0)秒,用含t的式子表示△BCM的面积S,并直接写出t的取值范围;
(3)在(2)的条件下,点N在线段BC上,且BN=2CN,连接MN.当三角形BMN的面积为8时,求t值,并直接写出点M的坐标.
五、综合题
18.作图题:如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标.
19.已知:如图,在中,BD平分,点E为BD延长线上一点,且.
(1)求证:;
(2)若点F为线段BD上一点,,,,的面积为3,求的面积.
20.如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小
六、实践探究题
21.(探究)如图①,在 中,点D、E、F分别在边 、 、 上, , .
(1)求证: .
(2)若 、 的面积分别为 和 ,则 的值为 .
(3)(拓展)
如图②,在 中,点D、E分别在边 、 上,点F、G在边 上,且 , .若 、 、 的面积分别为3,7,5,则 的面积为 .
答案解析部分
1.【答案】2
【知识点】相似三角形的判定与性质
2.【答案】8
【知识点】相似三角形的判定与性质;三角形的中位线定理
3.【答案】16:25
【知识点】相似三角形的性质
4.【答案】64
【知识点】相似三角形的判定与性质
5.【答案】3
【知识点】相似三角形的应用
6.【答案】 或 .
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定与性质;等腰直角三角形
7.【答案】D
【知识点】图形的相似;相似三角形的性质
8.【答案】C
【知识点】平行线的判定;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
9.【答案】B
【知识点】相似三角形的性质
10.【答案】B
【知识点】相似三角形的性质
11.【答案】C
【知识点】相似三角形的性质;相似三角形的应用
12.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA
(2)解:设DC=x,
∵△ABD∽△CBA,
∴,
∴,
解得,x=9;
即CD=7
【知识点】相似三角形的判定与性质
13.【答案】解:,,,
,
米,米,米
又米,米
,.
米,米,米
米
答:小军的身高约为1.75米.
【知识点】相似三角形的应用
14.【答案】解:(1)过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
,
∴△EFM≌△EDN,
∴EF=ED,
∴BD-2DE=BF,
根据勾股定理得:BF=BM,
即BD-2DE=BM.
(2)过点M作MF⊥BC交BD于点F,与(1)证法类似:BD+2DE=BF=BM,
(3)由(2)知,BD+2DE=BM,BD=BC,
∵DE=,
∴CM=2,
∵AB∥CD,
∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
∴CD:ND=1:2,
CD:(CD+2)=1:2,
∴CD=2,∴FD=,
∴FD:BM=1:3,
∴DG:BG=1:3,
∴DG=.
【知识点】全等三角形的判定与性质;正方形的性质;相似三角形的判定与性质
15.【答案】树的高度AB为15米
【知识点】相似三角形的性质;相似三角形的判定
16.【答案】解:
,
,,
平分
等腰三角形
【知识点】相似三角形的判定与性质
17.【答案】(1)、;(2)①()②()(3)3或,或
【知识点】二元一次方程的解;坐标与图形性质;相似三角形的判定与性质
18.【答案】(1)解:△OB′C′是所求的三角形;
(2)解:B′的坐标是(﹣6,2),C′的坐标是(﹣4,﹣2).
【知识点】点的坐标;作图﹣相似变换
19.【答案】(1)证明:∵BD平分,
∴,
即.
又∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,,
又∵(BD是平分线),
∴,
∴,
∵,∴,
则,即,
∴,
∴.
∴.
即的面积是9.
【知识点】相似三角形的判定与性质
20.【答案】(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC= AO=OC=ED,CE=OD= OB=DQ,
在△PCE与△EDQ中,
,
∴△PCE≌△EDQ;
(2)解:如图2,连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
(3)解:如图3中,
由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,
∵△ARB∽△PEQ,
∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD= ∠ARB=45°,
∴∠MON=180°﹣∠CRD=135°.
【知识点】全等三角形的判定与性质;平行四边形的判定与性质;相似三角形的判定与性质
21.【答案】(1)证明:∵EF∥AB,DE∥BC,
∴四边形BFED是平行四边形,∠AED=∠C,
∴BF=DE,
∵EF∥AB,
∴ ,
∴ ,
∵∠AED=∠C,
∴△ADE∽△EFC(SAS).
(2)
(3)27
【知识点】相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
