【沪科版九上同步练习】 22.4 图形的位似变换(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 22.4 图形的位似变换(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
22.4图形的位似变换
一、单选题
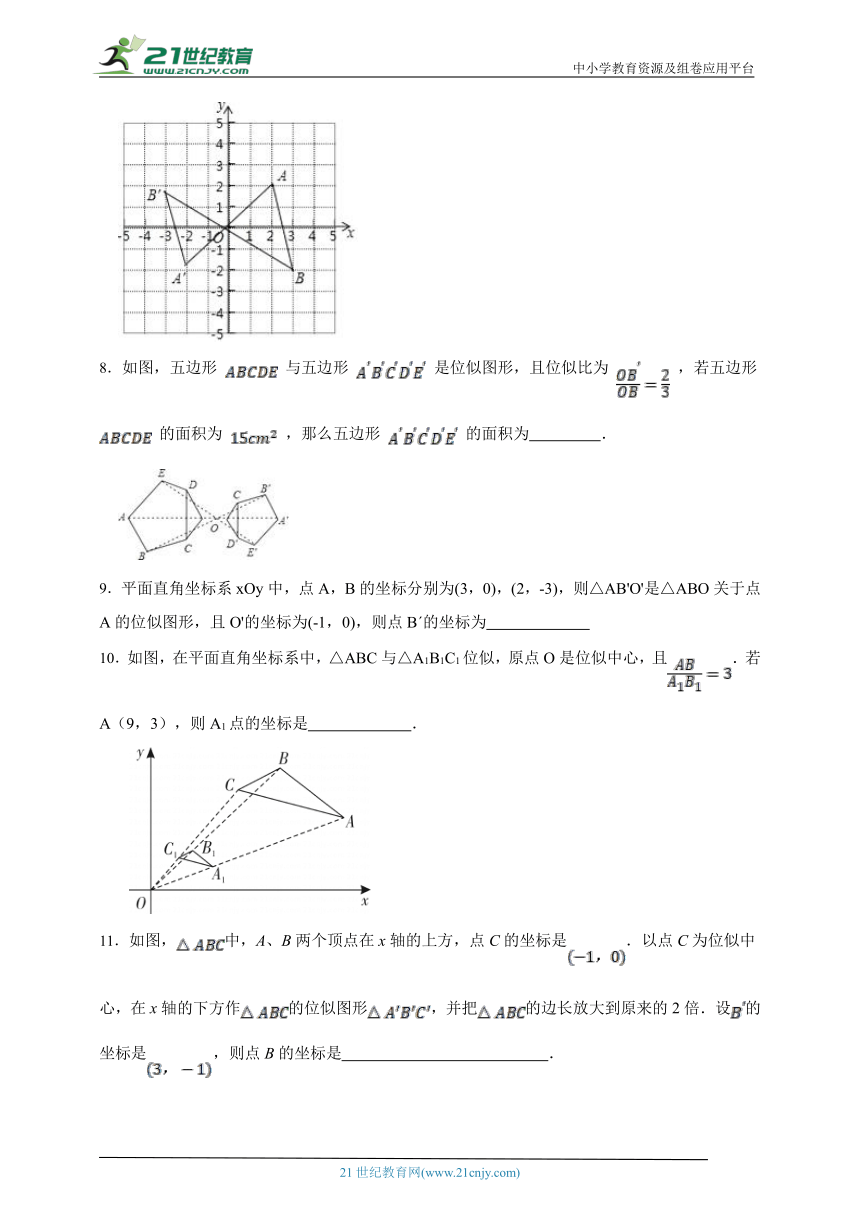
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点 的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
2.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
3.已知△ABC与△A'B'C'是位似图形,位似比是1:3,则△ABC与△A'B'C'的面积比是( )
A.1:3 B.1:6 C.1:9 D.3:1
4.如图,以点O为位似中心,把 放大为原图形的2倍得到 ,若 与 的位似比为k,则以下结论中正确的是( )
A. B. C. D.
5.下列说法正确的是( )
A.两个位似图形对应点连线有可能无交点
B.两个位似图形对应点连线交点个数为1或2
C.两个位似图形对应点连线只有一个交点
D.两个位似图形对应点连线交点个数不少于4个
二、填空题
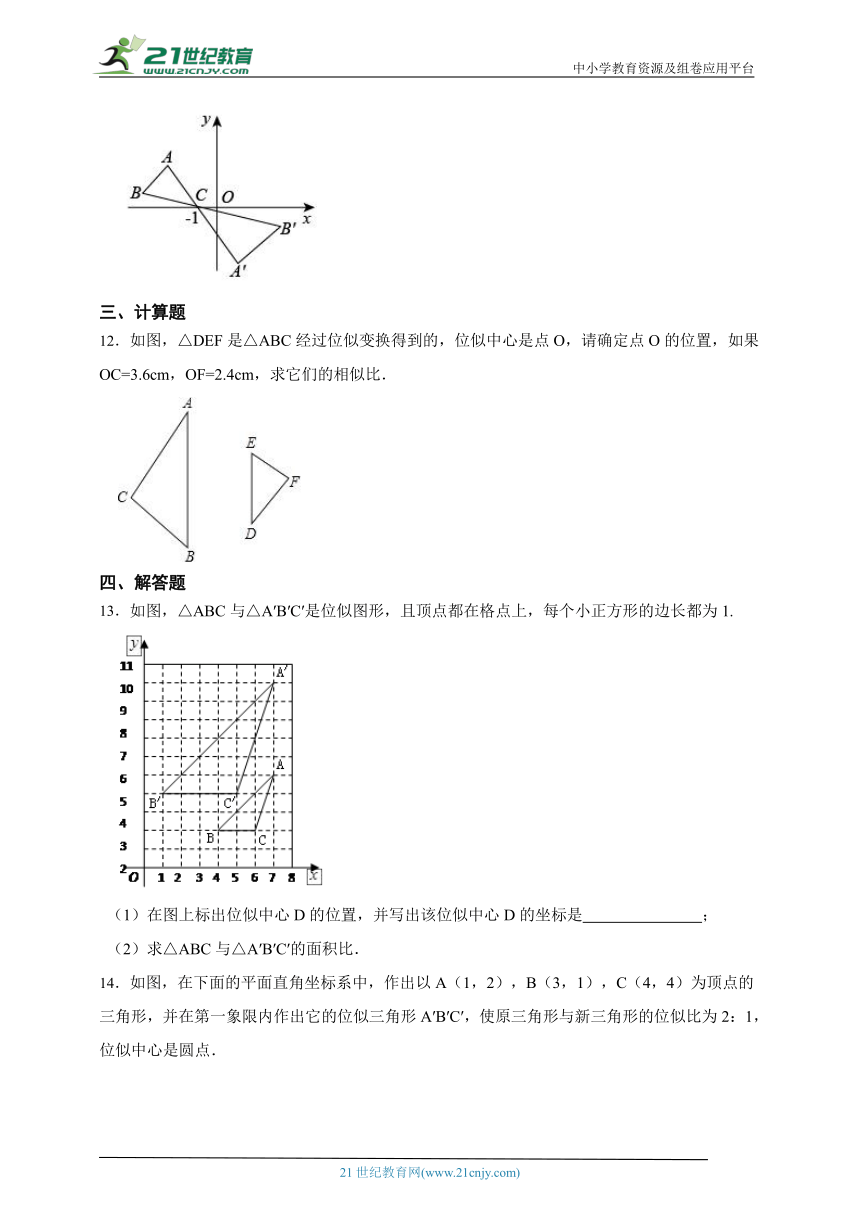
6.如图,已知顶点,以原点为位似中心,把缩小到原来的,则与点对应的点的坐标是 .
7.如图,在平面直角坐标系中,每个小方格的边长均为1.△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是 .
8.如图,五边形 与五边形 是位似图形,且位似比为 ,若五边形 的面积为 ,那么五边形 的面积为 .
9.平面直角坐标系xOy中,点A,B的坐标分别为(3,0),(2,-3),则△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(-1,0),则点B 的坐标为
10.如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且.若A(9,3),则A1点的坐标是 .
11.如图,中,A、B两个顶点在x轴的上方,点C的坐标是.以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍.设的坐标是,则点B的坐标是 .
三、计算题
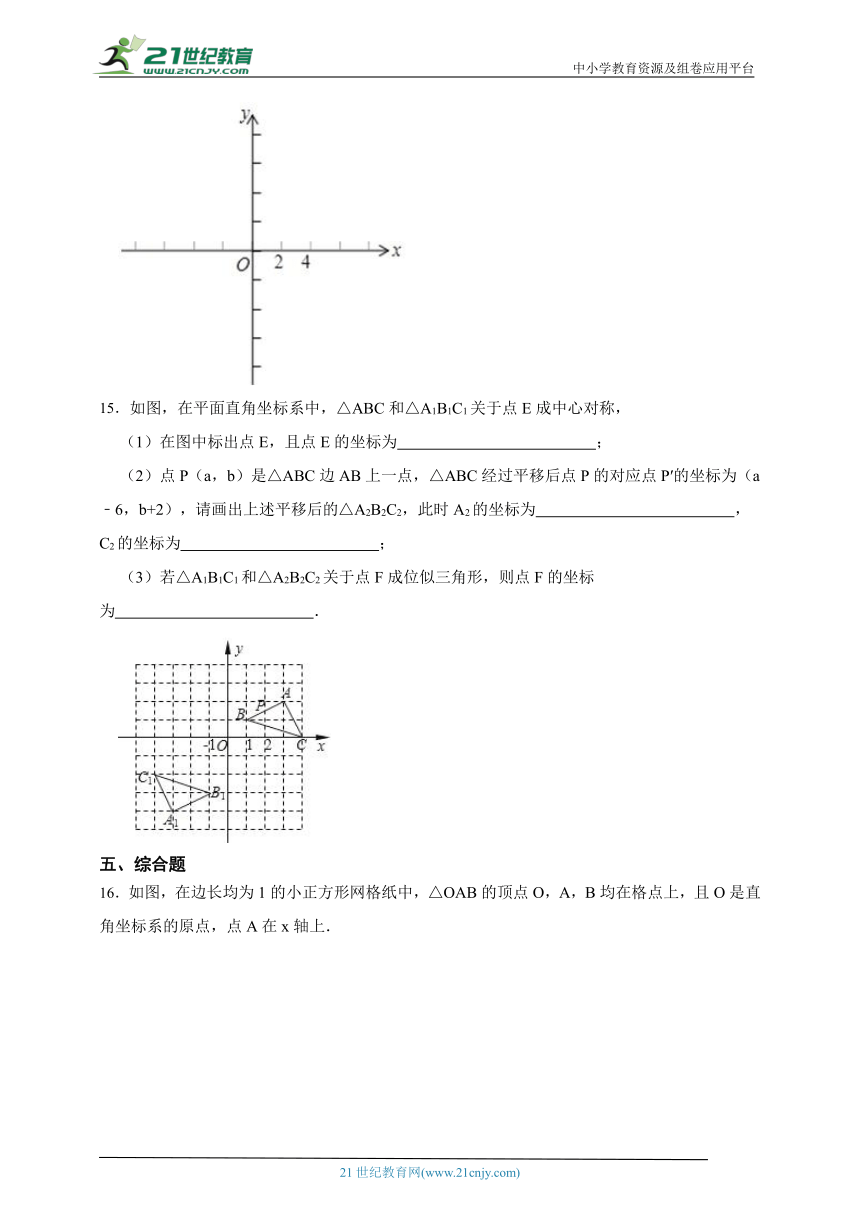
12.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
四、解答题
13.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
14.如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
15.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
五、综合题
16.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1,与△OAB对应线段的比为2:1,画出△OA1B1,(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标 ;
(3)直接写出tan∠OA1B1.
17.如图,点的坐标为,点的坐标为
①以点为旋转中心,将顺时针方向旋转90°,得到;
②以点为位似中心,将放大,使相似比为,且点在第三象限.
(1)在图中画出和;
(2)请直接写出点的坐标:( , )
(3)在上面的(2)问下,直接写出在线段上的任意动点的对应点的坐标:( , ).
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
答案解析部分
1.【答案】A
【知识点】位似变换
2.【答案】D
【知识点】轴对称的性质;平移的性质;位似变换;旋转的性质
3.【答案】C
【知识点】相似三角形的性质;位似变换
4.【答案】B
【知识点】位似变换
5.【答案】C
【知识点】位似变换
6.【答案】或
【知识点】位似变换;图形位似变换的点的坐标特征
7.【答案】(﹣2, )
【知识点】位似变换
8.【答案】
【知识点】位似变换
9.【答案】
【知识点】坐标与图形性质;相似三角形的判定与性质;位似变换
10.【答案】(3,1)
【知识点】位似变换
11.【答案】或
【知识点】位似变换;图形位似变换的点的坐标特征
12.【答案】解:连接AD,CF交于点O,
则点O即为所求;
∵OC=3.6cm,OF=2.4cm,
∴OC:OF=3:2,
∴△ABC与△DEF的相似比为3:2.
【知识点】位似变换
13.【答案】解:(1)如图:D(7,0);
(2)∵△ABC∽△A′B′C′
∴
【知识点】相似三角形的性质;作图﹣位似变换
14.【答案】解:如图,△ABC和△A′B′C′为所作.
【知识点】作图﹣位似变换
15.【答案】解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
【知识点】作图﹣平移;位似变换;中心对称及中心对称图形
16.【答案】(1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)
(3)解:2
【知识点】位似变换;锐角三角函数的定义
17.【答案】(1)解:如图,△AB1O1和△A2B2O2为所作;
(2)-3;-4
(3)3-2a;-2b
【知识点】作图﹣位似变换;作图﹣旋转
18.【答案】(1)解:如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2)
(2)解:如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4)
(3)解:如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
【知识点】作图﹣轴对称;作图﹣位似变换
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
22.4图形的位似变换
一、单选题
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点 的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
2.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
3.已知△ABC与△A'B'C'是位似图形,位似比是1:3,则△ABC与△A'B'C'的面积比是( )
A.1:3 B.1:6 C.1:9 D.3:1
4.如图,以点O为位似中心,把 放大为原图形的2倍得到 ,若 与 的位似比为k,则以下结论中正确的是( )
A. B. C. D.
5.下列说法正确的是( )
A.两个位似图形对应点连线有可能无交点
B.两个位似图形对应点连线交点个数为1或2
C.两个位似图形对应点连线只有一个交点
D.两个位似图形对应点连线交点个数不少于4个
二、填空题
6.如图,已知顶点,以原点为位似中心,把缩小到原来的,则与点对应的点的坐标是 .
7.如图,在平面直角坐标系中,每个小方格的边长均为1.△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是 .
8.如图,五边形 与五边形 是位似图形,且位似比为 ,若五边形 的面积为 ,那么五边形 的面积为 .
9.平面直角坐标系xOy中,点A,B的坐标分别为(3,0),(2,-3),则△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(-1,0),则点B 的坐标为
10.如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且.若A(9,3),则A1点的坐标是 .
11.如图,中,A、B两个顶点在x轴的上方,点C的坐标是.以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍.设的坐标是,则点B的坐标是 .
三、计算题
12.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
四、解答题
13.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
14.如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
15.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
五、综合题
16.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1,与△OAB对应线段的比为2:1,画出△OA1B1,(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标 ;
(3)直接写出tan∠OA1B1.
17.如图,点的坐标为,点的坐标为
①以点为旋转中心,将顺时针方向旋转90°,得到;
②以点为位似中心,将放大,使相似比为,且点在第三象限.
(1)在图中画出和;
(2)请直接写出点的坐标:( , )
(3)在上面的(2)问下,直接写出在线段上的任意动点的对应点的坐标:( , ).
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
答案解析部分
1.【答案】A
【知识点】位似变换
2.【答案】D
【知识点】轴对称的性质;平移的性质;位似变换;旋转的性质
3.【答案】C
【知识点】相似三角形的性质;位似变换
4.【答案】B
【知识点】位似变换
5.【答案】C
【知识点】位似变换
6.【答案】或
【知识点】位似变换;图形位似变换的点的坐标特征
7.【答案】(﹣2, )
【知识点】位似变换
8.【答案】
【知识点】位似变换
9.【答案】
【知识点】坐标与图形性质;相似三角形的判定与性质;位似变换
10.【答案】(3,1)
【知识点】位似变换
11.【答案】或
【知识点】位似变换;图形位似变换的点的坐标特征
12.【答案】解:连接AD,CF交于点O,
则点O即为所求;
∵OC=3.6cm,OF=2.4cm,
∴OC:OF=3:2,
∴△ABC与△DEF的相似比为3:2.
【知识点】位似变换
13.【答案】解:(1)如图:D(7,0);
(2)∵△ABC∽△A′B′C′
∴
【知识点】相似三角形的性质;作图﹣位似变换
14.【答案】解:如图,△ABC和△A′B′C′为所作.
【知识点】作图﹣位似变换
15.【答案】解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
【知识点】作图﹣平移;位似变换;中心对称及中心对称图形
16.【答案】(1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)
(3)解:2
【知识点】位似变换;锐角三角函数的定义
17.【答案】(1)解:如图,△AB1O1和△A2B2O2为所作;
(2)-3;-4
(3)3-2a;-2b
【知识点】作图﹣位似变换;作图﹣旋转
18.【答案】(1)解:如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2)
(2)解:如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4)
(3)解:如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
【知识点】作图﹣轴对称;作图﹣位似变换
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
