【沪科版九上同步练习】 第22章 相似形(基础知识)检测题(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 第22章 相似形(基础知识)检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 19:48:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
第22章相似形(基础知识)检测题
一、单选题
1.如图,平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )
A. B.
C. D.
2.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )
A. B. C. D.
3.下列各组的四条线段是成比例线段的是( )
A. B.
C. D.
4.若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )
A.2 B.3 C.4 D.5
5.如图,DE是ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4: 3
二、填空题
6.如图,在△ABC中,D、E、F分别为边AB、AC、BC上的点,连接DE、EF。若DE∥BC,EF∥AB,则图中共有 对相似三角形.
7.如果将一个三角形保持形状不变但周长扩大为原三角形周长的9倍,那么扩大后的三角形面积为原三角形面积的 倍.
8.如图,在平行四边形中,是边上的中点,连接,并延长交延长线于点,则与平行四边形的面积之比是 .
9.如图,在中,,,分别是,上的点,将沿着折叠,使点落在边的中点(记为处.若,,则的长为 .
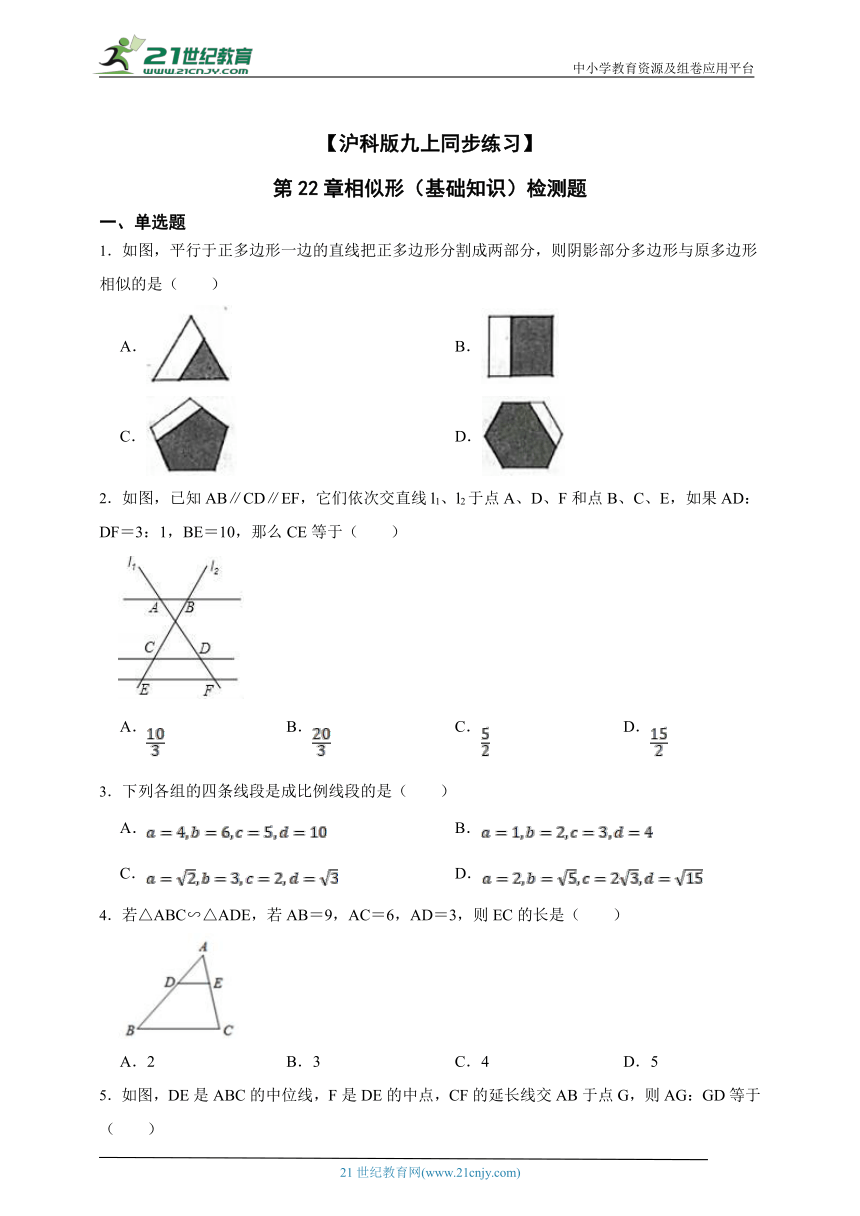
10.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为 米.
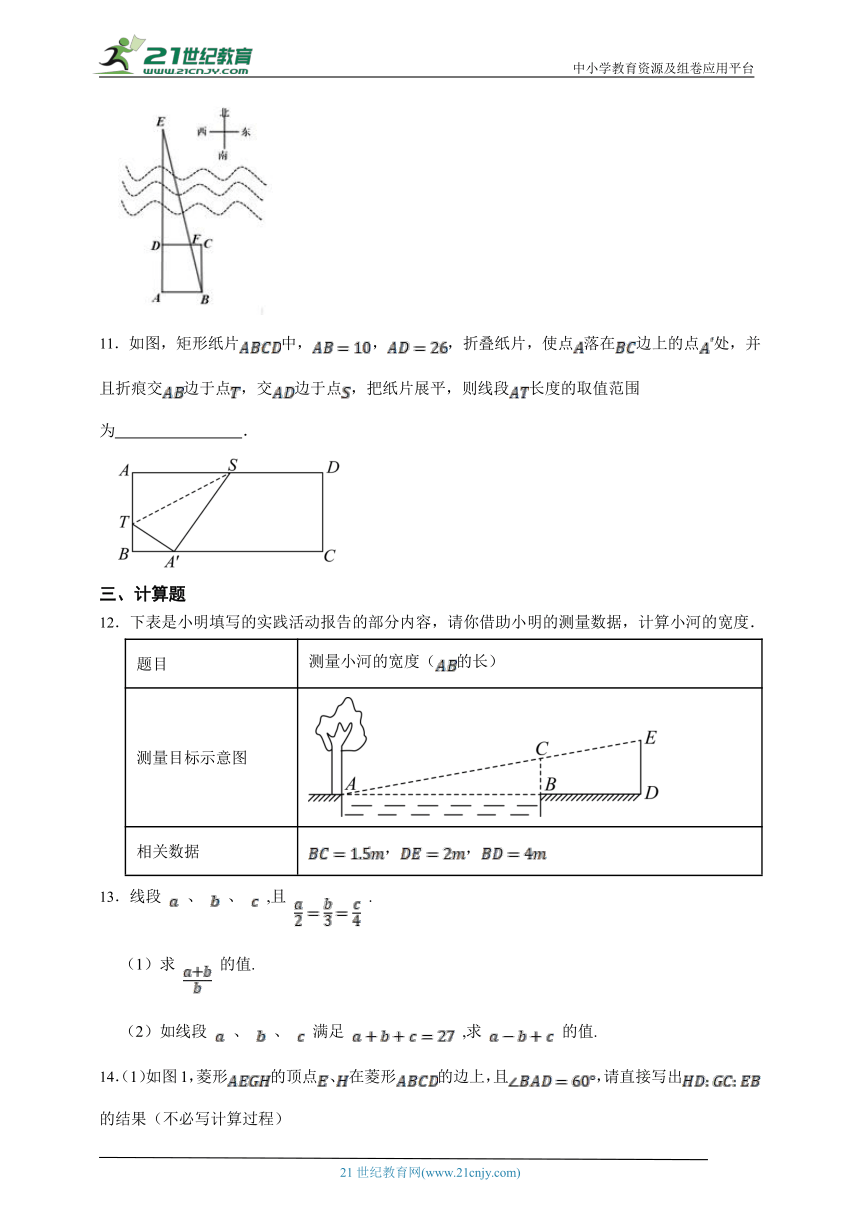
11.如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为 .
三、计算题
12.下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度(的长)
测量目标示意图
相关数据 ,,
13.线段 、 、 ,且 .
(1)求 的值.
(2)如线段 、 、 满足 ,求 的值.
14.(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
15.一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
16.如图,△ABC的高AD、BE交于点F,求证: = .
17.如图1,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在左侧),与y轴交于点C,点P为直线BC上方抛物线上的一个动点,过点P作PD‖y轴交BC于点D.
(1)求点A、B、C的坐标;
(2)设点P的横坐标为m,请用含m的式子表示线段PD的长;
(3)如图2,连接OP,交线段BC于点Q,连接PC,若△PCQ的面积为S1,△OCQ的面积为S2,则是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
五、综合题
18.
(1)已知线段,,求线段a,b的比例中项线段c的长度.
(2)已知,求的值.
19.已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA BD=BC BE
(1)求证:DE AB=AC BE;
(2)如果AC2=AD AB,求证:AE=AC.
20.如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
六、实践探究题
21.视力表中蕴含着很多数学知识,如:每个“”形图都是正方形结构,同一行的“”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值,测得对应行的“”形图边长,在平面直角坐标系中描点如图1.探究1检测距离为5米时,归纳与的关系式,并求视力值1.2所对应行的“”形图边长.
素材2图2为视网膜成像示意图,在检测视力时,眼晴能看清最小“”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).探究2当时,属于正常视力,根据函数增减性写出对应的分辦视角的范围.
素材3如图3,当确定时,在处用边长为的号“”测得的视力与在处用边长为的Ⅱ号“”测得的视力相同.探究3若检测距离为3米,求视力值1.2所对应行的“”形图边长.
答案解析部分
1.【答案】A
【知识点】相似多边形
2.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】D
【知识点】比例线段
4.【答案】C
【知识点】相似三角形的性质
5.【答案】A
【知识点】相似三角形的判定与性质;三角形的中位线定理
6.【答案】3
【知识点】相似三角形的判定
7.【答案】81
【知识点】相似三角形的性质
8.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
9.【答案】
【知识点】勾股定理;翻折变换(折叠问题);相似三角形的判定与性质;直角三角形斜边上的中线
10.【答案】25
【知识点】相似三角形的应用
11.【答案】
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
12.【答案】12米
【知识点】相似三角形的应用
13.【答案】(1)解: ,
;
(2)解:设 =k, 则a=2k, b=3k, c=4k,
由a+b+c=27,由2k+3k+4k=27,得:k=3,
a=6,b=9,c=12
故 =6-9+12=9,
【知识点】比例的性质
14.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】解答:设另一个三角形的两边长是xcm,ycm,由题意,得:x:5=y:8=4.8:12,解得x=2cm,y=3.2cm.因此另两条边的边长为2cm,3.2cm.
【知识点】相似三角形的性质
16.【答案】证明:∵△ABC的高A
D、BE交于点F,
∴∠EBC+∠C=∠DAC+∠C=90°,
∴∠EBC=∠DAC,即∠FBD=∠FAE,
而∠AEF=∠BDF,
∴△AEF∽△BDF,
∴ .
【知识点】余角、补角及其性质;相似三角形的判定与性质
17.【答案】(1)解:∵当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3.
∴A(-1,0),B(3,0).
∵当x=0时,y=3,
∴C(0,3).
(2)解:∵B(3、0),C(0、3),设直线BC的函数解析式为y=kx+3,
∴0=3k+3.解得k=-1.
∴直线BC的函数解析式为y=-x+3.
设点Р的横坐标为m、则P(m,-m2+2m+3),
∵PD∥y轴交直线BC于点D,
∴D(m,-m+3)
∴PD=-m2+2m+3-(-m+3)=-m2+3m;
(3)解:有最大值,最大值为.理由如下:
如图2,
过点C作CQ⊥OP交OP于点H,
,,
∴.
∵PD∥y轴,
∴∠DPQ=∠COQ,∠PDQ=∠OCQ,
∴△DPQ~△COQ.
∴.
∵,
∴当m=时,取得最大值.
【知识点】相似三角形的性质;相似三角形的判定;二次函数与一次函数的综合应用;二次函数-动态几何问题
18.【答案】(1)解:∵线段c是线段a、b的比例中项,
∴c2=ab,
又∵a=4,b=9,
∴c2=4×9=36,
∴c=6(负值已舍),
∴ 线段a,b的比例中项线段c的长度的是6.
(2)解:设,,
∴.
【知识点】比例的性质;比例线段
19.【答案】(1)证明:∵BA BD=BC BE,
∴ ,
又∵∠B=∠B,
∴△ABC∽△EBD,
∴ ,
∴DE AB=AC BE;
(2)证明:∵AC2=AD AB,
∴ ,
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴∠ACD=∠B,
∵ ,∠B=∠B,
∴△BAE∽△BCD,
∴∠BAE=∠BCD,
∵∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD,
∴∠AEC=∠ACE,
∴AE=AC.
【知识点】相似三角形的判定与性质
20.【答案】(1)解∵四边形ABDF是矩形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)解:过点Q作QE⊥DP,垂足为E,则DE= DP,如图所示:
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴ = ,
∴AP·DQ=DP·DE= DP2.
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP·DQ= (36+AP2).
∵点P在AB上,
∴AP≤4,
∴AP·DQ≤26,即AP·DQ的最大值为26.
(3)解∵P为AB的中点,
∴AP=BP= AB=2,
由(2)得,DQ= (36+22)=10.
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴ = ,
即 = ,解得x= ,
∴BG=6- = ,
∴PG=.
【知识点】等腰三角形的判定;勾股定理;矩形的性质;相似三角形的判定与性质
21.【答案】解:探究1由图象中的点的坐标规律得到n与b成反比例关系.
设,
将其中一点代人得,解得
将其余各点一 一代人验证,均相当精确地符合关系式.
将代人得;
答:检测距离为5米时,视力值1.2所对应行的“”形图边长为,
探究2∵,
∴在自变量的取值范围内,n随着的增大而减小,
当时,.
.
探究3由素材可知,当某人的视力确定时,其分辨视角也是确定的,
∴由相似三角形性质可得:
由探究1知可得,
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为mm.
【知识点】反比例函数的实际应用;相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
第22章相似形(基础知识)检测题
一、单选题
1.如图,平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )
A. B.
C. D.
2.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )
A. B. C. D.
3.下列各组的四条线段是成比例线段的是( )
A. B.
C. D.
4.若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )
A.2 B.3 C.4 D.5
5.如图,DE是ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4: 3
二、填空题
6.如图,在△ABC中,D、E、F分别为边AB、AC、BC上的点,连接DE、EF。若DE∥BC,EF∥AB,则图中共有 对相似三角形.
7.如果将一个三角形保持形状不变但周长扩大为原三角形周长的9倍,那么扩大后的三角形面积为原三角形面积的 倍.
8.如图,在平行四边形中,是边上的中点,连接,并延长交延长线于点,则与平行四边形的面积之比是 .
9.如图,在中,,,分别是,上的点,将沿着折叠,使点落在边的中点(记为处.若,,则的长为 .
10.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为 米.
11.如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为 .
三、计算题
12.下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度(的长)
测量目标示意图
相关数据 ,,
13.线段 、 、 ,且 .
(1)求 的值.
(2)如线段 、 、 满足 ,求 的值.
14.(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
15.一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
16.如图,△ABC的高AD、BE交于点F,求证: = .
17.如图1,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在左侧),与y轴交于点C,点P为直线BC上方抛物线上的一个动点,过点P作PD‖y轴交BC于点D.
(1)求点A、B、C的坐标;
(2)设点P的横坐标为m,请用含m的式子表示线段PD的长;
(3)如图2,连接OP,交线段BC于点Q,连接PC,若△PCQ的面积为S1,△OCQ的面积为S2,则是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
五、综合题
18.
(1)已知线段,,求线段a,b的比例中项线段c的长度.
(2)已知,求的值.
19.已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA BD=BC BE
(1)求证:DE AB=AC BE;
(2)如果AC2=AD AB,求证:AE=AC.
20.如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
六、实践探究题
21.视力表中蕴含着很多数学知识,如:每个“”形图都是正方形结构,同一行的“”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值,测得对应行的“”形图边长,在平面直角坐标系中描点如图1.探究1检测距离为5米时,归纳与的关系式,并求视力值1.2所对应行的“”形图边长.
素材2图2为视网膜成像示意图,在检测视力时,眼晴能看清最小“”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).探究2当时,属于正常视力,根据函数增减性写出对应的分辦视角的范围.
素材3如图3,当确定时,在处用边长为的号“”测得的视力与在处用边长为的Ⅱ号“”测得的视力相同.探究3若检测距离为3米,求视力值1.2所对应行的“”形图边长.
答案解析部分
1.【答案】A
【知识点】相似多边形
2.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】D
【知识点】比例线段
4.【答案】C
【知识点】相似三角形的性质
5.【答案】A
【知识点】相似三角形的判定与性质;三角形的中位线定理
6.【答案】3
【知识点】相似三角形的判定
7.【答案】81
【知识点】相似三角形的性质
8.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
9.【答案】
【知识点】勾股定理;翻折变换(折叠问题);相似三角形的判定与性质;直角三角形斜边上的中线
10.【答案】25
【知识点】相似三角形的应用
11.【答案】
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
12.【答案】12米
【知识点】相似三角形的应用
13.【答案】(1)解: ,
;
(2)解:设 =k, 则a=2k, b=3k, c=4k,
由a+b+c=27,由2k+3k+4k=27,得:k=3,
a=6,b=9,c=12
故 =6-9+12=9,
【知识点】比例的性质
14.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】解答:设另一个三角形的两边长是xcm,ycm,由题意,得:x:5=y:8=4.8:12,解得x=2cm,y=3.2cm.因此另两条边的边长为2cm,3.2cm.
【知识点】相似三角形的性质
16.【答案】证明:∵△ABC的高A
D、BE交于点F,
∴∠EBC+∠C=∠DAC+∠C=90°,
∴∠EBC=∠DAC,即∠FBD=∠FAE,
而∠AEF=∠BDF,
∴△AEF∽△BDF,
∴ .
【知识点】余角、补角及其性质;相似三角形的判定与性质
17.【答案】(1)解:∵当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3.
∴A(-1,0),B(3,0).
∵当x=0时,y=3,
∴C(0,3).
(2)解:∵B(3、0),C(0、3),设直线BC的函数解析式为y=kx+3,
∴0=3k+3.解得k=-1.
∴直线BC的函数解析式为y=-x+3.
设点Р的横坐标为m、则P(m,-m2+2m+3),
∵PD∥y轴交直线BC于点D,
∴D(m,-m+3)
∴PD=-m2+2m+3-(-m+3)=-m2+3m;
(3)解:有最大值,最大值为.理由如下:
如图2,
过点C作CQ⊥OP交OP于点H,
,,
∴.
∵PD∥y轴,
∴∠DPQ=∠COQ,∠PDQ=∠OCQ,
∴△DPQ~△COQ.
∴.
∵,
∴当m=时,取得最大值.
【知识点】相似三角形的性质;相似三角形的判定;二次函数与一次函数的综合应用;二次函数-动态几何问题
18.【答案】(1)解:∵线段c是线段a、b的比例中项,
∴c2=ab,
又∵a=4,b=9,
∴c2=4×9=36,
∴c=6(负值已舍),
∴ 线段a,b的比例中项线段c的长度的是6.
(2)解:设,,
∴.
【知识点】比例的性质;比例线段
19.【答案】(1)证明:∵BA BD=BC BE,
∴ ,
又∵∠B=∠B,
∴△ABC∽△EBD,
∴ ,
∴DE AB=AC BE;
(2)证明:∵AC2=AD AB,
∴ ,
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴∠ACD=∠B,
∵ ,∠B=∠B,
∴△BAE∽△BCD,
∴∠BAE=∠BCD,
∵∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD,
∴∠AEC=∠ACE,
∴AE=AC.
【知识点】相似三角形的判定与性质
20.【答案】(1)解∵四边形ABDF是矩形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)解:过点Q作QE⊥DP,垂足为E,则DE= DP,如图所示:
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴ = ,
∴AP·DQ=DP·DE= DP2.
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP·DQ= (36+AP2).
∵点P在AB上,
∴AP≤4,
∴AP·DQ≤26,即AP·DQ的最大值为26.
(3)解∵P为AB的中点,
∴AP=BP= AB=2,
由(2)得,DQ= (36+22)=10.
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴ = ,
即 = ,解得x= ,
∴BG=6- = ,
∴PG=.
【知识点】等腰三角形的判定;勾股定理;矩形的性质;相似三角形的判定与性质
21.【答案】解:探究1由图象中的点的坐标规律得到n与b成反比例关系.
设,
将其中一点代人得,解得
将其余各点一 一代人验证,均相当精确地符合关系式.
将代人得;
答:检测距离为5米时,视力值1.2所对应行的“”形图边长为,
探究2∵,
∴在自变量的取值范围内,n随着的增大而减小,
当时,.
.
探究3由素材可知,当某人的视力确定时,其分辨视角也是确定的,
∴由相似三角形性质可得:
由探究1知可得,
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为mm.
【知识点】反比例函数的实际应用;相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
