【沪科版九上同步练习】 第22章 相似形(能力培养)检测题(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】 第22章 相似形(能力培养)检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
第22章相似形(能力培养)检测题
一、单选题
1.若两个相似多边形的相似比为,则它们周长的比为( )
A. B. C. D.
2.如图,,,,则的长是( )
A.3 B.4 C.6 D.10
3.已知线段,,是线段,的比例中项,则线段的长为( )
A.或 B. C. D.
4.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
5.如图,在中,点、分别为、的中点,连接,则( )
A. B. C.2 D.4
二、填空题
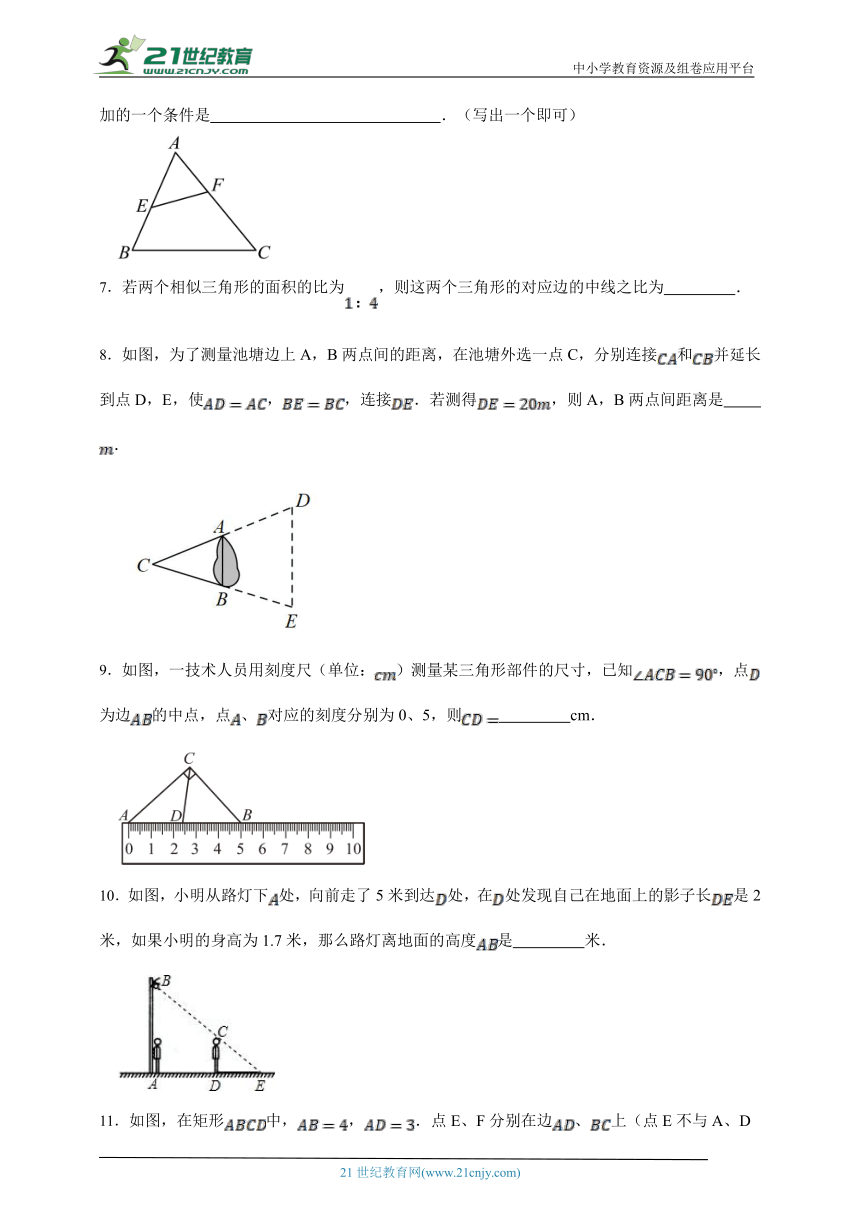
6.已知:如图,在中,点在边上,点在边上,要使,则需要增加的一个条件是 .(写出一个即可)
7.若两个相似三角形的面积的比为,则这两个三角形的对应边的中线之比为 .
8.如图,为了测量池塘边上A,B两点间的距离,在池塘外选一点C,分别连接和并延长到点D,E,使,,连接.若测得,则A,B两点间距离是 .
9.如图,一技术人员用刻度尺(单位:)测量某三角形部件的尺寸,已知,点为边的中点,点、对应的刻度分别为0、5,则 cm.
10.如图,小明从路灯下处,向前走了5米到达处,在处发现自己在地面上的影子长是2米,如果小明的身高为1.7米,那么路灯离地面的高度是 米.
11.如图,在矩形中,,.点E、F分别在边、上(点E不与A、D重合)且,于点P,交于点Q,于点M,交于点N.给出下面四个结论:
①四边形是矩形;
②平分四边形的周长;
③;
④当时,四边形的面积为2.
上述结论中,所有正确结论的序号是 .
三、计算题
12.已知 .
(1)求 的值.
(2)求 的值.
13.下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度(的长)
测量目标示意图
相关数据 ,,
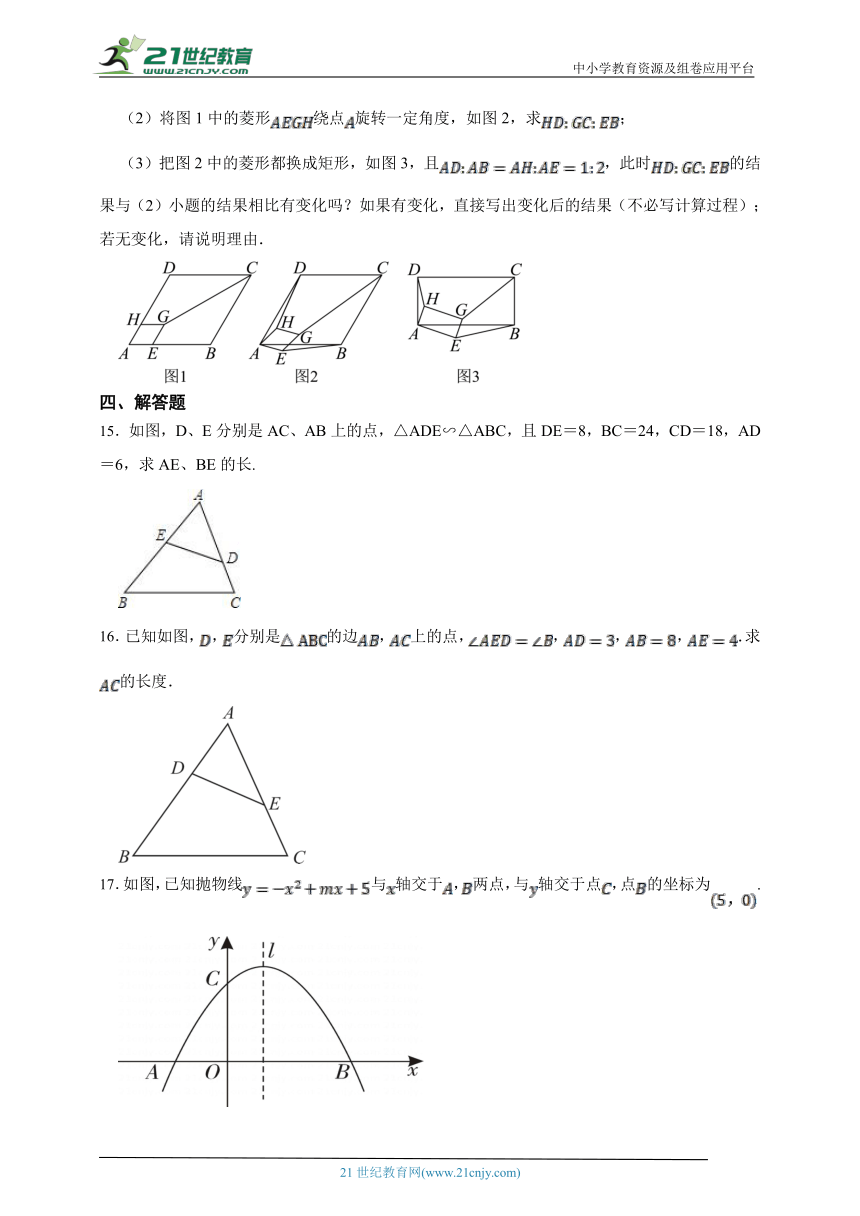
14.(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
15.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长.
16.已知如图,,分别是的边,上的点,,,,.求的长度.
17.如图,已知抛物线与轴交于,两点,与轴交于点,点的坐标为.
(1)求的值及抛物线的顶点坐标.
(2)点是抛物线对称轴上的一个动点,当的值最小时,求点的坐标.
五、综合题
18.(1)已知线段a=2,b=9,求线段a,b的比例中项.
(2)已知x:y=4:3,求的值.
19.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
20.在△ABC中,D为边AC上一点.
(1)如图1,若,求证:;
(2)如图2,F为线段BD上一点,且满足
①当,,点F为BD中点时,求CD的长;
②延长CF交AB于E,当点D为AC中点且时,直接写出的值为 ▲ .
六、实践探究题
21.某校项目式学习小组开展项目活动,过程如下:
项目主题:测量旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
方案一 方案二 …
测量工具 标杆,皮尺 自制直角三角板硬纸板,皮尺 …
测量示意图 说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上. 说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上.
测量数据 B,D之间的距离 16.8m B,D之间的距离 16.8m …
D,F之间的距离 1.35m EF的长度 0.50m …
EF的长度 2.60m CE的长度 0.75m …
… …
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
答案解析部分
1.【答案】B
【知识点】相似多边形
2.【答案】A
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】B
【知识点】比例线段
4.【答案】A
【知识点】相似三角形的性质
5.【答案】A
【知识点】三角形的中位线定理
6.【答案】(答案不唯一)
【知识点】相似三角形的判定
7.【答案】1∶2
【知识点】相似三角形的性质
8.【答案】
【知识点】相似三角形的判定与性质
9.【答案】
【知识点】直角三角形斜边上的中线
10.【答案】5.95
【知识点】相似三角形的应用
11.【答案】①②④
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
12.【答案】(1)解:∵ ,
∴设 ,
则 ,
∴ ;
(2)解:
【知识点】比例的性质
13.【答案】12米
【知识点】相似三角形的应用
14.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】解:∵△ADE∽△ABC,
∴,
∵DE=8,BC=24,CD=18,AD=6,
∴AC=AD+CD=24,
∴AE=8,AB=18,
∴BE=AB-AE=10.
【知识点】相似三角形的性质
16.【答案】
【知识点】相似三角形的判定与性质
17.【答案】(1)解:将点代入得,,,
∴抛物线解析式为
,
∴抛物线的顶点坐标为;
(2)解:如下图,点与点是关于直线成轴对称,根据其性质有,,
当点、点、点共线时,为最小值,即为的最小值,
由抛物线解析式为,可得点坐标为,点坐标为,对称轴为,
设直线的解释为,
将点,点,代入得,,解得,
∴直线的解析式为,联立方程,
,解得
∴当的值最小时,点的坐标为.
【知识点】二次函数-动态几何问题
18.【答案】(1)解:设线段x是线段a,b的比例中项,
∵a=3,b=6,
x2=3×6=18,
x=(负值舍去).
∴线段a,b的比例中项是3.
(2)解:设x=4k,y=3k,
∴==.
【知识点】比例的性质;比例线段
19.【答案】(1)解:如图1中,∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD= ∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线
(2)解:①当AD=CD时,如图2,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
②当AD=AC时,如图3中,∠ACD=∠ADC= =66°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°.
③当AC=CD时,如图4中,∠ADC=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍弃.
∴∠ACB=96°或114°.
(3)解:由已知AC=AD=2,
∵△BCD∽△BAC,
∴ ,设BD=x,
∴( )2=x(x+2),
∵x>0,
∴x= ﹣1,
∵△BCD∽△BAC,
∴ = = ,
∴CD= ×2= ﹣
【知识点】相似三角形的判定与性质
20.【答案】(1)证明:∵,∠A=∠A,
∴△ABD∽△ACB,
∴,
∴
(2)解:①过点F作FM∥AB,交AC于M,
∴∠MFD=∠ABD,
∵,
∴∠MFD=∠MCF,
∵∠FMD=∠CMF,
∴△FMD∽△CMF,
∴,
∵FM∥AB,点F为BD中点,
∴FM是△ABD的中位线,
∴,AM=MD,
设AM=MD=x,
∴,
解得或(舍去),
∴CD=AC-AD=;
②
【知识点】相似三角形的判定与性质
21.【答案】解:方案一:过C作CH∥BD交EF于Q,交AB于H,
则四边形CDFQ,四边形CDBH都是矩形,
∴CQ=DF=1.35m,CH=BD=16.8m,
∵EQ∥AH,
∴
∵
∴△CEQ∽△CAH,
∴,
即:,
解得:AB=12.9m;
方案二:(1)∵∠ACG=∠ACG,∠CGA=∠AEF=90°.
∴△CEF∽△CGA,
∴,
即:,
解得:AB=12.9m;
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
第22章相似形(能力培养)检测题
一、单选题
1.若两个相似多边形的相似比为,则它们周长的比为( )
A. B. C. D.
2.如图,,,,则的长是( )
A.3 B.4 C.6 D.10
3.已知线段,,是线段,的比例中项,则线段的长为( )
A.或 B. C. D.
4.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
5.如图,在中,点、分别为、的中点,连接,则( )
A. B. C.2 D.4
二、填空题
6.已知:如图,在中,点在边上,点在边上,要使,则需要增加的一个条件是 .(写出一个即可)
7.若两个相似三角形的面积的比为,则这两个三角形的对应边的中线之比为 .
8.如图,为了测量池塘边上A,B两点间的距离,在池塘外选一点C,分别连接和并延长到点D,E,使,,连接.若测得,则A,B两点间距离是 .
9.如图,一技术人员用刻度尺(单位:)测量某三角形部件的尺寸,已知,点为边的中点,点、对应的刻度分别为0、5,则 cm.
10.如图,小明从路灯下处,向前走了5米到达处,在处发现自己在地面上的影子长是2米,如果小明的身高为1.7米,那么路灯离地面的高度是 米.
11.如图,在矩形中,,.点E、F分别在边、上(点E不与A、D重合)且,于点P,交于点Q,于点M,交于点N.给出下面四个结论:
①四边形是矩形;
②平分四边形的周长;
③;
④当时,四边形的面积为2.
上述结论中,所有正确结论的序号是 .
三、计算题
12.已知 .
(1)求 的值.
(2)求 的值.
13.下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
题目 测量小河的宽度(的长)
测量目标示意图
相关数据 ,,
14.(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
15.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长.
16.已知如图,,分别是的边,上的点,,,,.求的长度.
17.如图,已知抛物线与轴交于,两点,与轴交于点,点的坐标为.
(1)求的值及抛物线的顶点坐标.
(2)点是抛物线对称轴上的一个动点,当的值最小时,求点的坐标.
五、综合题
18.(1)已知线段a=2,b=9,求线段a,b的比例中项.
(2)已知x:y=4:3,求的值.
19.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
20.在△ABC中,D为边AC上一点.
(1)如图1,若,求证:;
(2)如图2,F为线段BD上一点,且满足
①当,,点F为BD中点时,求CD的长;
②延长CF交AB于E,当点D为AC中点且时,直接写出的值为 ▲ .
六、实践探究题
21.某校项目式学习小组开展项目活动,过程如下:
项目主题:测量旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
方案一 方案二 …
测量工具 标杆,皮尺 自制直角三角板硬纸板,皮尺 …
测量示意图 说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上. 说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上.
测量数据 B,D之间的距离 16.8m B,D之间的距离 16.8m …
D,F之间的距离 1.35m EF的长度 0.50m …
EF的长度 2.60m CE的长度 0.75m …
… …
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
答案解析部分
1.【答案】B
【知识点】相似多边形
2.【答案】A
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】B
【知识点】比例线段
4.【答案】A
【知识点】相似三角形的性质
5.【答案】A
【知识点】三角形的中位线定理
6.【答案】(答案不唯一)
【知识点】相似三角形的判定
7.【答案】1∶2
【知识点】相似三角形的性质
8.【答案】
【知识点】相似三角形的判定与性质
9.【答案】
【知识点】直角三角形斜边上的中线
10.【答案】5.95
【知识点】相似三角形的应用
11.【答案】①②④
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
12.【答案】(1)解:∵ ,
∴设 ,
则 ,
∴ ;
(2)解:
【知识点】比例的性质
13.【答案】12米
【知识点】相似三角形的应用
14.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
15.【答案】解:∵△ADE∽△ABC,
∴,
∵DE=8,BC=24,CD=18,AD=6,
∴AC=AD+CD=24,
∴AE=8,AB=18,
∴BE=AB-AE=10.
【知识点】相似三角形的性质
16.【答案】
【知识点】相似三角形的判定与性质
17.【答案】(1)解:将点代入得,,,
∴抛物线解析式为
,
∴抛物线的顶点坐标为;
(2)解:如下图,点与点是关于直线成轴对称,根据其性质有,,
当点、点、点共线时,为最小值,即为的最小值,
由抛物线解析式为,可得点坐标为,点坐标为,对称轴为,
设直线的解释为,
将点,点,代入得,,解得,
∴直线的解析式为,联立方程,
,解得
∴当的值最小时,点的坐标为.
【知识点】二次函数-动态几何问题
18.【答案】(1)解:设线段x是线段a,b的比例中项,
∵a=3,b=6,
x2=3×6=18,
x=(负值舍去).
∴线段a,b的比例中项是3.
(2)解:设x=4k,y=3k,
∴==.
【知识点】比例的性质;比例线段
19.【答案】(1)解:如图1中,∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD= ∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线
(2)解:①当AD=CD时,如图2,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
②当AD=AC时,如图3中,∠ACD=∠ADC= =66°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°.
③当AC=CD时,如图4中,∠ADC=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍弃.
∴∠ACB=96°或114°.
(3)解:由已知AC=AD=2,
∵△BCD∽△BAC,
∴ ,设BD=x,
∴( )2=x(x+2),
∵x>0,
∴x= ﹣1,
∵△BCD∽△BAC,
∴ = = ,
∴CD= ×2= ﹣
【知识点】相似三角形的判定与性质
20.【答案】(1)证明:∵,∠A=∠A,
∴△ABD∽△ACB,
∴,
∴
(2)解:①过点F作FM∥AB,交AC于M,
∴∠MFD=∠ABD,
∵,
∴∠MFD=∠MCF,
∵∠FMD=∠CMF,
∴△FMD∽△CMF,
∴,
∵FM∥AB,点F为BD中点,
∴FM是△ABD的中位线,
∴,AM=MD,
设AM=MD=x,
∴,
解得或(舍去),
∴CD=AC-AD=;
②
【知识点】相似三角形的判定与性质
21.【答案】解:方案一:过C作CH∥BD交EF于Q,交AB于H,
则四边形CDFQ,四边形CDBH都是矩形,
∴CQ=DF=1.35m,CH=BD=16.8m,
∵EQ∥AH,
∴
∵
∴△CEQ∽△CAH,
∴,
即:,
解得:AB=12.9m;
方案二:(1)∵∠ACG=∠ACG,∠CGA=∠AEF=90°.
∴△CEF∽△CGA,
∴,
即:,
解得:AB=12.9m;
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
