【沪科版九上同步练习】23.1 锐角的三角函数(含答案)
文档属性
| 名称 | 【沪科版九上同步练习】23.1 锐角的三角函数(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 19.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
23.1锐角的三角函数
一、单选题
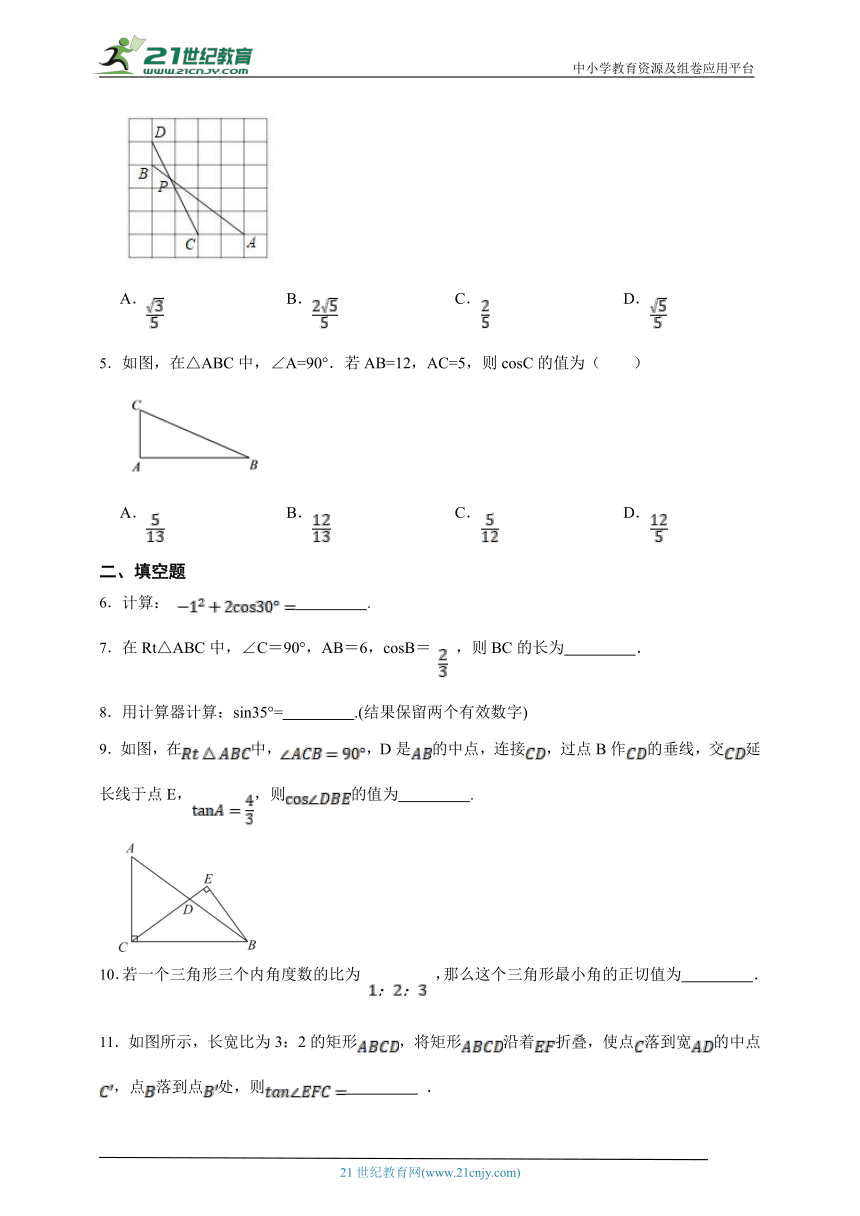
1.三角形在正方形网格纸中的位置如图所示.则的值是( )
A. B. C. D.
2.如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则cosA的值为( )
A. B. C. D.
3.如图,在小正方形网格中, 的三个顶点均在格点上,则 的值为( )
A. B. C. D.
4.如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
5.如图,在△ABC中,∠A=90°.若AB=12,AC=5,则cosC的值为( )
A. B. C. D.
二、填空题
6.计算: .
7.在Rt△ABC中,∠C=90°,AB=6,cosB= ,则BC的长为 .
8.用计算器计算:sin35°= .(结果保留两个有效数字)
9.如图,在中,,D是的中点,连接,过点B作的垂线,交延长线于点E,,则的值为 .
10.若一个三角形三个内角度数的比为 ,那么这个三角形最小角的正切值为 .
11.如图所示,长宽比为3:2的矩形,将矩形沿着折叠,使点落到宽的中点,点落到点处,则 .
三、计算题
12.计算:.
13.计算:
(1)2sin60°-|1-|-(-1)2021-2-2 .
(2)先化简,再求值: ,从1,2,3这三个数中选择一个你认为适合的x代入求值.
14.计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣ |
(2)先化简,再求值:( ﹣ )÷ ,其中x=2 ,y= .
四、解答题
15.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
16.先化简,再求值: ÷(x﹣2+ ),其中x=( )0+( )﹣1cos60°.
17.如图1,△ABC中,∠ACB=90°,AC=3,BC=4.P为斜边AB上的一动点(不包含A,B两端点),以CP为对称轴将△ACP翻折得到△A'CP,连结BA'.
(1)如图2,当CP⊥AB时,求BA'的长.
(2)当翻折得到的△A'CP中有一边与AB垂直时,求BA'的长.
五、综合题
18.在锐角△ABC中,AD与CE分别是边BC与AB的高,AB=12,BC=16,S△ABC=48,
求:
(1)角B的度数;
(2)tanC的值.
19.如图,已知是的直径,弦与相交于点E,.
(1)求的值;
(2)求点A到弦的距离.
20.如图1,在 中, ,边 ,点 分别在线段 上,将 沿直线 翻折,点C的对应点是点 ;
(1)当 分别是边 的中点时,求出 的长度;
(2)若 ,点 到线段 的最短距离是 ;
(3)如图2,当点 在落在边 上时,
①点 运动的路程长度是 ▲ ;
②当 时,求出 的长度.
六、实践探究题
21.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β) .利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°) 2 .
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题
(1)求sin75°;
(2)如图,边长为2的正 ABC沿直线滚动设当 ABC滚动240°时,C点的位置在 ,当 ABC滚动480°时,A点的位置在 .
①求tan∠ 的值;
②试确定 的度数.
答案解析部分
1.【答案】C
【知识点】锐角三角函数的定义
2.【答案】B
【知识点】锐角三角函数的定义
3.【答案】A
【知识点】勾股定理;锐角三角函数的定义
4.【答案】B
【知识点】平行线的性质;勾股定理;勾股定理的逆定理;锐角三角函数的定义
5.【答案】A
【知识点】勾股定理;锐角三角函数的定义
6.【答案】
【知识点】实数的运算;求特殊角的三角函数值
7.【答案】4
【知识点】锐角三角函数的定义
8.【答案】0.57
【知识点】计算器—三角函数
9.【答案】
【知识点】相似三角形的判定与性质;锐角三角函数的定义
10.【答案】
【知识点】三角形内角和定理;锐角三角函数的定义
11.【答案】3
【知识点】矩形的判定与性质;翻折变换(折叠问题);相似三角形的判定与性质;锐角三角函数的定义;三角形全等的判定-ASA
12.【答案】解:原式.
【知识点】实数的运算;求特殊角的三角函数值
13.【答案】(1)解:原式
·
(2)解:
,
,
, ,
或3,
当 时,原式 .
【知识点】实数的运算;分式的化简求值;求特殊角的三角函数值
14.【答案】(1)解: +cos245°﹣(﹣2)﹣1﹣|﹣ |
=0.2+
=0.2+
=0.7;
(2)解:( ﹣ )÷
=
=
=
=
= ,
当x=2 ,y= 时,原式= .
【知识点】实数的运算;分式的化简求值;负整数指数幂;求特殊角的三角函数值
15.【答案】解:过点A作AH⊥BC于H,∵S△ABC=27,∴ ,∴AH=6,∵AB=10,∴BH= = =8,∴tanB= = = .
【知识点】三角形的面积;勾股定理;锐角三角函数的定义
16.【答案】解:原式= ÷
=
= ,
当x=1+2× =2时,原式= .
【知识点】分式的化简求值;求特殊角的三角函数值
17.【答案】(1)解:如图2,当CP⊥AB时,
在中,
∴
在中,
在中,
∴
∵以CP为对称轴将△ACP翻折得到△A'CP,
∴
∵
∴
(2)解;①当时,
由(1)得:
②当时,设A'C⊥AB于点D,如图3:
∴
由(1)得:
∴
∵
∴
∴
③当时,如图4:
∴
∵以CP为对称轴将△ACP翻折得到△A'CP,
∴
作CD⊥AB于点D,则
∴
∴
∴
∴
综上所述,BA'的长为 或 或 .
【知识点】勾股定理;翻折变换(折叠问题);锐角三角函数的定义
18.【答案】(1)解:由题意可知:S△ABC= BC AD=48,BC=16,
∴AD=6,
在Rt△ABD中,
AB=12,
∴BD=6 ,sinB= = ,
∴∠B=30°
(2)解:∵BC=16,BD=6 ,
∴CD=16﹣6 ,
在Rt△ACD中,
CD=16﹣6 ,AD=6,
∴tanC= = .
【知识点】三角形的面积;锐角三角函数的定义
19.【答案】(1)解:如图,连接 ,过点O作 ,
∵ 是 的直径, ,
∴ , ,
∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ , ,
∴
(2)解:过点A作 ,
∴ ,
∴ ,
∴ ,
由(1)得 , ,
∴ ,
∴ ,
∴求点A到弦 的距离为6.
【知识点】等腰三角形的性质;勾股定理;相似三角形的判定与性质;锐角三角函数的定义
20.【答案】(1)解:设MN交 于O
∵M、N分别为AC、BC的中点
∴AM=CM,CN=BN
∴MN∥AB(中位线定理),
∵ ,
∴MN垂直平分
∴ ,
∴ 且点 落在AB上
∵∠C=90°
∴
∵
∴
(2)
(3)解:①4;
②如图3-3中,过点M作ME⊥AB于E,过点N作NF⊥AB于F,设CN=x,则BN=8-x,
∵ ,
∴ ,
∵ ,
∴
∴
∴ ,
∵
∴
∴
由翻折的性质得:
∴
∵
∴
∴
∴
∴
解得
经检验 是分式方程的解
∴
【知识点】线段垂直平分线的性质;翻折变换(折叠问题);相似三角形的判定与性质;锐角三角函数的定义;三角形的中位线定理
21.【答案】(1) sin(α+β)=sinαcosβ+cosαsinβ
(2)过点 作 于 ,过 作 于 ,过 作 于 ,如图
是等边三角形
,
② tan(α+β)
【知识点】等边三角形的性质;锐角三角函数的定义;求特殊角的三角函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
23.1锐角的三角函数
一、单选题
1.三角形在正方形网格纸中的位置如图所示.则的值是( )
A. B. C. D.
2.如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则cosA的值为( )
A. B. C. D.
3.如图,在小正方形网格中, 的三个顶点均在格点上,则 的值为( )
A. B. C. D.
4.如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
5.如图,在△ABC中,∠A=90°.若AB=12,AC=5,则cosC的值为( )
A. B. C. D.
二、填空题
6.计算: .
7.在Rt△ABC中,∠C=90°,AB=6,cosB= ,则BC的长为 .
8.用计算器计算:sin35°= .(结果保留两个有效数字)
9.如图,在中,,D是的中点,连接,过点B作的垂线,交延长线于点E,,则的值为 .
10.若一个三角形三个内角度数的比为 ,那么这个三角形最小角的正切值为 .
11.如图所示,长宽比为3:2的矩形,将矩形沿着折叠,使点落到宽的中点,点落到点处,则 .
三、计算题
12.计算:.
13.计算:
(1)2sin60°-|1-|-(-1)2021-2-2 .
(2)先化简,再求值: ,从1,2,3这三个数中选择一个你认为适合的x代入求值.
14.计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣ |
(2)先化简,再求值:( ﹣ )÷ ,其中x=2 ,y= .
四、解答题
15.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
16.先化简,再求值: ÷(x﹣2+ ),其中x=( )0+( )﹣1cos60°.
17.如图1,△ABC中,∠ACB=90°,AC=3,BC=4.P为斜边AB上的一动点(不包含A,B两端点),以CP为对称轴将△ACP翻折得到△A'CP,连结BA'.
(1)如图2,当CP⊥AB时,求BA'的长.
(2)当翻折得到的△A'CP中有一边与AB垂直时,求BA'的长.
五、综合题
18.在锐角△ABC中,AD与CE分别是边BC与AB的高,AB=12,BC=16,S△ABC=48,
求:
(1)角B的度数;
(2)tanC的值.
19.如图,已知是的直径,弦与相交于点E,.
(1)求的值;
(2)求点A到弦的距离.
20.如图1,在 中, ,边 ,点 分别在线段 上,将 沿直线 翻折,点C的对应点是点 ;
(1)当 分别是边 的中点时,求出 的长度;
(2)若 ,点 到线段 的最短距离是 ;
(3)如图2,当点 在落在边 上时,
①点 运动的路程长度是 ▲ ;
②当 时,求出 的长度.
六、实践探究题
21.阅读材料:关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ,tan(α+β) .利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和(差),如tan75°=tan(30°+45°) 2 .
问题解决:根据以上阅读材料,请选择适当的公式解答下列问题
(1)求sin75°;
(2)如图,边长为2的正 ABC沿直线滚动设当 ABC滚动240°时,C点的位置在 ,当 ABC滚动480°时,A点的位置在 .
①求tan∠ 的值;
②试确定 的度数.
答案解析部分
1.【答案】C
【知识点】锐角三角函数的定义
2.【答案】B
【知识点】锐角三角函数的定义
3.【答案】A
【知识点】勾股定理;锐角三角函数的定义
4.【答案】B
【知识点】平行线的性质;勾股定理;勾股定理的逆定理;锐角三角函数的定义
5.【答案】A
【知识点】勾股定理;锐角三角函数的定义
6.【答案】
【知识点】实数的运算;求特殊角的三角函数值
7.【答案】4
【知识点】锐角三角函数的定义
8.【答案】0.57
【知识点】计算器—三角函数
9.【答案】
【知识点】相似三角形的判定与性质;锐角三角函数的定义
10.【答案】
【知识点】三角形内角和定理;锐角三角函数的定义
11.【答案】3
【知识点】矩形的判定与性质;翻折变换(折叠问题);相似三角形的判定与性质;锐角三角函数的定义;三角形全等的判定-ASA
12.【答案】解:原式.
【知识点】实数的运算;求特殊角的三角函数值
13.【答案】(1)解:原式
·
(2)解:
,
,
, ,
或3,
当 时,原式 .
【知识点】实数的运算;分式的化简求值;求特殊角的三角函数值
14.【答案】(1)解: +cos245°﹣(﹣2)﹣1﹣|﹣ |
=0.2+
=0.2+
=0.7;
(2)解:( ﹣ )÷
=
=
=
=
= ,
当x=2 ,y= 时,原式= .
【知识点】实数的运算;分式的化简求值;负整数指数幂;求特殊角的三角函数值
15.【答案】解:过点A作AH⊥BC于H,∵S△ABC=27,∴ ,∴AH=6,∵AB=10,∴BH= = =8,∴tanB= = = .
【知识点】三角形的面积;勾股定理;锐角三角函数的定义
16.【答案】解:原式= ÷
=
= ,
当x=1+2× =2时,原式= .
【知识点】分式的化简求值;求特殊角的三角函数值
17.【答案】(1)解:如图2,当CP⊥AB时,
在中,
∴
在中,
在中,
∴
∵以CP为对称轴将△ACP翻折得到△A'CP,
∴
∵
∴
(2)解;①当时,
由(1)得:
②当时,设A'C⊥AB于点D,如图3:
∴
由(1)得:
∴
∵
∴
∴
③当时,如图4:
∴
∵以CP为对称轴将△ACP翻折得到△A'CP,
∴
作CD⊥AB于点D,则
∴
∴
∴
∴
综上所述,BA'的长为 或 或 .
【知识点】勾股定理;翻折变换(折叠问题);锐角三角函数的定义
18.【答案】(1)解:由题意可知:S△ABC= BC AD=48,BC=16,
∴AD=6,
在Rt△ABD中,
AB=12,
∴BD=6 ,sinB= = ,
∴∠B=30°
(2)解:∵BC=16,BD=6 ,
∴CD=16﹣6 ,
在Rt△ACD中,
CD=16﹣6 ,AD=6,
∴tanC= = .
【知识点】三角形的面积;锐角三角函数的定义
19.【答案】(1)解:如图,连接 ,过点O作 ,
∵ 是 的直径, ,
∴ , ,
∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ , ,
∴
(2)解:过点A作 ,
∴ ,
∴ ,
∴ ,
由(1)得 , ,
∴ ,
∴ ,
∴求点A到弦 的距离为6.
【知识点】等腰三角形的性质;勾股定理;相似三角形的判定与性质;锐角三角函数的定义
20.【答案】(1)解:设MN交 于O
∵M、N分别为AC、BC的中点
∴AM=CM,CN=BN
∴MN∥AB(中位线定理),
∵ ,
∴MN垂直平分
∴ ,
∴ 且点 落在AB上
∵∠C=90°
∴
∵
∴
(2)
(3)解:①4;
②如图3-3中,过点M作ME⊥AB于E,过点N作NF⊥AB于F,设CN=x,则BN=8-x,
∵ ,
∴ ,
∵ ,
∴
∴
∴ ,
∵
∴
∴
由翻折的性质得:
∴
∵
∴
∴
∴
∴
解得
经检验 是分式方程的解
∴
【知识点】线段垂直平分线的性质;翻折变换(折叠问题);相似三角形的判定与性质;锐角三角函数的定义;三角形的中位线定理
21.【答案】(1) sin(α+β)=sinαcosβ+cosαsinβ
(2)过点 作 于 ,过 作 于 ,过 作 于 ,如图
是等边三角形
,
② tan(α+β)
【知识点】等边三角形的性质;锐角三角函数的定义;求特殊角的三角函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
