2023-2024学年北京六十六中高二(下)质检数学试卷(6月份)(含答案)
文档属性
| 名称 | 2023-2024学年北京六十六中高二(下)质检数学试卷(6月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 18:12:07 | ||
图片预览


文档简介
2023-2024学年北京六十六中高二(下)质检数学试卷(6月份)
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.函数在处的瞬时变化率为( )
A. B. C. D.
2.若、、成等差数列,则( )
A. B. C. D.
3.已知直线是曲线的切线,则切点坐标为( )
A. B. C. D.
4.已知某一离散型随机变量的分布列,且,则的值为( )
A. B. C. D.
5.已知函数,为的导函数,则( )
A. B.
C. D.
6.等差数列中,设前项和为,,则等于( )
A. B. C. D.
7.某人射击一次击中目标的概率为,此人射击次恰有两次击中目标的概率为( )
A. B. C. D.
8.记为等比数列的前项和,若,,则( )
A. B. C. D.
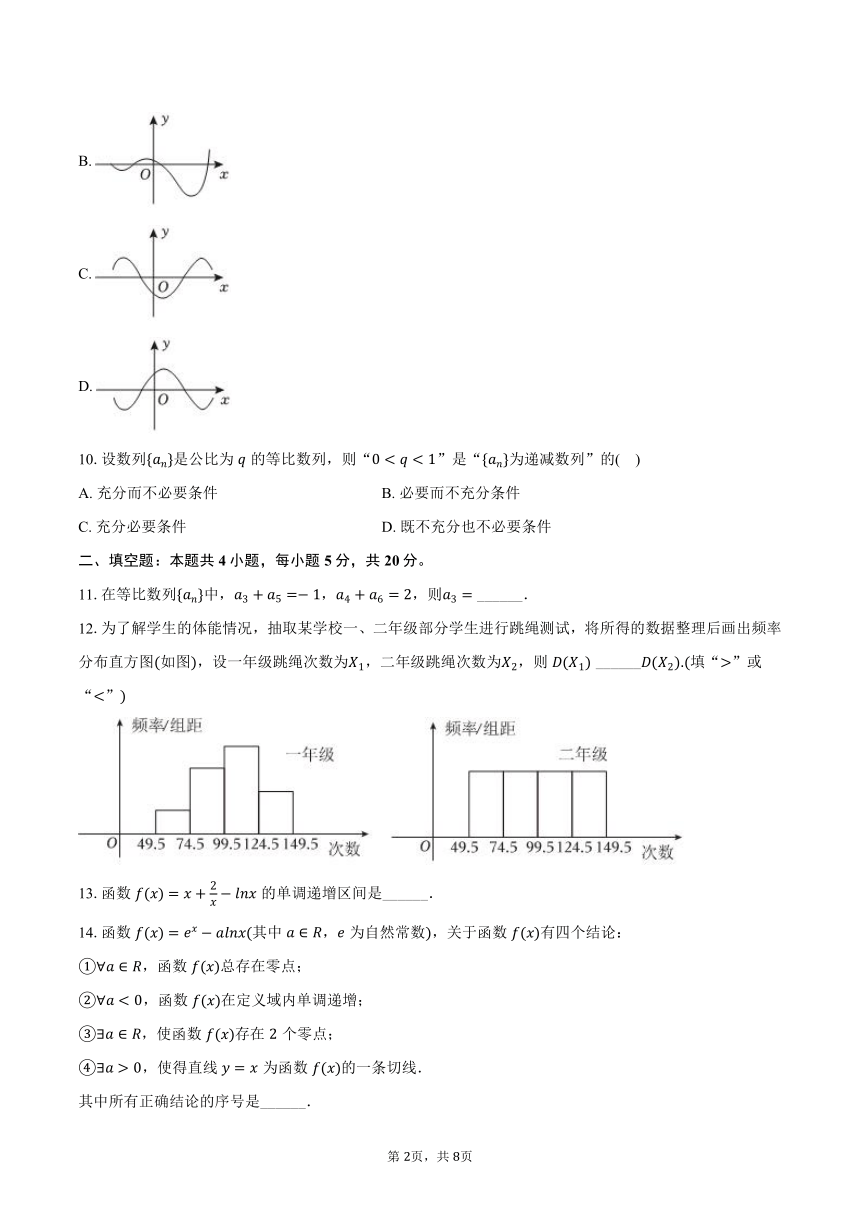
9.函数的导函数的图像如图所示,则函数的图像可能是( )
A.
B.
C.
D.
10.设数列是公比为的等比数列,则“”是“为递减数列”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
二、填空题:本题共4小题,每小题5分,共20分。
11.在等比数列中,,,则 ______.
12.为了解学生的体能情况,抽取某学校一、二年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图如图,设一年级跳绳次数为,二年级跳绳次数为,则 ______填“”或“”
13.函数的单调递增区间是______.
14.函数其中,为自然常数,关于函数有四个结论:
,函数总存在零点;
,函数在定义域内单调递增;
,使函数存在个零点;
,使得直线为函数的一条切线.
其中所有正确结论的序号是______.
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设函数.
Ⅰ求曲线在点处的切线方程;
Ⅱ求在区间上的最大值和最小值.
16.本小题分
据世界田联官方网站消息,原定于年月、日在中国广州举办的世界田联接力赛延期至年月至月举行据了解,甲、乙、丙三支队伍将会参加年月至月在广州举行的米接力的角逐接力赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进入决赛已知甲队在预赛和半决赛中获胜的概率分别为和;乙队在预赛和半决赛中获胜的概率分别为和;丙队在预赛和半决赛中获胜的概率分别为和.
甲、乙、丙三队中,谁进入决赛的可能性最大;
设甲、乙、丙三队中进入决赛的队伍数为,求的分布列.
17.本小题分
设为等差数列的前项和,,.
Ⅰ求数列的通项公式;
Ⅱ求;
Ⅲ若,,成等比数列,求的值.
18.本小题分
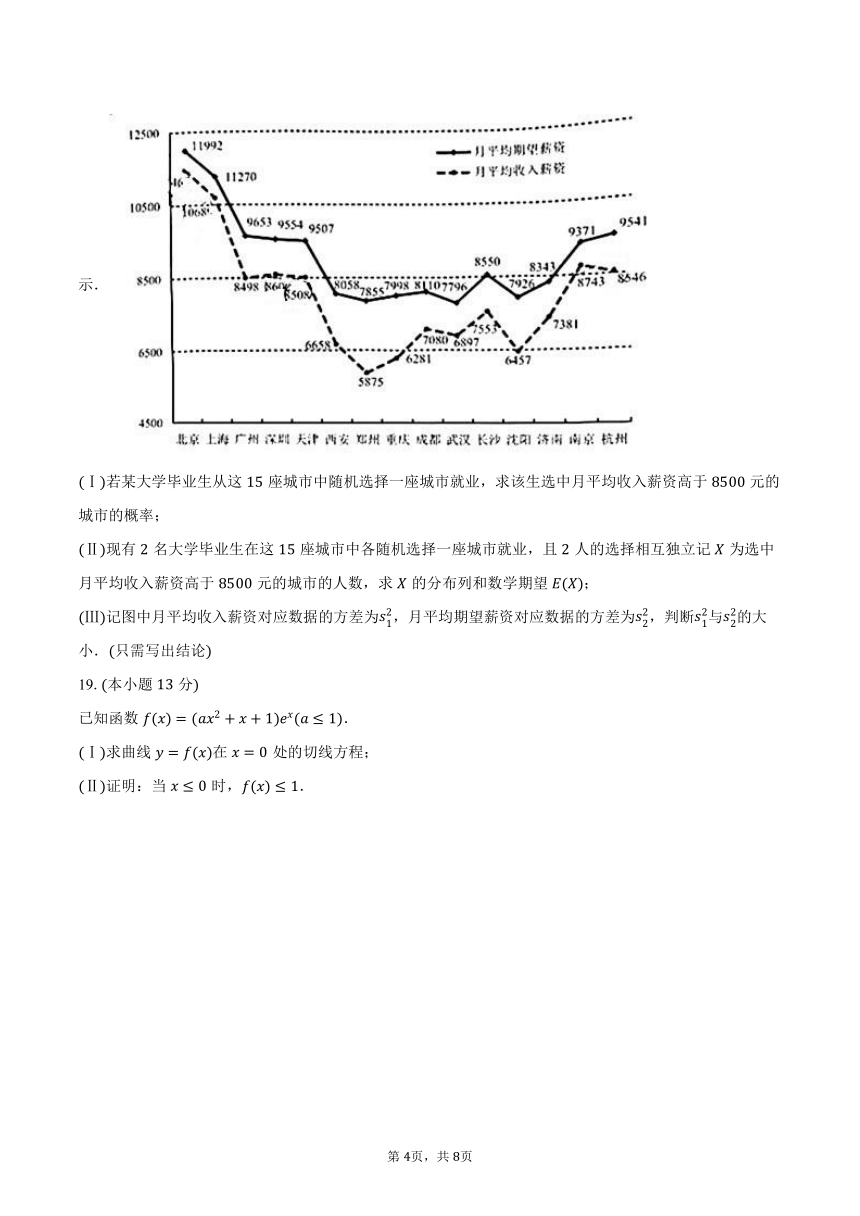
随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如图所示.
Ⅰ若某大学毕业生从这座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于元的城市的概率;
Ⅱ现有名大学毕业生在这座城市中各随机选择一座城市就业,且人的选择相互独立记为选中月平均收入薪资高于元的城市的人数,求的分布列和数学期望;
Ⅲ记图中月平均收入薪资对应数据的方差为,月平均期望薪资对应数据的方差为,判断与的大小.只需写出结论
19.本小题分
已知函数.
Ⅰ求曲线在处的切线方程;
Ⅱ证明:当时,.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.解:Ⅰ 由题意知,,即切点为,又,所以,
所以曲线在点处的切线方程为:,即.
Ⅱ令,,解得,.
当时,可得,即的单调递减区间为,
当或,可得,所以函数单调递增区间为,.
所以的极大值点为,,
因为,,
所以函数的最大值为,最小值为.
16.解:甲队进入决赛的概率为,
乙队进入决赛的概率为,
丙队进入决赛的概率为,
显然乙队进入决赛的概率最大,所以乙进入决赛的可能性最大.
由可知:甲、乙、丙三队进入决赛的概率分别为,
的可能取值为,,,,
,,,,
故的分布列为:
17.解:Ⅰ由题意得,
解得;
故的通项公式为;
Ⅱ由Ⅰ知,;
因为,,成等比数列,
所以,
所以,
即,
又因为,则解得.
18.解:Ⅰ设该生该月平均收入薪资高于元的城市为事件,
座城市中月收薪资高于元的有个,
该生选中月平均收入薪资高于元的城市的概率.
Ⅱ由Ⅰ知选中平均薪资高于元的城市的概率为,
低于元的概率为,
,
,
,
,
的分布列为:
.
Ⅲ.
19.解:Ⅰ因为,所以,,
所以在处的切线方程为:,即;
Ⅱ证明:,
当时,,
若,,单调递增,
若时,,单调递减,
当时,,单调递增,
又,,
所以恒成立;
当时,,所以在上单调递增,
又因为,所以恒成立;
时,,
若,,单调递增,
若,,单调递减,
若,,单调递增,
且,,所以恒成立;
当时,,,
若,,单调递减,
若,,单调递增,
且时,,所以恒成立;
当时,,
若,,单调递减,
若,,单调递增,
且,又时,,
所以时,,所以恒成立;
综上可知:当时,.
第1页,共1页
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.函数在处的瞬时变化率为( )
A. B. C. D.
2.若、、成等差数列,则( )
A. B. C. D.
3.已知直线是曲线的切线,则切点坐标为( )
A. B. C. D.
4.已知某一离散型随机变量的分布列,且,则的值为( )
A. B. C. D.
5.已知函数,为的导函数,则( )
A. B.
C. D.
6.等差数列中,设前项和为,,则等于( )
A. B. C. D.
7.某人射击一次击中目标的概率为,此人射击次恰有两次击中目标的概率为( )
A. B. C. D.
8.记为等比数列的前项和,若,,则( )
A. B. C. D.
9.函数的导函数的图像如图所示,则函数的图像可能是( )
A.
B.
C.
D.
10.设数列是公比为的等比数列,则“”是“为递减数列”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
二、填空题:本题共4小题,每小题5分,共20分。
11.在等比数列中,,,则 ______.
12.为了解学生的体能情况,抽取某学校一、二年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图如图,设一年级跳绳次数为,二年级跳绳次数为,则 ______填“”或“”
13.函数的单调递增区间是______.
14.函数其中,为自然常数,关于函数有四个结论:
,函数总存在零点;
,函数在定义域内单调递增;
,使函数存在个零点;
,使得直线为函数的一条切线.
其中所有正确结论的序号是______.
三、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设函数.
Ⅰ求曲线在点处的切线方程;
Ⅱ求在区间上的最大值和最小值.
16.本小题分
据世界田联官方网站消息,原定于年月、日在中国广州举办的世界田联接力赛延期至年月至月举行据了解,甲、乙、丙三支队伍将会参加年月至月在广州举行的米接力的角逐接力赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进入决赛已知甲队在预赛和半决赛中获胜的概率分别为和;乙队在预赛和半决赛中获胜的概率分别为和;丙队在预赛和半决赛中获胜的概率分别为和.
甲、乙、丙三队中,谁进入决赛的可能性最大;
设甲、乙、丙三队中进入决赛的队伍数为,求的分布列.
17.本小题分
设为等差数列的前项和,,.
Ⅰ求数列的通项公式;
Ⅱ求;
Ⅲ若,,成等比数列,求的值.
18.本小题分
随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如图所示.
Ⅰ若某大学毕业生从这座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于元的城市的概率;
Ⅱ现有名大学毕业生在这座城市中各随机选择一座城市就业,且人的选择相互独立记为选中月平均收入薪资高于元的城市的人数,求的分布列和数学期望;
Ⅲ记图中月平均收入薪资对应数据的方差为,月平均期望薪资对应数据的方差为,判断与的大小.只需写出结论
19.本小题分
已知函数.
Ⅰ求曲线在处的切线方程;
Ⅱ证明:当时,.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.解:Ⅰ 由题意知,,即切点为,又,所以,
所以曲线在点处的切线方程为:,即.
Ⅱ令,,解得,.
当时,可得,即的单调递减区间为,
当或,可得,所以函数单调递增区间为,.
所以的极大值点为,,
因为,,
所以函数的最大值为,最小值为.
16.解:甲队进入决赛的概率为,
乙队进入决赛的概率为,
丙队进入决赛的概率为,
显然乙队进入决赛的概率最大,所以乙进入决赛的可能性最大.
由可知:甲、乙、丙三队进入决赛的概率分别为,
的可能取值为,,,,
,,,,
故的分布列为:
17.解:Ⅰ由题意得,
解得;
故的通项公式为;
Ⅱ由Ⅰ知,;
因为,,成等比数列,
所以,
所以,
即,
又因为,则解得.
18.解:Ⅰ设该生该月平均收入薪资高于元的城市为事件,
座城市中月收薪资高于元的有个,
该生选中月平均收入薪资高于元的城市的概率.
Ⅱ由Ⅰ知选中平均薪资高于元的城市的概率为,
低于元的概率为,
,
,
,
,
的分布列为:
.
Ⅲ.
19.解:Ⅰ因为,所以,,
所以在处的切线方程为:,即;
Ⅱ证明:,
当时,,
若,,单调递增,
若时,,单调递减,
当时,,单调递增,
又,,
所以恒成立;
当时,,所以在上单调递增,
又因为,所以恒成立;
时,,
若,,单调递增,
若,,单调递减,
若,,单调递增,
且,,所以恒成立;
当时,,,
若,,单调递减,
若,,单调递增,
且时,,所以恒成立;
当时,,
若,,单调递减,
若,,单调递增,
且,又时,,
所以时,,所以恒成立;
综上可知:当时,.
第1页,共1页
同课章节目录
