初中数学人教版七年级下册5.3.1平行线的性质教学设计(表格式)
文档属性
| 名称 | 初中数学人教版七年级下册5.3.1平行线的性质教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 65.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 00:00:00 | ||
图片预览

文档简介
教学设计
课 题 平行线的性质
课时安排 1课时 课前准备 彩色卡纸,磁石
教材内容 分 析 本节课内容属于《义务教育数学课程标准(2022年版)》中七年级下册“平行线的性质”相关内容.《平行线的性质》是继平行线的判定之后对有关平行线知识的进一步补充,同时也对后面学习命题、定理做好铺垫,因此本节课在这一章中起着承上启下的作用。
设计理念 教学过程中借助动手画一画量一量培养学生实际操作能力和动手能力。
学情分析 学生的知识技能基础:学生在小学时,已经初步了解了什么是平行线。在前面的学习中,已掌握平行线的相关判定,了解了平行与平行所产生的三类角之间的关系。 学生的活动经验基础:在前面的学习当中,学生已经掌握如何画已知直线的平行线。
教学目标 1、经历探索平行线性质的过程,初步掌握平行线的性质; 2、能用平行线的性质解决一些问题; 3、通过观察、操作、推理等活动,进一步发展学生的空间观念和推理能力。
教学重难点 教学重点:平行线的性质的探索及对性质的理解。 教学难点:有条理地表达与推理。
教学过程
教学环节(一) 师生活动 带领学生回顾平行线的判定:1、同位角相等,两直线平行。2、内错角相等,两直线平行。3、同旁内角互补,两直线平行。让学生明确平行线的判定是由角的数量关系推得直线的位置关系,提问:“那么反过来,如果已知直线的位置关系,那么我们能否推得角的数量关系呢?也就是说,当两条直线互相平行时,同位角、内错角、同旁内角又有怎样的数量关系呢?”抛出问题,揭示本堂课的主题:平行线的性质。
设计意图 通过复习平行线的判定引入课题,感受知识的延续性,为探索平行线的性质做铺垫。
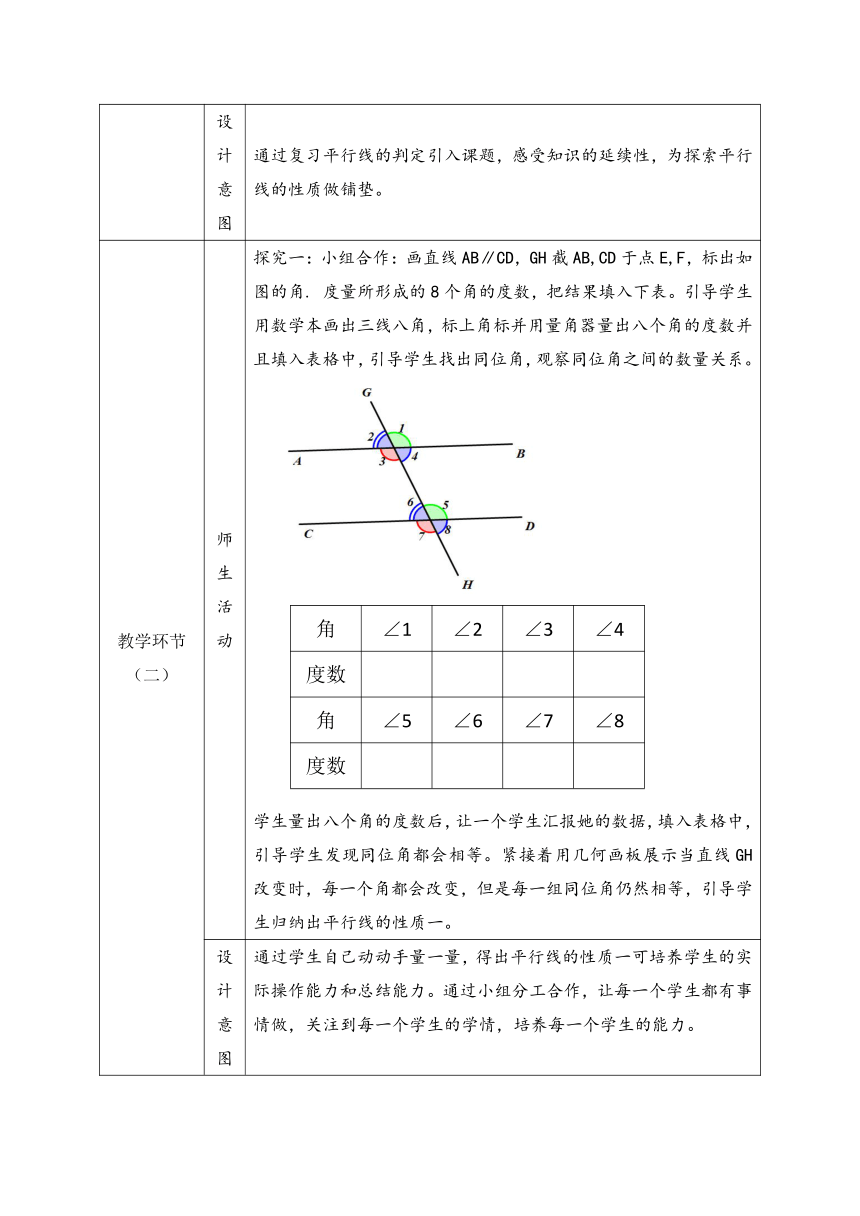
教学环节(二) 师生活动 探究一:小组合作:画直线AB∥CD,GH截AB,CD于点E,F,标出如图的角. 度量所形成的8个角的度数,把结果填入下表。引导学生用数学本画出三线八角,标上角标并用量角器量出八个角的度数并且填入表格中,引导学生找出同位角,观察同位角之间的数量关系。 角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数
学生量出八个角的度数后,让一个学生汇报她的数据,填入表格中,引导学生发现同位角都会相等。紧接着用几何画板展示当直线GH改变时,每一个角都会改变,但是每一组同位角仍然相等,引导学生归纳出平行线的性质一。
设计意图 通过学生自己动动手量一量,得出平行线的性质一可培养学生的实际操作能力和总结能力。通过小组分工合作,让每一个学生都有事情做,关注到每一个学生的学情,培养每一个学生的能力。
教学环节 (三) 师生活动 归纳出性质一,把准备好的蓝色卡纸性质一贴到黑板上,引导学生朗读性质一,并用文字和符号语言进行描述。探究二:提问:“同学们,现在我们知道当两直线平行时,同位角会相等,那内错角又有怎样的数量关系呢?”引导学生对此问题进行推理。学生会发现已知条件是两直线平行,于是得到同位角相等,再由对顶角相等进行等量代换得到内错角会相等,归纳出性质二。探究三:提问:“两条直线被第三条直线所截,会产生同位角,内错角,还有同旁内角,那当两直线平行时,同旁内角又有怎样的数量关系呢?”由性质二的推理过程可以类比推理得到性质三。
设计意图 通过类比推理引导学生总结出剩下两个性质,衔接流畅过渡自然,同时培养学生多角度思考问题的良好习惯,学生的表达能力和逻辑推理能力。
教学环节 (四) 师生活动 如图1,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么? 出示例题1,学生独立思考后引导学生利用平行线的三条性质进行求解。 如图2,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,请问梯形的另外两个角分别是多少度? 出示例题2,学生独立思考后提问:你求得的两个角度数是多少,理由是什么?这里强调隐形条件是梯形,梯形的上底下底会相互平行。 如图3,已知∠1=∠2,∠3=65°,求∠4的度数. 出示例题3,引导学生从已知条件∠1=∠2出发,由平行线的判定可以得到直线AB平行CD,然后结合平行线的性质进行突破。小结本道题是判定与性质的综合应用。
设计意图 例题讲解,考察学生对知识的掌握能力并且巩固本节课的知识点。
教学环节 (五) 师生活动 带领学生回顾本堂课的重难点,学生自己来说,第一,平行线的性质,第二,数学语言的表达,第三,转化的思想方法。
设计意图 课堂小结对本堂课进行了整合并形成结构化知识;提炼学科思想,渗透正确的情感态度与价值观。
板书设计 平行线的性质 一、性质 二、例题讲解
教学反思 整个环节比较完整,学生主观能动性很强,但在整堂课中信息技术的利用不够彻底。
课 题 平行线的性质
课时安排 1课时 课前准备 彩色卡纸,磁石
教材内容 分 析 本节课内容属于《义务教育数学课程标准(2022年版)》中七年级下册“平行线的性质”相关内容.《平行线的性质》是继平行线的判定之后对有关平行线知识的进一步补充,同时也对后面学习命题、定理做好铺垫,因此本节课在这一章中起着承上启下的作用。
设计理念 教学过程中借助动手画一画量一量培养学生实际操作能力和动手能力。
学情分析 学生的知识技能基础:学生在小学时,已经初步了解了什么是平行线。在前面的学习中,已掌握平行线的相关判定,了解了平行与平行所产生的三类角之间的关系。 学生的活动经验基础:在前面的学习当中,学生已经掌握如何画已知直线的平行线。
教学目标 1、经历探索平行线性质的过程,初步掌握平行线的性质; 2、能用平行线的性质解决一些问题; 3、通过观察、操作、推理等活动,进一步发展学生的空间观念和推理能力。
教学重难点 教学重点:平行线的性质的探索及对性质的理解。 教学难点:有条理地表达与推理。
教学过程
教学环节(一) 师生活动 带领学生回顾平行线的判定:1、同位角相等,两直线平行。2、内错角相等,两直线平行。3、同旁内角互补,两直线平行。让学生明确平行线的判定是由角的数量关系推得直线的位置关系,提问:“那么反过来,如果已知直线的位置关系,那么我们能否推得角的数量关系呢?也就是说,当两条直线互相平行时,同位角、内错角、同旁内角又有怎样的数量关系呢?”抛出问题,揭示本堂课的主题:平行线的性质。
设计意图 通过复习平行线的判定引入课题,感受知识的延续性,为探索平行线的性质做铺垫。
教学环节(二) 师生活动 探究一:小组合作:画直线AB∥CD,GH截AB,CD于点E,F,标出如图的角. 度量所形成的8个角的度数,把结果填入下表。引导学生用数学本画出三线八角,标上角标并用量角器量出八个角的度数并且填入表格中,引导学生找出同位角,观察同位角之间的数量关系。 角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数
学生量出八个角的度数后,让一个学生汇报她的数据,填入表格中,引导学生发现同位角都会相等。紧接着用几何画板展示当直线GH改变时,每一个角都会改变,但是每一组同位角仍然相等,引导学生归纳出平行线的性质一。
设计意图 通过学生自己动动手量一量,得出平行线的性质一可培养学生的实际操作能力和总结能力。通过小组分工合作,让每一个学生都有事情做,关注到每一个学生的学情,培养每一个学生的能力。
教学环节 (三) 师生活动 归纳出性质一,把准备好的蓝色卡纸性质一贴到黑板上,引导学生朗读性质一,并用文字和符号语言进行描述。探究二:提问:“同学们,现在我们知道当两直线平行时,同位角会相等,那内错角又有怎样的数量关系呢?”引导学生对此问题进行推理。学生会发现已知条件是两直线平行,于是得到同位角相等,再由对顶角相等进行等量代换得到内错角会相等,归纳出性质二。探究三:提问:“两条直线被第三条直线所截,会产生同位角,内错角,还有同旁内角,那当两直线平行时,同旁内角又有怎样的数量关系呢?”由性质二的推理过程可以类比推理得到性质三。
设计意图 通过类比推理引导学生总结出剩下两个性质,衔接流畅过渡自然,同时培养学生多角度思考问题的良好习惯,学生的表达能力和逻辑推理能力。
教学环节 (四) 师生活动 如图1,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么? 出示例题1,学生独立思考后引导学生利用平行线的三条性质进行求解。 如图2,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,请问梯形的另外两个角分别是多少度? 出示例题2,学生独立思考后提问:你求得的两个角度数是多少,理由是什么?这里强调隐形条件是梯形,梯形的上底下底会相互平行。 如图3,已知∠1=∠2,∠3=65°,求∠4的度数. 出示例题3,引导学生从已知条件∠1=∠2出发,由平行线的判定可以得到直线AB平行CD,然后结合平行线的性质进行突破。小结本道题是判定与性质的综合应用。
设计意图 例题讲解,考察学生对知识的掌握能力并且巩固本节课的知识点。
教学环节 (五) 师生活动 带领学生回顾本堂课的重难点,学生自己来说,第一,平行线的性质,第二,数学语言的表达,第三,转化的思想方法。
设计意图 课堂小结对本堂课进行了整合并形成结构化知识;提炼学科思想,渗透正确的情感态度与价值观。
板书设计 平行线的性质 一、性质 二、例题讲解
教学反思 整个环节比较完整,学生主观能动性很强,但在整堂课中信息技术的利用不够彻底。
