【沪科版九上同步练习】 第 23.章解直角三角形(能力提升)检测题
文档属性
| 名称 | 【沪科版九上同步练习】 第 23.章解直角三角形(能力提升)检测题 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
第 23.章解直角三角形(能力提升)检测题
一、填空题
1.已知在中,,,,那么的长是 .
2.定义一种运算,计算 .
3.在正方形网格中,∠AOB如图放置,则tan∠AOB的值为 .
4.如图,从航拍无人机A看一栋楼顶部B的仰角α为,看这栋楼底部C的俯角β为,无人机与楼的水平距离为,则这栋楼的高度为 .
5.如图,把一块直角三角板()的直角顶点放在坐标原点处,顶点在函数的图象上,顶点在函数的图象上,则= .
6.在直角坐标系中,已知 、 , ,在 的边上取两点 、 (点 是不同于点 的点),若以 、 、 为顶点的三角形与 全等,则符合条件的点 的坐标为 .
二、单选题
7.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶,则AC的长是( )
A.6米 B.12米 C.3米 D.6米
8.已知在中,,,,则的值为( )
A. B. C. D.
9.如图,在中,,定义:斜边与的对边的比叫做的余割,用“”表示.若该直角三角形的三边分别为a,b,c,则,那么下列说法正确的是( )
A. B. C. D.
10.如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
A. B. C. D.
11.在中,,,,那么下列各式中,正确的是( )
A. B. C. D.
三、解答题
12.如图,某游客在山脚下乘览车上山.导游告知,索道与水平线成角∠BAC为40°,览车速度为60米/分,11分钟到达山顶,请根据以上信息计算山的高度BC.
(精确到1米)(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84)
13.学生到工厂劳动实践,学习机械零件,零件的截面如图所示,已知四边形AEFD为矩形,点B,C分别在EF,DF上,∠ABC为90°,∠BAD=53°,AB=10cm,BC=6cm,求零件的截面面积.
参考数据:sin53°≈0.80,cos53°≈0.60.
14.如图,已知Rt△ABO,∠BAO=90°,以点O为坐标原点,OA所在直线为y轴,建立平面直角坐标系,AO=3,∠AOB=30°,将Rt△ABO沿OB翻折后,点A落在第一象限内的点D处.
(1)求D点坐标;
(2)若抛物线y=ax2+bx+3(a≠0)经过B、D两点,求此抛物线的表达式;
(3)若抛物线的顶点为E,它的对称轴与OB交于点F,点P为射线OB上一动点,过点P作y轴的平行线,交抛物线于点M.是否存在点P,使得以E、F、M、P为顶点的四边形为等腰梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
四、计算题
15.计算:
16.计算:
(1);
(2).
五、综合题
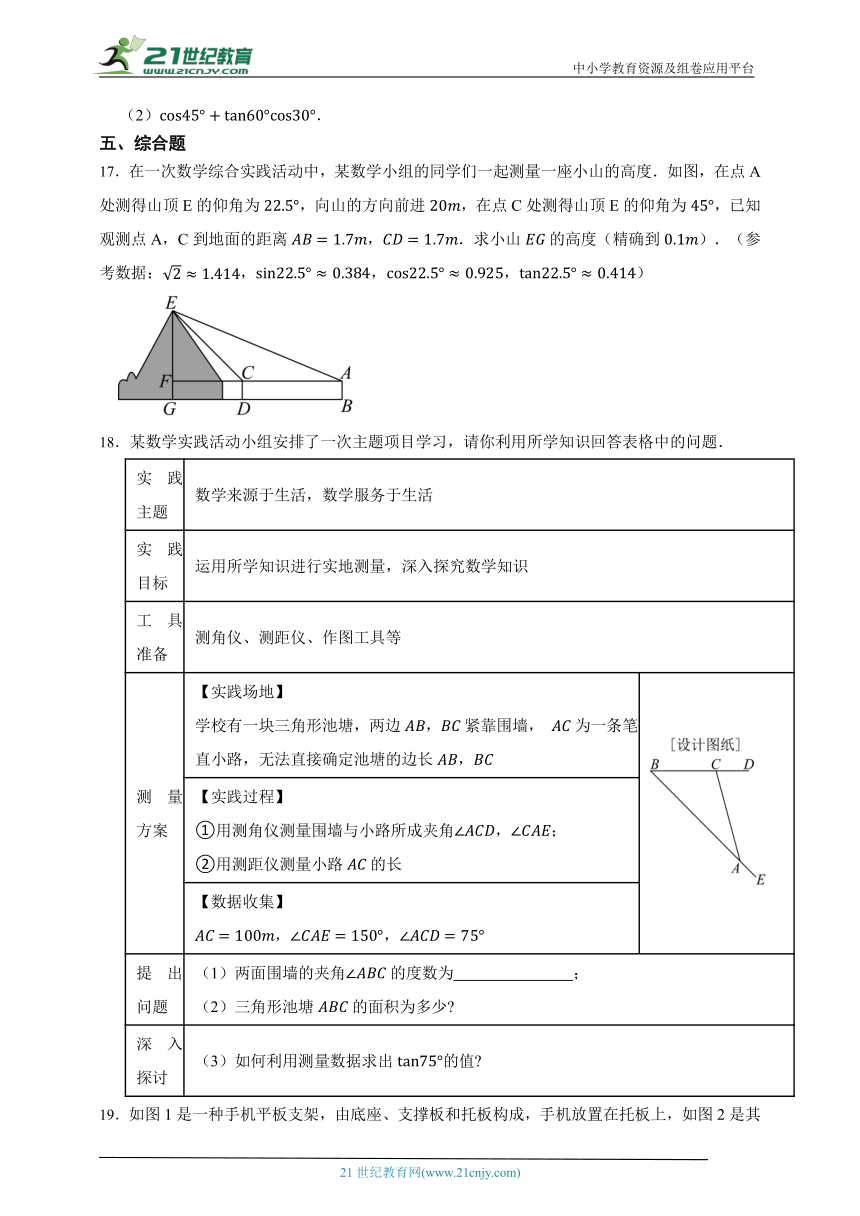
17.在一次数学综合实践活动中,某数学小组的同学们一起测量一座小山的高度.如图,在点A处测得山顶E的仰角为,向山的方向前进,在点C处测得山顶E的仰角为,已知观测点A,C到地面的距离,.求小山的高度(精确到).(参考数据:,,,)
18.某数学实践活动小组安排了一次主题项目学习,请你利用所学知识回答表格中的问题.
实践主题 数学来源于生活,数学服务于生活
实践目标 运用所学知识进行实地测量,深入探究数学知识
工具准备 测角仪、测距仪、作图工具等
测量方案 【实践场地】 学校有一块三角形池塘,两边,紧靠围墙, 为一条笔直小路,无法直接确定池塘的边长,
【实践过程】 ①用测角仪测量围墙与小路所成夹角,; ②用测距仪测量小路的长
【数据收集】 ,,
提出问题 (1)两面围墙的夹角的度数为 ; (2)三角形池塘的面积为多少
深入探讨 (3)如何利用测量数据求出的值
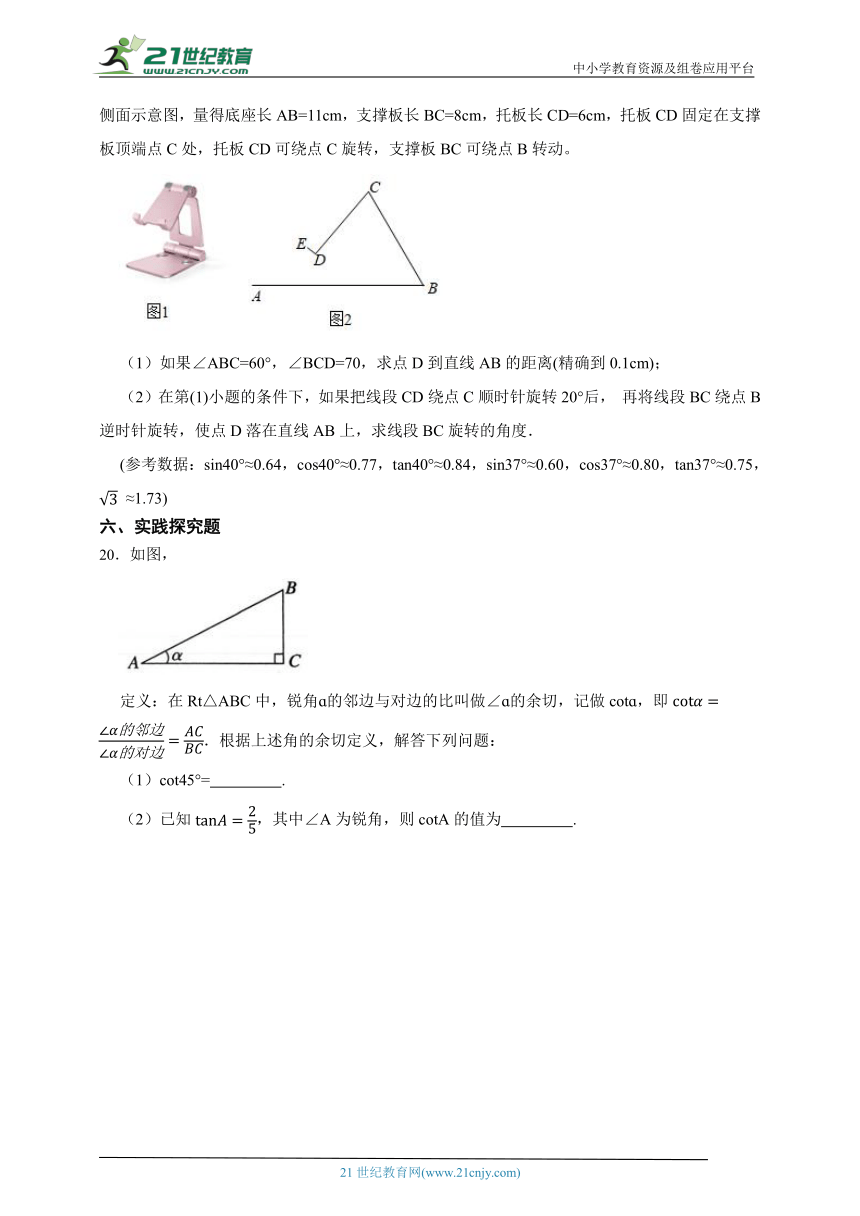
19.如图1是一种手机平板支架,由底座、支撑板和托板构成,手机放置在托板上,如图2是其侧面示意图,量得底座长AB=11cm,支撑板长BC=8cm,托板长CD=6cm,托板CD固定在支撑板顶端点C处,托板CD可绕点C旋转,支撑板BC可绕点B转动。
(1)如果∠ABC=60°,∠BCD=70,求点D到直线AB的距离(精确到0.1cm);
(2)在第(1)小题的条件下,如果把线段CD绕点C顺时针旋转20°后, 再将线段BC绕点B逆时针旋转,使点D落在直线AB上,求线段BC旋转的角度.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.73)
六、实践探究题
20.如图,
定义:在Rt△ABC中,锐角ɑ的邻边与对边的比叫做∠ɑ的余切,记做cotɑ,即.根据上述角的余切定义,解答下列问题:
(1)cot45°= .
(2)已知,其中∠A为锐角,则cotA的值为 .
答案解析部分
1.【答案】
【知识点】解直角三角形
2.【答案】
【知识点】求特殊角的三角函数值
3.【答案】2
【知识点】锐角三角函数的定义
4.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】3
【知识点】解直角三角形
6.【答案】 , , ,
【知识点】一次函数中的动态几何问题
7.【答案】D
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】锐角三角函数的定义
11.【答案】C
【知识点】锐角三角函数的定义
12.【答案】解:由题意可得:∠BAC=40°,AB=66米.
∵sin40°= ,∴BC≈0.64×660=422.4米≈422米.
答:山的高度BC约为422米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】解:∵∠BAD=53°;
∴∠EAB=37°;
∴∠EBA=53°;
∴AE=ABxsin∠EBA=10x0.8=8cm;
∴BE= cm;
∵∠ABC=90°;
∴∠CBF=37°;
∴∠BCF=53°;
∴BF=BCxsin∠BCF=6x0.8=4.8cm;
∴CF= 3.6cm;
=8x10.8- x8x6- x4.8x3.6
=53.76cm2
【知识点】矩形的性质;求特殊角的三角函数值
14.【答案】解:(1)过点D作DE⊥x轴于点E,如图(1).由翻折可知:DO=AO=3,∠AOB=∠BOD=30°,∴∠DOE=30°.∴DE=在Rt△COD中,由勾股定理,得OE=∴D(,)(2)在Rt△AOB中,AB=AO tan30°=3×=,∴B(,3).∵抛物线y=ax2+bx+3(a≠0)经过B(,3),D(,)两点,∴解得∴此抛物线表达式为y=﹣x2+x+3.(3)存在符合条件的点P,设P(x,y),作EH⊥PM于点H,FG⊥PM于点G,如图(2).∵E为抛物线y=﹣x2+x+3的顶点,∴E(,).设OB所在直线的表达式为y=kx,将点B(,3)代入,得k=,∴y=x.∵P在射线OB上,∴P(x,x),F(,).则H(x,)G(x,).∵M在抛物线上,M(x,﹣x2++3).要使四边形EFMP为等腰梯形,只需PH=GM.x﹣=﹣(﹣x2+x+3),即﹣x2+x+3+x=5.解得x1=2,x2=.∴P1点坐标为(2,6),P2点坐标为(,)与F重合,应舍去.∴P点坐标为(2,6).
【知识点】二次函数的实际应用-几何问题
15.【答案】
【知识点】求特殊角的三角函数值
16.【答案】(1)解:原式
=1.
(2)解:原式
.
【知识点】求特殊角的三角函数值
17.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
18.【答案】(1);(2);(3)
【知识点】解直角三角形的其他实际应用
19.【答案】(1)解:如图2,过D作DM⊥AB,交AB于点M,过点C作CN⊥AB于点N,垂足为N,过点D作DQ⊥CN交CB于点Q,垂足为F,
在Rt△CNB中,∠ABC=60°,BC=8cm,
∴CN=CB sin∠ABC=8×≈6.92(cm),
∵∠BCN=90°-60°=30°,又∵∠DCB=70°,
∴∠DCF=70°-30°=40°,
在Rt△DCF中,∠DCF=40°,CD=6cm,∴CF=CD cos40°≈6×0.77=4.62(cm),
∵∠DMN=∠MNF=∠NFD=90°,∴四边形MNFD是矩形,
∴DM=FN=CN-CF=6.92-4.62=2.3(cm),
即点D到直线AB的距离为2.3cm;
(2)解:把线段CD绕点C顺时针旋转20°后,∠C′=70°+20°=90°,如图,
∵BC=8cm,CD=6cm,
∴tan∠B=0.75,
∵tan37°≈0.75,
∴∠C′BD′=37°,
∵∠ABC=60°,
∴∠CBC′=60°-37°=23°,
答:线段BC旋转的角度为23°.
【知识点】解直角三角形
20.【答案】(1)1
(2)
【知识点】锐角三角函数的定义;等腰直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
第 23.章解直角三角形(能力提升)检测题
一、填空题
1.已知在中,,,,那么的长是 .
2.定义一种运算,计算 .
3.在正方形网格中,∠AOB如图放置,则tan∠AOB的值为 .
4.如图,从航拍无人机A看一栋楼顶部B的仰角α为,看这栋楼底部C的俯角β为,无人机与楼的水平距离为,则这栋楼的高度为 .
5.如图,把一块直角三角板()的直角顶点放在坐标原点处,顶点在函数的图象上,顶点在函数的图象上,则= .
6.在直角坐标系中,已知 、 , ,在 的边上取两点 、 (点 是不同于点 的点),若以 、 、 为顶点的三角形与 全等,则符合条件的点 的坐标为 .
二、单选题
7.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶,则AC的长是( )
A.6米 B.12米 C.3米 D.6米
8.已知在中,,,,则的值为( )
A. B. C. D.
9.如图,在中,,定义:斜边与的对边的比叫做的余割,用“”表示.若该直角三角形的三边分别为a,b,c,则,那么下列说法正确的是( )
A. B. C. D.
10.如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
A. B. C. D.
11.在中,,,,那么下列各式中,正确的是( )
A. B. C. D.
三、解答题
12.如图,某游客在山脚下乘览车上山.导游告知,索道与水平线成角∠BAC为40°,览车速度为60米/分,11分钟到达山顶,请根据以上信息计算山的高度BC.
(精确到1米)(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84)
13.学生到工厂劳动实践,学习机械零件,零件的截面如图所示,已知四边形AEFD为矩形,点B,C分别在EF,DF上,∠ABC为90°,∠BAD=53°,AB=10cm,BC=6cm,求零件的截面面积.
参考数据:sin53°≈0.80,cos53°≈0.60.
14.如图,已知Rt△ABO,∠BAO=90°,以点O为坐标原点,OA所在直线为y轴,建立平面直角坐标系,AO=3,∠AOB=30°,将Rt△ABO沿OB翻折后,点A落在第一象限内的点D处.
(1)求D点坐标;
(2)若抛物线y=ax2+bx+3(a≠0)经过B、D两点,求此抛物线的表达式;
(3)若抛物线的顶点为E,它的对称轴与OB交于点F,点P为射线OB上一动点,过点P作y轴的平行线,交抛物线于点M.是否存在点P,使得以E、F、M、P为顶点的四边形为等腰梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
四、计算题
15.计算:
16.计算:
(1);
(2).
五、综合题
17.在一次数学综合实践活动中,某数学小组的同学们一起测量一座小山的高度.如图,在点A处测得山顶E的仰角为,向山的方向前进,在点C处测得山顶E的仰角为,已知观测点A,C到地面的距离,.求小山的高度(精确到).(参考数据:,,,)
18.某数学实践活动小组安排了一次主题项目学习,请你利用所学知识回答表格中的问题.
实践主题 数学来源于生活,数学服务于生活
实践目标 运用所学知识进行实地测量,深入探究数学知识
工具准备 测角仪、测距仪、作图工具等
测量方案 【实践场地】 学校有一块三角形池塘,两边,紧靠围墙, 为一条笔直小路,无法直接确定池塘的边长,
【实践过程】 ①用测角仪测量围墙与小路所成夹角,; ②用测距仪测量小路的长
【数据收集】 ,,
提出问题 (1)两面围墙的夹角的度数为 ; (2)三角形池塘的面积为多少
深入探讨 (3)如何利用测量数据求出的值
19.如图1是一种手机平板支架,由底座、支撑板和托板构成,手机放置在托板上,如图2是其侧面示意图,量得底座长AB=11cm,支撑板长BC=8cm,托板长CD=6cm,托板CD固定在支撑板顶端点C处,托板CD可绕点C旋转,支撑板BC可绕点B转动。
(1)如果∠ABC=60°,∠BCD=70,求点D到直线AB的距离(精确到0.1cm);
(2)在第(1)小题的条件下,如果把线段CD绕点C顺时针旋转20°后, 再将线段BC绕点B逆时针旋转,使点D落在直线AB上,求线段BC旋转的角度.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.73)
六、实践探究题
20.如图,
定义:在Rt△ABC中,锐角ɑ的邻边与对边的比叫做∠ɑ的余切,记做cotɑ,即.根据上述角的余切定义,解答下列问题:
(1)cot45°= .
(2)已知,其中∠A为锐角,则cotA的值为 .
答案解析部分
1.【答案】
【知识点】解直角三角形
2.【答案】
【知识点】求特殊角的三角函数值
3.【答案】2
【知识点】锐角三角函数的定义
4.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】3
【知识点】解直角三角形
6.【答案】 , , ,
【知识点】一次函数中的动态几何问题
7.【答案】D
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】锐角三角函数的定义
11.【答案】C
【知识点】锐角三角函数的定义
12.【答案】解:由题意可得:∠BAC=40°,AB=66米.
∵sin40°= ,∴BC≈0.64×660=422.4米≈422米.
答:山的高度BC约为422米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】解:∵∠BAD=53°;
∴∠EAB=37°;
∴∠EBA=53°;
∴AE=ABxsin∠EBA=10x0.8=8cm;
∴BE= cm;
∵∠ABC=90°;
∴∠CBF=37°;
∴∠BCF=53°;
∴BF=BCxsin∠BCF=6x0.8=4.8cm;
∴CF= 3.6cm;
=8x10.8- x8x6- x4.8x3.6
=53.76cm2
【知识点】矩形的性质;求特殊角的三角函数值
14.【答案】解:(1)过点D作DE⊥x轴于点E,如图(1).由翻折可知:DO=AO=3,∠AOB=∠BOD=30°,∴∠DOE=30°.∴DE=在Rt△COD中,由勾股定理,得OE=∴D(,)(2)在Rt△AOB中,AB=AO tan30°=3×=,∴B(,3).∵抛物线y=ax2+bx+3(a≠0)经过B(,3),D(,)两点,∴解得∴此抛物线表达式为y=﹣x2+x+3.(3)存在符合条件的点P,设P(x,y),作EH⊥PM于点H,FG⊥PM于点G,如图(2).∵E为抛物线y=﹣x2+x+3的顶点,∴E(,).设OB所在直线的表达式为y=kx,将点B(,3)代入,得k=,∴y=x.∵P在射线OB上,∴P(x,x),F(,).则H(x,)G(x,).∵M在抛物线上,M(x,﹣x2++3).要使四边形EFMP为等腰梯形,只需PH=GM.x﹣=﹣(﹣x2+x+3),即﹣x2+x+3+x=5.解得x1=2,x2=.∴P1点坐标为(2,6),P2点坐标为(,)与F重合,应舍去.∴P点坐标为(2,6).
【知识点】二次函数的实际应用-几何问题
15.【答案】
【知识点】求特殊角的三角函数值
16.【答案】(1)解:原式
=1.
(2)解:原式
.
【知识点】求特殊角的三角函数值
17.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
18.【答案】(1);(2);(3)
【知识点】解直角三角形的其他实际应用
19.【答案】(1)解:如图2,过D作DM⊥AB,交AB于点M,过点C作CN⊥AB于点N,垂足为N,过点D作DQ⊥CN交CB于点Q,垂足为F,
在Rt△CNB中,∠ABC=60°,BC=8cm,
∴CN=CB sin∠ABC=8×≈6.92(cm),
∵∠BCN=90°-60°=30°,又∵∠DCB=70°,
∴∠DCF=70°-30°=40°,
在Rt△DCF中,∠DCF=40°,CD=6cm,∴CF=CD cos40°≈6×0.77=4.62(cm),
∵∠DMN=∠MNF=∠NFD=90°,∴四边形MNFD是矩形,
∴DM=FN=CN-CF=6.92-4.62=2.3(cm),
即点D到直线AB的距离为2.3cm;
(2)解:把线段CD绕点C顺时针旋转20°后,∠C′=70°+20°=90°,如图,
∵BC=8cm,CD=6cm,
∴tan∠B=0.75,
∵tan37°≈0.75,
∴∠C′BD′=37°,
∵∠ABC=60°,
∴∠CBC′=60°-37°=23°,
答:线段BC旋转的角度为23°.
【知识点】解直角三角形
20.【答案】(1)1
(2)
【知识点】锐角三角函数的定义;等腰直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
