【沪科版九上同步练习】 九年级上册期末(全册)复习题二(精华)
文档属性
| 名称 | 【沪科版九上同步练习】 九年级上册期末(全册)复习题二(精华) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版九上同步练习】
九年级上册期末(全册)复习题二(精华)
一、单选题
1.如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )
A. 米 B. 米
C. 米 D. 米
2.抛物线y=x2+2x﹣3与坐标轴的交点个数有( )
A.0个 B.1个 C.2个 D.3个
3.已知反比例函数 图像经过点(2,—3),则下列点中必在此函数图象上的是( )
A.(2, 3) B.(1, 6)
C.(—1, 6) D.(—2,—3)
4.在平面直角坐标系中,已知点在抛物线上,且.设,则t的值可以是( )
A. B. C.1 D.
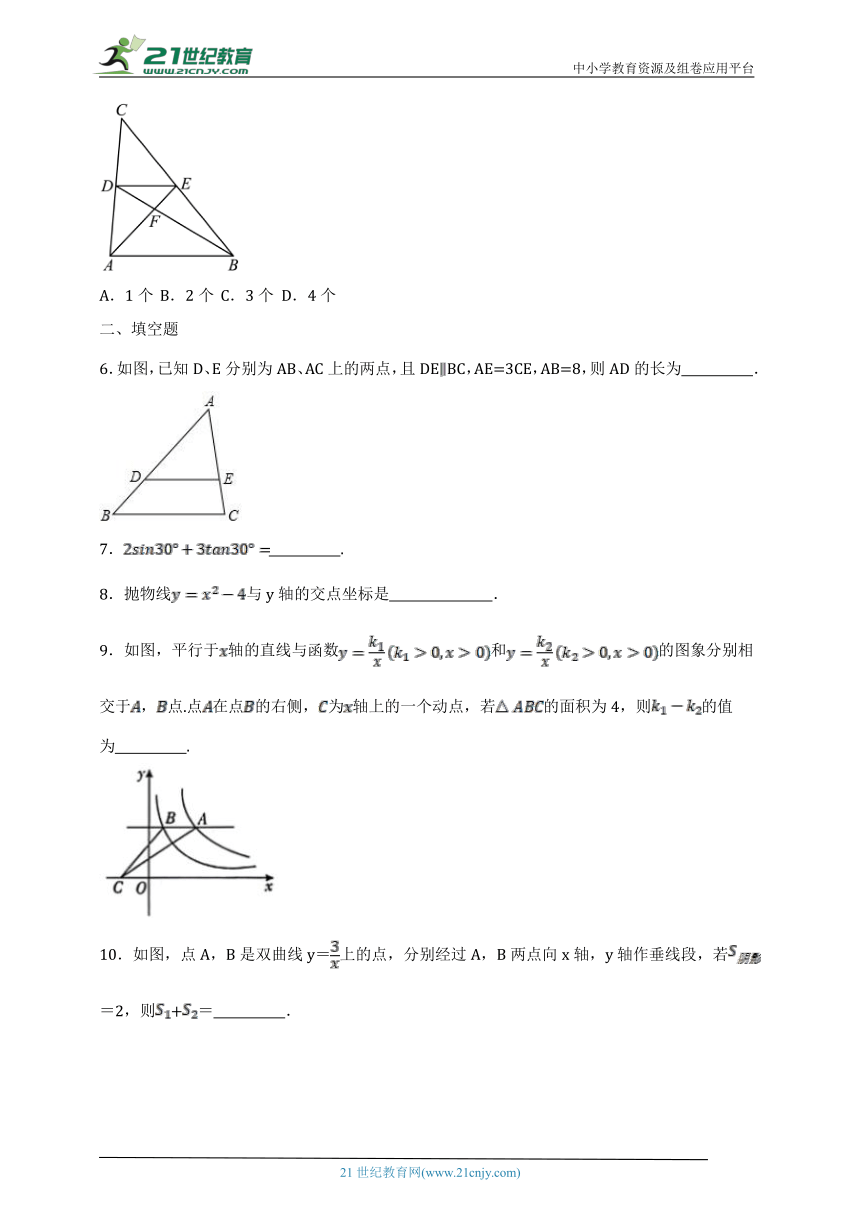
5.如图,在中,中线、相交于点F,连接,则下列结论:①,②,③,④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.如图,已知D、E分别为AB、AC上的两点,且DEBC,AE=3CE,AB=8,则AD的长为 .
7. .
8.抛物线与y轴的交点坐标是 .
9.如图,平行于轴的直线与函数和的图象分别相交于,点.点在点的右侧,为轴上的一个动点,若的面积为4,则的值为 .
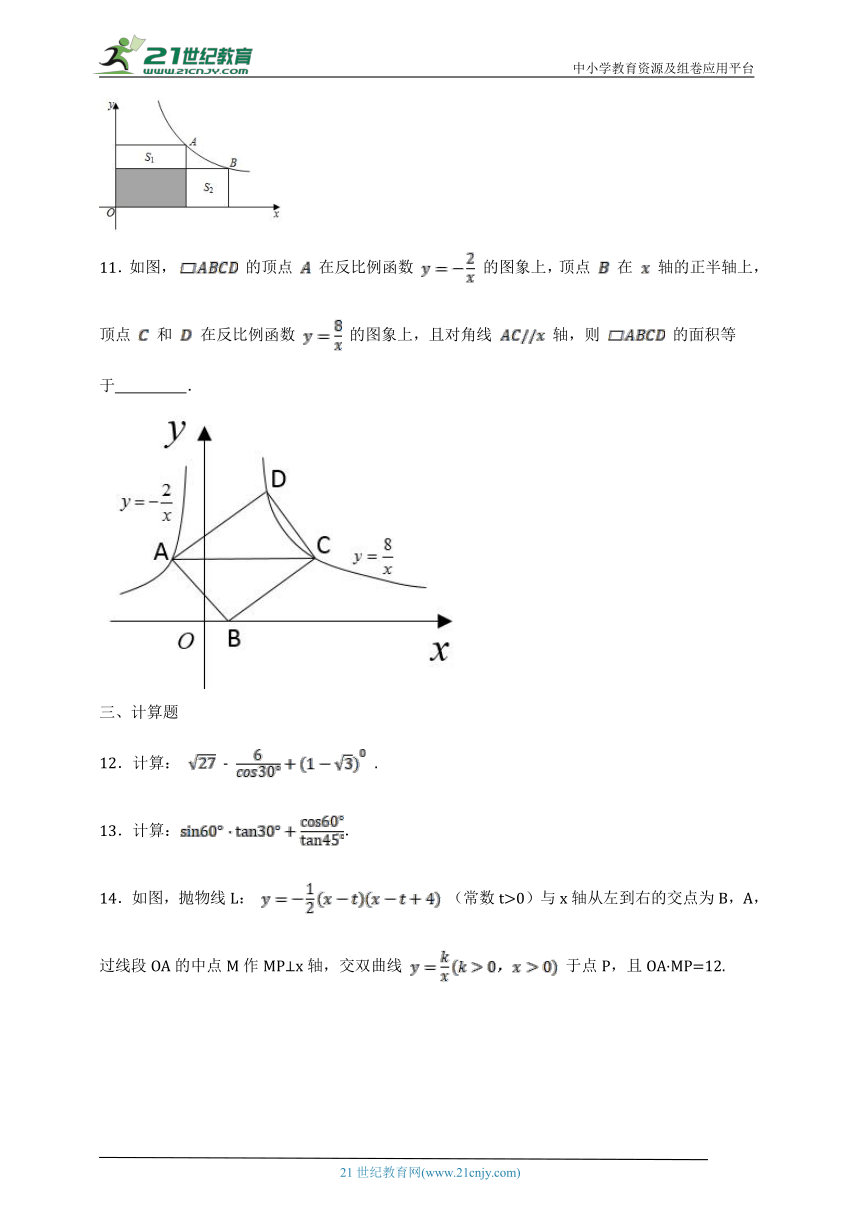
10.如图,点A,B是双曲线y=上的点,分别经过A,B两点向x轴,y轴作垂线段,若=2,则+= .
11.如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 .
三、计算题
12.计算: - .
13.计算:.
14.如图,抛物线L: (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线 于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
四、解答题
15.如图,一次函数和反比例函数的图像交于点,.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出不等式的解集.
16.综合与实践活动中,要利用测角仪测量塔的高度,如图,塔AB前有一座高为DE的观景台,已知CD=6m,∠DCE=30°,点E,C,A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为45°,在观景台D处测得塔顶部B的仰角为27°.
(1)求DE的长.
(2)设塔AB的高度为h.
①用含有h的式子表示线段EA的长(结果保留根号).
②求塔AB的高度(结果精确到1m,参考数据:
17.定义:形如(为用自变量表示的代数式)的函数叫做“翻折函数”.“翻折函数”本质是分段函数.例如,函数,,都是“翻折函数”.可以将“翻折函数”写成分段函数的形式:.
探索并解决下列问题:
(1)将“翻折函数”写成分段函数的形式;
(2)若“翻折函数”函数的图象与直线恰有个公共点,求的取值范围;
(3)已知函数的图象与轴交于点,与轴交于,两点(点在点的左边),点在函数的图象上(点与点不重合),轴,垂足为.若与相似,请直接写出所有符合条件的点的坐标.
五、综合题
18.已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
19.如图,已知矩形 的两条对角线相交于点O,过点 作 分别交 、 于点 、 .
(1)求证: ;
(2)连接 ,若 .求证: .
20.如图,直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(m,8),AB⊥x轴,垂足为B。
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标。
六、实践探究题
21.
(1)【问题探究】如图1,点F是正方形边上一点,射线交对角线于点E,交的延长线于点G.证明;
(2)【知识迁移】如图2,点F是平行四边形边上一点,射线交对角线于点E,交的延长线于点G.证明:
(3)【拓展应用】如图3,是的中线,点E是上一点,过点C作,连接并延长交于点F,交于点G,若,求的值.
答案解析部分
1.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
2.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】C
【知识点】反比例函数图象上点的坐标特征
4.【答案】C
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
5.【答案】D
【知识点】相似三角形的判定与性质;三角形的中位线定理
6.【答案】6
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
7.【答案】
【知识点】求特殊角的三角函数值
8.【答案】(0,-4)
【知识点】二次函数图象与坐标轴的交点问题
9.【答案】8
【知识点】反比例函数系数k的几何意义
10.【答案】2
【知识点】反比例函数系数k的几何意义
11.【答案】10
【知识点】反比例函数系数k的几何意义;平行四边形的判定与性质
12.【答案】解:
= +1
= +1
=
【知识点】实数的运算;求特殊角的三角函数值
13.【答案】解:原式=
=1
【知识点】求特殊角的三角函数值
14.【答案】(1)解:设点P (x, y),则MP=y,由OA的中点为M知O4= 2x,代入OA.MP=12,
得2x.y=12,即xy=6.
∴k= xy=6.
(2)解:当t=1时,令y=0,
∴由B在A左边,得B (-3,0),A (1, 0),∴AB=4.
∵L的对称轴为x=-1,而M为( ,0),
∴MP与L对称轴的距离为 .
(3)解:∵A (t, 0),B (t-4,0),
∴L的对称轴为x=t-2.
又MP为x=
当t-2≤ ,即t≤4时,顶点(t-2,2)就是G的最高点;
当t>4时,L与MP的交点( , )就是G的最高点.
(4)解:5≤t≤8- 或7≤1≤8+
【知识点】反比例函数图象上点的坐标特征;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
15.【答案】(1);
(2)6
(3)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
16.【答案】(1)解:由题意得:DE⊥EC,
在Rt△DEC中,CD=6m,∠DCE=30°,
∴,
∴DE的长为3m.
(2)解:①由题意得:BA⊥EA,
在Rt△DEC中,DE=3m,CD=6m,
∴,
∵∠BCA=45°,
∴AC=AB=h(m),
则;
②过点D作DF⊥AB,垂足为F,如图:
由题意得:,DE=FA=3m,
∵AB=hm,
∴BF=AB-AF=(h-3)m,
在Rt△BDF中,∠BDF=27°,
∴,
即,
解得:,
∴AB=11m,
∴塔AB的高度约为11m.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
17.【答案】(1)
(2)
(3)点,,
【知识点】待定系数法求一次函数解析式;相似三角形的判定与性质
18.【答案】(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
19.【答案】(1)证明:∵四边形ABCD是矩形
∴∠ABE=90°
∴∠ABG+∠EBG=90°
∵
∴∠ABG+∠BAG=90°
∴∠EBG=∠BAG
∴Rt△BEG∽Rt△AEB
∴
∴
(2)证明:由(1)有:
∵BE=CE
∴
∴
∵∠CEG=∠AEC
∴△CEG∽△AEC
∴∠CGE=∠ACE
∵四边形ABCD是矩形
∴AC=BD
∴OB=OC
∴∠DBC=∠ACE
∴
【知识点】矩形的性质;相似三角形的判定与性质
20.【答案】(1)解:∵直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(m,8),
则2m=8,解得m=4,
∴A(4,8),
∴k=4X8=32;
(2)解:设AC=x,则OC=x,BC=8-x,
在Rt△OBC中,由勾股定理得:OC2=OB2+BC2,
即x2=42+(8-x)2,解得x=5,∴AC=5;
(3)解:设点D的坐标为(x,0),分两种情况:
①当x>4时,如解图①,∵S△OCD= S△ACD
∴ OD·BC= AC·BD,
∴3x=5(x-4),解得x=10;
②当0∴点D的坐标为(10,0)或( ,0)
【知识点】一次函数的图象;反比例函数的图象;反比例函数的性质;一次函数的性质
21.【答案】(1)证明:∵正方形,
∴,
∴,
∴,
∴,
∴;
(2)证明:∵平行四边形,
∴,
∴,
∴,
∴,
∴;
(3)解:延长至点,使,连接,
∵为三角形的中线,
∴,
∴四边形为平行四边形,
∴,
∵,
∴三点共线,
同法(2)可得:,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【知识点】平行四边形的判定与性质;正方形的性质;相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【沪科版九上同步练习】
九年级上册期末(全册)复习题二(精华)
一、单选题
1.如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )
A. 米 B. 米
C. 米 D. 米
2.抛物线y=x2+2x﹣3与坐标轴的交点个数有( )
A.0个 B.1个 C.2个 D.3个
3.已知反比例函数 图像经过点(2,—3),则下列点中必在此函数图象上的是( )
A.(2, 3) B.(1, 6)
C.(—1, 6) D.(—2,—3)
4.在平面直角坐标系中,已知点在抛物线上,且.设,则t的值可以是( )
A. B. C.1 D.
5.如图,在中,中线、相交于点F,连接,则下列结论:①,②,③,④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.如图,已知D、E分别为AB、AC上的两点,且DEBC,AE=3CE,AB=8,则AD的长为 .
7. .
8.抛物线与y轴的交点坐标是 .
9.如图,平行于轴的直线与函数和的图象分别相交于,点.点在点的右侧,为轴上的一个动点,若的面积为4,则的值为 .
10.如图,点A,B是双曲线y=上的点,分别经过A,B两点向x轴,y轴作垂线段,若=2,则+= .
11.如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 .
三、计算题
12.计算: - .
13.计算:.
14.如图,抛物线L: (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线 于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
四、解答题
15.如图,一次函数和反比例函数的图像交于点,.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出不等式的解集.
16.综合与实践活动中,要利用测角仪测量塔的高度,如图,塔AB前有一座高为DE的观景台,已知CD=6m,∠DCE=30°,点E,C,A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为45°,在观景台D处测得塔顶部B的仰角为27°.
(1)求DE的长.
(2)设塔AB的高度为h.
①用含有h的式子表示线段EA的长(结果保留根号).
②求塔AB的高度(结果精确到1m,参考数据:
17.定义:形如(为用自变量表示的代数式)的函数叫做“翻折函数”.“翻折函数”本质是分段函数.例如,函数,,都是“翻折函数”.可以将“翻折函数”写成分段函数的形式:.
探索并解决下列问题:
(1)将“翻折函数”写成分段函数的形式;
(2)若“翻折函数”函数的图象与直线恰有个公共点,求的取值范围;
(3)已知函数的图象与轴交于点,与轴交于,两点(点在点的左边),点在函数的图象上(点与点不重合),轴,垂足为.若与相似,请直接写出所有符合条件的点的坐标.
五、综合题
18.已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
19.如图,已知矩形 的两条对角线相交于点O,过点 作 分别交 、 于点 、 .
(1)求证: ;
(2)连接 ,若 .求证: .
20.如图,直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(m,8),AB⊥x轴,垂足为B。
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标。
六、实践探究题
21.
(1)【问题探究】如图1,点F是正方形边上一点,射线交对角线于点E,交的延长线于点G.证明;
(2)【知识迁移】如图2,点F是平行四边形边上一点,射线交对角线于点E,交的延长线于点G.证明:
(3)【拓展应用】如图3,是的中线,点E是上一点,过点C作,连接并延长交于点F,交于点G,若,求的值.
答案解析部分
1.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
2.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】C
【知识点】反比例函数图象上点的坐标特征
4.【答案】C
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
5.【答案】D
【知识点】相似三角形的判定与性质;三角形的中位线定理
6.【答案】6
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
7.【答案】
【知识点】求特殊角的三角函数值
8.【答案】(0,-4)
【知识点】二次函数图象与坐标轴的交点问题
9.【答案】8
【知识点】反比例函数系数k的几何意义
10.【答案】2
【知识点】反比例函数系数k的几何意义
11.【答案】10
【知识点】反比例函数系数k的几何意义;平行四边形的判定与性质
12.【答案】解:
= +1
= +1
=
【知识点】实数的运算;求特殊角的三角函数值
13.【答案】解:原式=
=1
【知识点】求特殊角的三角函数值
14.【答案】(1)解:设点P (x, y),则MP=y,由OA的中点为M知O4= 2x,代入OA.MP=12,
得2x.y=12,即xy=6.
∴k= xy=6.
(2)解:当t=1时,令y=0,
∴由B在A左边,得B (-3,0),A (1, 0),∴AB=4.
∵L的对称轴为x=-1,而M为( ,0),
∴MP与L对称轴的距离为 .
(3)解:∵A (t, 0),B (t-4,0),
∴L的对称轴为x=t-2.
又MP为x=
当t-2≤ ,即t≤4时,顶点(t-2,2)就是G的最高点;
当t>4时,L与MP的交点( , )就是G的最高点.
(4)解:5≤t≤8- 或7≤1≤8+
【知识点】反比例函数图象上点的坐标特征;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
15.【答案】(1);
(2)6
(3)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
16.【答案】(1)解:由题意得:DE⊥EC,
在Rt△DEC中,CD=6m,∠DCE=30°,
∴,
∴DE的长为3m.
(2)解:①由题意得:BA⊥EA,
在Rt△DEC中,DE=3m,CD=6m,
∴,
∵∠BCA=45°,
∴AC=AB=h(m),
则;
②过点D作DF⊥AB,垂足为F,如图:
由题意得:,DE=FA=3m,
∵AB=hm,
∴BF=AB-AF=(h-3)m,
在Rt△BDF中,∠BDF=27°,
∴,
即,
解得:,
∴AB=11m,
∴塔AB的高度约为11m.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
17.【答案】(1)
(2)
(3)点,,
【知识点】待定系数法求一次函数解析式;相似三角形的判定与性质
18.【答案】(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
19.【答案】(1)证明:∵四边形ABCD是矩形
∴∠ABE=90°
∴∠ABG+∠EBG=90°
∵
∴∠ABG+∠BAG=90°
∴∠EBG=∠BAG
∴Rt△BEG∽Rt△AEB
∴
∴
(2)证明:由(1)有:
∵BE=CE
∴
∴
∵∠CEG=∠AEC
∴△CEG∽△AEC
∴∠CGE=∠ACE
∵四边形ABCD是矩形
∴AC=BD
∴OB=OC
∴∠DBC=∠ACE
∴
【知识点】矩形的性质;相似三角形的判定与性质
20.【答案】(1)解:∵直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(m,8),
则2m=8,解得m=4,
∴A(4,8),
∴k=4X8=32;
(2)解:设AC=x,则OC=x,BC=8-x,
在Rt△OBC中,由勾股定理得:OC2=OB2+BC2,
即x2=42+(8-x)2,解得x=5,∴AC=5;
(3)解:设点D的坐标为(x,0),分两种情况:
①当x>4时,如解图①,∵S△OCD= S△ACD
∴ OD·BC= AC·BD,
∴3x=5(x-4),解得x=10;
②当0
【知识点】一次函数的图象;反比例函数的图象;反比例函数的性质;一次函数的性质
21.【答案】(1)证明:∵正方形,
∴,
∴,
∴,
∴,
∴;
(2)证明:∵平行四边形,
∴,
∴,
∴,
∴,
∴;
(3)解:延长至点,使,连接,
∵为三角形的中线,
∴,
∴四边形为平行四边形,
∴,
∵,
∴三点共线,
同法(2)可得:,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【知识点】平行四边形的判定与性质;正方形的性质;相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
