第二十八章锐角三角函数 单元复习题 (含解析)人教版九年级数学下册
文档属性
| 名称 | 第二十八章锐角三角函数 单元复习题 (含解析)人教版九年级数学下册 | 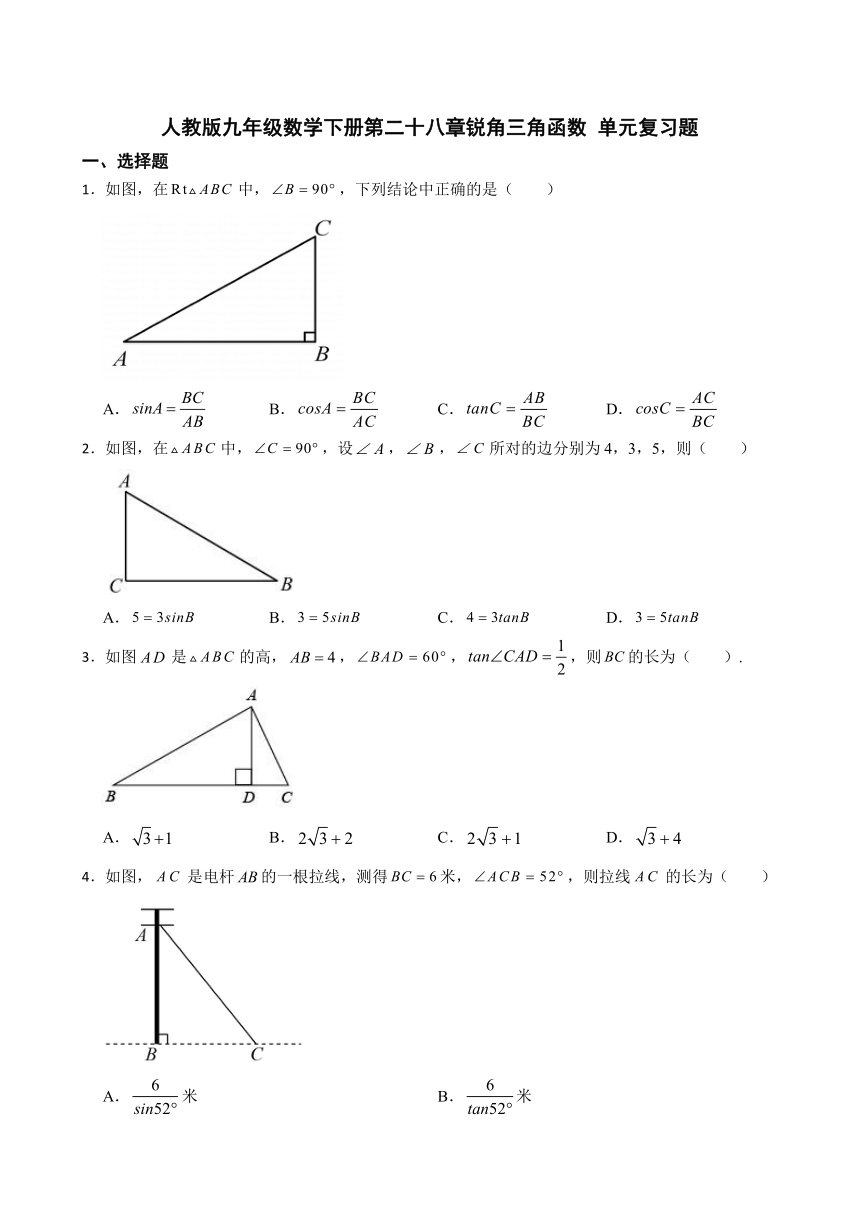 | |
| 格式 | docx | ||
| 文件大小 | 621.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 17:18:51 | ||
图片预览




文档简介
人教版九年级数学下册第二十八章锐角三角函数 单元复习题
一、选择题
1.如图,在中,,下列结论中正确的是( )
A. B. C. D.
2.如图,在中,,设,,所对的边分别为4,3,5,则( )
A. B. C. D.
3.如图是的高,,,,则的长为( ).
A. B. C. D.
4.如图,是电杆的一根拉线,测得米,,则拉线的长为( )
A.米 B.米
C.米 D.米
5.如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数,在第一象限内的图像交于点B,连接,若,,则m的值是( )
A.6 B.8 C.10 D.12
6.在中,,、、所对的边分别是a、b、c.则下列各式中,正确的是( )
A. B. C. D.
7.如图,在中,是边上的点,以为圆心,为半径的与相切于点,平分,,,的长是( )
A. B.2 C. D.
8. 如图,某校教学楼与的水平间距,在教学楼的顶部点测得教学楼的顶部点的仰角为,测得教学楼的底部点的俯角为,则教学楼的高度是( )
A. B.
C. D.
二、填空题
9.若,则锐角 .
10.小明沿坡比为1︰ 的山坡向上走了100米.那么他升高了 米.
11.在△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,tan∠BPC= .
12.如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB= m(结果精确到1m).
三、计算题
13.计算:
14.计算:.
四、解答题
15.先化简,再求值:,其中.
16.如图,建筑物AB垂直于地面,测角机器人先在C处测得A的仰角为,再向着B前进6米到D处,测得A的仰角为.求建筑物AB的高度(结果精确到米).(参考数据:,,)
五、综合题
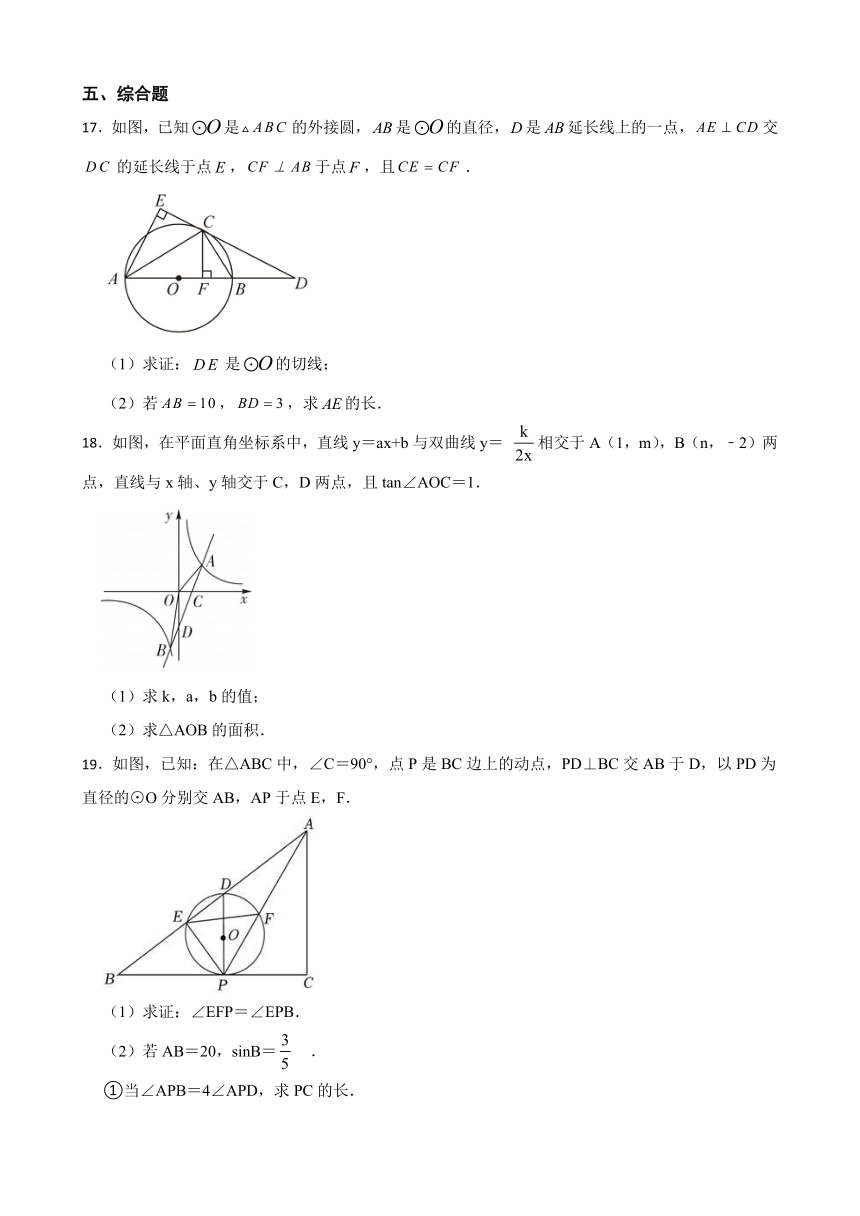
17.如图,已知是的外接圆,是的直径,是延长线上的一点,交的延长线于点,于点,且.
(1)求证:是的切线;
(2)若,,求的长.
18.如图,在平面直角坐标系中,直线y=ax+b与双曲线y= 相交于A(1,m),B(n,﹣2)两点,直线与x轴、y轴交于C,D两点,且tan∠AOC=1.
(1)求k,a,b的值;
(2)求△AOB的面积.
19.如图,已知:在△ABC中,∠C=90°,点P是BC边上的动点,PD⊥BC交AB于D,以PD为直径的⊙O分别交AB,AP于点E,F.
(1)求证:∠EFP=∠EPB.
(2)若AB=20,sinB= .
①当∠APB=4∠APD,求PC的长.
②当△PEF为等腰三角形时,请求出所有满足条件的△PEF的腰长.
(3)若sinB=,且D,F,C在一条直线上,则DP与AC的比值为 .
答案解析部分
1.【答案】C
【解析】【解答】解:在Rt△ABC中,∠B=90°,
则.
故答案为:C.
【分析】在直角三角形中,根据锐角三角函数“、、”并结合题意可判断求解.
2.【答案】B
【解析】【解答】解:在△ABC中,∠C=90°,设∠A、∠B,∠C所对的边分别为4,3,5,
所以sinB=,即3=5sinB,因此选项A不符合题意,选项B符合题意,
tanB=,即3=4tanB,因此选项C不符合题意,选项D不符合题意,
故答案为:B.
【分析】A、根据锐角三角函数可得3=5sinB;
B、根据锐角三角函数可得3=5sinB;
C、根据锐角三角函数可得3=4tanB;
D、根据锐角三角函数可得3=4tanB.
3.【答案】C
【解析】【解答】解:∵AD是△ABC的高,∠BAD=60°,
∴,
∴,
∴.
∵,即,
∴,
解得:,
∴.
故答案为:C.
【分析】根据直角三角形的两锐角互余得∠ABD=30°,根据含30°角直角三角形的性质得AD=2,再由勾股定理算出BD的长,进而根据正切函数的定义可求出CD的长,最后根据BC=BD+CD即可求出答案.
4.【答案】D
【解析】【解答】解: ,
,
米,
米;
故答案为:D.
【分析】利用解直角三角形的方法可得 。
5.【答案】D
【解析】【解答】解:过点B作BD⊥y轴于点D,
令y=kx+4中的x=0,得y=4,
∴C(0,4),
∴OC=4.
∵S△OBC=4,
∴OC·BD=4,
∴BD=2.
∵tan∠BOC=,
∴OD=6,
∴B(2,6).
∵点B在反比例函数y=的图象上,
∴m=2×6=12.
故答案为:D.
【分析】过点B作BD⊥y轴于点D,易得C(0,4),则OC=4,根据三角形的面积公式可得BD的值,利用三角函数的概念可得OD,据此可得点B的坐标,然后代入y=中就可求出m的值.
6.【答案】C
【解析】【解答】解:在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴sinA=.
故答案为:C.
【分析】直接根据三角函数的概念进行判断.
7.【答案】A
【解析】【解答】解:∵AC是圆O的切线,
∴OD⊥AC,
∴∠ADO=90°,
∵,
∴∠A=30°,
∴∠AOD=90°-30°=60°;
∵OD=OB,
∴∠OBD=∠ODB,
∵∠AOD=∠OBD+∠ODB=60°,
解之:∠OBD=30°,
∵BD平分∠ABC,
∴∠ABC=2∠OBD=2×30°=60°,
∴∠C=180°-∠A-∠ABC=180°-30°-60°=90°,
在Rt△ABC中
即,
解之:,
设OD=x,则AO=12-x,
∴12-x=2x,
解之:x=4,
∴OD=4
∴,
∴.
故答案为:A
【分析】利用切线的性质可证得∠ADO=90°,利用锐角三角函数的定义和特殊角的三角函数值,可求出∠A=30°,∠AOD=60°,利用三角形的外角的性质和角平分线的定义求出∠ABC的度数,可证得∠C=90°;再利用解直角三角形求出AC的长,利用30°角所对的直角边等于斜边的一半,可求出OD的长,即可得到AD的长.
8.【答案】A
【解析】【解答】解:过点作,垂足为,
由题意得:
米,
在中,,
米,
在中,,
米,
米,
故答案为:A.
【分析】过点C作CE⊥AB,垂足为E,由题意可得CE=BD=a米,根据三角函数的概念可得BE、AE,然后根据AB=AE+BE进行计算.
9.【答案】60°
【解析】【解答】解:∵,
∴,
故答案为.
【分析】根据cos60°=即可求解.
10.【答案】50
【解析】【解答】解:如图所示,
∵坡比为1︰ ,
∴
∴ (由勾股定理可得)
∵AB=100m,
∴AC= m
故答案为:50.
【分析】根据题意画出图形,根据坡度的定义可以求得AC、BC的比值,由勾股定理可得AC、AB的比值,再由AB=100m,即可得出AC的长.
11.【答案】
【解析】【解答】解:过点A作AD⊥BC于点D,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
∵AB=AC=5,BC=8,
∴BD=CD=4,
∴AD==3.
∵∠BAD=∠CAD, ∠BPC=∠BAC
∴∠BPC=∠BAD,
∴tan∠BPC=tan∠BAD=.
故答案为:.
【分析】过点A作AD⊥BC于点D,由等腰三角形的性质可得∠BAD=∠CAD,BD=CD=4,利用勾股定理可得AD,结合∠BPC=∠BAC可得∠BPC=∠BAD,然后利用三角函数的概念进行计算.
12.【答案】24
【解析】【解答】解:在Rt△ABC中,∠BCA=60°,
,
∴.
故答案为:24
【分析】在Rt△ABC中,利用解直角三角形求出AB的长.
13.【答案】解;原式
.
【解析】【分析】先代入特殊锐角三角函数值,再根据0指数幂的性质、负整数指数幂的性质分别化简,最后计算有理数的加减法可得答案.
14.【答案】解:
.
【解析】【分析】根据负整数指数幂的运算性质、特殊角的三角函数值可得原式=-2+-4×,然后计算乘法,再根据二次根式的减法法则进行计算.
15.【答案】解:
=
=
=.
∵=2×+1=+1,
∴原式===.
【解析】【分析】对括号中的第二个分式的分母进行分解,然后对括号中的式子进行通分,将除法化为乘法,再进行约分即可对原式进行化简,根据特殊角的三角函数值可得a的值,然后代入化简后的式子中进行计算.
16.【答案】解:由题意可得:,,,,
∴,,
∴,,
∴,
解得:,即建筑物AB的高度为14米.
【解析】【分析】由∠C及∠ADB的正切函数可得 ,, 进而根据CD=BC-BD建立方程,求解可得AB的长.
17.【答案】(1)证明:如图,连接
由题意知,,
在和值
∵
∴
∴
∵
∴
∵
∴
∴
又∵是半径
∴是的切线.
(2)解:∵
∴
∴
∵
∴
又∵
∴
∴即
解得
∵,
∵
∴
在中,
【解析】【分析】(1)连接OC,由圆周角定理可得∠ACB=90°,由垂直的概念可得∠AEC=∠AFC=90°,利用HL证明△AEC≌△AFC,得到∠EAC=∠FAC,由等腰三角形的性质可得∠ACO=∠FAC,结合∠EAC+∠ECA=90°可得OC⊥AE,据此证明;
(2)由同角的余角相等可得∠ACO=∠BCD,由等腰三角形的性质可得∠CAD=∠ACO,则∠CAD=∠BCD,由两角对应相等的两个三角形相似可得△BCD∽△CAD,利用相似三角形的性质求出CD的值,由OD=OB+BD可得OD,利用三角函数的概念可得DE,然后由勾股定理就可求出AE.
18.【答案】(1)解:过点A作AE⊥x轴于点E,如图
∵tan∠AOC=1,A(1,m),B(n,﹣2)
∴m=1
∴1=
∴k=2
∴﹣2=
∴n=﹣
∴A(1,1),B(﹣,﹣2)
把A(1,1),B(﹣,﹣2)分别代入y=ax+b得:
解得
∴y=2x﹣1
∴k,a,b的值分别为2,2,﹣1.
(2)解:∵y=2x﹣1
∴当x=0时,y=﹣1,即D(0,﹣1)
∴S△AOB=OD×xA+OD×(﹣xB)
=OD×(xA﹣xB)
=×1×(1+)
=
∴△AOB的面积为.
【解析】【分析】(1)过点A作AE⊥x轴于点E,tan∠AOC=1,利用点A的坐标,可求出m的值,代入函数解析式,可求出k的值,即可得到函数解析式,从而可求出n的值,可得到点B的坐标,然后将点A,B的坐标分别代入一次函数解析式,可得到关于a,b的方程组,解方程组求出a,b的值,即可得到一次函数解析式.
(2)利用一次函数解析式求出点D的坐标,再利用三角形的面积公式求出△AOB的面积.
19.【答案】(1)证明:∵PD为⊙O的直径,PD⊥BC,
∴BC为⊙O的切线,
∴∠EFP=∠EPB
(2)解:①∵∠APB=4∠APD,∠APB=90°+∠APD,
∴4∠APD=90°+∠APD,
∴∠APD=30°.
∴∠APC=90°﹣∠APD=60°.
∵AB=20,sinB=,
∴AC=AB sinB=20×=12.
∵tan∠APC==,
∴PC= =4;
②当EF=EP时,
∵EF=EP,
∴∠EPF=∠EFP,
∵∠EFP=∠EPB,
∴∠EPF=∠EPB.
∵PD为⊙O的直径,
∴PE⊥AB.
∴∠BEP=∠AEP=90°,
在△BEP和△AEP中,
∴△BEP≌△AEP(ASA),
∴BE=AE=10.
∵sinB=,
∴tanB==,
∴PE=;
当EP=FP时,
∵EP=FP,
∴,
∵PD为⊙O的直径,
∴PD⊥EF,
∵PD⊥BC,
∴EF∥BC.
∴∠B=∠AEF,
∵∠AEF=∠DPF,
∴∠B=∠DPF.
∵PD⊥EF,AC⊥BC,
∴DP∥AC,
∴∠DPF=∠PAC,
∴∠PAC=∠B.
∴tan∠PAC=tanB==.
∴PC=9.
∴PB=BC﹣PC=7.
∵sinB==
∴PE=;
当FE=PF时,
∵FE=PF,
∴∠FEP=∠FPE.
∵FEP+∠AEF=90°,∠FPE+∠FAE=90°,
∴∠AEF=∠FAE,
∴EF=AF.
∴AF=FP=EF.
∵∠DPA=∠AEF,
∴∠DPA=∠DAP,
∴PD=AD.
设PD=AD=3x,
∵sinB==,
∴BD=5x.
∴AB=BD+AD=8x=20,
∴X=.
∴BD=5x=.
∵cosB=,
∴BP=10.
∴PC=BC﹣BP=6.
∴AP= = 6.
∴PF=AP=3.
综上,当△PEF为等腰三角形时,满足条件的△PEF的腰长为3或或.
(3)
【解析】【解答】解:(3)当D,F,C在一条直线上时,
∵PD为⊙O的直径,
∴PF⊥CD,
∴∠FAC+∠FCA=90°,
∵∠FCP+∠FCA=90°,
∴∠FAC=∠FCP.
∵∠ACP=∠DPC=90°,
∴△ACP∽△CPD.
∴
∴PC2=AC PD.
∵sinB= ,
∴∠B=45°.
∴BC=AC,PD=PB.
∴PC=BC﹣BP=AC﹣PD.
∴(AC﹣PD)2=AC PD,
∴DP2﹣3DP AC+AC2=0.
解得:DP= AC或DP=AC(不合题意,舍去).
∴= ,
故答案为:
【分析】(1)利用PD为⊙O的直径,PD⊥BC,可证得CB是圆O的切线,再利用弦切角定理可证得结论.
(2)①利用已知可得到4∠APD=90°+∠APD,可求出∠APD=30°,从而可求出∠APC的度数,利用解直角三角形求出AB、AC、PC的长;②利用△PEF是等腰三角形,分情况讨论:当EF=EP时,由EF=EP,可推出∠EPF=∠EFP,由此可证得∠EPF=∠EPB,利用圆周角定理求出∠BEP=∠AEP=90°,利用ASA证明△BEP≌△AEP,利用全等三角形的性质可求出AE的长;再利用解直角三角形求出PE的长;当EP=FP时,由EP=PF,可证得,利用垂径定理可证得PD⊥EF,由此可推出EF∥BC,利用平行线的性质可证得∠B=∠AEF=∠DPF;再证明DP∥AC,可得到∠DPF=∠PAC=∠B,利用解直角三角形求出PC的长,根据PB=BC-PC,代入计算求出PB的长,利用解直角三角形求出PE的长;当FE=PF时,利用等边对等角可证得∠FEP=∠FPE,利用余角的性质可证得∠AEF=∠FAE,利用等角对等边可得到EF=AF=FP,从而可推出PD=AD=2x,利用解直角三角形表示出BD的长,根据AB=BD+AD,据此可得到关于x的方程,解方程求出x的值可求出BD,BP的长,继而可求出PC的长,利用勾股定理求出AP的长,然后求出PF的长;综上所述可得到符合题意的PF的长.
一、选择题
1.如图,在中,,下列结论中正确的是( )
A. B. C. D.
2.如图,在中,,设,,所对的边分别为4,3,5,则( )
A. B. C. D.
3.如图是的高,,,,则的长为( ).
A. B. C. D.
4.如图,是电杆的一根拉线,测得米,,则拉线的长为( )
A.米 B.米
C.米 D.米
5.如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数,在第一象限内的图像交于点B,连接,若,,则m的值是( )
A.6 B.8 C.10 D.12
6.在中,,、、所对的边分别是a、b、c.则下列各式中,正确的是( )
A. B. C. D.
7.如图,在中,是边上的点,以为圆心,为半径的与相切于点,平分,,,的长是( )
A. B.2 C. D.
8. 如图,某校教学楼与的水平间距,在教学楼的顶部点测得教学楼的顶部点的仰角为,测得教学楼的底部点的俯角为,则教学楼的高度是( )
A. B.
C. D.
二、填空题
9.若,则锐角 .
10.小明沿坡比为1︰ 的山坡向上走了100米.那么他升高了 米.
11.在△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,tan∠BPC= .
12.如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB= m(结果精确到1m).
三、计算题
13.计算:
14.计算:.
四、解答题
15.先化简,再求值:,其中.
16.如图,建筑物AB垂直于地面,测角机器人先在C处测得A的仰角为,再向着B前进6米到D处,测得A的仰角为.求建筑物AB的高度(结果精确到米).(参考数据:,,)
五、综合题
17.如图,已知是的外接圆,是的直径,是延长线上的一点,交的延长线于点,于点,且.
(1)求证:是的切线;
(2)若,,求的长.
18.如图,在平面直角坐标系中,直线y=ax+b与双曲线y= 相交于A(1,m),B(n,﹣2)两点,直线与x轴、y轴交于C,D两点,且tan∠AOC=1.
(1)求k,a,b的值;
(2)求△AOB的面积.
19.如图,已知:在△ABC中,∠C=90°,点P是BC边上的动点,PD⊥BC交AB于D,以PD为直径的⊙O分别交AB,AP于点E,F.
(1)求证:∠EFP=∠EPB.
(2)若AB=20,sinB= .
①当∠APB=4∠APD,求PC的长.
②当△PEF为等腰三角形时,请求出所有满足条件的△PEF的腰长.
(3)若sinB=,且D,F,C在一条直线上,则DP与AC的比值为 .
答案解析部分
1.【答案】C
【解析】【解答】解:在Rt△ABC中,∠B=90°,
则.
故答案为:C.
【分析】在直角三角形中,根据锐角三角函数“、、”并结合题意可判断求解.
2.【答案】B
【解析】【解答】解:在△ABC中,∠C=90°,设∠A、∠B,∠C所对的边分别为4,3,5,
所以sinB=,即3=5sinB,因此选项A不符合题意,选项B符合题意,
tanB=,即3=4tanB,因此选项C不符合题意,选项D不符合题意,
故答案为:B.
【分析】A、根据锐角三角函数可得3=5sinB;
B、根据锐角三角函数可得3=5sinB;
C、根据锐角三角函数可得3=4tanB;
D、根据锐角三角函数可得3=4tanB.
3.【答案】C
【解析】【解答】解:∵AD是△ABC的高,∠BAD=60°,
∴,
∴,
∴.
∵,即,
∴,
解得:,
∴.
故答案为:C.
【分析】根据直角三角形的两锐角互余得∠ABD=30°,根据含30°角直角三角形的性质得AD=2,再由勾股定理算出BD的长,进而根据正切函数的定义可求出CD的长,最后根据BC=BD+CD即可求出答案.
4.【答案】D
【解析】【解答】解: ,
,
米,
米;
故答案为:D.
【分析】利用解直角三角形的方法可得 。
5.【答案】D
【解析】【解答】解:过点B作BD⊥y轴于点D,
令y=kx+4中的x=0,得y=4,
∴C(0,4),
∴OC=4.
∵S△OBC=4,
∴OC·BD=4,
∴BD=2.
∵tan∠BOC=,
∴OD=6,
∴B(2,6).
∵点B在反比例函数y=的图象上,
∴m=2×6=12.
故答案为:D.
【分析】过点B作BD⊥y轴于点D,易得C(0,4),则OC=4,根据三角形的面积公式可得BD的值,利用三角函数的概念可得OD,据此可得点B的坐标,然后代入y=中就可求出m的值.
6.【答案】C
【解析】【解答】解:在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴sinA=.
故答案为:C.
【分析】直接根据三角函数的概念进行判断.
7.【答案】A
【解析】【解答】解:∵AC是圆O的切线,
∴OD⊥AC,
∴∠ADO=90°,
∵,
∴∠A=30°,
∴∠AOD=90°-30°=60°;
∵OD=OB,
∴∠OBD=∠ODB,
∵∠AOD=∠OBD+∠ODB=60°,
解之:∠OBD=30°,
∵BD平分∠ABC,
∴∠ABC=2∠OBD=2×30°=60°,
∴∠C=180°-∠A-∠ABC=180°-30°-60°=90°,
在Rt△ABC中
即,
解之:,
设OD=x,则AO=12-x,
∴12-x=2x,
解之:x=4,
∴OD=4
∴,
∴.
故答案为:A
【分析】利用切线的性质可证得∠ADO=90°,利用锐角三角函数的定义和特殊角的三角函数值,可求出∠A=30°,∠AOD=60°,利用三角形的外角的性质和角平分线的定义求出∠ABC的度数,可证得∠C=90°;再利用解直角三角形求出AC的长,利用30°角所对的直角边等于斜边的一半,可求出OD的长,即可得到AD的长.
8.【答案】A
【解析】【解答】解:过点作,垂足为,
由题意得:
米,
在中,,
米,
在中,,
米,
米,
故答案为:A.
【分析】过点C作CE⊥AB,垂足为E,由题意可得CE=BD=a米,根据三角函数的概念可得BE、AE,然后根据AB=AE+BE进行计算.
9.【答案】60°
【解析】【解答】解:∵,
∴,
故答案为.
【分析】根据cos60°=即可求解.
10.【答案】50
【解析】【解答】解:如图所示,
∵坡比为1︰ ,
∴
∴ (由勾股定理可得)
∵AB=100m,
∴AC= m
故答案为:50.
【分析】根据题意画出图形,根据坡度的定义可以求得AC、BC的比值,由勾股定理可得AC、AB的比值,再由AB=100m,即可得出AC的长.
11.【答案】
【解析】【解答】解:过点A作AD⊥BC于点D,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
∵AB=AC=5,BC=8,
∴BD=CD=4,
∴AD==3.
∵∠BAD=∠CAD, ∠BPC=∠BAC
∴∠BPC=∠BAD,
∴tan∠BPC=tan∠BAD=.
故答案为:.
【分析】过点A作AD⊥BC于点D,由等腰三角形的性质可得∠BAD=∠CAD,BD=CD=4,利用勾股定理可得AD,结合∠BPC=∠BAC可得∠BPC=∠BAD,然后利用三角函数的概念进行计算.
12.【答案】24
【解析】【解答】解:在Rt△ABC中,∠BCA=60°,
,
∴.
故答案为:24
【分析】在Rt△ABC中,利用解直角三角形求出AB的长.
13.【答案】解;原式
.
【解析】【分析】先代入特殊锐角三角函数值,再根据0指数幂的性质、负整数指数幂的性质分别化简,最后计算有理数的加减法可得答案.
14.【答案】解:
.
【解析】【分析】根据负整数指数幂的运算性质、特殊角的三角函数值可得原式=-2+-4×,然后计算乘法,再根据二次根式的减法法则进行计算.
15.【答案】解:
=
=
=.
∵=2×+1=+1,
∴原式===.
【解析】【分析】对括号中的第二个分式的分母进行分解,然后对括号中的式子进行通分,将除法化为乘法,再进行约分即可对原式进行化简,根据特殊角的三角函数值可得a的值,然后代入化简后的式子中进行计算.
16.【答案】解:由题意可得:,,,,
∴,,
∴,,
∴,
解得:,即建筑物AB的高度为14米.
【解析】【分析】由∠C及∠ADB的正切函数可得 ,, 进而根据CD=BC-BD建立方程,求解可得AB的长.
17.【答案】(1)证明:如图,连接
由题意知,,
在和值
∵
∴
∴
∵
∴
∵
∴
∴
又∵是半径
∴是的切线.
(2)解:∵
∴
∴
∵
∴
又∵
∴
∴即
解得
∵,
∵
∴
在中,
【解析】【分析】(1)连接OC,由圆周角定理可得∠ACB=90°,由垂直的概念可得∠AEC=∠AFC=90°,利用HL证明△AEC≌△AFC,得到∠EAC=∠FAC,由等腰三角形的性质可得∠ACO=∠FAC,结合∠EAC+∠ECA=90°可得OC⊥AE,据此证明;
(2)由同角的余角相等可得∠ACO=∠BCD,由等腰三角形的性质可得∠CAD=∠ACO,则∠CAD=∠BCD,由两角对应相等的两个三角形相似可得△BCD∽△CAD,利用相似三角形的性质求出CD的值,由OD=OB+BD可得OD,利用三角函数的概念可得DE,然后由勾股定理就可求出AE.
18.【答案】(1)解:过点A作AE⊥x轴于点E,如图
∵tan∠AOC=1,A(1,m),B(n,﹣2)
∴m=1
∴1=
∴k=2
∴﹣2=
∴n=﹣
∴A(1,1),B(﹣,﹣2)
把A(1,1),B(﹣,﹣2)分别代入y=ax+b得:
解得
∴y=2x﹣1
∴k,a,b的值分别为2,2,﹣1.
(2)解:∵y=2x﹣1
∴当x=0时,y=﹣1,即D(0,﹣1)
∴S△AOB=OD×xA+OD×(﹣xB)
=OD×(xA﹣xB)
=×1×(1+)
=
∴△AOB的面积为.
【解析】【分析】(1)过点A作AE⊥x轴于点E,tan∠AOC=1,利用点A的坐标,可求出m的值,代入函数解析式,可求出k的值,即可得到函数解析式,从而可求出n的值,可得到点B的坐标,然后将点A,B的坐标分别代入一次函数解析式,可得到关于a,b的方程组,解方程组求出a,b的值,即可得到一次函数解析式.
(2)利用一次函数解析式求出点D的坐标,再利用三角形的面积公式求出△AOB的面积.
19.【答案】(1)证明:∵PD为⊙O的直径,PD⊥BC,
∴BC为⊙O的切线,
∴∠EFP=∠EPB
(2)解:①∵∠APB=4∠APD,∠APB=90°+∠APD,
∴4∠APD=90°+∠APD,
∴∠APD=30°.
∴∠APC=90°﹣∠APD=60°.
∵AB=20,sinB=,
∴AC=AB sinB=20×=12.
∵tan∠APC==,
∴PC= =4;
②当EF=EP时,
∵EF=EP,
∴∠EPF=∠EFP,
∵∠EFP=∠EPB,
∴∠EPF=∠EPB.
∵PD为⊙O的直径,
∴PE⊥AB.
∴∠BEP=∠AEP=90°,
在△BEP和△AEP中,
∴△BEP≌△AEP(ASA),
∴BE=AE=10.
∵sinB=,
∴tanB==,
∴PE=;
当EP=FP时,
∵EP=FP,
∴,
∵PD为⊙O的直径,
∴PD⊥EF,
∵PD⊥BC,
∴EF∥BC.
∴∠B=∠AEF,
∵∠AEF=∠DPF,
∴∠B=∠DPF.
∵PD⊥EF,AC⊥BC,
∴DP∥AC,
∴∠DPF=∠PAC,
∴∠PAC=∠B.
∴tan∠PAC=tanB==.
∴PC=9.
∴PB=BC﹣PC=7.
∵sinB==
∴PE=;
当FE=PF时,
∵FE=PF,
∴∠FEP=∠FPE.
∵FEP+∠AEF=90°,∠FPE+∠FAE=90°,
∴∠AEF=∠FAE,
∴EF=AF.
∴AF=FP=EF.
∵∠DPA=∠AEF,
∴∠DPA=∠DAP,
∴PD=AD.
设PD=AD=3x,
∵sinB==,
∴BD=5x.
∴AB=BD+AD=8x=20,
∴X=.
∴BD=5x=.
∵cosB=,
∴BP=10.
∴PC=BC﹣BP=6.
∴AP= = 6.
∴PF=AP=3.
综上,当△PEF为等腰三角形时,满足条件的△PEF的腰长为3或或.
(3)
【解析】【解答】解:(3)当D,F,C在一条直线上时,
∵PD为⊙O的直径,
∴PF⊥CD,
∴∠FAC+∠FCA=90°,
∵∠FCP+∠FCA=90°,
∴∠FAC=∠FCP.
∵∠ACP=∠DPC=90°,
∴△ACP∽△CPD.
∴
∴PC2=AC PD.
∵sinB= ,
∴∠B=45°.
∴BC=AC,PD=PB.
∴PC=BC﹣BP=AC﹣PD.
∴(AC﹣PD)2=AC PD,
∴DP2﹣3DP AC+AC2=0.
解得:DP= AC或DP=AC(不合题意,舍去).
∴= ,
故答案为:
【分析】(1)利用PD为⊙O的直径,PD⊥BC,可证得CB是圆O的切线,再利用弦切角定理可证得结论.
(2)①利用已知可得到4∠APD=90°+∠APD,可求出∠APD=30°,从而可求出∠APC的度数,利用解直角三角形求出AB、AC、PC的长;②利用△PEF是等腰三角形,分情况讨论:当EF=EP时,由EF=EP,可推出∠EPF=∠EFP,由此可证得∠EPF=∠EPB,利用圆周角定理求出∠BEP=∠AEP=90°,利用ASA证明△BEP≌△AEP,利用全等三角形的性质可求出AE的长;再利用解直角三角形求出PE的长;当EP=FP时,由EP=PF,可证得,利用垂径定理可证得PD⊥EF,由此可推出EF∥BC,利用平行线的性质可证得∠B=∠AEF=∠DPF;再证明DP∥AC,可得到∠DPF=∠PAC=∠B,利用解直角三角形求出PC的长,根据PB=BC-PC,代入计算求出PB的长,利用解直角三角形求出PE的长;当FE=PF时,利用等边对等角可证得∠FEP=∠FPE,利用余角的性质可证得∠AEF=∠FAE,利用等角对等边可得到EF=AF=FP,从而可推出PD=AD=2x,利用解直角三角形表示出BD的长,根据AB=BD+AD,据此可得到关于x的方程,解方程求出x的值可求出BD,BP的长,继而可求出PC的长,利用勾股定理求出AP的长,然后求出PF的长;综上所述可得到符合题意的PF的长.
