人教版数学七年级下学期期末素质提升训练卷(二)(含解析)
文档属性
| 名称 | 人教版数学七年级下学期期末素质提升训练卷(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 17:45:11 | ||
图片预览



文档简介
七年级下学期期末素质提升训练卷(二)
时间:120分钟 满分:120分
一、单选题(共30分)
1.(本题3分)的平方根是( )
A. B. C. D.
2.(本题3分)下列调查中,适宜采用全面调查方式的是( )
A.了解某种灯泡的使用寿命 B.了解一批冷饮的质量是否合格
C.检测神舟十九号飞船的零件 D.了解全国九年级学生的视力情况
3.(本题3分)在实数,,,,,,0中,无理数有( )个
A.2 B.3 C.4 D.5
4.(本题3分)如图,小明告诉小华图中两点的坐标分别为,小华一下就说出了点的正确坐标,那么小华说出的点的坐标是( )
A. B. C. D.
5.(本题3分)某工厂用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等),做成如图2所示的A种与B种两种长方体形状的无盖纸盒.现有正方形纸板180张,长方形纸板340张,刚好全部用完若设能做成x个A型盒子y个B型盒子则以下列出的方程组中正确的为( )
A. B. C. D.
6.(本题3分)不等式组的解集是( )
A. B. C.或 D.
7.(本题3分)点,分别在x轴的负半轴和y轴的正半轴上,,,将线段平移至,若点,的坐标分别为,,则( )
A.1 B. C. D.
8.(本题3分)在解关于x、y的方程组时甲看错①中的a,解得,,乙看错②中的b,解得,,则a和b的正确值应是( )
A., B.,
C., D.,
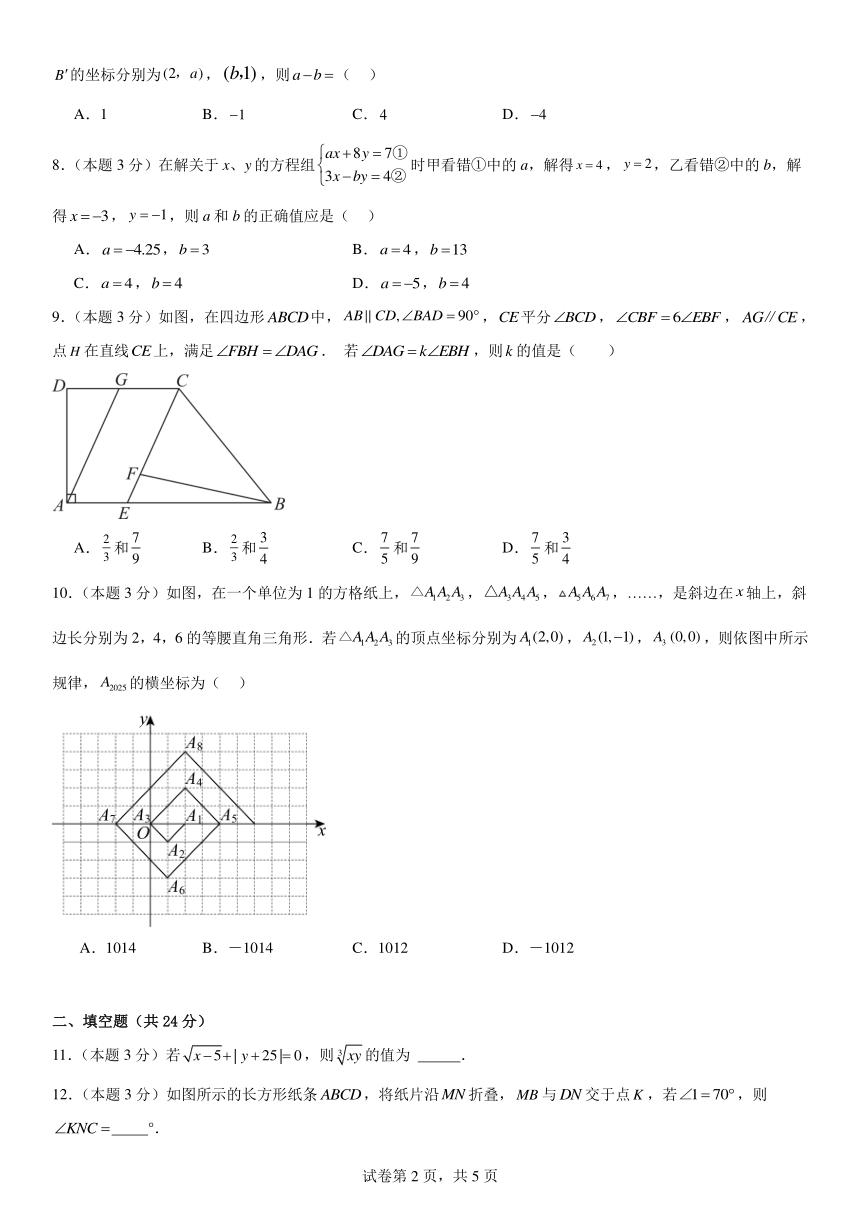
9.(本题3分)如图,在四边形中,,平分,,,点在直线上,满足. 若,则的值是( )
A.和 B.和 C.和 D.和
10.(本题3分)如图,在一个单位为1的方格纸上,,,,……,是斜边在轴上,斜边长分别为2,4,6的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的横坐标为( )
A.1014 B.-1014 C.1012 D.-1012
二、填空题(共24分)
11.(本题3分)若,则的值为 .
12.(本题3分)如图所示的长方形纸条,将纸片沿折叠,与交于点,若,则 °.
13.(本题3分)已知满足方程组,则 .
14.(本题3分)古代有个数学问题:“5头牛,2只羊,值金12两;2头牛,5只羊,值金9两.问每头牛,每只羊各值金多少两?”则问题中每头牛值金 两.
15.(本题3分)几个小朋友分糖,若每个小朋友分4块,则剩余6块糖.若每个小朋友分6块,则最后一个小朋友分有糖但不足3块.则共有糖 块.
16.(本题3分)在平面直角坐标系中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,)称为点P的“倒影点”.若点A在x轴的下方,且点A的“倒影点”A′与点A是同一个点,则点A的坐标为 .
17.(本题3分)已知关于x,y的方程组和的解相同,则的值为 .
18.(本题3分)对非负实数“四舍五入”到个位的值记为,即:当为非负整数时,如果,则如:,.
(1)如果,则的取值范围为 ;
(2)如果,则 .
三、解答题(共66分)
19.(本题6分)计算:
(1). (2).
20.(本题6分)解方程组:
(1) (2)
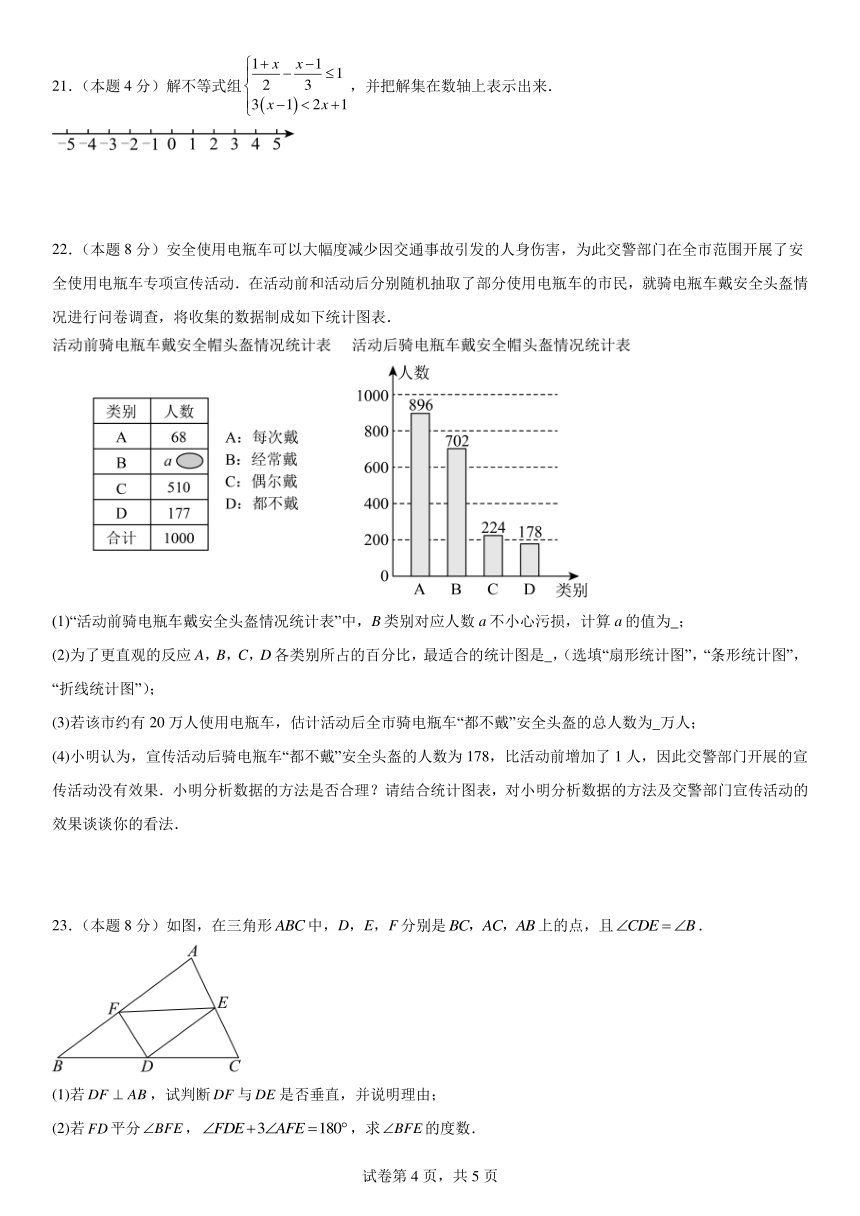
21.(本题4分)解不等式组,并把解集在数轴上表示出来.
22.(本题8分)安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全头盔情况进行问卷调查,将收集的数据制成如下统计图表.
(1)“活动前骑电瓶车戴安全头盔情况统计表”中,B类别对应人数a不小心污损,计算a的值为 ;
(2)为了更直观的反应A,B,C,D各类别所占的百分比,最适合的统计图是 ,(选填“扇形统计图”,“条形统计图”,“折线统计图”);
(3)若该市约有20万人使用电瓶车,估计活动后全市骑电瓶车“都不戴”安全头盔的总人数为 万人;
(4)小明认为,宣传活动后骑电瓶车“都不戴”安全头盔的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
23.(本题8分)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
24.(本题10分)作图:
(1)请建立合适的平面直角坐标,使两点的坐标分别是
(2)在(1)的条件下,平移线段到使点的对应点为格点,点对应点为点
①请画出线段
②连接,格点在上,请在线段上找点使得
③在轴上确定一点,使,则满足条件的点的坐标为______.
25.(本题12分)某公司计划购买A,B两种型号的打印机共20台,通过市场调研发现,购买3台A型打印机和4台B型打印机需6180元,购买4台A型打印机和6台B型打印机需8840元.
(1)购买A,B两种型号打印机每台的价格分别是多少元?
(2)根据公司实际情况,要求购买A型打印机的数量不超过B型打印机数量的一半,且购买这两种型号打印机的总费用不能超过17800元,该公司按计划购买A,B两种型号打印机共有几种购买方案?
(3)在(2)的条件下,哪种方案费用最低?并求出最低费用.
26.(本题12分)在平面直角坐标系中,点,,,且,,满足.
(1)请用含的式子分别表示,两点的坐标;
(2)当实数变化时,判断的面积是否发生变化?若不变,求其值;若变化,求其变化范围;
(3)如图,已知线段与轴相交于点,直线与直线交于点,若,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题主要考查了求一个数的算术平方根和平方根,对于两个实数a、b若满足,那么a就叫做b的平方根,若a为非负数,那么a就叫做b的算术平方根,据此求解即可.
【详解】解:,
∵9的平方根为,
∴的平方根是,
故选:A.
2.C
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A.了解某种灯泡的使用寿命,适合采用抽样调查的方式,故本选项不合题意;
B.了解一批冷饮的质量是否合格,适合采用抽样调查的方式,故本选项不合题意;
C.检测神舟十九号飞船的零件,适合采用普查的方式,故本选项符合题意;
D.了解全国九年级学生的视力情况,适合采用抽样调查的方式,故本选项不合题意.
故选:C.
3.C
【分析】本题考查了无理数的概念,准确掌握无理数的概念是解题的关键.
根据无限不循环的小数是无理数判断即可.
【详解】解:∵
∴,,0是有理数,
,,,是无理数,共4个;
故选:C.
4.D
【分析】本题考查了点坐标的平移.熟练掌握:点坐标平移,左减右加,上加下减是解题的关键.
由点向右平移2个单位,向上平移两个单位得点,求解作答即可.
【详解】∵图中两点的坐标分别为,
∴每格长度为1,
∵点向右平移2个单位,向上平移两个单位得点,
∴,
故选:D.
5.B
【分析】根据无盖纸盒的长方形和正方形纸板关系得到方程组即可.
【详解】解:因为能做成x个A型盒子,y个B型盒子,
根据A种长方体形状的无盖纸盒需要1个正方形、4个长方形,B种长方体形状的无盖纸盒需要2个正方形和3个长方形,
正方形和纸板180张,长方形纸板340张,刚好全部用完,
所以可以列出方程组:.
故选:B.
【点睛】本题考查二元一次方程组的实际应用,解题的关键是找到等量关系列出方程.
6.D
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】解:,
解不等式①,得,
解不等式②,得,
故不等式组的解集为.
故选:D.
7.D
【分析】本题考查直角坐标系中的平移,由题意,线段由线段向右平移个单位,再向下平移个单位得到,即可得出、的值,即可得出答案.
【详解】解:如图
、的坐标分别为和,、的坐标分别为和,
线段由线段向右平移个单位,再向下平移个单位得到,
;
;
.
故选:D.
8.D
【分析】本题主要考查了二元一次方程组的错解问题,正确理解题意是解题的关键.甲看错了a,则甲的结果满足方程②,乙看错了b,则乙的结果满足方程①,由此建立关于a、b的方程求解即可.
【详解】解:∵解关于x、y的方程组时甲看错①中的a,解得,,乙看错②中的b,解得,,
∴把,代入②,得,
解得:,
把,,代入①,得,
解得:,
∴,
故选:D.
9.C
【分析】本题主要考查了平行线的性质、角平分线的定义等知识点,正确作出辅助线和灵活运用分类讨论思想成为解答本题的关键.
分类讨论:①当点H在点F的上方时,设,根据时平行线的性质和垂直的性质可得、,再根据角平分线的性质可得即,再结合可得,然后可得,再根据列式即可求得k;同理可求,②当点H在点F的下方时k的值.
【详解】解:如图,当点H在点F的上方时,设,
,
,
,
,
平分,
,
,
,
,
,
,
,
,
;
当点H在点F的下方时,
,
,
,
,
,
平分,
,
,
,
,
,
,
,
,
.
故选:C.
10.A
【分析】本题主要考查了点的坐标规律探索,解题的关键是根据点的坐标的变化寻找规律.根据脚码确定出当脚码分别为偶数和奇数时的坐标规律,即可得到答案.
【详解】解:由图可得:
∵,,,,, ,
∴得到规律,
当为奇数时:;
当为偶数时:;
∵,
∴,
∴.
故选:A.
11.
【分析】根据算术平方根及绝对值的非负性求得x,y的值,然后利用立方根的定义即可求得答案.本题考查算术平方根及绝对值的非负性,立方根,结合已知条件求得x,y的值是解题的关键.
【详解】解:∵,
∴,
∴,
∴,
故答案为:.
12.
【分析】本题考查折叠和平行线的知识,解题的关键是掌握折叠的性质,平行线的性质,根据图形折叠,则,根据平行线的性质,则,,即可求出.
【详解】由折叠得,,
∵是长方形,
∴,
∴,,
∵,
∴,,
∴,
∵,
∴,
∴.
故答案为:.
13.
【分析】本题考查了解二元一次方程组,代数式求值,将原方程组中的两个方程相加得到,即,再整体代入代数式计算即可求解,掌握整体代入法是解题的关键.
【详解】解:将方程组中的两个方程相加得,,
即,
∴,
故答案为:.
14.2
【分析】本题考查的知识点是二元一次方程组的实际应用,解此题的关键是根据题目找出等量关系式.
设每头牛值金x两,每只羊值金y两,根据“5头牛,2只羊,值金12两;2头牛,5只羊,值金9两”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设每头牛值金x两,每只羊值金y两,
依题意,得:,
解得:.
∴每头牛值金2两.
故答案为:2.
15.26
【分析】设一共有x个小朋友,则一共有块糖,根据题意可得,求出x的整数解,再求出的值,即可得糖的总块数。
本题考查了一元一次不等式组的应用,解决问题的关键是读懂题意,正确列出不等式进行求解.
【详解】设一共有x个小朋友,则一共有块糖,由题意得
,
解得,
∵x为正整数,
,
,
∴共有糖26块。
故答案为:26
16.(1,﹣1),(﹣1,﹣1).
【分析】根据不在坐标轴上的任意一点P (x, y) , 我们把点P (,)称为点P的“倒影点”,可得答案.
【详解】解:若点A在x轴的下方,且点A的“倒影点” A'与点A是同一个点,
可得:,,可得x=,y=,
点A在x轴的下方
则点A的坐标为(1,-1),(-1,-1),
故答案为: (1,-1),(-1,-1).
【点睛】本题主要考查象限及点的坐标的有关性质.
17.1
【分析】本题考查的是同解方程组,二元一次方程组的解法,利用同解的含义重组方程组是解题的关键.把方程组中的两个已知方程组合可得,解方程组可得:,再代入另外两个方程,求解 从而可得答案.
【详解】解:根据题意得:
①②:
把代入①:
把代入得
解得:
;
故答案为:
18.
【分析】本题考查近似数和有效数字、新定义,解答本题的关键是明确题意,利用新定义解答.
(1)根据题意可以得到,然后求解即可;
(2)根据题意可以得到,且为非负整数,然后求解即可.
【详解】解:(1),
,
解得:,
故答案为:;
(2),
,
∴
且为非负整数,
解得:,
故答案为:.
19.(1)
(2)1
【分析】(1)根据立方根,算术平方根计算即可.
(2)根据立方根,绝对值计算即可.
本题考查了实数的混合运算,熟练掌握相关定义和实数的运算法则是解题的关键.
【详解】(1)
.
(2)
.
20.(1)
(2)
【分析】本题考查了二元一次方程组.
(1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
【详解】(1)
得,
得,
把代入②得,,
,
所以原方程组的解是;
(2)
得
将代入①得
∴原方程组的解为:.
21.,把解集在数轴上表示见解析
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:,
∴表示在数轴上为:
22.(1)245
(2)扇形统计图
(3)
(4)不合理,理由见解析
【分析】本题考查了条形统计图、扇形统计图、统计表以及用样本估计总体:
(1)用总人数减去其他类别的人数即可;
(2)根据三种统计图的特点选择即可;
(3)活动前全市骑电车“都不戴”安全帽的总人数等于在抽取的市民中“都不戴”的人数占抽取人数的百分比乘以20万;
(4)先求出宣传活动前“都不戴”安全帽的百分比,再求出宣传活动后“都不戴”安全帽的百分比,比较大小可得到交警部门开展的宣传活动有效果;
掌握三种统计图的特点是解题的关键.
【详解】(1)解:由题可得:,
故答案为:;
(2)解:为了更直观的反应A,B,C,D各类别所占的百分比,最适合的统计图是扇形统计图,
故答案为:扇形统计图;
(3)解:活动后全市骑电瓶车“都不戴”安全头盔的总人数为:
万人。
故答案为:;
(4)解:小明分析数据的方法不合理,理由如下:
宣传活动前“都不戴”安全帽的百分比:,
宣传活动后“都不戴”安全帽的百分比:,
∵,
∴交警部门开展的宣传活动有效果.
23.(1),理由见详解
(2)
【分析】(1)结论:.证明,可得,再证明即可解决问题.
(2)根据已知条件,构建方程求出即可.
本题考查等腰三角形的判定和性质,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【详解】(1)解:结论:.
理由:,
,
,
,
,
,
.
(2)解:平分,
,
,
,
,
,
,
,
.
24.(1)见解析
(2)①见解析;②见解析;③或
【分析】本题考查了坐标与图形,平移作图,平移的性质;
(1)根据题意建立平面直角坐标系,即可求解;
(2)①根据平移方式,将点向右平移1个单位,再向上平移3个单位得到,连接,即可求解;
②根据①的平移方式将点平移至,连接交于点,则;
③根据三角形的面积公式即可求解.
【详解】(1)如图所示,
(2)解:①如图所示,即为所求,
②如图所示,
③如图所示
设,
∵,
∴
即
解得:
∴或
25.(1)购买种型号打印机每台的价格是860元,购买种型号打印机每台的价格是900元;
(2)共有两种购买方案;
(3)购买种型号打印机6台,购买种型号打印机14台,费用最低,最低费用为17760元.
【分析】本题考查了二元一次方程组和一元一次不等式组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式组求解.
(1)设购买种型号打印机每台的价格是元,购买种型号打印机每台的价格是元,根据购买3台型打印机和4台型打印机需6180元;购买4台型打印机和6台型打印机需8840元列方程组求解;
(2)设购买种型号打印机台,则购买种型号打印机台,根据题意可列出不等式组求解.
(3)根据求出的购买方案直接计算可得出答案.
【详解】(1)解:设购买种型号打印机每台的价格是元,购买种型号打印机每台的价格是元,依题意有:
,
解得.
故购买种型号打印机每台的价格是860元,购买种型号打印机每台的价格是900元;
(2)解:设购买种型号打印机台,则购买种型号打印机台,依题意有:
,
解得:.
故共有两种购买方案:
购买种型号打印机5台,购买种型号打印机15台;
购买种型号打印机6台,购买种型号打印机14台;
(3)解:若购买种型号打印机5台,购买种型号打印机15台,费用为(元;
若购买种型号打印机6台,购买种型号打印机14台,费用为(元;
,
购买种型号打印机6台,购买种型号打印机14台,费用最低,最低费用为17760元.
26.(1),;(2)不变,值为;(3)
【分析】(1)先解方程组,用含a的式子表示b、c的值,进而可得点A,B,C的坐标.
(2)根据S△ABC=S梯形AFGB+S梯形BGHC S梯形AFHC代入数据计算即可.
(3)先解方程组用含a的代数式表示出b,c,根据线段AB在与y轴相交于点E可得关于a的不等式组,解即可得a的一个取值范围,再由2PA≤PC可得2S△AOB≤△S△BOC,然后用含a的代数式表示出2S△AOB与△S△BOC,进而可得关于a的不等式,解不等式可得a的一另个取值范围,从而可得结果.
【详解】解:(1)解方程组,得,
,,
(2)的面积不变,值为
如图,过点,,分别作轴的垂线,垂足分别为,,,
∵,,,
∴,,,,,,
∴
;
(3)连接,,
∵,,,
又∵线段在与轴相交于点,
∴,,
∴,
∵,
∴,,
∴2,
如图,过点,,分别作轴的垂线,垂足分别为,,,
∵,
,
,
∴,解得,
∴实数的取值范围是.
【点睛】本题属于三角形综合题,考查三角形的面积,解二元一次方程组,坐标与图形的性质,平移的性质等知识,涉及的知识点多,综合性强,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
答案第1页,共2页
答案第1页,共2页
时间:120分钟 满分:120分
一、单选题(共30分)
1.(本题3分)的平方根是( )
A. B. C. D.
2.(本题3分)下列调查中,适宜采用全面调查方式的是( )
A.了解某种灯泡的使用寿命 B.了解一批冷饮的质量是否合格
C.检测神舟十九号飞船的零件 D.了解全国九年级学生的视力情况
3.(本题3分)在实数,,,,,,0中,无理数有( )个
A.2 B.3 C.4 D.5
4.(本题3分)如图,小明告诉小华图中两点的坐标分别为,小华一下就说出了点的正确坐标,那么小华说出的点的坐标是( )
A. B. C. D.
5.(本题3分)某工厂用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等),做成如图2所示的A种与B种两种长方体形状的无盖纸盒.现有正方形纸板180张,长方形纸板340张,刚好全部用完若设能做成x个A型盒子y个B型盒子则以下列出的方程组中正确的为( )
A. B. C. D.
6.(本题3分)不等式组的解集是( )
A. B. C.或 D.
7.(本题3分)点,分别在x轴的负半轴和y轴的正半轴上,,,将线段平移至,若点,的坐标分别为,,则( )
A.1 B. C. D.
8.(本题3分)在解关于x、y的方程组时甲看错①中的a,解得,,乙看错②中的b,解得,,则a和b的正确值应是( )
A., B.,
C., D.,
9.(本题3分)如图,在四边形中,,平分,,,点在直线上,满足. 若,则的值是( )
A.和 B.和 C.和 D.和
10.(本题3分)如图,在一个单位为1的方格纸上,,,,……,是斜边在轴上,斜边长分别为2,4,6的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的横坐标为( )
A.1014 B.-1014 C.1012 D.-1012
二、填空题(共24分)
11.(本题3分)若,则的值为 .
12.(本题3分)如图所示的长方形纸条,将纸片沿折叠,与交于点,若,则 °.
13.(本题3分)已知满足方程组,则 .
14.(本题3分)古代有个数学问题:“5头牛,2只羊,值金12两;2头牛,5只羊,值金9两.问每头牛,每只羊各值金多少两?”则问题中每头牛值金 两.
15.(本题3分)几个小朋友分糖,若每个小朋友分4块,则剩余6块糖.若每个小朋友分6块,则最后一个小朋友分有糖但不足3块.则共有糖 块.
16.(本题3分)在平面直角坐标系中,对于不在坐标轴上的任意一点P(x,y),我们把点P′(,)称为点P的“倒影点”.若点A在x轴的下方,且点A的“倒影点”A′与点A是同一个点,则点A的坐标为 .
17.(本题3分)已知关于x,y的方程组和的解相同,则的值为 .
18.(本题3分)对非负实数“四舍五入”到个位的值记为,即:当为非负整数时,如果,则如:,.
(1)如果,则的取值范围为 ;
(2)如果,则 .
三、解答题(共66分)
19.(本题6分)计算:
(1). (2).
20.(本题6分)解方程组:
(1) (2)
21.(本题4分)解不等式组,并把解集在数轴上表示出来.
22.(本题8分)安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全头盔情况进行问卷调查,将收集的数据制成如下统计图表.
(1)“活动前骑电瓶车戴安全头盔情况统计表”中,B类别对应人数a不小心污损,计算a的值为 ;
(2)为了更直观的反应A,B,C,D各类别所占的百分比,最适合的统计图是 ,(选填“扇形统计图”,“条形统计图”,“折线统计图”);
(3)若该市约有20万人使用电瓶车,估计活动后全市骑电瓶车“都不戴”安全头盔的总人数为 万人;
(4)小明认为,宣传活动后骑电瓶车“都不戴”安全头盔的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
23.(本题8分)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
24.(本题10分)作图:
(1)请建立合适的平面直角坐标,使两点的坐标分别是
(2)在(1)的条件下,平移线段到使点的对应点为格点,点对应点为点
①请画出线段
②连接,格点在上,请在线段上找点使得
③在轴上确定一点,使,则满足条件的点的坐标为______.
25.(本题12分)某公司计划购买A,B两种型号的打印机共20台,通过市场调研发现,购买3台A型打印机和4台B型打印机需6180元,购买4台A型打印机和6台B型打印机需8840元.
(1)购买A,B两种型号打印机每台的价格分别是多少元?
(2)根据公司实际情况,要求购买A型打印机的数量不超过B型打印机数量的一半,且购买这两种型号打印机的总费用不能超过17800元,该公司按计划购买A,B两种型号打印机共有几种购买方案?
(3)在(2)的条件下,哪种方案费用最低?并求出最低费用.
26.(本题12分)在平面直角坐标系中,点,,,且,,满足.
(1)请用含的式子分别表示,两点的坐标;
(2)当实数变化时,判断的面积是否发生变化?若不变,求其值;若变化,求其变化范围;
(3)如图,已知线段与轴相交于点,直线与直线交于点,若,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题主要考查了求一个数的算术平方根和平方根,对于两个实数a、b若满足,那么a就叫做b的平方根,若a为非负数,那么a就叫做b的算术平方根,据此求解即可.
【详解】解:,
∵9的平方根为,
∴的平方根是,
故选:A.
2.C
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A.了解某种灯泡的使用寿命,适合采用抽样调查的方式,故本选项不合题意;
B.了解一批冷饮的质量是否合格,适合采用抽样调查的方式,故本选项不合题意;
C.检测神舟十九号飞船的零件,适合采用普查的方式,故本选项符合题意;
D.了解全国九年级学生的视力情况,适合采用抽样调查的方式,故本选项不合题意.
故选:C.
3.C
【分析】本题考查了无理数的概念,准确掌握无理数的概念是解题的关键.
根据无限不循环的小数是无理数判断即可.
【详解】解:∵
∴,,0是有理数,
,,,是无理数,共4个;
故选:C.
4.D
【分析】本题考查了点坐标的平移.熟练掌握:点坐标平移,左减右加,上加下减是解题的关键.
由点向右平移2个单位,向上平移两个单位得点,求解作答即可.
【详解】∵图中两点的坐标分别为,
∴每格长度为1,
∵点向右平移2个单位,向上平移两个单位得点,
∴,
故选:D.
5.B
【分析】根据无盖纸盒的长方形和正方形纸板关系得到方程组即可.
【详解】解:因为能做成x个A型盒子,y个B型盒子,
根据A种长方体形状的无盖纸盒需要1个正方形、4个长方形,B种长方体形状的无盖纸盒需要2个正方形和3个长方形,
正方形和纸板180张,长方形纸板340张,刚好全部用完,
所以可以列出方程组:.
故选:B.
【点睛】本题考查二元一次方程组的实际应用,解题的关键是找到等量关系列出方程.
6.D
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】解:,
解不等式①,得,
解不等式②,得,
故不等式组的解集为.
故选:D.
7.D
【分析】本题考查直角坐标系中的平移,由题意,线段由线段向右平移个单位,再向下平移个单位得到,即可得出、的值,即可得出答案.
【详解】解:如图
、的坐标分别为和,、的坐标分别为和,
线段由线段向右平移个单位,再向下平移个单位得到,
;
;
.
故选:D.
8.D
【分析】本题主要考查了二元一次方程组的错解问题,正确理解题意是解题的关键.甲看错了a,则甲的结果满足方程②,乙看错了b,则乙的结果满足方程①,由此建立关于a、b的方程求解即可.
【详解】解:∵解关于x、y的方程组时甲看错①中的a,解得,,乙看错②中的b,解得,,
∴把,代入②,得,
解得:,
把,,代入①,得,
解得:,
∴,
故选:D.
9.C
【分析】本题主要考查了平行线的性质、角平分线的定义等知识点,正确作出辅助线和灵活运用分类讨论思想成为解答本题的关键.
分类讨论:①当点H在点F的上方时,设,根据时平行线的性质和垂直的性质可得、,再根据角平分线的性质可得即,再结合可得,然后可得,再根据列式即可求得k;同理可求,②当点H在点F的下方时k的值.
【详解】解:如图,当点H在点F的上方时,设,
,
,
,
,
平分,
,
,
,
,
,
,
,
,
;
当点H在点F的下方时,
,
,
,
,
,
平分,
,
,
,
,
,
,
,
,
.
故选:C.
10.A
【分析】本题主要考查了点的坐标规律探索,解题的关键是根据点的坐标的变化寻找规律.根据脚码确定出当脚码分别为偶数和奇数时的坐标规律,即可得到答案.
【详解】解:由图可得:
∵,,,,, ,
∴得到规律,
当为奇数时:;
当为偶数时:;
∵,
∴,
∴.
故选:A.
11.
【分析】根据算术平方根及绝对值的非负性求得x,y的值,然后利用立方根的定义即可求得答案.本题考查算术平方根及绝对值的非负性,立方根,结合已知条件求得x,y的值是解题的关键.
【详解】解:∵,
∴,
∴,
∴,
故答案为:.
12.
【分析】本题考查折叠和平行线的知识,解题的关键是掌握折叠的性质,平行线的性质,根据图形折叠,则,根据平行线的性质,则,,即可求出.
【详解】由折叠得,,
∵是长方形,
∴,
∴,,
∵,
∴,,
∴,
∵,
∴,
∴.
故答案为:.
13.
【分析】本题考查了解二元一次方程组,代数式求值,将原方程组中的两个方程相加得到,即,再整体代入代数式计算即可求解,掌握整体代入法是解题的关键.
【详解】解:将方程组中的两个方程相加得,,
即,
∴,
故答案为:.
14.2
【分析】本题考查的知识点是二元一次方程组的实际应用,解此题的关键是根据题目找出等量关系式.
设每头牛值金x两,每只羊值金y两,根据“5头牛,2只羊,值金12两;2头牛,5只羊,值金9两”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设每头牛值金x两,每只羊值金y两,
依题意,得:,
解得:.
∴每头牛值金2两.
故答案为:2.
15.26
【分析】设一共有x个小朋友,则一共有块糖,根据题意可得,求出x的整数解,再求出的值,即可得糖的总块数。
本题考查了一元一次不等式组的应用,解决问题的关键是读懂题意,正确列出不等式进行求解.
【详解】设一共有x个小朋友,则一共有块糖,由题意得
,
解得,
∵x为正整数,
,
,
∴共有糖26块。
故答案为:26
16.(1,﹣1),(﹣1,﹣1).
【分析】根据不在坐标轴上的任意一点P (x, y) , 我们把点P (,)称为点P的“倒影点”,可得答案.
【详解】解:若点A在x轴的下方,且点A的“倒影点” A'与点A是同一个点,
可得:,,可得x=,y=,
点A在x轴的下方
则点A的坐标为(1,-1),(-1,-1),
故答案为: (1,-1),(-1,-1).
【点睛】本题主要考查象限及点的坐标的有关性质.
17.1
【分析】本题考查的是同解方程组,二元一次方程组的解法,利用同解的含义重组方程组是解题的关键.把方程组中的两个已知方程组合可得,解方程组可得:,再代入另外两个方程,求解 从而可得答案.
【详解】解:根据题意得:
①②:
把代入①:
把代入得
解得:
;
故答案为:
18.
【分析】本题考查近似数和有效数字、新定义,解答本题的关键是明确题意,利用新定义解答.
(1)根据题意可以得到,然后求解即可;
(2)根据题意可以得到,且为非负整数,然后求解即可.
【详解】解:(1),
,
解得:,
故答案为:;
(2),
,
∴
且为非负整数,
解得:,
故答案为:.
19.(1)
(2)1
【分析】(1)根据立方根,算术平方根计算即可.
(2)根据立方根,绝对值计算即可.
本题考查了实数的混合运算,熟练掌握相关定义和实数的运算法则是解题的关键.
【详解】(1)
.
(2)
.
20.(1)
(2)
【分析】本题考查了二元一次方程组.
(1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
【详解】(1)
得,
得,
把代入②得,,
,
所以原方程组的解是;
(2)
得
将代入①得
∴原方程组的解为:.
21.,把解集在数轴上表示见解析
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:,
∴表示在数轴上为:
22.(1)245
(2)扇形统计图
(3)
(4)不合理,理由见解析
【分析】本题考查了条形统计图、扇形统计图、统计表以及用样本估计总体:
(1)用总人数减去其他类别的人数即可;
(2)根据三种统计图的特点选择即可;
(3)活动前全市骑电车“都不戴”安全帽的总人数等于在抽取的市民中“都不戴”的人数占抽取人数的百分比乘以20万;
(4)先求出宣传活动前“都不戴”安全帽的百分比,再求出宣传活动后“都不戴”安全帽的百分比,比较大小可得到交警部门开展的宣传活动有效果;
掌握三种统计图的特点是解题的关键.
【详解】(1)解:由题可得:,
故答案为:;
(2)解:为了更直观的反应A,B,C,D各类别所占的百分比,最适合的统计图是扇形统计图,
故答案为:扇形统计图;
(3)解:活动后全市骑电瓶车“都不戴”安全头盔的总人数为:
万人。
故答案为:;
(4)解:小明分析数据的方法不合理,理由如下:
宣传活动前“都不戴”安全帽的百分比:,
宣传活动后“都不戴”安全帽的百分比:,
∵,
∴交警部门开展的宣传活动有效果.
23.(1),理由见详解
(2)
【分析】(1)结论:.证明,可得,再证明即可解决问题.
(2)根据已知条件,构建方程求出即可.
本题考查等腰三角形的判定和性质,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【详解】(1)解:结论:.
理由:,
,
,
,
,
,
.
(2)解:平分,
,
,
,
,
,
,
,
.
24.(1)见解析
(2)①见解析;②见解析;③或
【分析】本题考查了坐标与图形,平移作图,平移的性质;
(1)根据题意建立平面直角坐标系,即可求解;
(2)①根据平移方式,将点向右平移1个单位,再向上平移3个单位得到,连接,即可求解;
②根据①的平移方式将点平移至,连接交于点,则;
③根据三角形的面积公式即可求解.
【详解】(1)如图所示,
(2)解:①如图所示,即为所求,
②如图所示,
③如图所示
设,
∵,
∴
即
解得:
∴或
25.(1)购买种型号打印机每台的价格是860元,购买种型号打印机每台的价格是900元;
(2)共有两种购买方案;
(3)购买种型号打印机6台,购买种型号打印机14台,费用最低,最低费用为17760元.
【分析】本题考查了二元一次方程组和一元一次不等式组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式组求解.
(1)设购买种型号打印机每台的价格是元,购买种型号打印机每台的价格是元,根据购买3台型打印机和4台型打印机需6180元;购买4台型打印机和6台型打印机需8840元列方程组求解;
(2)设购买种型号打印机台,则购买种型号打印机台,根据题意可列出不等式组求解.
(3)根据求出的购买方案直接计算可得出答案.
【详解】(1)解:设购买种型号打印机每台的价格是元,购买种型号打印机每台的价格是元,依题意有:
,
解得.
故购买种型号打印机每台的价格是860元,购买种型号打印机每台的价格是900元;
(2)解:设购买种型号打印机台,则购买种型号打印机台,依题意有:
,
解得:.
故共有两种购买方案:
购买种型号打印机5台,购买种型号打印机15台;
购买种型号打印机6台,购买种型号打印机14台;
(3)解:若购买种型号打印机5台,购买种型号打印机15台,费用为(元;
若购买种型号打印机6台,购买种型号打印机14台,费用为(元;
,
购买种型号打印机6台,购买种型号打印机14台,费用最低,最低费用为17760元.
26.(1),;(2)不变,值为;(3)
【分析】(1)先解方程组,用含a的式子表示b、c的值,进而可得点A,B,C的坐标.
(2)根据S△ABC=S梯形AFGB+S梯形BGHC S梯形AFHC代入数据计算即可.
(3)先解方程组用含a的代数式表示出b,c,根据线段AB在与y轴相交于点E可得关于a的不等式组,解即可得a的一个取值范围,再由2PA≤PC可得2S△AOB≤△S△BOC,然后用含a的代数式表示出2S△AOB与△S△BOC,进而可得关于a的不等式,解不等式可得a的一另个取值范围,从而可得结果.
【详解】解:(1)解方程组,得,
,,
(2)的面积不变,值为
如图,过点,,分别作轴的垂线,垂足分别为,,,
∵,,,
∴,,,,,,
∴
;
(3)连接,,
∵,,,
又∵线段在与轴相交于点,
∴,,
∴,
∵,
∴,,
∴2,
如图,过点,,分别作轴的垂线,垂足分别为,,,
∵,
,
,
∴,解得,
∴实数的取值范围是.
【点睛】本题属于三角形综合题,考查三角形的面积,解二元一次方程组,坐标与图形的性质,平移的性质等知识,涉及的知识点多,综合性强,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
