人教版六年级数学下册 第三单元考点必刷试卷(含答案)
文档属性
| 名称 | 人教版六年级数学下册 第三单元考点必刷试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 18:23:09 | ||
图片预览

文档简介
第三单元考点必刷试卷
建议用时:80分钟满分:100+10分
考点一:圆柱和圆锥的认识
一、 填空题。 (每空1分,共13分)
1.圆柱的底面是相同的( ),圆柱的侧面是( ),展开是( )或( );圆柱的两个底面圆心之间的距离叫作( )。
2.圆锥的底面是( ),侧面展开是( ),从圆锥顶点到底面圆心的距离是圆锥的( )。
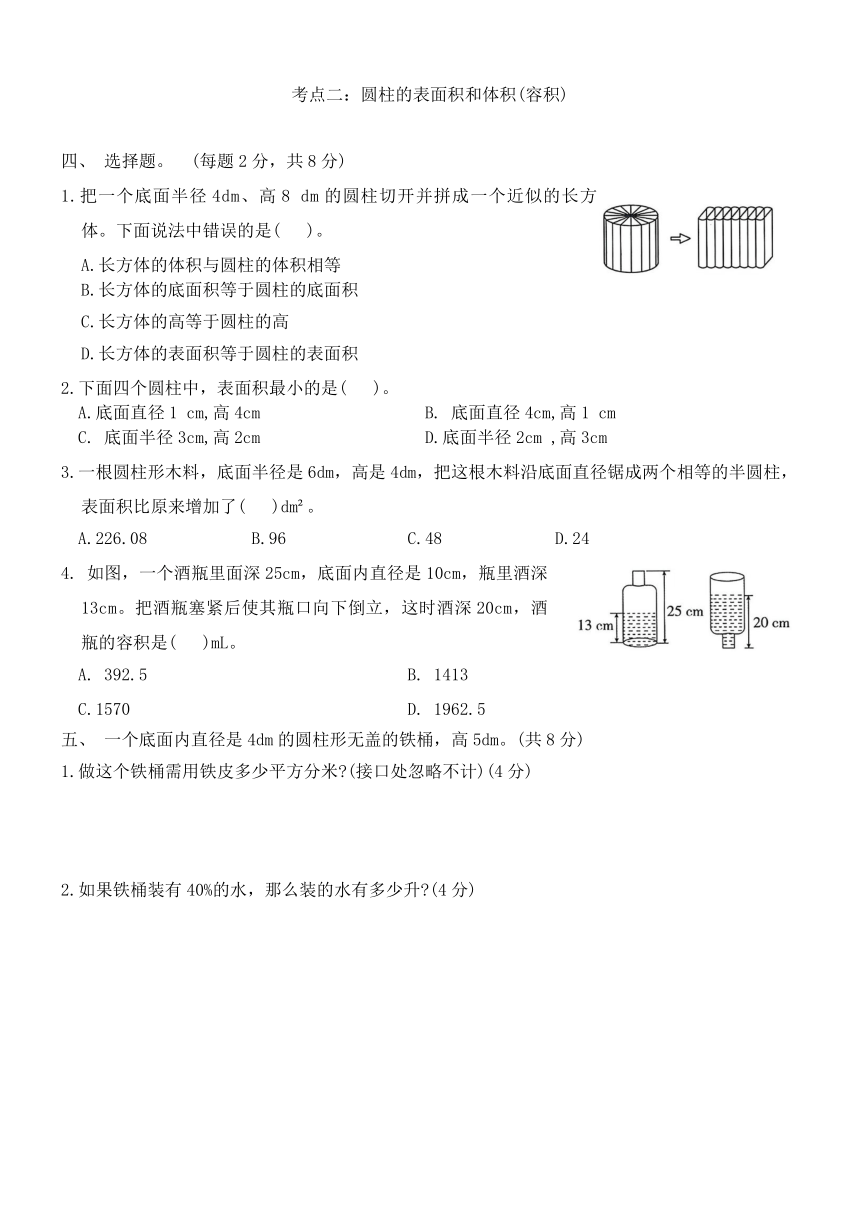
3.如图是四个纸板做成的圆柱,正确表示圆柱的高的是( )。(填序号)
4.如图,一个圆柱体食品罐,沿着虚线把侧面商标纸剪开,展开后得到一个面积为 的平行四边形,那么这个食品罐的底面周长是( )dm。
5.如图,以三角形中4 cm长的边为轴快速旋转,形成的立体图形是( ),这个立体图形的高是( ) cm,底面周长是( ) cm。
二、第1排中的平面图形分别绕其左侧边所在的直线旋转1 周能形成第2排的哪个立体图形 连一连。(8分)
三、 选择哪些材料恰好能做成圆柱形的盒子 (π值取3.14)(8分)
考点二:圆柱的表面积和体积(容积)
四、 选择题。 (每题2分,共8分)
1.把一个底面半径4dm、高8 dm的圆柱切开并拼成一个近似的长方体。下面说法中错误的是( )。
A.长方体的体积与圆柱的体积相等
B.长方体的底面积等于圆柱的底面积
C.长方体的高等于圆柱的高
D.长方体的表面积等于圆柱的表面积
2.下面四个圆柱中,表面积最小的是( )。
A.底面直径1 cm,高4cm B. 底面直径4cm,高1 cm
C. 底面半径3cm,高2cm D.底面半径2cm ,高3cm
3.一根圆柱形木料,底面半径是6dm,高是4dm,把这根木料沿底面直径锯成两个相等的半圆柱,表面积比原来增加了( )dm 。
A.226.08 B.96 C.48 D.24
4. 如图,一个酒瓶里面深25cm,底面内直径是10cm,瓶里酒深13cm。把酒瓶塞紧后使其瓶口向下倒立,这时酒深20cm,酒瓶的容积是( )mL。
A. 392.5 B. 1413
C.1570 D. 1962.5
五、 一个底面内直径是4dm的圆柱形无盖的铁桶,高5dm。(共8分)
1.做这个铁桶需用铁皮多少平方分米 (接口处忽略不计)(4分)
2.如果铁桶装有40%的水,那么装的水有多少升 (4分)
六、一个平面图形经过平移或旋转可以形成立体图形。例如,分别将长方形、圆作为底面,向上平移可以得到长方体、圆柱(如图①),它们的体积均可以用“底面积×高”进行计算;将一个长4cm,宽3cm的长方形,绕着长旋转一周,可以得到一个圆柱(如图②)。(共6分)
1.将一个底面直径( )cm 的圆作为底面,向上平移( )cm,也可以形成图②中的圆柱。(4分)
2.将一个两条直角边均为4cm的直角三角形作为底面,向上平移5cm,形成一个立体图形(如图③),它的体积是( )cm 。(2分)
考点三:圆锥的体积
七、 选择题。 (每题2分,共6分)
1.一张直角三角形纸片,分别以其中一条直角边为轴,旋转一周得到两个不同的圆锥(如图,单位:cm),形成的两个圆锥的体积相比,( )。
A. 甲<乙 B. 甲>乙
C. 甲=乙 D.无法比较
2.一个圆锥和一个圆柱的体积和底面积都相等,圆锥的高是24 cm,那么圆柱的高是( )cm。
A.8 B. 12 C. 24 D.72
3. 一个高为6cm的圆锥,沿高切开,表面积增加12 cm ,这个圆锥的体积是( )cm 。
A.24π B.8π C.6π D.2π
八、解决问题。 (共12分)
1.为求得一个圆锥形铁块的体积,小晨按如下步骤进行了操作:
(1)准备一个长方体容器,从里面量长12cm,宽8cm,高15cm。
(2)量得这个圆锥形铁块的高为8cm。
(3)往长方体容器中倒入一部分水后,将圆锥形铁块完全浸没在水中,水面上升1.5cm。根据以上信息,计算圆锥形铁块的体积。(6分)
2.某甜品店准备推出一款新口味的沙冰,为满足不同人群的需求,店家为这款沙冰设计了两种不同的包装(销售时要刚好盛满),两种包装的沙冰及其定价如图所示。你认为这样定价合理吗 请给出你的定价建议并用数据说明理由。(6分)
九、看图计算。 (共11分)
1.求圆锥体积时,忘记除以3 计算圆锥的体积。(单位:cm)(5分)
2.(解决表面积问题时,忽略了立体图形内部的面)求如图钢管的表面积。(单位:cm)(6分)
十、一个圆锥形沙堆,底面积是 ,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米 (10分)
十一、一个圆柱形木桶(如图),底面内直径为4d m,桶口距底面最小高度为5dm,最大高度为7 dm,现在木桶里水面高4.5 dm。将底面积是 的圆锥放进木桶(被水完全淹没),水溢出5.72 L。圆锥高多少厘米 (10分)
挑战题
小南用橡皮泥做了一个圆柱,他发现如果圆柱的底面直径增加2cm,高不变,侧面积就增加 。如果它的高增加3cm,底面直径不变,侧面积就增加 。这个圆柱原来的体积是多少立方厘米 (10分)
建议用时:80分钟满分:100+10分
考点一:圆柱和圆锥的认识
一、 填空题。 (每空1分,共13分)
1.圆柱的底面是相同的( ),圆柱的侧面是( ),展开是( )或( );圆柱的两个底面圆心之间的距离叫作( )。
2.圆锥的底面是( ),侧面展开是( ),从圆锥顶点到底面圆心的距离是圆锥的( )。
3.如图是四个纸板做成的圆柱,正确表示圆柱的高的是( )。(填序号)
4.如图,一个圆柱体食品罐,沿着虚线把侧面商标纸剪开,展开后得到一个面积为 的平行四边形,那么这个食品罐的底面周长是( )dm。
5.如图,以三角形中4 cm长的边为轴快速旋转,形成的立体图形是( ),这个立体图形的高是( ) cm,底面周长是( ) cm。
二、第1排中的平面图形分别绕其左侧边所在的直线旋转1 周能形成第2排的哪个立体图形 连一连。(8分)
三、 选择哪些材料恰好能做成圆柱形的盒子 (π值取3.14)(8分)
考点二:圆柱的表面积和体积(容积)
四、 选择题。 (每题2分,共8分)
1.把一个底面半径4dm、高8 dm的圆柱切开并拼成一个近似的长方体。下面说法中错误的是( )。
A.长方体的体积与圆柱的体积相等
B.长方体的底面积等于圆柱的底面积
C.长方体的高等于圆柱的高
D.长方体的表面积等于圆柱的表面积
2.下面四个圆柱中,表面积最小的是( )。
A.底面直径1 cm,高4cm B. 底面直径4cm,高1 cm
C. 底面半径3cm,高2cm D.底面半径2cm ,高3cm
3.一根圆柱形木料,底面半径是6dm,高是4dm,把这根木料沿底面直径锯成两个相等的半圆柱,表面积比原来增加了( )dm 。
A.226.08 B.96 C.48 D.24
4. 如图,一个酒瓶里面深25cm,底面内直径是10cm,瓶里酒深13cm。把酒瓶塞紧后使其瓶口向下倒立,这时酒深20cm,酒瓶的容积是( )mL。
A. 392.5 B. 1413
C.1570 D. 1962.5
五、 一个底面内直径是4dm的圆柱形无盖的铁桶,高5dm。(共8分)
1.做这个铁桶需用铁皮多少平方分米 (接口处忽略不计)(4分)
2.如果铁桶装有40%的水,那么装的水有多少升 (4分)
六、一个平面图形经过平移或旋转可以形成立体图形。例如,分别将长方形、圆作为底面,向上平移可以得到长方体、圆柱(如图①),它们的体积均可以用“底面积×高”进行计算;将一个长4cm,宽3cm的长方形,绕着长旋转一周,可以得到一个圆柱(如图②)。(共6分)
1.将一个底面直径( )cm 的圆作为底面,向上平移( )cm,也可以形成图②中的圆柱。(4分)
2.将一个两条直角边均为4cm的直角三角形作为底面,向上平移5cm,形成一个立体图形(如图③),它的体积是( )cm 。(2分)
考点三:圆锥的体积
七、 选择题。 (每题2分,共6分)
1.一张直角三角形纸片,分别以其中一条直角边为轴,旋转一周得到两个不同的圆锥(如图,单位:cm),形成的两个圆锥的体积相比,( )。
A. 甲<乙 B. 甲>乙
C. 甲=乙 D.无法比较
2.一个圆锥和一个圆柱的体积和底面积都相等,圆锥的高是24 cm,那么圆柱的高是( )cm。
A.8 B. 12 C. 24 D.72
3. 一个高为6cm的圆锥,沿高切开,表面积增加12 cm ,这个圆锥的体积是( )cm 。
A.24π B.8π C.6π D.2π
八、解决问题。 (共12分)
1.为求得一个圆锥形铁块的体积,小晨按如下步骤进行了操作:
(1)准备一个长方体容器,从里面量长12cm,宽8cm,高15cm。
(2)量得这个圆锥形铁块的高为8cm。
(3)往长方体容器中倒入一部分水后,将圆锥形铁块完全浸没在水中,水面上升1.5cm。根据以上信息,计算圆锥形铁块的体积。(6分)
2.某甜品店准备推出一款新口味的沙冰,为满足不同人群的需求,店家为这款沙冰设计了两种不同的包装(销售时要刚好盛满),两种包装的沙冰及其定价如图所示。你认为这样定价合理吗 请给出你的定价建议并用数据说明理由。(6分)
九、看图计算。 (共11分)
1.求圆锥体积时,忘记除以3 计算圆锥的体积。(单位:cm)(5分)
2.(解决表面积问题时,忽略了立体图形内部的面)求如图钢管的表面积。(单位:cm)(6分)
十、一个圆锥形沙堆,底面积是 ,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米 (10分)
十一、一个圆柱形木桶(如图),底面内直径为4d m,桶口距底面最小高度为5dm,最大高度为7 dm,现在木桶里水面高4.5 dm。将底面积是 的圆锥放进木桶(被水完全淹没),水溢出5.72 L。圆锥高多少厘米 (10分)
挑战题
小南用橡皮泥做了一个圆柱,他发现如果圆柱的底面直径增加2cm,高不变,侧面积就增加 。如果它的高增加3cm,底面直径不变,侧面积就增加 。这个圆柱原来的体积是多少立方厘米 (10分)
