沪科版七年级数学下册 10.3平行线的性质基础解答题(含答案)
文档属性
| 名称 | 沪科版七年级数学下册 10.3平行线的性质基础解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 263.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 20:04:00 | ||
图片预览




文档简介
沪科版七年级数学下册《10.3平行线的性质》基础解答题专题训练
1.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
2.完成下面的证明:
如图所示,AB⊥BF,∠CDF=90°,∠1=∠2,求证:∠3=∠E.
证明:∵AB⊥BF,
∴∠B= ( ).
∵∠CDF=90,
∴∠B=∠CDF,
∴AB∥CD( ).
∵∠1=∠2,
∴AB∥ ( ),
∴CD∥ ( ),
∴∠3=∠E( ).
3.如图,已知a∥b,∠3=∠4,那么直线c与直线d平行吗?请说明理由.
4.完成下面推理过程,并在括号中填写推理依据:
如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,试说明:AD平分∠BAC.
证明:∵AD⊥BC,EG⊥BC
∴∠ADC= =90°(垂直定义)
∴ ∥EG(同位角相等,两直线平行)
∴∠1= ( )
∠2=∠3( )
又∵∠3=∠E(已知)
∴ =∠2( )
∴AD平分∠BAC ( )
5.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
6.按要求完成下列证明:
已知:如图,DE∥BC,∠DEB=∠GFC.求证BE∥FG.
证明:∵DE∥BC;
∴∠DEB= ( ).
∵∠DEB=∠GFC.
∴ =∠GFC( ).
∴BE∥FG( ).
7.如图,已知∠C=∠5,∠1=∠2,那么AB∥CD,为什么?
请完成下列推理过程:
∵∠1=∠2(已知)
又∵∠2=∠BAC( )
∴∠BAC=∠1(等量代换)
∴ ∥ ( )
∴∠C=∠4( )
∵∠C=∠5(已知)
∴∠ =∠ ,(等量代换)
∴AB∥CD( )
8.如图,∠1=50°,∠2=130°,∠C=∠D.
(1)试说明:BD∥CE.
(2)探索∠A与∠F的数量关系,并说明理由.
9.如图,已知∠A=∠AGE,∠D=∠DGC.
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°.
10.如图在三角形ABC中,已知∠1+∠2=180°,∠3=∠B.
求证:∠AED=∠C.
11.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.
(1)直线EF与AB有怎样的位置关系?说明理由;
(2)若∠CEF=68°,则∠ACB的度数是多少?
12.完成下面的证明:
如图,已知∠1+∠2=180,∠A=∠C.求证:AD∥BC.
证明:∵∠1+∠2=180(已知),
∠2+∠CDB=180°(邻补角的定义),
∴∠CDB= (等角的补角相等).
∴DC∥ ( ).
∴∠C= ( ).
∵∠A=∠C(已知),
∴∠A= ( ).
∴AD∥BC( ).
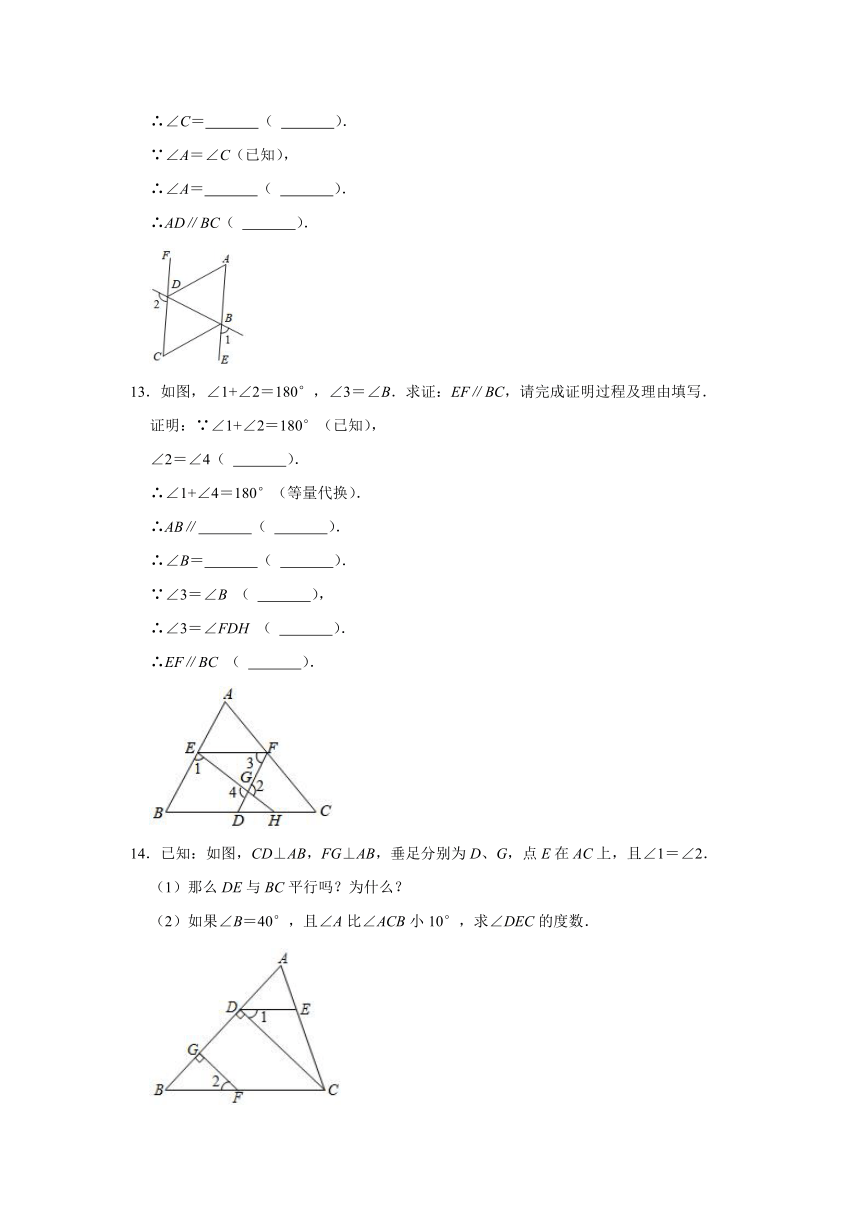
13.如图,∠1+∠2=180°,∠3=∠B.求证:EF∥BC,请完成证明过程及理由填写.
证明:∵∠1+∠2=180°(已知),
∠2=∠4( ).
∴∠1+∠4=180°(等量代换).
∴AB∥ ( ).
∴∠B= ( ).
∵∠3=∠B ( ),
∴∠3=∠FDH ( ).
∴EF∥BC ( ).
14.已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.
(1)那么DE与BC平行吗?为什么?
(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.
15.如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.
16.如图,已知AB⊥BC,DE⊥AB,∠1=∠2.
(1)请说明BD∥FG的理由.
(2)若D是AC的中点,F是BC的中点,已知AB=4,BC=3,求FG的长度.
17.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
18.如图,点E、F分别是AB、CD上的点,AC交DE、BF于点G、H,∠A=∠C,∠B=∠D.若∠1=62°,求∠2的度数.
19.如图,已知AB⊥BF,CD⊥BF,垂足分别为点B,D,∠BAF=∠AFE.求证:∠ACD=∠E.
20.完成下面的证明:
已知:如图,AB∥CD,CD和BE相交于点O,DE平分∠CDF,DE和BE相交于点E,∠E=∠2.
求证:∠B=2∠2.
证明:∵∠E=∠2(已知),
∴BE∥DF( ),
∴∠CDF=∠ (两直线平行,同位角相等).
又∵AB∥CD(已知),
∴∠B=∠ ( ),
∴∠B=∠CDF(等量代换).
∵DE平分∠CDF(已知),
∴∠CDF=2∠ (角平分线的定义).
∴∠B=2∠2( ).
21.如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°( ),
∴EF∥AD( ),
∴∠BEF= ( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴ (等量代换).
∴DG∥AB( ).
22.如图,点E、F分别是直线AB、CD上的点,分别连接AD、EC,交点为G,连接BF,与AD交于点H,若已知∠DHF=∠AGE,∠B=∠C试证明:∠A=∠D.
请根据题意将下面的解答过程补充完整:
解:∵∠DHF=∠AHB( ),
∠DHF=∠AGE(已知),
∴∠AHB=∠AGE( ),
∴BH∥ ( ),
∴∠B= (两直线平行,同位角相等).
∵∠B=∠C(已知),
∴ =∠C.
∴AB∥ ( ).
∴∠A=∠D( ).
23.如图所示,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°
(1)试判断AB与CD的位置关系,并说明理由;
(2)若∠2=36°,求∠3的度数.
24.完成下列证明:如图,已知∠ABC+∠ECB=180°,∠P=∠Q.
求证:∠1=∠2.
证明:∵∠ABC+∠ECB=180°,
( )∥( ),( )
∴∠ABC=∠BCD.( )
∵∠P=∠Q,
∴PB∥CQ,( ).
∴( ).(两直线平行,内错角相等)
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
25.如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:(1)BD∥CE;
(2)∠A=∠F.
26.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,试问∠2与∠3的大小关系?说明理由.
27.△ABC中,BD⊥AC于点D,点G是边AB上一点,且∠AGD=∠ABC,点E是直线BC上一点,过点E作EF⊥AC交直线AC于点F.
(1)如图,若点E是边BC延长线上一点,
①当∠DBC=36°时,求∠BEF的度数;
②判断∠BDG与∠BEF的关系,并说明理由;
(2)若点E是射线CB上一点,请直接写出∠BDG与∠BEF的关系.
28.如图,点H、点D在AB上,点F、点G在AC上,点E在BC上,已知HG⊥AB,DF⊥AB,∠2+∠3=180°,求证:∠1=∠A.
证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG( ).
∴∠3+ =180°( ).
∵∠2+∠3=180°(已知),
∴∠2=∠4( ).
∴ (内错角相等,两直线平行).
∴∠1=∠A( ).
参考答案
1.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
2.证明:∵AB⊥BF,
∴∠B=90°(垂线的定义).
∵∠CDF=90°,
∴∠B=∠CDF,
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠2,
∴AB∥EF(内错角相等,两直线平行),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠3=∠E(两直线平行,同位角相等).
故答案为:90°;垂线的定义;同位角相等,两直线平行;EF;内错角相等,两直线平行;EF;平行于同一直线的两条直线平行;两直线平行,同位角相等.
3.解:c∥d,理由如下:
∵a∥b,
∴∠2=∠3,
∵∠3=∠4,
∴∠4=∠2,
∴c∥d.
4.解:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°(垂直定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠E(两直线平行,同位角相等),
∠2=∠3(两直线平行,内错角相等),
∵∠3=∠E(已知),
∴∠1=∠2(等量代换),
∴AD平分∠BAC(角平分线定义),
故答案为:∠EGC;AD;∠E;两直线平行,同位角角相等;两直线平行,内错角相等;∠1;等量代换;角平分线的定义.
5.解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB=∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
6.解:∵DE∥BC,
∴∠DEB=∠EBC(两直线平行,内错角相等),
∵∠DEB=∠GFC,
∴∠1=∠GFC(等量代换),
∴BE∥FG(同位角相等,两直线平行).
故答案为:∠EBC;两直线平行,内错角相等;∠EBC;等量代换;同位角相等,两直线平行.
7.解:∵∠1=∠2(已知),
又∵∠2=∠BAC(对顶角相等),
∴∠BAC=∠1(等量代换),
∴AC∥BE(同位角相等,两直线平行),
∴∠C=∠4(两直线平行,同位角相等),
∵∠C=∠5(已知),
∴∠4=∠5,(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:对顶角相等;AC;BE;同位角相等,两直线平行;两直线平行,同位角相等;4;5;内错角相等,两直线平行.
8.(1)证明:∵∠1=50°,∠2=130°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)解:∠A=∠F,理由如下:
∵BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
9.证明:(1)∵∠A=∠AGE,∠D=∠DGC,∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD;
(2)∵∠1=∠BHG,∠1+∠2=180°,
∴∠2+∠BHG=180°,
∴BF∥CE,
∴∠BEC+∠B=180°.
10.证明:∵∠1+∠DFE=180°,∠1+∠2=180°,
∴∠2=∠DFE,
∴BD∥EF,
∴∠3+∠BDE=180°,
又∵∠3=∠B,
∴∠B+∠BDE=180°,
∴DE∥BC,
∴∠AED=∠ACB.
11.解:(1)EF和AB的位置关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=68°,
∴∠ECD=112°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=42°.
12.证明:∵∠1+∠2=180(已知),
∠2+∠CDB=180°(邻补角的定义),
∴∠CDB=∠1(等角的补角相等),
∴DC∥AE(同位角相等,两直线平行),
∴∠C=∠CBE(两直线平行,内错角相等),
∵∠A=∠C(已知),
∴∠A=∠CBE(等量代换),
∴AD∥BC(同位角相等,两直线平行).
故答案为:∠1;AE;同位角相等,两直线平行;∠CBE;两直线平行,内错角相等;∠CBE;等量代换;同位角相等,两直线平行.
13.证明:∵∠1+∠2=180°(已知),
∠2=∠4(对顶角相等),
∴∠1+∠4=180°(等量代换),
∴AB∥DF(同旁内角互补,两直线平行),
∴∠B=∠FDH(两直线平行,同位角相等),
∵∠3=∠B(已知),
∴∠3=∠FDH(等量代换),
∴EF∥BC(内错角相等,两直线平行).
故答案为:对顶角相等;DF;同旁内角互补,两直线平行;∠FDH;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
14.解:(1)DE∥BC,理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DE∥BC;
(2)∵∠B=40°,∠ACB﹣10°=∠A,
∴∠ACB+(∠ACB﹣10°)+40°=180°,
∴∠ACB=75°,
由(1)知,DE∥BC,
∴∠DEC+∠ACB=180°,
∴∠DEC=105°.
15.解:∠A和∠D的数量关系是相等.
理由是:如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴BF∥CE,
∴∠ABF=∠C,
∵∠C=∠F,
∴∠ABF=∠F,
∴AC∥DF,
∴∠A=∠D.
16.解:(1)BD∥FG的理由如下:
∵AB⊥BC,DE⊥AB,
∴DE∥BC.
∴∠1=∠DBC.
∵∠1=∠2,
∴∠DBC=∠2.
∴BD∥FG.
(2)在Rt△ABC中,∵AB=4,BC=3,
∴AC==5.
∵D是AC的中点,
∴BD=AC=.
∵F是BC的中点,BD∥FG,
∴FG是△CBD的中位线.
∴FG=BD=.
17.(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
18.解:∵∠A=∠C,
∴AB∥CD,
∴∠B=∠CFH,
∵∠B=∠D,
∴∠CFH=∠D,
∴BH∥ED,
∴∠1=∠DGH=62°,
∴∠2=180°﹣∠1=118°.
19.证明:∵AB⊥BF,CD⊥BF,
∴AB∥CD,
∵∠BAF=∠AFE,
∴AB∥EF,
∴CD∥EF,
∴∠ACD=∠E.
20.证明:∵∠E=∠2(已知),
∴BE∥DF(内错角相等,两直线平行),
∴∠CDF=∠1(两直线平行,同位角相等).
又∵AB∥CD(已知),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=∠CDF(等量代换).
∵DE平分∠CDF(已知),
∴∠CDF=2∠2(角平分线的定义).
∴∠B=2∠2(等量代换).
故答案为:内错角相等,两直线平行;1;1;两直线平行,同位角相等;2;等量代换.
21.解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(垂直的定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠BEF=∠BAD(两直线平行,同位角相等),
∵∠BEF=∠ADG(已知),
∴∠ADG=∠BAD(等量代换),
∴DG∥AB(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;∠BAD;∠ADG=∠BAD;内错角相等,两直线平行.
22.解:∵∠DHF=∠AHB( 对顶角相等),
∠DHF=∠AGE(已知),
∴∠AHB=∠AGE( 等量代换),
∴BH∥EC( 同位角相等,两直线平行),
∴∠B=∠AEG(两直线平行,同位角相等).
∵∠B=∠C(已知),
∴∠AEG=∠C.
∴AB∥CD( 内错角相等,两直线平行).
∴∠A=∠D( 两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;EC;同位角相等,两直线平行;∠AEG;∠AEG;CD;内错角相等,两直线平行;两直线平行,内错角相等.
23.解:(1)AB∥CD.
证明:∵BE,DE平分∠ABD,∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD.(同旁内角互补,两直线平行);
(2)解:∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°,
∴∠3+∠FDE=90°,
∴∠2+∠3=90°,
∵∠2=36°,
∴∠3=54°.
24.证明:∵∠ABC+∠ECB=180°,
∴(AB)∥(ED),(同旁内角互补,两直线平行)
∴∠ABC=∠BCD,(两直线平行,内错角相等)
∵∠P=∠Q,
∴PB∥CQ,(内错角相等,两直线平行)
∴∠PBC=∠BCQ,(两直线平行,内错角相等)
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
故答案为:AB,ED,同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;∠PBC=∠BCQ.
25.证明:(1)∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE.(同位角相等,两直线平行);
(2)∵BD∥CE,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠DBA=∠D,
∴DF∥AC,(内错角相等,两直线平行),
∴∠A=∠F.(两直线平行,内错角相等).
26.解:∠2=∠3.理由如下:
∵AD⊥BC于D,EG⊥BC于G,
∴AD∥BC,
∴∠E=∠3,∠1=∠2,
∵∠E=∠1,
∴∠2=∠3.
27.解:(1)①∵BD⊥AC,EF⊥AC,点E是直线BC上一点,点F在直线AC上,
∴∠BDC=∠CFE=90°
∴BD∥EF,
∴∠BEF=∠DBC,
∵∠DBC=36°,
∴∠BEF=∠DBC=36°;
②∠BDG=∠BEF,
理由:∵∠AGD=∠ABC,
∴DG∥BC,
∴∠BDG=∠DBC,
∵BD∥EF,
∴∠BDG=∠BEF;
(2)∠BDG=∠BEF,
理由:如图所示:
∵BD⊥AC,EF⊥AC,点E是射线CB上一点,点F在直线AC上,
∴∠BDC=∠CFE=90°
∴BD∥EF,
∴∠BEF=∠DBC,
∵∠AGD=∠ABC,
∴DG∥BC,
∴∠BDG=∠DBC,
∴∠BDG=∠BEF.
28.证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG(同位角相等,两直线平行),
∴∠3+∠4=180°(两直线平行,同旁内角互补),
∵∠2+∠3=180°(已知),
∴∠2=∠4(等量代换),
∴DE∥AC(内错角相等,两直线平行).
∴∠1=∠A(两直线平行,同位角相等).
故答案为:同位角相等,两直线平行;∠4,两直线平行,同旁内角互补;等量代换;DE∥AC;两直线平行,同位角相等.
1.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
2.完成下面的证明:
如图所示,AB⊥BF,∠CDF=90°,∠1=∠2,求证:∠3=∠E.
证明:∵AB⊥BF,
∴∠B= ( ).
∵∠CDF=90,
∴∠B=∠CDF,
∴AB∥CD( ).
∵∠1=∠2,
∴AB∥ ( ),
∴CD∥ ( ),
∴∠3=∠E( ).
3.如图,已知a∥b,∠3=∠4,那么直线c与直线d平行吗?请说明理由.
4.完成下面推理过程,并在括号中填写推理依据:
如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,试说明:AD平分∠BAC.
证明:∵AD⊥BC,EG⊥BC
∴∠ADC= =90°(垂直定义)
∴ ∥EG(同位角相等,两直线平行)
∴∠1= ( )
∠2=∠3( )
又∵∠3=∠E(已知)
∴ =∠2( )
∴AD平分∠BAC ( )
5.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
6.按要求完成下列证明:
已知:如图,DE∥BC,∠DEB=∠GFC.求证BE∥FG.
证明:∵DE∥BC;
∴∠DEB= ( ).
∵∠DEB=∠GFC.
∴ =∠GFC( ).
∴BE∥FG( ).
7.如图,已知∠C=∠5,∠1=∠2,那么AB∥CD,为什么?
请完成下列推理过程:
∵∠1=∠2(已知)
又∵∠2=∠BAC( )
∴∠BAC=∠1(等量代换)
∴ ∥ ( )
∴∠C=∠4( )
∵∠C=∠5(已知)
∴∠ =∠ ,(等量代换)
∴AB∥CD( )
8.如图,∠1=50°,∠2=130°,∠C=∠D.
(1)试说明:BD∥CE.
(2)探索∠A与∠F的数量关系,并说明理由.
9.如图,已知∠A=∠AGE,∠D=∠DGC.
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°.
10.如图在三角形ABC中,已知∠1+∠2=180°,∠3=∠B.
求证:∠AED=∠C.
11.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.
(1)直线EF与AB有怎样的位置关系?说明理由;
(2)若∠CEF=68°,则∠ACB的度数是多少?
12.完成下面的证明:
如图,已知∠1+∠2=180,∠A=∠C.求证:AD∥BC.
证明:∵∠1+∠2=180(已知),
∠2+∠CDB=180°(邻补角的定义),
∴∠CDB= (等角的补角相等).
∴DC∥ ( ).
∴∠C= ( ).
∵∠A=∠C(已知),
∴∠A= ( ).
∴AD∥BC( ).
13.如图,∠1+∠2=180°,∠3=∠B.求证:EF∥BC,请完成证明过程及理由填写.
证明:∵∠1+∠2=180°(已知),
∠2=∠4( ).
∴∠1+∠4=180°(等量代换).
∴AB∥ ( ).
∴∠B= ( ).
∵∠3=∠B ( ),
∴∠3=∠FDH ( ).
∴EF∥BC ( ).
14.已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.
(1)那么DE与BC平行吗?为什么?
(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.
15.如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.
16.如图,已知AB⊥BC,DE⊥AB,∠1=∠2.
(1)请说明BD∥FG的理由.
(2)若D是AC的中点,F是BC的中点,已知AB=4,BC=3,求FG的长度.
17.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
18.如图,点E、F分别是AB、CD上的点,AC交DE、BF于点G、H,∠A=∠C,∠B=∠D.若∠1=62°,求∠2的度数.
19.如图,已知AB⊥BF,CD⊥BF,垂足分别为点B,D,∠BAF=∠AFE.求证:∠ACD=∠E.
20.完成下面的证明:
已知:如图,AB∥CD,CD和BE相交于点O,DE平分∠CDF,DE和BE相交于点E,∠E=∠2.
求证:∠B=2∠2.
证明:∵∠E=∠2(已知),
∴BE∥DF( ),
∴∠CDF=∠ (两直线平行,同位角相等).
又∵AB∥CD(已知),
∴∠B=∠ ( ),
∴∠B=∠CDF(等量代换).
∵DE平分∠CDF(已知),
∴∠CDF=2∠ (角平分线的定义).
∴∠B=2∠2( ).
21.如图所示,AD⊥BC,EF⊥BC,∠BEF=∠ADG.试说明DG∥AB.把说明的过程填写完整.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°( ),
∴EF∥AD( ),
∴∠BEF= ( 两直线平行,同位角相等 ).
∵∠BEF=∠ADG(已知),
∴ (等量代换).
∴DG∥AB( ).
22.如图,点E、F分别是直线AB、CD上的点,分别连接AD、EC,交点为G,连接BF,与AD交于点H,若已知∠DHF=∠AGE,∠B=∠C试证明:∠A=∠D.
请根据题意将下面的解答过程补充完整:
解:∵∠DHF=∠AHB( ),
∠DHF=∠AGE(已知),
∴∠AHB=∠AGE( ),
∴BH∥ ( ),
∴∠B= (两直线平行,同位角相等).
∵∠B=∠C(已知),
∴ =∠C.
∴AB∥ ( ).
∴∠A=∠D( ).
23.如图所示,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°
(1)试判断AB与CD的位置关系,并说明理由;
(2)若∠2=36°,求∠3的度数.
24.完成下列证明:如图,已知∠ABC+∠ECB=180°,∠P=∠Q.
求证:∠1=∠2.
证明:∵∠ABC+∠ECB=180°,
( )∥( ),( )
∴∠ABC=∠BCD.( )
∵∠P=∠Q,
∴PB∥CQ,( ).
∴( ).(两直线平行,内错角相等)
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
25.如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:(1)BD∥CE;
(2)∠A=∠F.
26.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,试问∠2与∠3的大小关系?说明理由.
27.△ABC中,BD⊥AC于点D,点G是边AB上一点,且∠AGD=∠ABC,点E是直线BC上一点,过点E作EF⊥AC交直线AC于点F.
(1)如图,若点E是边BC延长线上一点,
①当∠DBC=36°时,求∠BEF的度数;
②判断∠BDG与∠BEF的关系,并说明理由;
(2)若点E是射线CB上一点,请直接写出∠BDG与∠BEF的关系.
28.如图,点H、点D在AB上,点F、点G在AC上,点E在BC上,已知HG⊥AB,DF⊥AB,∠2+∠3=180°,求证:∠1=∠A.
证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG( ).
∴∠3+ =180°( ).
∵∠2+∠3=180°(已知),
∴∠2=∠4( ).
∴ (内错角相等,两直线平行).
∴∠1=∠A( ).
参考答案
1.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
2.证明:∵AB⊥BF,
∴∠B=90°(垂线的定义).
∵∠CDF=90°,
∴∠B=∠CDF,
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠2,
∴AB∥EF(内错角相等,两直线平行),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠3=∠E(两直线平行,同位角相等).
故答案为:90°;垂线的定义;同位角相等,两直线平行;EF;内错角相等,两直线平行;EF;平行于同一直线的两条直线平行;两直线平行,同位角相等.
3.解:c∥d,理由如下:
∵a∥b,
∴∠2=∠3,
∵∠3=∠4,
∴∠4=∠2,
∴c∥d.
4.解:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°(垂直定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠E(两直线平行,同位角相等),
∠2=∠3(两直线平行,内错角相等),
∵∠3=∠E(已知),
∴∠1=∠2(等量代换),
∴AD平分∠BAC(角平分线定义),
故答案为:∠EGC;AD;∠E;两直线平行,同位角角相等;两直线平行,内错角相等;∠1;等量代换;角平分线的定义.
5.解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB=∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
6.解:∵DE∥BC,
∴∠DEB=∠EBC(两直线平行,内错角相等),
∵∠DEB=∠GFC,
∴∠1=∠GFC(等量代换),
∴BE∥FG(同位角相等,两直线平行).
故答案为:∠EBC;两直线平行,内错角相等;∠EBC;等量代换;同位角相等,两直线平行.
7.解:∵∠1=∠2(已知),
又∵∠2=∠BAC(对顶角相等),
∴∠BAC=∠1(等量代换),
∴AC∥BE(同位角相等,两直线平行),
∴∠C=∠4(两直线平行,同位角相等),
∵∠C=∠5(已知),
∴∠4=∠5,(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:对顶角相等;AC;BE;同位角相等,两直线平行;两直线平行,同位角相等;4;5;内错角相等,两直线平行.
8.(1)证明:∵∠1=50°,∠2=130°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)解:∠A=∠F,理由如下:
∵BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
9.证明:(1)∵∠A=∠AGE,∠D=∠DGC,∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD;
(2)∵∠1=∠BHG,∠1+∠2=180°,
∴∠2+∠BHG=180°,
∴BF∥CE,
∴∠BEC+∠B=180°.
10.证明:∵∠1+∠DFE=180°,∠1+∠2=180°,
∴∠2=∠DFE,
∴BD∥EF,
∴∠3+∠BDE=180°,
又∵∠3=∠B,
∴∠B+∠BDE=180°,
∴DE∥BC,
∴∠AED=∠ACB.
11.解:(1)EF和AB的位置关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=68°,
∴∠ECD=112°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=42°.
12.证明:∵∠1+∠2=180(已知),
∠2+∠CDB=180°(邻补角的定义),
∴∠CDB=∠1(等角的补角相等),
∴DC∥AE(同位角相等,两直线平行),
∴∠C=∠CBE(两直线平行,内错角相等),
∵∠A=∠C(已知),
∴∠A=∠CBE(等量代换),
∴AD∥BC(同位角相等,两直线平行).
故答案为:∠1;AE;同位角相等,两直线平行;∠CBE;两直线平行,内错角相等;∠CBE;等量代换;同位角相等,两直线平行.
13.证明:∵∠1+∠2=180°(已知),
∠2=∠4(对顶角相等),
∴∠1+∠4=180°(等量代换),
∴AB∥DF(同旁内角互补,两直线平行),
∴∠B=∠FDH(两直线平行,同位角相等),
∵∠3=∠B(已知),
∴∠3=∠FDH(等量代换),
∴EF∥BC(内错角相等,两直线平行).
故答案为:对顶角相等;DF;同旁内角互补,两直线平行;∠FDH;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
14.解:(1)DE∥BC,理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DE∥BC;
(2)∵∠B=40°,∠ACB﹣10°=∠A,
∴∠ACB+(∠ACB﹣10°)+40°=180°,
∴∠ACB=75°,
由(1)知,DE∥BC,
∴∠DEC+∠ACB=180°,
∴∠DEC=105°.
15.解:∠A和∠D的数量关系是相等.
理由是:如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴BF∥CE,
∴∠ABF=∠C,
∵∠C=∠F,
∴∠ABF=∠F,
∴AC∥DF,
∴∠A=∠D.
16.解:(1)BD∥FG的理由如下:
∵AB⊥BC,DE⊥AB,
∴DE∥BC.
∴∠1=∠DBC.
∵∠1=∠2,
∴∠DBC=∠2.
∴BD∥FG.
(2)在Rt△ABC中,∵AB=4,BC=3,
∴AC==5.
∵D是AC的中点,
∴BD=AC=.
∵F是BC的中点,BD∥FG,
∴FG是△CBD的中位线.
∴FG=BD=.
17.(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
18.解:∵∠A=∠C,
∴AB∥CD,
∴∠B=∠CFH,
∵∠B=∠D,
∴∠CFH=∠D,
∴BH∥ED,
∴∠1=∠DGH=62°,
∴∠2=180°﹣∠1=118°.
19.证明:∵AB⊥BF,CD⊥BF,
∴AB∥CD,
∵∠BAF=∠AFE,
∴AB∥EF,
∴CD∥EF,
∴∠ACD=∠E.
20.证明:∵∠E=∠2(已知),
∴BE∥DF(内错角相等,两直线平行),
∴∠CDF=∠1(两直线平行,同位角相等).
又∵AB∥CD(已知),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=∠CDF(等量代换).
∵DE平分∠CDF(已知),
∴∠CDF=2∠2(角平分线的定义).
∴∠B=2∠2(等量代换).
故答案为:内错角相等,两直线平行;1;1;两直线平行,同位角相等;2;等量代换.
21.解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=∠ADB=90°(垂直的定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠BEF=∠BAD(两直线平行,同位角相等),
∵∠BEF=∠ADG(已知),
∴∠ADG=∠BAD(等量代换),
∴DG∥AB(内错角相等,两直线平行).
故答案为:垂直的定义;同位角相等,两直线平行;∠BAD;∠ADG=∠BAD;内错角相等,两直线平行.
22.解:∵∠DHF=∠AHB( 对顶角相等),
∠DHF=∠AGE(已知),
∴∠AHB=∠AGE( 等量代换),
∴BH∥EC( 同位角相等,两直线平行),
∴∠B=∠AEG(两直线平行,同位角相等).
∵∠B=∠C(已知),
∴∠AEG=∠C.
∴AB∥CD( 内错角相等,两直线平行).
∴∠A=∠D( 两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;EC;同位角相等,两直线平行;∠AEG;∠AEG;CD;内错角相等,两直线平行;两直线平行,内错角相等.
23.解:(1)AB∥CD.
证明:∵BE,DE平分∠ABD,∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD.(同旁内角互补,两直线平行);
(2)解:∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°,
∴∠3+∠FDE=90°,
∴∠2+∠3=90°,
∵∠2=36°,
∴∠3=54°.
24.证明:∵∠ABC+∠ECB=180°,
∴(AB)∥(ED),(同旁内角互补,两直线平行)
∴∠ABC=∠BCD,(两直线平行,内错角相等)
∵∠P=∠Q,
∴PB∥CQ,(内错角相等,两直线平行)
∴∠PBC=∠BCQ,(两直线平行,内错角相等)
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
故答案为:AB,ED,同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;∠PBC=∠BCQ.
25.证明:(1)∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE.(同位角相等,两直线平行);
(2)∵BD∥CE,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠DBA=∠D,
∴DF∥AC,(内错角相等,两直线平行),
∴∠A=∠F.(两直线平行,内错角相等).
26.解:∠2=∠3.理由如下:
∵AD⊥BC于D,EG⊥BC于G,
∴AD∥BC,
∴∠E=∠3,∠1=∠2,
∵∠E=∠1,
∴∠2=∠3.
27.解:(1)①∵BD⊥AC,EF⊥AC,点E是直线BC上一点,点F在直线AC上,
∴∠BDC=∠CFE=90°
∴BD∥EF,
∴∠BEF=∠DBC,
∵∠DBC=36°,
∴∠BEF=∠DBC=36°;
②∠BDG=∠BEF,
理由:∵∠AGD=∠ABC,
∴DG∥BC,
∴∠BDG=∠DBC,
∵BD∥EF,
∴∠BDG=∠BEF;
(2)∠BDG=∠BEF,
理由:如图所示:
∵BD⊥AC,EF⊥AC,点E是射线CB上一点,点F在直线AC上,
∴∠BDC=∠CFE=90°
∴BD∥EF,
∴∠BEF=∠DBC,
∵∠AGD=∠ABC,
∴DG∥BC,
∴∠BDG=∠DBC,
∴∠BDG=∠BEF.
28.证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG(同位角相等,两直线平行),
∴∠3+∠4=180°(两直线平行,同旁内角互补),
∵∠2+∠3=180°(已知),
∴∠2=∠4(等量代换),
∴DE∥AC(内错角相等,两直线平行).
∴∠1=∠A(两直线平行,同位角相等).
故答案为:同位角相等,两直线平行;∠4,两直线平行,同旁内角互补;等量代换;DE∥AC;两直线平行,同位角相等.
