20.1数据的集中趋势(1)同步练习(含解析)人教版数学八年级下册
文档属性
| 名称 | 20.1数据的集中趋势(1)同步练习(含解析)人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 159.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 20:24:20 | ||
图片预览



文档简介
人教版八年级下第二十章数据的分析20.1数据的集中趋势
一、单选题
1.在中国共产主义青年团成立100周年之际,某校团委招募志愿者到六个社区开展“书香成都”全民阅读服务活动,报名人数分别为:56,60,63,60,60,72,则这组数据的众数和中位数分别是( )
A.56,60 B.60,72 C.60,63 D.60,60
2.宿州学院排球队有12名队员,队员的年龄情况如图所示,那么球队队员年龄的众数、中位数分别是( )
A.19,19 B.19,20 C.20,20 D.22,19
3.为了解美食节同学们最喜爱的菜肴,需要获取的统计量是( )
A.平均数 B.中位数 C.众数 D.
4.已知一组数据,前8个数据的平均数是x,还有两个数据的分别为84,84,则这组数据的平均数是( )
A. B. C. D.
5.李华参加演讲比赛,有九位评委打分,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
6.下列说法正确的是( )
A.数据3,3,4,4,7的众数是4
B.数据0,1,2,5,1的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,,,7的中位数和平均数都是0
7. 双减政策落地,各地学校大力提升学生核心素养,学生的综合评价分学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价,若宸宸学习成绩为900分,体育成绩为80分,艺术成绩为85分,则他的综合评价得分为( )
A.84 B.85 C.86 D.87
8.一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )
A.方差 B.平均数 C.中位数 D.众数
9.若一组数据 , , 的平均数为4,方差为3,那么数据 , , 的平均数和方差分别是( )
A.4, 3 B.6 3 C.3 4 D.6 5
10.某一公司共有51名员工(其中包括1名经理),经理的工资高于其他员工的工资,今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会( )
A.平均数增加,中位数不变 B.平均数和中位数不变
C.平均数不变,中位数增加 D.平均数和中位数均增加
二、填空题
11.如果一组数据由四个整数组成,其中三个分别是2,4,6,且这组数据的中位数也是整数,那么这组数据的中位数是 .
12.某校运动会入场式的得分是由各班入场时,评委从服装统一,动作整齐和口号响亮这三项分别给分,最后按3:3:4的比例计算所得.若801班在服装、动作、口号方面的评分分别是90分,92分,86分,则该班的入场式的得分是 分.
13.若一组数据2,3,x,5,6的平均数为5,则x= .
14.已知数据x1,x2 ,…,xn的平均数是2,方差是3,则一组新数据2x1+4,2x2+4,…,2xn+4的平均数是 ,方差是 .
15.在校园歌手大奖赛上,比赛规则是:七位评委打分,去掉一个最高分和一个最低分后,所剩数据取平均数即为选手的最后得分.七位评委给某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,则这位歌手的最后得分是 .
16.为迎接体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是13,平均数是12,那么这组数据的方差是 。
三、解答题
17.2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,学校举办科技知识竞赛活动,竞赛内容分“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目,下表是小亮和小明的各项成绩:(百分制)
航天技术 生物技术 能源技术 其它技术领域
小亮 85 90 95 90
小明 100 90 80 90
若“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目按确定综合成绩,则小亮和小明谁的综合成绩高?请通过计算说明理由.
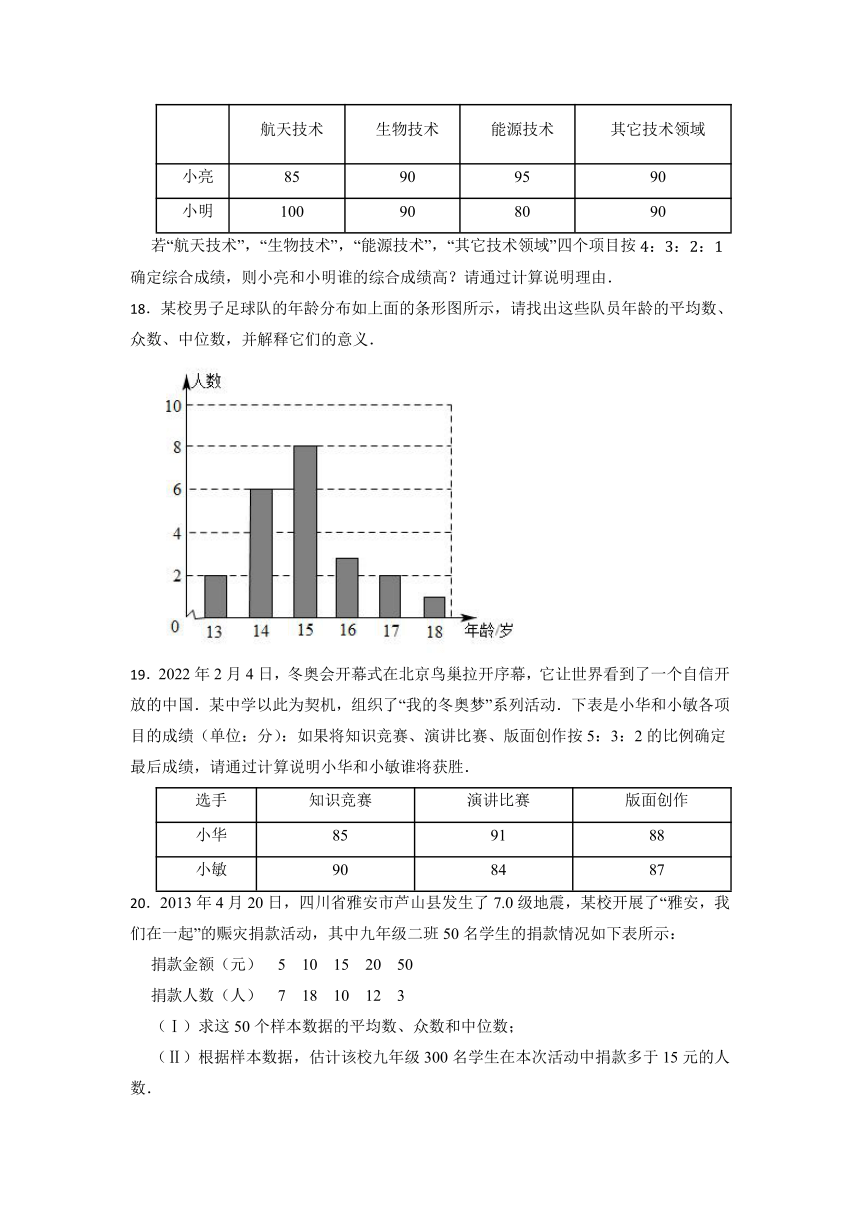
18.某校男子足球队的年龄分布如上面的条形图所示,请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
19.2022年2月4日,冬奥会开幕式在北京鸟巢拉开序幕,它让世界看到了一个自信开放的中国.某中学以此为契机,组织了“我的冬奥梦”系列活动.下表是小华和小敏各项目的成绩(单位:分):如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明小华和小敏谁将获胜.
选手 知识竞赛 演讲比赛 版面创作
小华 85 91 88
小敏 90 84 87
20.2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
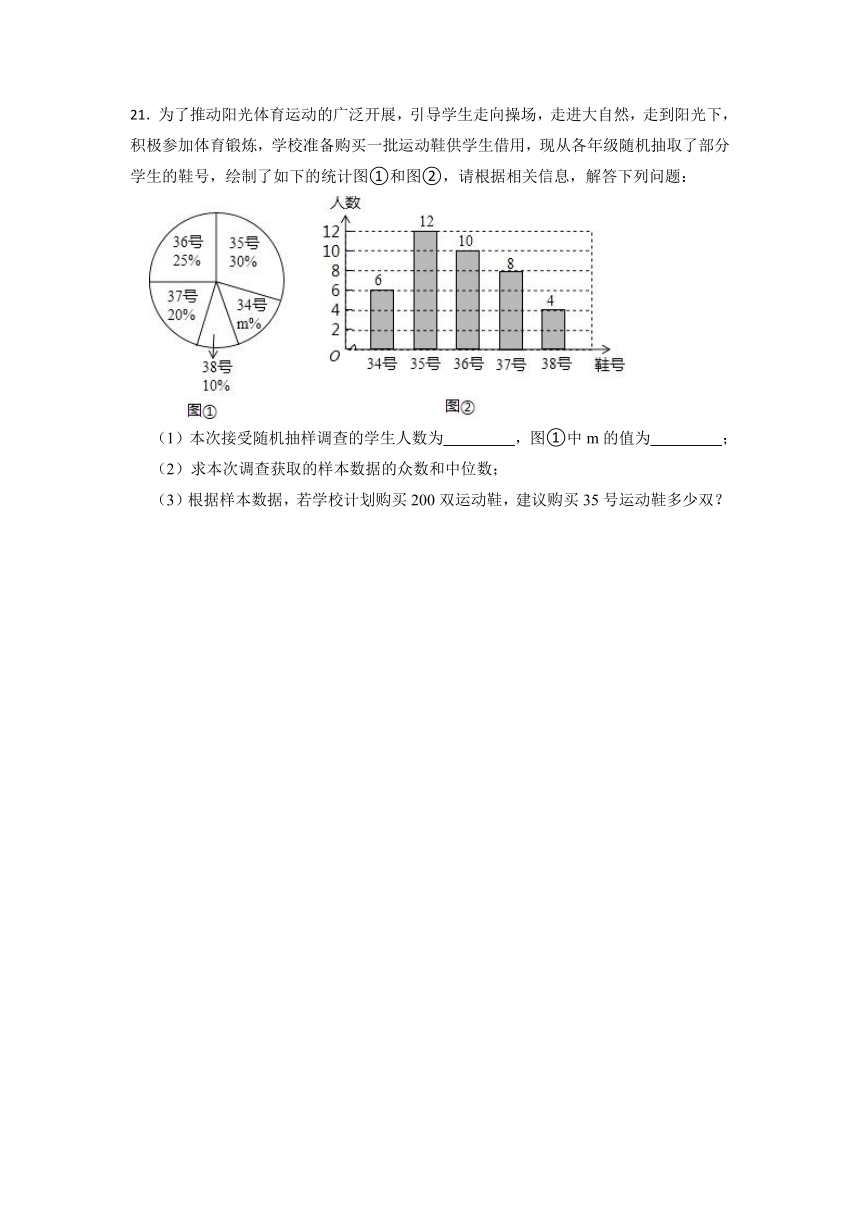
21.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
答案解析部分
1.【答案】D
【解析】【解答】解:将这组数据按从小到大排列为:56、60、60、60、63、72,
这组数据中出现次数最多的数据是60,故这组数据的众数是60,
这组数据共6个,排第3与第4位的数据都是60,所以中位数是60.
故答案为:D.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此并结合题意,即可得出答案.
2.【答案】A
【解析】【解答】解:由条形统计图可知,年龄是19岁的人最多,有5人,故这组数据的众数为19;
将12名队员的年龄按从小到大排列后排第6与第7位的都是19,所以这组数据的中位数是19.
故答案为:A.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此并结合条形统计图提供的信息,即可得出答案.
3.【答案】C
【解析】【解答】解:要了解同学们最喜爱的菜肴,
就是了解哪个菜肴喜欢的人数最多,即为众数,
故答案为:C.
【分析】众数是指一组数据中出现次数最多的数,且不受极端数据的影响,所以要了解同学们最喜爱的菜肴,只需了解众数即可.
4.【答案】D
【解析】【解答】解:这组数据的平均数为:.
故答案为:D.
【分析】根据平均数的定义可得前8个数的和为8x,进而根据平均数=数据的总和除以数据的个数列式计算即可.
5.【答案】B
【解析】【解答】解:去掉一个最高分和一个最低分,平均分、众数、方差可能发生变化,中位数一定不发生变化,
故答案为:B.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,平均数是一组数据的总和除以这组数据的总个数,方差是一组数据中各个数据与这组数据的平均数差的平方和的算术平均数,据此一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、数据3,3,4,4,7的众数是4和3,故A不符合题意;
B、数据0,1,2,5,1的中位数是1,故B不符合题意;
C、一组数据的众数和中位数可能相等,故C不符合题意;
D、数据0,5,-7,-5,7
排序为-7,-5,0,5,7,
中位数为0,
平均数为
∴这组数据的中位数和平均数都是0,故D符合题意;
故答案为:D
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,利用平均数公式,可求出D选项中的数据的平均数,据此可对各选项逐一判断.
7.【答案】C
【解析】【解答】解:根据题意,他的综合评价得分为(分).
故他的总成绩是86分.
故答案为:C.
【分析】利用学习成绩×5+体育成绩×3+艺术成绩×2,然后再除以(5+3+2)就可求出综合评价得分.
8.【答案】D
【解析】【解答】解:加入一个数a,观察可得:2出现了3次,且出现的次数最多,故众数不会发生变化.
故答案为:D.
【分析】众数是出现次数最多的数据,观察可得2出现的次数最多,据此判断.
9.【答案】B
【解析】【解答】解:∵数据a1,a2,a3的平均数为4,
∴ (a1+a2+a3)=4,
∴ (a1+2+a2+2+a3+2)= (a1+a2+a3)+2=4+2=6,
∴数据a1+2,a2+2,a3+2的平均数是6;
∵数据a1,a2,a3的方差为3,
∴ [(a1-4)2+(a2-4)2+(a3-4)2]=3,
∴a1+2,a2+2,a3+2的方差为: [(a1+2-6)2+(a2+2-6)2+(a3+2-6)2]
= [(a1-4)2+(a2-4)2+(a3-4)2]
=3.
故答案为:B.
【分析】根据数据a1,a2,a3的平均数为4可知 (a1+a2+a3)=4,据此可得出 (a1+2+a2+2+a3+2)的值;再由方差为3可得出数据a1+2,a2+2,a3+2的方差
10.【答案】A
【解析】【解答】设这家公司除经理外50名员工的工资和为a元,则这家公司所有员工去年工资的平均数是元,今年工资的平均数是元,显然<;
由于这51个数据按从小到大的顺序排列的次序完全没有变化,所以中位数不变.
故选A.
【分析】本题考查统计的有关知识,找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,平均数是指在一组数据中所有数据之和再除以数据的个数.本题主要考查了平均数,中位数的概念,要掌握这些基本概念才能熟练解题.同时注意到个别数据对平均数的影响较大,而对中位数和众数没影响.
11.【答案】3或4或5
【解析】【解答】解:①当第四个整数小于或等于2时,中位数为:(2+4)÷2=3,满足题意;
②当第四个整数大于2且小于4时,此时第四个整数是3,中位数为:(3+4)÷2=3.5,中位数不是整数,不满足题意;
③当第四个整数等于4时,中位数是: (4+4)÷ 2=4,满足题意;
④当第四个整数大于4且小于6时,只有5这一个整数,而中位数不是整数,不满足题意;
⑤当第四个整数大于或等于6时,中位数是:(4 +6)÷2=5,满足题意,
所以它们的中位数是3或4或5.
故答案为:3或4或5.
【分析】找中位数的时候一定要先排好顺序,然后再根据奇数或偶数个数来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个,则找中间两位数的平均数;第四个整数可能情况有:小于或等于2;大于2且小于4;等于4;大于4且小于6;大于6,分几种情况进行求解即可.
12.【答案】89
【解析】【解答】解:该班的入场式的得分是 =89(分).
故答案为:89.
【分析】利用服装统一得分×3+动作整齐得分×3+口号响亮得分×4,然后除以(3+3+4)即可求出得分.
13.【答案】9
【解析】【解答】解:∵数据2,3,x,5,6的平均数为5,
∴=5,
解得x=9,
故答案为:9.
【分析】根据数据之和÷数据的个数=平均数进行计算.
14.【答案】8;12
【解析】【解答】解:∵ 数据x1,x2 ,…,xn的平均数是2,
∴,
∴;
∵ 数据x1,x2 ,…,xn的方差是3,
∴2x1+4,2x2+4,…,2xn+4的方差是3×22=12.
故答案为:8,12
【分析】利用平均数公式可得到,据此可求出新数据2x1+4,2x2+4,…,2xn+4的平均数和方差.
15.【答案】9.5
【解析】【解答】根据题意,去掉9.9和9.0两个分数,
剩下5个数的平均数为:,
故答案为:9.5.
【分析】利用平均数的计算方法求解即可。
16.【答案】
【解析】【解答】解:∵平均数为12,
∴这组数据的和=12×7=84,
所以被墨汁覆盖的数的和=84-11-12-13-12=36,
又∵这组数据的众数为13,
∴被覆盖的三个数为:10,13,13,
所以这组数据的方差s2=
=.
故答案为:.
【分析】根据已知条件可推出被墨汁覆盖的三个数是10,13,13,再根据方差公式进行计算即可.
17.【答案】解:小亮分
小明分
∵
∴小明的体能综合成绩高.
【解析】【分析】根据航天技术得分×4+生物技术得分×3+能源技术得分×2+其它技术领域得分×1,然后除以10求出小亮、小明的平均分,然后进行比较即可判断.
18.【答案】解:平均数为:
众数为:15,中位数为:15
故这个学校男子足球队队员的年龄的平均数是15,众数是15,中位数是15
由于平均数、众数、中位数都是15岁,故可知该校足球队的年龄数据都集中在15岁左右.
【解析】【分析】利用众数、平均数和中位数的定义及计算方法逐项判断即可。
19.【答案】解:小华的平均分为:(分),
小敏的平均分为:(分),
∵,
∴小敏将获胜.
【解析】【分析】利用加权平均数的计算方法分别求出小华和小敏的平均数,再比较大小即可。
20.【答案】解:(Ⅰ)观察表格,可知这组样本数据的平均数是 = =15.1;
∴这组样本数据的平均数是15.1
在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为10
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5
(Ⅱ)在50名学生中,捐款多于15元的学生有15名,有300× =90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
【解析】【分析】众数是一组数据中出现次数最多的数据,是一组数据中的;中位数是指一组数据从小到大排列,位于中间的那个数;可以是一个(数据为奇数),也可以是2个的平均(数据为偶数);平均数是一组数据的和,除以这组数据的个数的值,就是平均数;计算出这50个样本数据的平均数、众数和中位数;在50名学生中,捐款多于15元的学生有15名,可以估计该校九年级300名学生在本次活动中捐款多于15元的学生人数.
21.【答案】(1)40;15
(2)解:∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
(3)解:∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为6+12+10+8+4=40,图①中m的值为100﹣30﹣25﹣20﹣10=15;
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
故答案为:(1)40;15;(2)36(3)60.
【分析】(1)首先根据条形统计图求出总人数;然后由扇形统计图以及单位1,求出m的值即可;
(2)出现次数最多数据为众数,将数据按照从小到大顺序排列,中间两个数据的平均数为中位数;
(3)依据样本可知鞋号为35的学生人数比例为30%,然后依据频数=总数×百分比求解即可.
一、单选题
1.在中国共产主义青年团成立100周年之际,某校团委招募志愿者到六个社区开展“书香成都”全民阅读服务活动,报名人数分别为:56,60,63,60,60,72,则这组数据的众数和中位数分别是( )
A.56,60 B.60,72 C.60,63 D.60,60
2.宿州学院排球队有12名队员,队员的年龄情况如图所示,那么球队队员年龄的众数、中位数分别是( )
A.19,19 B.19,20 C.20,20 D.22,19
3.为了解美食节同学们最喜爱的菜肴,需要获取的统计量是( )
A.平均数 B.中位数 C.众数 D.
4.已知一组数据,前8个数据的平均数是x,还有两个数据的分别为84,84,则这组数据的平均数是( )
A. B. C. D.
5.李华参加演讲比赛,有九位评委打分,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
6.下列说法正确的是( )
A.数据3,3,4,4,7的众数是4
B.数据0,1,2,5,1的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,,,7的中位数和平均数都是0
7. 双减政策落地,各地学校大力提升学生核心素养,学生的综合评价分学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价,若宸宸学习成绩为900分,体育成绩为80分,艺术成绩为85分,则他的综合评价得分为( )
A.84 B.85 C.86 D.87
8.一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )
A.方差 B.平均数 C.中位数 D.众数
9.若一组数据 , , 的平均数为4,方差为3,那么数据 , , 的平均数和方差分别是( )
A.4, 3 B.6 3 C.3 4 D.6 5
10.某一公司共有51名员工(其中包括1名经理),经理的工资高于其他员工的工资,今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会( )
A.平均数增加,中位数不变 B.平均数和中位数不变
C.平均数不变,中位数增加 D.平均数和中位数均增加
二、填空题
11.如果一组数据由四个整数组成,其中三个分别是2,4,6,且这组数据的中位数也是整数,那么这组数据的中位数是 .
12.某校运动会入场式的得分是由各班入场时,评委从服装统一,动作整齐和口号响亮这三项分别给分,最后按3:3:4的比例计算所得.若801班在服装、动作、口号方面的评分分别是90分,92分,86分,则该班的入场式的得分是 分.
13.若一组数据2,3,x,5,6的平均数为5,则x= .
14.已知数据x1,x2 ,…,xn的平均数是2,方差是3,则一组新数据2x1+4,2x2+4,…,2xn+4的平均数是 ,方差是 .
15.在校园歌手大奖赛上,比赛规则是:七位评委打分,去掉一个最高分和一个最低分后,所剩数据取平均数即为选手的最后得分.七位评委给某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,则这位歌手的最后得分是 .
16.为迎接体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是13,平均数是12,那么这组数据的方差是 。
三、解答题
17.2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,学校举办科技知识竞赛活动,竞赛内容分“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目,下表是小亮和小明的各项成绩:(百分制)
航天技术 生物技术 能源技术 其它技术领域
小亮 85 90 95 90
小明 100 90 80 90
若“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目按确定综合成绩,则小亮和小明谁的综合成绩高?请通过计算说明理由.
18.某校男子足球队的年龄分布如上面的条形图所示,请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
19.2022年2月4日,冬奥会开幕式在北京鸟巢拉开序幕,它让世界看到了一个自信开放的中国.某中学以此为契机,组织了“我的冬奥梦”系列活动.下表是小华和小敏各项目的成绩(单位:分):如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明小华和小敏谁将获胜.
选手 知识竞赛 演讲比赛 版面创作
小华 85 91 88
小敏 90 84 87
20.2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
21.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
答案解析部分
1.【答案】D
【解析】【解答】解:将这组数据按从小到大排列为:56、60、60、60、63、72,
这组数据中出现次数最多的数据是60,故这组数据的众数是60,
这组数据共6个,排第3与第4位的数据都是60,所以中位数是60.
故答案为:D.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此并结合题意,即可得出答案.
2.【答案】A
【解析】【解答】解:由条形统计图可知,年龄是19岁的人最多,有5人,故这组数据的众数为19;
将12名队员的年龄按从小到大排列后排第6与第7位的都是19,所以这组数据的中位数是19.
故答案为:A.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此并结合条形统计图提供的信息,即可得出答案.
3.【答案】C
【解析】【解答】解:要了解同学们最喜爱的菜肴,
就是了解哪个菜肴喜欢的人数最多,即为众数,
故答案为:C.
【分析】众数是指一组数据中出现次数最多的数,且不受极端数据的影响,所以要了解同学们最喜爱的菜肴,只需了解众数即可.
4.【答案】D
【解析】【解答】解:这组数据的平均数为:.
故答案为:D.
【分析】根据平均数的定义可得前8个数的和为8x,进而根据平均数=数据的总和除以数据的个数列式计算即可.
5.【答案】B
【解析】【解答】解:去掉一个最高分和一个最低分,平均分、众数、方差可能发生变化,中位数一定不发生变化,
故答案为:B.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,平均数是一组数据的总和除以这组数据的总个数,方差是一组数据中各个数据与这组数据的平均数差的平方和的算术平均数,据此一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、数据3,3,4,4,7的众数是4和3,故A不符合题意;
B、数据0,1,2,5,1的中位数是1,故B不符合题意;
C、一组数据的众数和中位数可能相等,故C不符合题意;
D、数据0,5,-7,-5,7
排序为-7,-5,0,5,7,
中位数为0,
平均数为
∴这组数据的中位数和平均数都是0,故D符合题意;
故答案为:D
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,利用平均数公式,可求出D选项中的数据的平均数,据此可对各选项逐一判断.
7.【答案】C
【解析】【解答】解:根据题意,他的综合评价得分为(分).
故他的总成绩是86分.
故答案为:C.
【分析】利用学习成绩×5+体育成绩×3+艺术成绩×2,然后再除以(5+3+2)就可求出综合评价得分.
8.【答案】D
【解析】【解答】解:加入一个数a,观察可得:2出现了3次,且出现的次数最多,故众数不会发生变化.
故答案为:D.
【分析】众数是出现次数最多的数据,观察可得2出现的次数最多,据此判断.
9.【答案】B
【解析】【解答】解:∵数据a1,a2,a3的平均数为4,
∴ (a1+a2+a3)=4,
∴ (a1+2+a2+2+a3+2)= (a1+a2+a3)+2=4+2=6,
∴数据a1+2,a2+2,a3+2的平均数是6;
∵数据a1,a2,a3的方差为3,
∴ [(a1-4)2+(a2-4)2+(a3-4)2]=3,
∴a1+2,a2+2,a3+2的方差为: [(a1+2-6)2+(a2+2-6)2+(a3+2-6)2]
= [(a1-4)2+(a2-4)2+(a3-4)2]
=3.
故答案为:B.
【分析】根据数据a1,a2,a3的平均数为4可知 (a1+a2+a3)=4,据此可得出 (a1+2+a2+2+a3+2)的值;再由方差为3可得出数据a1+2,a2+2,a3+2的方差
10.【答案】A
【解析】【解答】设这家公司除经理外50名员工的工资和为a元,则这家公司所有员工去年工资的平均数是元,今年工资的平均数是元,显然<;
由于这51个数据按从小到大的顺序排列的次序完全没有变化,所以中位数不变.
故选A.
【分析】本题考查统计的有关知识,找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,平均数是指在一组数据中所有数据之和再除以数据的个数.本题主要考查了平均数,中位数的概念,要掌握这些基本概念才能熟练解题.同时注意到个别数据对平均数的影响较大,而对中位数和众数没影响.
11.【答案】3或4或5
【解析】【解答】解:①当第四个整数小于或等于2时,中位数为:(2+4)÷2=3,满足题意;
②当第四个整数大于2且小于4时,此时第四个整数是3,中位数为:(3+4)÷2=3.5,中位数不是整数,不满足题意;
③当第四个整数等于4时,中位数是: (4+4)÷ 2=4,满足题意;
④当第四个整数大于4且小于6时,只有5这一个整数,而中位数不是整数,不满足题意;
⑤当第四个整数大于或等于6时,中位数是:(4 +6)÷2=5,满足题意,
所以它们的中位数是3或4或5.
故答案为:3或4或5.
【分析】找中位数的时候一定要先排好顺序,然后再根据奇数或偶数个数来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个,则找中间两位数的平均数;第四个整数可能情况有:小于或等于2;大于2且小于4;等于4;大于4且小于6;大于6,分几种情况进行求解即可.
12.【答案】89
【解析】【解答】解:该班的入场式的得分是 =89(分).
故答案为:89.
【分析】利用服装统一得分×3+动作整齐得分×3+口号响亮得分×4,然后除以(3+3+4)即可求出得分.
13.【答案】9
【解析】【解答】解:∵数据2,3,x,5,6的平均数为5,
∴=5,
解得x=9,
故答案为:9.
【分析】根据数据之和÷数据的个数=平均数进行计算.
14.【答案】8;12
【解析】【解答】解:∵ 数据x1,x2 ,…,xn的平均数是2,
∴,
∴;
∵ 数据x1,x2 ,…,xn的方差是3,
∴2x1+4,2x2+4,…,2xn+4的方差是3×22=12.
故答案为:8,12
【分析】利用平均数公式可得到,据此可求出新数据2x1+4,2x2+4,…,2xn+4的平均数和方差.
15.【答案】9.5
【解析】【解答】根据题意,去掉9.9和9.0两个分数,
剩下5个数的平均数为:,
故答案为:9.5.
【分析】利用平均数的计算方法求解即可。
16.【答案】
【解析】【解答】解:∵平均数为12,
∴这组数据的和=12×7=84,
所以被墨汁覆盖的数的和=84-11-12-13-12=36,
又∵这组数据的众数为13,
∴被覆盖的三个数为:10,13,13,
所以这组数据的方差s2=
=.
故答案为:.
【分析】根据已知条件可推出被墨汁覆盖的三个数是10,13,13,再根据方差公式进行计算即可.
17.【答案】解:小亮分
小明分
∵
∴小明的体能综合成绩高.
【解析】【分析】根据航天技术得分×4+生物技术得分×3+能源技术得分×2+其它技术领域得分×1,然后除以10求出小亮、小明的平均分,然后进行比较即可判断.
18.【答案】解:平均数为:
众数为:15,中位数为:15
故这个学校男子足球队队员的年龄的平均数是15,众数是15,中位数是15
由于平均数、众数、中位数都是15岁,故可知该校足球队的年龄数据都集中在15岁左右.
【解析】【分析】利用众数、平均数和中位数的定义及计算方法逐项判断即可。
19.【答案】解:小华的平均分为:(分),
小敏的平均分为:(分),
∵,
∴小敏将获胜.
【解析】【分析】利用加权平均数的计算方法分别求出小华和小敏的平均数,再比较大小即可。
20.【答案】解:(Ⅰ)观察表格,可知这组样本数据的平均数是 = =15.1;
∴这组样本数据的平均数是15.1
在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为10
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5
(Ⅱ)在50名学生中,捐款多于15元的学生有15名,有300× =90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
【解析】【分析】众数是一组数据中出现次数最多的数据,是一组数据中的;中位数是指一组数据从小到大排列,位于中间的那个数;可以是一个(数据为奇数),也可以是2个的平均(数据为偶数);平均数是一组数据的和,除以这组数据的个数的值,就是平均数;计算出这50个样本数据的平均数、众数和中位数;在50名学生中,捐款多于15元的学生有15名,可以估计该校九年级300名学生在本次活动中捐款多于15元的学生人数.
21.【答案】(1)40;15
(2)解:∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
(3)解:∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为6+12+10+8+4=40,图①中m的值为100﹣30﹣25﹣20﹣10=15;
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为 =36;
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
故答案为:(1)40;15;(2)36(3)60.
【分析】(1)首先根据条形统计图求出总人数;然后由扇形统计图以及单位1,求出m的值即可;
(2)出现次数最多数据为众数,将数据按照从小到大顺序排列,中间两个数据的平均数为中位数;
(3)依据样本可知鞋号为35的学生人数比例为30%,然后依据频数=总数×百分比求解即可.
