2024年湖北省中考数学真题(无答案)
文档属性
| 名称 | 2024年湖北省中考数学真题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 600.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 09:19:28 | ||
图片预览

文档简介
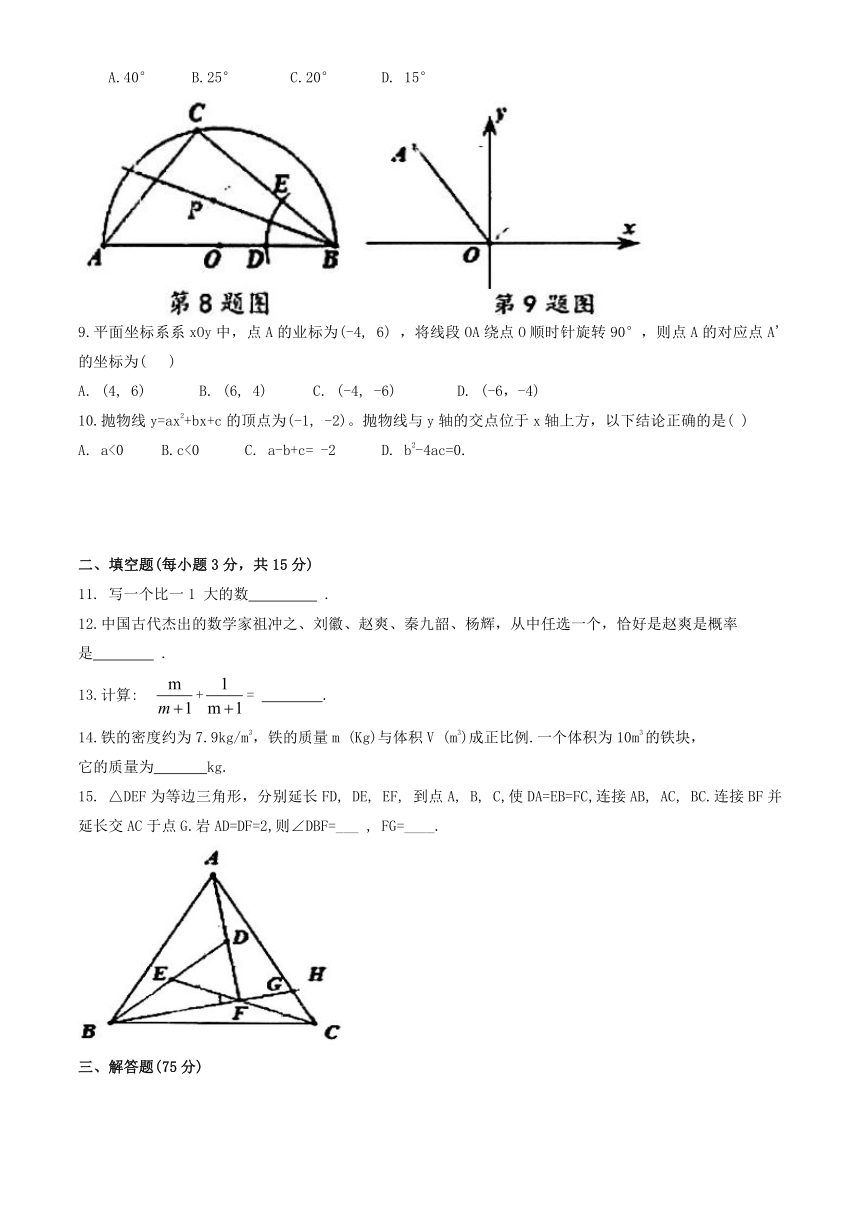
2024年湖北省中考数学试卷
一、选择题(每小题3分,共30分)
1.在生产生活中,正数和负数都有现实意义。例如收20元记作+20元,则支出10元记作( )
A. +10元 B. -10元 C. +20元 D. -20元
2.如图,是由4个相同的正方体组成的立方体图形,其主视图是( )
3.2x·3x2的值足( )
A. 5x2 B.5x3 C.6x2 D.6x3
4.如图,直线AB∥CD,已知∠1=120°. 则∠2= ( )
A.50° B.60° C.70° D.80°
5.不等式x+1≥2的解集在数轴上表示为( )
6.下列各事件是,是必然事件的是( )
A.掷一枚正方体骰子,正面朝上恰好是3 B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是红灯 D.画一个三角形,其内角和为180°
7. 《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,间牛和羊各值多少金 设每头牛值x金,每只羊值y金,可列方程为( )
8. AB为半圆0的直径,点C为半圆上一点,且∠CAB=50°.①以点B为圆心,适当长为半径作弧,交AB, BC于D,E; ②分别以DE为圆心,大于DE为半径作弧, 两弧交于点P;③作射线BP.则∠ABP= ( )
A.40° B.25° C.20° D. 15°
9.平面坐标系系xOy中,点A的业标为(-4, 6) ,将线段OA绕点O顺时针旋转90°,则点A的对应点A'的坐标为( )
A. (4, 6) B. (6, 4) C. (-4, -6) D. (-6,-4)
10.抛物线y=ax2+bx+c的顶点为(-1, -2)。抛物线与y轴的交点位于x轴上方,以下结论正确的是( )
A. a<0 B.c<0 C. a-b+c= -2 D. b2-4ac=0.
二、填空题(每小题3分,共15分)
11. 写一个比一1 大的数 .
12.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽是概率
是 .
13.计算: += .
14.铁的密度约为7.9kg/m3,铁的质量m (Kg)与体积V (m3)成正比例.一个体积为10m3的铁块,
它的质量为 kg.
15. △DEF为等边三角形,分别延长FD, DE, EF, 到点A, B, C,使DA=EB=FC,连接AB, AC, BC.连接BF并延长交AC于点G.岩AD=DF=2,则∠DBF=___ , FG=____.
三、解答题(75分)
16.计算: ( -1)×3++22 -2024°
17. ABCD中,E,F为对角线AC上两点,且AE=CF, 连接BE, DF.求证BE=DF.
18.小明为了测量树AB的高度,经过实地测量,得到两个解决方案:
方案一:如图(1),测得C地与树AB相距10米,眼睛D处观测树AB的顶端A的仰角为32°;
方案二:如图(2),测得C地与树AB相距10米,在C处放一面镜子,后退2米到达点E,眼睛D在镜子C中恰好看到树AB的项端A.
已知小明身高1.6米,试选择一个方案求出树AB的高度,(结果保留整数,tan32°≈0.64)
19.为促进学生全面发展,学校开展了丰富多彩的休育活动。为了解学生引体向上的训练成果,调查了七年级部分学生,根据成绩,分成了ABCD四组,制成了不完整的统计图。分组: 0≤A<5, 5≤B<10,10≤C<15, 15≤D<20.
(1) A组的人数为 ;
(2)七年级400人中,估计引体向上每分钟不低于10个的有多少人
(3)从众数、中位数、平均数中任选一个,说明其意义.
20.一次函数y=x+m经过点A (-3, 0) ,交反比例函数y=于点B(n, 4) .
(1)求m, n, k.
(2)点C在反比例的数y=第一象限的图像上,若S△AOC21. Rt△ABC中,∠ACB=90°, 点O在AC上,以OC为半径的圆交AB于点D,交AC于点E.
(1)求证: AB是⊙0的切线.
(2)连接OB交⊙0于点F,若AD=, AE=1,求弧CF的长.
22.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成。已知墙长42米,篱笆长80米.设垂直于墙的边AB长为x米,平行于墙的边BC为y米,围成的矩形面积为S米2.
(1)求y与x, s与x的关系式.
(2)围成的矩形花圃面积能否为750米2,若能,求出x的值.
(3)围成的矩形花圃面积是否存在最大值 若存在,求出这个最大值,并求出此时x的值.
23.如图,矩形ABCD中,E, F在AD,BC上,将四边形ABFE沿EF翻折,使E的対称点P落在CD上,B的对称点为G,PG交BC于H .
(1) 求证:△EDP∽△PCH .
(2)若P为CD中点,且AB=2,BC=3,求GH长.
(3)连接BG, 若P为DC中点,H为AB中点,探究BG与AB大小关系并説明理由.
24.如图,二次函数y=-x2+bx+3交x轴于A(-1,0)和B,交y轴于C.
(l)求b的值.
(2) M为函数图像像上一点,満足∠MAB=∠ACO,求M点的横坐标.
(3)将二次函数沿水平方向平移,新的图像记为L,L与y釉交于点N,记DC=d,记L顶点横坐标为n.
①求d与n的函数解析式.
②记L与x轴围成的图像为U,U与△ABC重合部分(不计边界)记为W,若d随n増加而増加,且W内恰有2个横坐标与纵坐标均为整数的点,宜接写出n的取值范围.
一、选择题(每小题3分,共30分)
1.在生产生活中,正数和负数都有现实意义。例如收20元记作+20元,则支出10元记作( )
A. +10元 B. -10元 C. +20元 D. -20元
2.如图,是由4个相同的正方体组成的立方体图形,其主视图是( )
3.2x·3x2的值足( )
A. 5x2 B.5x3 C.6x2 D.6x3
4.如图,直线AB∥CD,已知∠1=120°. 则∠2= ( )
A.50° B.60° C.70° D.80°
5.不等式x+1≥2的解集在数轴上表示为( )
6.下列各事件是,是必然事件的是( )
A.掷一枚正方体骰子,正面朝上恰好是3 B.某同学投篮球,一定投不中
C.经过红绿灯路口时,一定是红灯 D.画一个三角形,其内角和为180°
7. 《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,间牛和羊各值多少金 设每头牛值x金,每只羊值y金,可列方程为( )
8. AB为半圆0的直径,点C为半圆上一点,且∠CAB=50°.①以点B为圆心,适当长为半径作弧,交AB, BC于D,E; ②分别以DE为圆心,大于DE为半径作弧, 两弧交于点P;③作射线BP.则∠ABP= ( )
A.40° B.25° C.20° D. 15°
9.平面坐标系系xOy中,点A的业标为(-4, 6) ,将线段OA绕点O顺时针旋转90°,则点A的对应点A'的坐标为( )
A. (4, 6) B. (6, 4) C. (-4, -6) D. (-6,-4)
10.抛物线y=ax2+bx+c的顶点为(-1, -2)。抛物线与y轴的交点位于x轴上方,以下结论正确的是( )
A. a<0 B.c<0 C. a-b+c= -2 D. b2-4ac=0.
二、填空题(每小题3分,共15分)
11. 写一个比一1 大的数 .
12.中国古代杰出的数学家祖冲之、刘徽、赵爽、秦九韶、杨辉,从中任选一个,恰好是赵爽是概率
是 .
13.计算: += .
14.铁的密度约为7.9kg/m3,铁的质量m (Kg)与体积V (m3)成正比例.一个体积为10m3的铁块,
它的质量为 kg.
15. △DEF为等边三角形,分别延长FD, DE, EF, 到点A, B, C,使DA=EB=FC,连接AB, AC, BC.连接BF并延长交AC于点G.岩AD=DF=2,则∠DBF=___ , FG=____.
三、解答题(75分)
16.计算: ( -1)×3++22 -2024°
17. ABCD中,E,F为对角线AC上两点,且AE=CF, 连接BE, DF.求证BE=DF.
18.小明为了测量树AB的高度,经过实地测量,得到两个解决方案:
方案一:如图(1),测得C地与树AB相距10米,眼睛D处观测树AB的顶端A的仰角为32°;
方案二:如图(2),测得C地与树AB相距10米,在C处放一面镜子,后退2米到达点E,眼睛D在镜子C中恰好看到树AB的项端A.
已知小明身高1.6米,试选择一个方案求出树AB的高度,(结果保留整数,tan32°≈0.64)
19.为促进学生全面发展,学校开展了丰富多彩的休育活动。为了解学生引体向上的训练成果,调查了七年级部分学生,根据成绩,分成了ABCD四组,制成了不完整的统计图。分组: 0≤A<5, 5≤B<10,10≤C<15, 15≤D<20.
(1) A组的人数为 ;
(2)七年级400人中,估计引体向上每分钟不低于10个的有多少人
(3)从众数、中位数、平均数中任选一个,说明其意义.
20.一次函数y=x+m经过点A (-3, 0) ,交反比例函数y=于点B(n, 4) .
(1)求m, n, k.
(2)点C在反比例的数y=第一象限的图像上,若S△AOC
(1)求证: AB是⊙0的切线.
(2)连接OB交⊙0于点F,若AD=, AE=1,求弧CF的长.
22.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成。已知墙长42米,篱笆长80米.设垂直于墙的边AB长为x米,平行于墙的边BC为y米,围成的矩形面积为S米2.
(1)求y与x, s与x的关系式.
(2)围成的矩形花圃面积能否为750米2,若能,求出x的值.
(3)围成的矩形花圃面积是否存在最大值 若存在,求出这个最大值,并求出此时x的值.
23.如图,矩形ABCD中,E, F在AD,BC上,将四边形ABFE沿EF翻折,使E的対称点P落在CD上,B的对称点为G,PG交BC于H .
(1) 求证:△EDP∽△PCH .
(2)若P为CD中点,且AB=2,BC=3,求GH长.
(3)连接BG, 若P为DC中点,H为AB中点,探究BG与AB大小关系并説明理由.
24.如图,二次函数y=-x2+bx+3交x轴于A(-1,0)和B,交y轴于C.
(l)求b的值.
(2) M为函数图像像上一点,満足∠MAB=∠ACO,求M点的横坐标.
(3)将二次函数沿水平方向平移,新的图像记为L,L与y釉交于点N,记DC=d,记L顶点横坐标为n.
①求d与n的函数解析式.
②记L与x轴围成的图像为U,U与△ABC重合部分(不计边界)记为W,若d随n増加而増加,且W内恰有2个横坐标与纵坐标均为整数的点,宜接写出n的取值范围.
同课章节目录
