5.4平移 自主学习同步练习题 (含解析)人教版七年级数学下册
文档属性
| 名称 | 5.4平移 自主学习同步练习题 (含解析)人教版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 21:52:01 | ||
图片预览



文档简介
人教版七年级数学下册《5.4平移》自主学习同步练习题
一、单选题
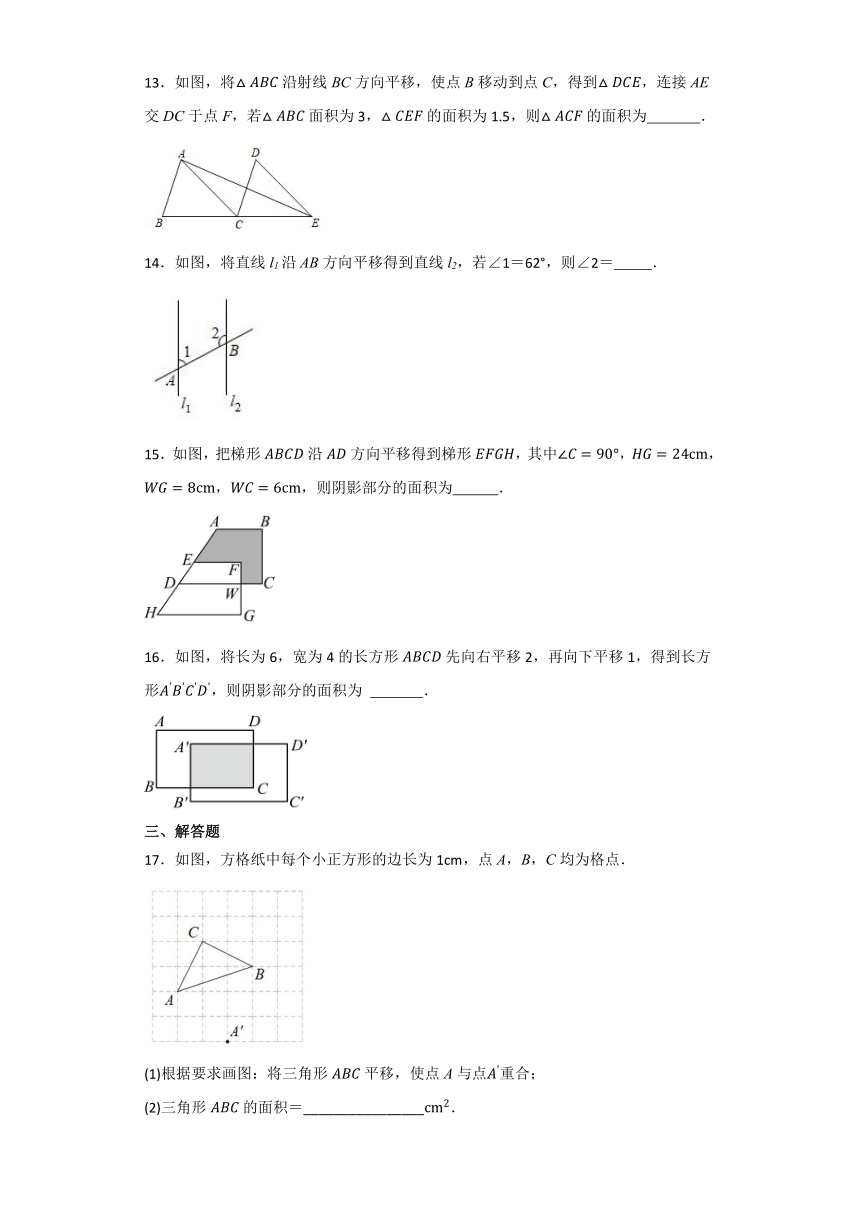
1.下列生活现象中,属于平移现象的是( )
A.急刹车时汽车在地面滑行 B.风车的转动
C.投影片的文字经投影转换到屏幕上 D.钟摆的摆动
2.下列选项中,能由原图平移得到的是( )
A. B. C. D.
3.下列车标中哪一个可以看成是由图案自身一部分经平移后得到的?( )
A. B. C. D.
4.如图,将向右平移得到,已知A,D两点的距离为1,,则的长为( )
A.5 B.4 C.3 D.2
5.如图,在一块长为11米,宽为5米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,这块草地的绿地面积是( )平方米.
A.50 B.55 C.40 D.44
6.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置,,平移距离为3,求阴影部分的面积为( )
A.10 B.12 C.15 D.18
7.如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
8.如图,是一块从一个边长为的正方形材料中剪出的垫片,经测得,则这个剪出的图形的周长是( )
A.80 B.89 C.98 D.99
二、填空题
9.将长度为5cm的线段向上平移10cm,所得线段的长度是 cm.
10.如图,在10×6的网格中,每个小方格的边长都是1个单位,写出由△DEF平移到△ABC的位置的一种方法 .
11.如图,将沿方向平移得到△,若的周长为,则四边形的周长为 .
12.如图,有一个长为20m,宽为10m的长方形草地,在草地中间有两条小路,两条小路的任何地方宽度都是1m,那么这片草地的面积是 平方米.
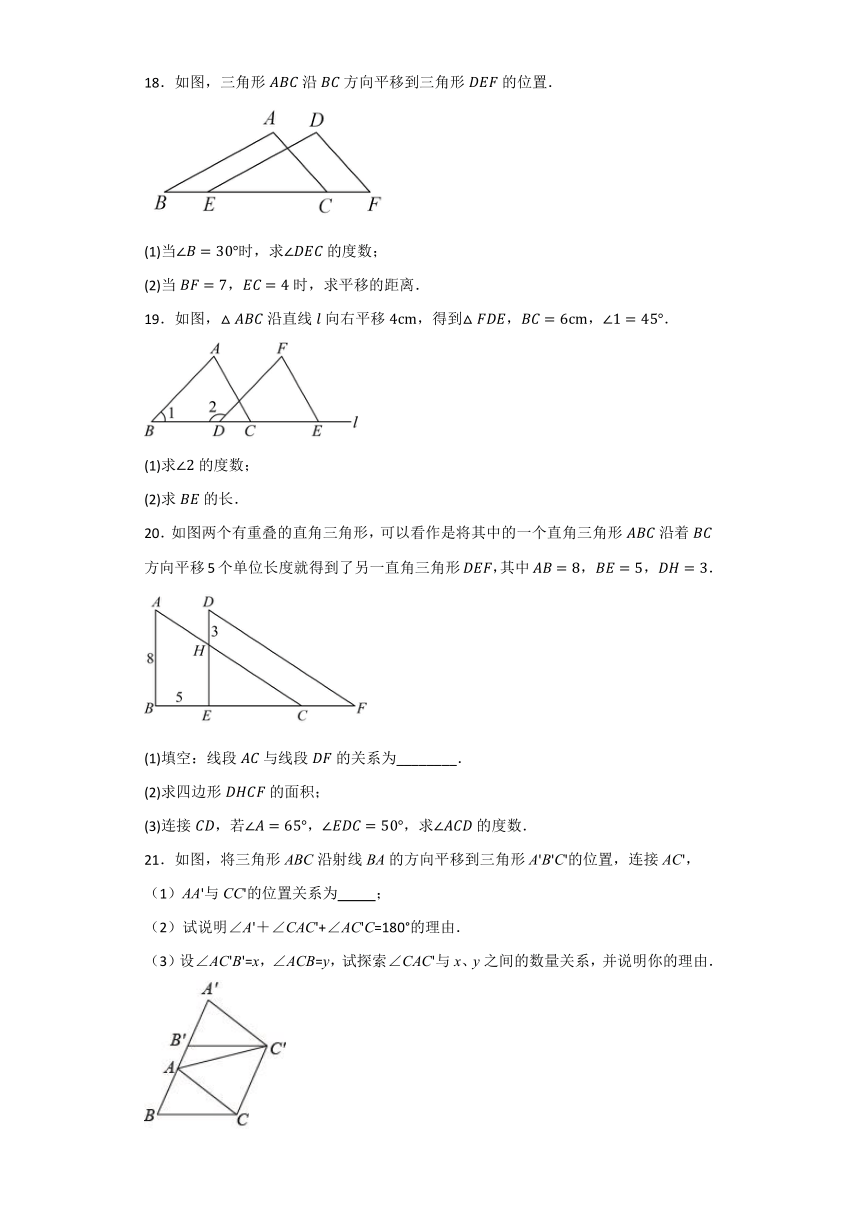
13.如图,将沿射线BC方向平移,使点B移动到点C,得到,连接AE交DC于点F,若面积为3,的面积为1.5,则的面积为 .
14.如图,将直线l1沿AB方向平移得到直线l2,若∠1=62°,则∠2= .
15.如图,把梯形沿方向平移得到梯形,其中,,,,则阴影部分的面积为 .
16.如图,将长为6,宽为4的长方形先向右平移2,再向下平移1,得到长方形,则阴影部分的面积为 .
三、解答题
17.如图,方格纸中每个小正方形的边长为1cm,点A,B,C均为格点.
(1)根据要求画图:将三角形平移,使点A与点重合;
(2)三角形的面积=________________.
18.如图,三角形沿方向平移到三角形的位置.
(1)当时,求的度数;
(2)当,时,求平移的距离.
19.如图,沿直线向右平移,得到,,.
(1)求的度数;
(2)求的长.
20.如图两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
21.如图,将三角形ABC沿射线BA的方向平移到三角形A'B'C'的位置,连接AC',
(1)AA'与CC'的位置关系为 ;
(2)试说明∠A'+∠CAC'+∠AC'C=180°的理由.
(3)设∠AC'B'=x,∠ACB=y,试探索∠CAC'与x、y之间的数量关系,并说明你的理由.
22.已知,AD//BC,∠A=∠C=120°,试回答下列问题:
(1)如图①,求证:AB//DC;
(2)如图②,若点E、F在线段AD上,且满足∠FBD=∠CBD,并且BE平分∠ABF,求∠EBD的度数;
(3)在(2)的条件下,如果平行移动DC的过程中,当∠BEA=∠BDC时,求此时∠BDC的度数.
参考答案
1.A
2.解:只有C的图形的形状和大小没有变化,符合平移的性质,属于平移得到.
故选:C.
3.解:“ ”可以看成是由图案自身一部分经平移后得到的,
故选:D.
4.解:∵将向右平移得到,
∴,
∵,
∴,
故选:B.
5.解:由题意得:
(平方米),
所以这块草地的绿地面积为50平方米,
故选A.
6.解:平移距离为3,
,
,
,
,
,
∴阴影部分的面积为.
故选:D.
7.解:(平方米),
(平方米),
∴至少要买地毯16平方米.
故选:C.
8.解:把平移到的位置,把平移到的位置,把平移到的位置,
这个垫片的周长:.
答:这个垫片的周长为.
故选:C.
9.解:将长度为5cm的线段向上平移10cm,所得线段的长度是5cm,
故答案为:5.
10.解:根据题意得,点A和点D是以对对应点,点D向右平移5个单位,再向上平移2个单位即可到达点的位置,
所以由△DEF平移到△ABC的位置的一种方法是:先把△DEF向右平移5个单位,再向上平移2个单位.
故答案为:先把△DEF向右平移5个单位,再向上平移2个单位(答案不唯一)
11.解:沿方向平移得到△,
,,
四边形的周长,
的周长,
,
四边形的周长.
故答案为:10.
12.解:小路为两个面积相等的平行四边形
小路面积为10×1×2=20m
草地面积:20×10-20=180m
故填:180
13.解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
∵面积为3,的面积为1.5,
∴△ACF的面积为1.5.
故答案为:1.5.
14.解:∵直线l1沿AB的方向平移得到直线l2
∴l1l2,
∴∠1+∠2=180°,
∴∠2=180°﹣62°=118°,
故答案为:118°
15.解:∵梯形沿方向平移得到梯形,
∴,,
∴,即,
∵,
∴,
∴,
故答案为:.
16.解:由题意可得,阴影部分是矩形,长,宽,
∴阴影部分的面积,
故答案为:.
17.(1)解:将先水平向右移动两个单位长度,再竖直向下移动两个单位长度,即可得到点A于点重合,即如图所示:
(2)解:由题意可得:,
故答案为.
18.(1)解:由平移可知,
.
(2)由平移可知,
,
,
,
平移的距离为.
19.(1)解:由平移知,,
∴.
(2)解:由平移知,.
∵,
∴.
20.(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
21.解:(1)由平移的性质可得:AA'∥CC';
故答案为:AA'∥CC';
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC'+∠AC'C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
22.解:(1)∵AD//BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB//DC.
(2)∵∠A+∠ABC=180°,∠A=120°,
∴∠ABC=60°,
∵BE平分∠ABF,
∴∠EBF=∠ABF,
∵∠FBD=∠CBD,
∴∠FBD=∠FBC,
∴∠EBF+∠FBD=(∠ABF+∠FBC)
=∠ABC=30°,
∴∠EBD=30°.
(3)∵AD//BC,
∴∠BEA=∠EBC,
∵AB∥DC,
∴∠BDC=∠ABD,
∵∠BEA=∠BDC,
∴∠EBC=∠ABD,
∴∠CBD+∠EBD=∠ABE+∠EBD,
∴∠CBD=∠ABE,
∵∠ABE=∠EBF,∠FBD=∠CBD,
∴∠ABE=∠EBF=∠FBD=∠CBD,
∵∠ABC=60°,
∴∠ABE=∠EBF=∠FBD=∠CBD=15°,
∴∠ABD=45°,
∴∠BDC=∠ABD=45°.
一、单选题
1.下列生活现象中,属于平移现象的是( )
A.急刹车时汽车在地面滑行 B.风车的转动
C.投影片的文字经投影转换到屏幕上 D.钟摆的摆动
2.下列选项中,能由原图平移得到的是( )
A. B. C. D.
3.下列车标中哪一个可以看成是由图案自身一部分经平移后得到的?( )
A. B. C. D.
4.如图,将向右平移得到,已知A,D两点的距离为1,,则的长为( )
A.5 B.4 C.3 D.2
5.如图,在一块长为11米,宽为5米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,这块草地的绿地面积是( )平方米.
A.50 B.55 C.40 D.44
6.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置,,平移距离为3,求阴影部分的面积为( )
A.10 B.12 C.15 D.18
7.如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
8.如图,是一块从一个边长为的正方形材料中剪出的垫片,经测得,则这个剪出的图形的周长是( )
A.80 B.89 C.98 D.99
二、填空题
9.将长度为5cm的线段向上平移10cm,所得线段的长度是 cm.
10.如图,在10×6的网格中,每个小方格的边长都是1个单位,写出由△DEF平移到△ABC的位置的一种方法 .
11.如图,将沿方向平移得到△,若的周长为,则四边形的周长为 .
12.如图,有一个长为20m,宽为10m的长方形草地,在草地中间有两条小路,两条小路的任何地方宽度都是1m,那么这片草地的面积是 平方米.
13.如图,将沿射线BC方向平移,使点B移动到点C,得到,连接AE交DC于点F,若面积为3,的面积为1.5,则的面积为 .
14.如图,将直线l1沿AB方向平移得到直线l2,若∠1=62°,则∠2= .
15.如图,把梯形沿方向平移得到梯形,其中,,,,则阴影部分的面积为 .
16.如图,将长为6,宽为4的长方形先向右平移2,再向下平移1,得到长方形,则阴影部分的面积为 .
三、解答题
17.如图,方格纸中每个小正方形的边长为1cm,点A,B,C均为格点.
(1)根据要求画图:将三角形平移,使点A与点重合;
(2)三角形的面积=________________.
18.如图,三角形沿方向平移到三角形的位置.
(1)当时,求的度数;
(2)当,时,求平移的距离.
19.如图,沿直线向右平移,得到,,.
(1)求的度数;
(2)求的长.
20.如图两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
21.如图,将三角形ABC沿射线BA的方向平移到三角形A'B'C'的位置,连接AC',
(1)AA'与CC'的位置关系为 ;
(2)试说明∠A'+∠CAC'+∠AC'C=180°的理由.
(3)设∠AC'B'=x,∠ACB=y,试探索∠CAC'与x、y之间的数量关系,并说明你的理由.
22.已知,AD//BC,∠A=∠C=120°,试回答下列问题:
(1)如图①,求证:AB//DC;
(2)如图②,若点E、F在线段AD上,且满足∠FBD=∠CBD,并且BE平分∠ABF,求∠EBD的度数;
(3)在(2)的条件下,如果平行移动DC的过程中,当∠BEA=∠BDC时,求此时∠BDC的度数.
参考答案
1.A
2.解:只有C的图形的形状和大小没有变化,符合平移的性质,属于平移得到.
故选:C.
3.解:“ ”可以看成是由图案自身一部分经平移后得到的,
故选:D.
4.解:∵将向右平移得到,
∴,
∵,
∴,
故选:B.
5.解:由题意得:
(平方米),
所以这块草地的绿地面积为50平方米,
故选A.
6.解:平移距离为3,
,
,
,
,
,
∴阴影部分的面积为.
故选:D.
7.解:(平方米),
(平方米),
∴至少要买地毯16平方米.
故选:C.
8.解:把平移到的位置,把平移到的位置,把平移到的位置,
这个垫片的周长:.
答:这个垫片的周长为.
故选:C.
9.解:将长度为5cm的线段向上平移10cm,所得线段的长度是5cm,
故答案为:5.
10.解:根据题意得,点A和点D是以对对应点,点D向右平移5个单位,再向上平移2个单位即可到达点的位置,
所以由△DEF平移到△ABC的位置的一种方法是:先把△DEF向右平移5个单位,再向上平移2个单位.
故答案为:先把△DEF向右平移5个单位,再向上平移2个单位(答案不唯一)
11.解:沿方向平移得到△,
,,
四边形的周长,
的周长,
,
四边形的周长.
故答案为:10.
12.解:小路为两个面积相等的平行四边形
小路面积为10×1×2=20m
草地面积:20×10-20=180m
故填:180
13.解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
∵面积为3,的面积为1.5,
∴△ACF的面积为1.5.
故答案为:1.5.
14.解:∵直线l1沿AB的方向平移得到直线l2
∴l1l2,
∴∠1+∠2=180°,
∴∠2=180°﹣62°=118°,
故答案为:118°
15.解:∵梯形沿方向平移得到梯形,
∴,,
∴,即,
∵,
∴,
∴,
故答案为:.
16.解:由题意可得,阴影部分是矩形,长,宽,
∴阴影部分的面积,
故答案为:.
17.(1)解:将先水平向右移动两个单位长度,再竖直向下移动两个单位长度,即可得到点A于点重合,即如图所示:
(2)解:由题意可得:,
故答案为.
18.(1)解:由平移可知,
.
(2)由平移可知,
,
,
,
平移的距离为.
19.(1)解:由平移知,,
∴.
(2)解:由平移知,.
∵,
∴.
20.(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
21.解:(1)由平移的性质可得:AA'∥CC';
故答案为:AA'∥CC';
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC'+∠AC'C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
22.解:(1)∵AD//BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB//DC.
(2)∵∠A+∠ABC=180°,∠A=120°,
∴∠ABC=60°,
∵BE平分∠ABF,
∴∠EBF=∠ABF,
∵∠FBD=∠CBD,
∴∠FBD=∠FBC,
∴∠EBF+∠FBD=(∠ABF+∠FBC)
=∠ABC=30°,
∴∠EBD=30°.
(3)∵AD//BC,
∴∠BEA=∠EBC,
∵AB∥DC,
∴∠BDC=∠ABD,
∵∠BEA=∠BDC,
∴∠EBC=∠ABD,
∴∠CBD+∠EBD=∠ABE+∠EBD,
∴∠CBD=∠ABE,
∵∠ABE=∠EBF,∠FBD=∠CBD,
∴∠ABE=∠EBF=∠FBD=∠CBD,
∵∠ABC=60°,
∴∠ABE=∠EBF=∠FBD=∠CBD=15°,
∴∠ABD=45°,
∴∠BDC=∠ABD=45°.
