2024年四川省乐山市中考数学真题试题(含答案)
文档属性
| 名称 | 2024年四川省乐山市中考数学真题试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 834.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 09:22:36 | ||
图片预览




文档简介
乐山市2024年初中学业水平考试
数学
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共8页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.考生作答时,不能使用任何型号的计算器.
第Ⅰ卷(选择题共30分)
注意事项:
1.选择题必须使用2B铅笔将答案标号填涂在答题卡对应题目标号的位置上.
2.在每小题给出的四个选项中,只有一个选项符合题目要求.
一、选择题:本大题共10个小题,每小题3分,共30分.
1.不等式的解集是( )
A. B. C. D.
2.下列文物中,俯视图是四边形的是( )
A.带盖玉柱形器 B.白衣彩陶钵
C.镂空人面覆盆陶器 D.青铜大方鼎
3.2023年,乐山市在餐饮、文旅、体育等服务消费表现亮眼,网络零售额突破400亿元,居全省地级市第一.将40000000000用科学记数法表示为( )
A. B. C. D.
4.下列多边形中,内角和最小的是( )
A. B. C. D.
5.为了解学生上学的交通方式,刘老师在九年级800名学生中随机抽取了60名进行问卷调查,并将调查结果制作成如下统计表,估计该年级学生乘坐公交车上学的人数为( )
交通方式 公交车 自行车 步行 私家车 其它
人数(人) 30 5 15 8 2
A.100 B.200 C.300 D.400
6.如图1,下列条件中不能判定四边形ABCD为平行四边形的是( )
图1
A., B.,
C., D.,
7.已知,化简的结果为( )
A. B.1 C. D.
8.若关于x的一元二次方程两根为、,且,则p的值为( )
A. B. C. D.6
9.已知二次函数,当时,函数取得最大值;当时,函数取得最小值,则t的取值范围是( )
A. B. C. D.
10.如图2,在菱形ABCD中,,,点P是BC边上一个动点,在BC延长线上找一点Q,使得点P和点Q关于点C对称,连结DP、AQ交于点M.当点P从B点运动到C点时,点M的运动路径长为( )
A. B. C. D.
第Ⅱ卷(非选择题共120分)
注意事项:
1.考生使用0.5mm黑色墨汁签字笔在答题卡上题目所指示的答题区域内作答,答在试题卷上无效.
2.作图时,可先用铅笔画线,确认后再用0.5mm黑色墨汁签字笔描清楚.
3.解答题应写出文字说明、证明过程或推演步骤.
4.本部分共16个小题,共120分.
二、填空题:本大题共6个小题,每小题3分,共18分.
11.计算:______.
12.一名交警在路口随机监测了5辆过往车辆的速度,分别是:66,57,71,69,58(单位:千米/时).那么这5辆车的速度的中位数是______.
13.如图3,两条平行线a、b被第三条直线c所截.若,那么______.
图3
14.已知,,则______.
15.如图4,在梯形ABCD中,,对角线AC和BD交于点O,若,则______.
图4
16.定义:函数图象上到两坐标轴的距离都小于或等于1的点叫做这个函数图象的“近轴点”.
例如,点是函数图象的“近轴点”.
(1)下列三个函数的图象上存在“近轴点”的是______(填序号);
①;②;③.
(2)若一次函数图象上存在“近轴点”,则m的取值范围为______.
三、解答题:本大题共10个小题,共102分.解答应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分9分)
计算:.
18.(本小题满分9分)
解方程组:
19.(本小题满分9分)
如图5,AB是的平分线,,求证:.
图5
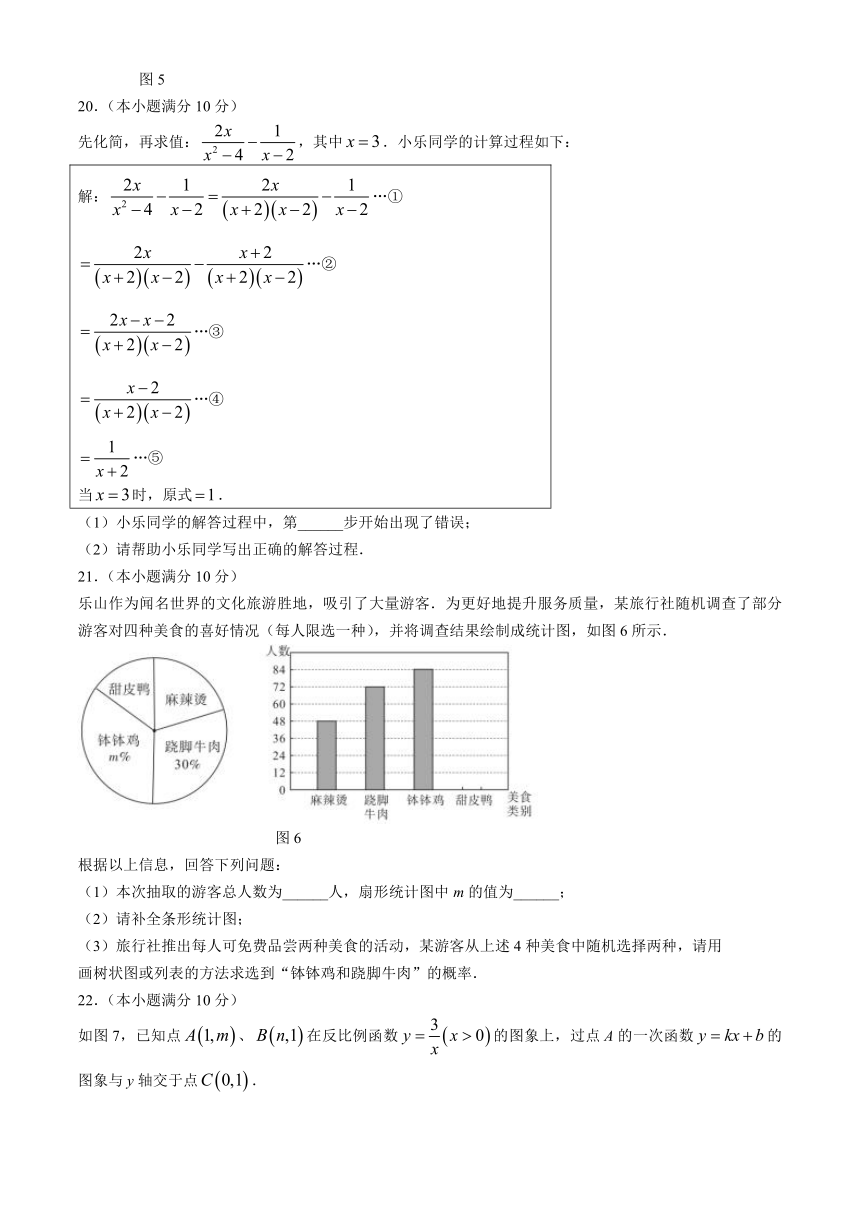
20.(本小题满分10分)
先化简,再求值:,其中.小乐同学的计算过程如下:
解:…① …② …③ …④ …⑤ 当时,原式.
(1)小乐同学的解答过程中,第______步开始出现了错误;
(2)请帮助小乐同学写出正确的解答过程.
21.(本小题满分10分)
乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图6所示.
图6
根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为______人,扇形统计图中m的值为______;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用
画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
22.(本小题满分10分)
如图7,已知点、在反比例函数的图象上,过点A的一次函数的图象与y轴交于点.
图7
(1)求m、n的值和一次函数的表达式;
(2)连结AB,求点C到线段AB的距离.
23.(本小题满分10分)
我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图8.1,请你根据词意计算秋千绳索OA的长度;
(2)如图8.2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索OA的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
图8.1 图8.2
24.(本小题满分10分)
如图9,是的外接圆,AB为直径,过点C作的切线CD交BA延长线于点D,点E为上一点,且.
图9
(1)求证:;
(2)若EF垂直平分OB,,求阴影部分的面积.
25.(本小题满分12分)
在平面直角坐标系xOy中,我们称横坐标、纵坐标都为整数的点为“完美点”.抛物线(a为常数且)与y轴交于点A.
(1)若,求抛物线的顶点坐标;
(2)若线段OA(含端点)上的“完美点”个数大于3个且小于6个,求a的取值范围;
(3)若抛物线与直线交于M、N两点,线段MN与抛物线围成的区域(含边界)内恰有4个“完美点”,求a的取值范围.
备用图1 备用图2
26.(本小题满分13分)
在一堂平面几何专题复习课上,刘老师先引导学生解决了以下问题:
【问题情境】
如图10.1,在中,,,点D、E在边BC上,且,,,求DE的长.
解:如图10.2,将绕点A逆时针旋转90°得到,连结.
图10.1
由旋转的特征得,,,.
∵,,∴.
∵,∴,即.∴.
在和中,,,,
∴___①___.
∴.
又∵,
∴在中,___②___.
∵,,
图10.2
∴___③___.
【问题解决】
上述问题情境中,“①”处应填:______;“②”处应填:______;“③”处应填:______.
刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】
如图10.3,在正方形ABCD中,点E、F分别在边BC、CD上,满足的周长等于正方形ABCD的周长的一半,连结AE、AF,分别与对角线BD交于M、N两点.探究BM、MN、DN的数量关系并证明.
图10.3
【拓展应用】
如图10.4,在矩形ABCD中,点E、F分别在边BC、CD上,且.探究BE、EF、DF的数量关系:______(直接写出结论,不必证明).
图10.4
【问题再探】
如图10.5,在中,,,,点D、E在边AC上,且.设,,求y与x的函数关系式.
图10.5
乐山市2024年初中学业水平考试
数学参考答案及评分标准
第Ⅰ卷(选择题共30分)
一、选择题:本大题共10小题,每小题3分,共30分.
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C A D D B A C B
第Ⅱ卷(非选择题共120分)
二、填空题:本大题共6小题,每小题3分,共18分.
11.3a;12.66;13.120°;14.29;15.,16.(1)③;(2)或.
注:16题第(1)空1分,第(2)空2分.
三、解答题:本大题共10个小题,共102分.解答应写出必要的文字说明,证明过程或演算步骤.
17.解:原式…6分
.…9分
注:第一步含有三个式子的计算,答对一个得2分.
18.解:
解法一:①+②,得,解得.…3分
将代入①,得.…6分
∴.…9分
解法二:由①,得③.
将③代入②,得,解得.…3分
将代入③,得.…6分
∴…9分
19.证明:∵AB是的平分线,∴.…3分
∴在和中,,,,
∴(SAS)…7分
∴…9分
20.解:(1)第③步开始出现了错误.…3分
(2)…4分
…5分
…6分
…7分
.…8分
当时,原式.…10分
21.解:(1)总人数为240人,m的值为35.……2分
(2)如下图所示.
(3)记A:麻辣烫,B:跷脚牛肉,C:钵钵鸡,D:甜皮鸭.
解法一:由题可得树状图:
P(选到“钵钵鸡和跷脚牛肉”).…10分
解法二:由题可列表:
第一次 第二次 A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
…8分
P(选到“钵钵鸡和跷脚牛肉”)=.…10分
22.解:(1)∵点、在反比例函数图象上,
∴,.…2分
又∵一次函数过点,,
∴解得…4分
∴一次函数表达式为.……5分
(2)如图,连结BC.
过点A作,垂足为点D,过点C作,垂足为点E.
∵,,∴轴,.…6分
∵点,,,
∴点,,.
在中,.7分
又∵,8分
即,
∴,即点C到线段AB的距离为.…10分
23.解:(1)如图,过点作,垂足为点B.
设秋千绳索的长度为x尺.
由题可知,,,,∴.
在中,由勾股定理得:
∴.…3分
解得.
答:秋千绳索的长度为14.5尺…5分
(2)能.…6分
由题可知,,.
在中,…7分
同理,.…8分
∵,∴.…9分
∴.…10分
24.证明:(1)如图,连结OC.
∵CD为的切线,点C在上,
∴,即.…1分
又∵AB为直径,∴,即.
∴.…2分
∵,∴.…3分
∵,∴.…4分
∴.∴.…5分
(2)连结OE、BE.
∵EF垂直平分OB,∴.
又∵,∴为等边三角形.
∴,.…6分
∵,∴.
∵,∴.
又∵,∴.
∵,∴为等边三角形.
∴,.∴.
∴.∴.…8分
∴.∴.
又∵,…10分
∴.
25.解:(1)当时,抛物线.…2分
∴顶点坐标.…3分
(2)由题可知.
∵线段OA上的“完美点”的个数大于3个且小于6个,
∴“完美点”的个数为4个或5个.…4分
∴当“完美点”个数为4个时,分别为,,,;
当“完美点”个数为5个时,分别为,,,,.
∴.…6分
∴a的取值范围是.…7分
(3)易知抛物线的顶点坐标为,过点,,.
显然,“完美点”,,符合题意.
下面讨论抛物线经过,的两种情况:
①当抛物线经过时,解得此时,,,.
如图所示,满足题意的“完美点”有,,,,共4个.…9分
②当抛物线经过时,解得此时,,,.
如图所示,满足题意的“完美点”有,,,,,,共6个.…11分
∴a的取值范围是.……12分
26.解:(1)①;②;③5.…3分
(2).…4分
证明:如图,将绕点A逆时针旋转90°,得到.
过点D作交边于点H,连结NH.
由旋转的特征得,,.
由题意得,
∴.
在和中,,,,
∴(SSS).…5分
∴.
又∵BD为正方形ABCD的对角线,
∴.
∵,
∴.
在和中,,,,
∴(ASA).…6分
∴,.
在和中,,,,
∴(SAS).…7分
∴.
在中,,∴.……8分
(3).…10分
(4)如图,将绕点B逆时针旋转90°,得到,连结.
过点E作,垂足为点G,过点作,垂足为.
过点作,过点D作交AB于点H,、DF交于点F.
由旋转的特征得,,,.
∵,,∴.
∴,,即.
在和中,,,,
∴(SAS).
∵,,,∴.
又∵,,∴.
∵,∴,.
∴.
∴,即,.
∴.
同理可得,.
∴,.
∵,,∴.
又∵,,
∴四边形为矩形.
∴,,,
.
在中,.
∴.
解得.……13分
数学
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共8页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.考生作答时,不能使用任何型号的计算器.
第Ⅰ卷(选择题共30分)
注意事项:
1.选择题必须使用2B铅笔将答案标号填涂在答题卡对应题目标号的位置上.
2.在每小题给出的四个选项中,只有一个选项符合题目要求.
一、选择题:本大题共10个小题,每小题3分,共30分.
1.不等式的解集是( )
A. B. C. D.
2.下列文物中,俯视图是四边形的是( )
A.带盖玉柱形器 B.白衣彩陶钵
C.镂空人面覆盆陶器 D.青铜大方鼎
3.2023年,乐山市在餐饮、文旅、体育等服务消费表现亮眼,网络零售额突破400亿元,居全省地级市第一.将40000000000用科学记数法表示为( )
A. B. C. D.
4.下列多边形中,内角和最小的是( )
A. B. C. D.
5.为了解学生上学的交通方式,刘老师在九年级800名学生中随机抽取了60名进行问卷调查,并将调查结果制作成如下统计表,估计该年级学生乘坐公交车上学的人数为( )
交通方式 公交车 自行车 步行 私家车 其它
人数(人) 30 5 15 8 2
A.100 B.200 C.300 D.400
6.如图1,下列条件中不能判定四边形ABCD为平行四边形的是( )
图1
A., B.,
C., D.,
7.已知,化简的结果为( )
A. B.1 C. D.
8.若关于x的一元二次方程两根为、,且,则p的值为( )
A. B. C. D.6
9.已知二次函数,当时,函数取得最大值;当时,函数取得最小值,则t的取值范围是( )
A. B. C. D.
10.如图2,在菱形ABCD中,,,点P是BC边上一个动点,在BC延长线上找一点Q,使得点P和点Q关于点C对称,连结DP、AQ交于点M.当点P从B点运动到C点时,点M的运动路径长为( )
A. B. C. D.
第Ⅱ卷(非选择题共120分)
注意事项:
1.考生使用0.5mm黑色墨汁签字笔在答题卡上题目所指示的答题区域内作答,答在试题卷上无效.
2.作图时,可先用铅笔画线,确认后再用0.5mm黑色墨汁签字笔描清楚.
3.解答题应写出文字说明、证明过程或推演步骤.
4.本部分共16个小题,共120分.
二、填空题:本大题共6个小题,每小题3分,共18分.
11.计算:______.
12.一名交警在路口随机监测了5辆过往车辆的速度,分别是:66,57,71,69,58(单位:千米/时).那么这5辆车的速度的中位数是______.
13.如图3,两条平行线a、b被第三条直线c所截.若,那么______.
图3
14.已知,,则______.
15.如图4,在梯形ABCD中,,对角线AC和BD交于点O,若,则______.
图4
16.定义:函数图象上到两坐标轴的距离都小于或等于1的点叫做这个函数图象的“近轴点”.
例如,点是函数图象的“近轴点”.
(1)下列三个函数的图象上存在“近轴点”的是______(填序号);
①;②;③.
(2)若一次函数图象上存在“近轴点”,则m的取值范围为______.
三、解答题:本大题共10个小题,共102分.解答应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分9分)
计算:.
18.(本小题满分9分)
解方程组:
19.(本小题满分9分)
如图5,AB是的平分线,,求证:.
图5
20.(本小题满分10分)
先化简,再求值:,其中.小乐同学的计算过程如下:
解:…① …② …③ …④ …⑤ 当时,原式.
(1)小乐同学的解答过程中,第______步开始出现了错误;
(2)请帮助小乐同学写出正确的解答过程.
21.(本小题满分10分)
乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图6所示.
图6
根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为______人,扇形统计图中m的值为______;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用
画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
22.(本小题满分10分)
如图7,已知点、在反比例函数的图象上,过点A的一次函数的图象与y轴交于点.
图7
(1)求m、n的值和一次函数的表达式;
(2)连结AB,求点C到线段AB的距离.
23.(本小题满分10分)
我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图8.1,请你根据词意计算秋千绳索OA的长度;
(2)如图8.2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索OA的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
图8.1 图8.2
24.(本小题满分10分)
如图9,是的外接圆,AB为直径,过点C作的切线CD交BA延长线于点D,点E为上一点,且.
图9
(1)求证:;
(2)若EF垂直平分OB,,求阴影部分的面积.
25.(本小题满分12分)
在平面直角坐标系xOy中,我们称横坐标、纵坐标都为整数的点为“完美点”.抛物线(a为常数且)与y轴交于点A.
(1)若,求抛物线的顶点坐标;
(2)若线段OA(含端点)上的“完美点”个数大于3个且小于6个,求a的取值范围;
(3)若抛物线与直线交于M、N两点,线段MN与抛物线围成的区域(含边界)内恰有4个“完美点”,求a的取值范围.
备用图1 备用图2
26.(本小题满分13分)
在一堂平面几何专题复习课上,刘老师先引导学生解决了以下问题:
【问题情境】
如图10.1,在中,,,点D、E在边BC上,且,,,求DE的长.
解:如图10.2,将绕点A逆时针旋转90°得到,连结.
图10.1
由旋转的特征得,,,.
∵,,∴.
∵,∴,即.∴.
在和中,,,,
∴___①___.
∴.
又∵,
∴在中,___②___.
∵,,
图10.2
∴___③___.
【问题解决】
上述问题情境中,“①”处应填:______;“②”处应填:______;“③”处应填:______.
刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】
如图10.3,在正方形ABCD中,点E、F分别在边BC、CD上,满足的周长等于正方形ABCD的周长的一半,连结AE、AF,分别与对角线BD交于M、N两点.探究BM、MN、DN的数量关系并证明.
图10.3
【拓展应用】
如图10.4,在矩形ABCD中,点E、F分别在边BC、CD上,且.探究BE、EF、DF的数量关系:______(直接写出结论,不必证明).
图10.4
【问题再探】
如图10.5,在中,,,,点D、E在边AC上,且.设,,求y与x的函数关系式.
图10.5
乐山市2024年初中学业水平考试
数学参考答案及评分标准
第Ⅰ卷(选择题共30分)
一、选择题:本大题共10小题,每小题3分,共30分.
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C A D D B A C B
第Ⅱ卷(非选择题共120分)
二、填空题:本大题共6小题,每小题3分,共18分.
11.3a;12.66;13.120°;14.29;15.,16.(1)③;(2)或.
注:16题第(1)空1分,第(2)空2分.
三、解答题:本大题共10个小题,共102分.解答应写出必要的文字说明,证明过程或演算步骤.
17.解:原式…6分
.…9分
注:第一步含有三个式子的计算,答对一个得2分.
18.解:
解法一:①+②,得,解得.…3分
将代入①,得.…6分
∴.…9分
解法二:由①,得③.
将③代入②,得,解得.…3分
将代入③,得.…6分
∴…9分
19.证明:∵AB是的平分线,∴.…3分
∴在和中,,,,
∴(SAS)…7分
∴…9分
20.解:(1)第③步开始出现了错误.…3分
(2)…4分
…5分
…6分
…7分
.…8分
当时,原式.…10分
21.解:(1)总人数为240人,m的值为35.……2分
(2)如下图所示.
(3)记A:麻辣烫,B:跷脚牛肉,C:钵钵鸡,D:甜皮鸭.
解法一:由题可得树状图:
P(选到“钵钵鸡和跷脚牛肉”).…10分
解法二:由题可列表:
第一次 第二次 A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
…8分
P(选到“钵钵鸡和跷脚牛肉”)=.…10分
22.解:(1)∵点、在反比例函数图象上,
∴,.…2分
又∵一次函数过点,,
∴解得…4分
∴一次函数表达式为.……5分
(2)如图,连结BC.
过点A作,垂足为点D,过点C作,垂足为点E.
∵,,∴轴,.…6分
∵点,,,
∴点,,.
在中,.7分
又∵,8分
即,
∴,即点C到线段AB的距离为.…10分
23.解:(1)如图,过点作,垂足为点B.
设秋千绳索的长度为x尺.
由题可知,,,,∴.
在中,由勾股定理得:
∴.…3分
解得.
答:秋千绳索的长度为14.5尺…5分
(2)能.…6分
由题可知,,.
在中,…7分
同理,.…8分
∵,∴.…9分
∴.…10分
24.证明:(1)如图,连结OC.
∵CD为的切线,点C在上,
∴,即.…1分
又∵AB为直径,∴,即.
∴.…2分
∵,∴.…3分
∵,∴.…4分
∴.∴.…5分
(2)连结OE、BE.
∵EF垂直平分OB,∴.
又∵,∴为等边三角形.
∴,.…6分
∵,∴.
∵,∴.
又∵,∴.
∵,∴为等边三角形.
∴,.∴.
∴.∴.…8分
∴.∴.
又∵,…10分
∴.
25.解:(1)当时,抛物线.…2分
∴顶点坐标.…3分
(2)由题可知.
∵线段OA上的“完美点”的个数大于3个且小于6个,
∴“完美点”的个数为4个或5个.…4分
∴当“完美点”个数为4个时,分别为,,,;
当“完美点”个数为5个时,分别为,,,,.
∴.…6分
∴a的取值范围是.…7分
(3)易知抛物线的顶点坐标为,过点,,.
显然,“完美点”,,符合题意.
下面讨论抛物线经过,的两种情况:
①当抛物线经过时,解得此时,,,.
如图所示,满足题意的“完美点”有,,,,共4个.…9分
②当抛物线经过时,解得此时,,,.
如图所示,满足题意的“完美点”有,,,,,,共6个.…11分
∴a的取值范围是.……12分
26.解:(1)①;②;③5.…3分
(2).…4分
证明:如图,将绕点A逆时针旋转90°,得到.
过点D作交边于点H,连结NH.
由旋转的特征得,,.
由题意得,
∴.
在和中,,,,
∴(SSS).…5分
∴.
又∵BD为正方形ABCD的对角线,
∴.
∵,
∴.
在和中,,,,
∴(ASA).…6分
∴,.
在和中,,,,
∴(SAS).…7分
∴.
在中,,∴.……8分
(3).…10分
(4)如图,将绕点B逆时针旋转90°,得到,连结.
过点E作,垂足为点G,过点作,垂足为.
过点作,过点D作交AB于点H,、DF交于点F.
由旋转的特征得,,,.
∵,,∴.
∴,,即.
在和中,,,,
∴(SAS).
∵,,,∴.
又∵,,∴.
∵,∴,.
∴.
∴,即,.
∴.
同理可得,.
∴,.
∵,,∴.
又∵,,
∴四边形为矩形.
∴,,,
.
在中,.
∴.
解得.……13分
同课章节目录
