期末高频考点检测卷(含答案)2023-2024学年数学四年级下册青岛版
文档属性
| 名称 | 期末高频考点检测卷(含答案)2023-2024学年数学四年级下册青岛版 |

|
|
| 格式 | docx | ||
| 文件大小 | 407.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末高频考点检测卷(试题)2023-2024学年数学四年级下册青岛版
一、选择题
1.如图,幸福小区有一个花园,由3个大小不同的等边三角形组成。从甲地到乙地,下列说法错误的是( )。
A.①号路长60米 B.①号路和③号路一样长 C.②号路最短
2.已知△×○=16,下面选项正确的( )。
A.16÷○=△ B.△×16=○ C.○×16=△
3.李师傅每天做m个零件比刘师傅每天少做n个,刘师傅每天做( )个零件。
A.m+n B.m-n C.m-n+m
4.下面可以用式子5x+10表示的是( )。
A.一辆汽车每小时行驶x千米,这辆汽车5小时行驶的路程。
B.一个西瓜10元,一箱苹果x元,买5箱苹果和一个西瓜一共需要的钱数。
C.幼儿园有x个小朋友,每人分了5个面包,还剩下10个面包,一共分的面包数。
5.在一次百米赛跑中,前三名分别是甲(12.61秒)、乙(13.08秒)、丙(12.58秒),第一名是( )。
A.丙 B.乙 C.甲
6.在一组数据中,最大的一个数是67,最小的一个数是52,这组数据的平均数可能是( )。
A.68 B.59 C.52
7.下列选项中的三条线段能围成等腰三角形的是( )。
A.3cm、3cm、7cm B.2cm、3cm、4cm C.4cm、4cm、7cm
8.下面等式中只运用了乘法结合律的是( )。
A.5×6×4=3×4×10
B.(3×4)×8×5=3×(4×5)×8
C.4×(25×3)=(4×25)×3
二、填空题
9.丁丁今年a岁,妈妈今年b岁,那么15年以后妈妈比丁丁大( )岁。
10.一个正方形的边长是a米,它的周长是( )米,面积是( )平方米;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,正方形的面积是( )平方米。
11.已知∠1和∠2是直角三角形中的两个锐角。∠1=35°,∠2=( )°。
12.一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是( )厘米。
13.下面的竖式在计算过程中运用了乘法分配律,列出相应的算式:( )。
14.不计算,在括号里填上“>”“<”或“=”。
720-35÷5( )720÷(3×5)
76×12×5( )76×(12×5)
75×(8+3)( )75×8+3
960-(326-128)( )960-326-128
15.找规律,填一填。
12×101=1212
24×101=2424
36×101=3636
48×101=( )
( )×101=9696
16.光明小学三年级1班的学生组织聚餐,某餐馆有一种长方形桌子,每张桌子周围放4把椅子。如果客人多,就按照如图所示的方式拼桌。
三年级1班一共有44名同学,一共需要拼( )张桌子。
三、计算题
17.直接写得数。
①25×4= ②5×m×n= ③a×6×5= ④102=
⑤82= ⑥99+68= ⑦125×9×8= ⑧36+64-36+64=
18.用竖式计算。(带“※”的要验算)
15.38+4.96= 21.28-3.49= ※40.02-21.38=
19.用你喜欢的方法计算,能简算的一定要简算。
(1)580÷5÷2 (2)32×25×3
(3)34×75+67×75-75 (4)65×101
四、解答题
20.一个等腰三角形,它的顶角度数是58度。它的一个底角的度数是多少?
21.仓库里有货物96吨,运走了12车,每车运b吨。
(1)用式子表示仓库里剩下的吨数。
(2)利用这个式子,求当b=5时,仓库里剩下的货物有多少吨?
22.下面是青青在超市的购物情况
商品 数量(千克) 单价(元)
樱桃 m 12
草莓 n 8
(1)用含有字母的式子表示青青一共花的钱数。
(2)当m=5,n=3时,如果付给售货员100元,那么应找回多少元?
23.我国的“五岳”中,泰山海拔高度为1.545千米,衡山海拔高度为1.29千米,恒山的海拔高度比泰山和衡山海拔高度的和少0.818千米,恒山的海拔高度是多少千米?
24.看下表回答问题。
文具 单价(元)
钢笔 8.80
三角尺 1.60
橡皮 0.50
(1)一支钢笔比三角尺和橡皮多多少元?
(2)你还能提出什么问题?(解答)
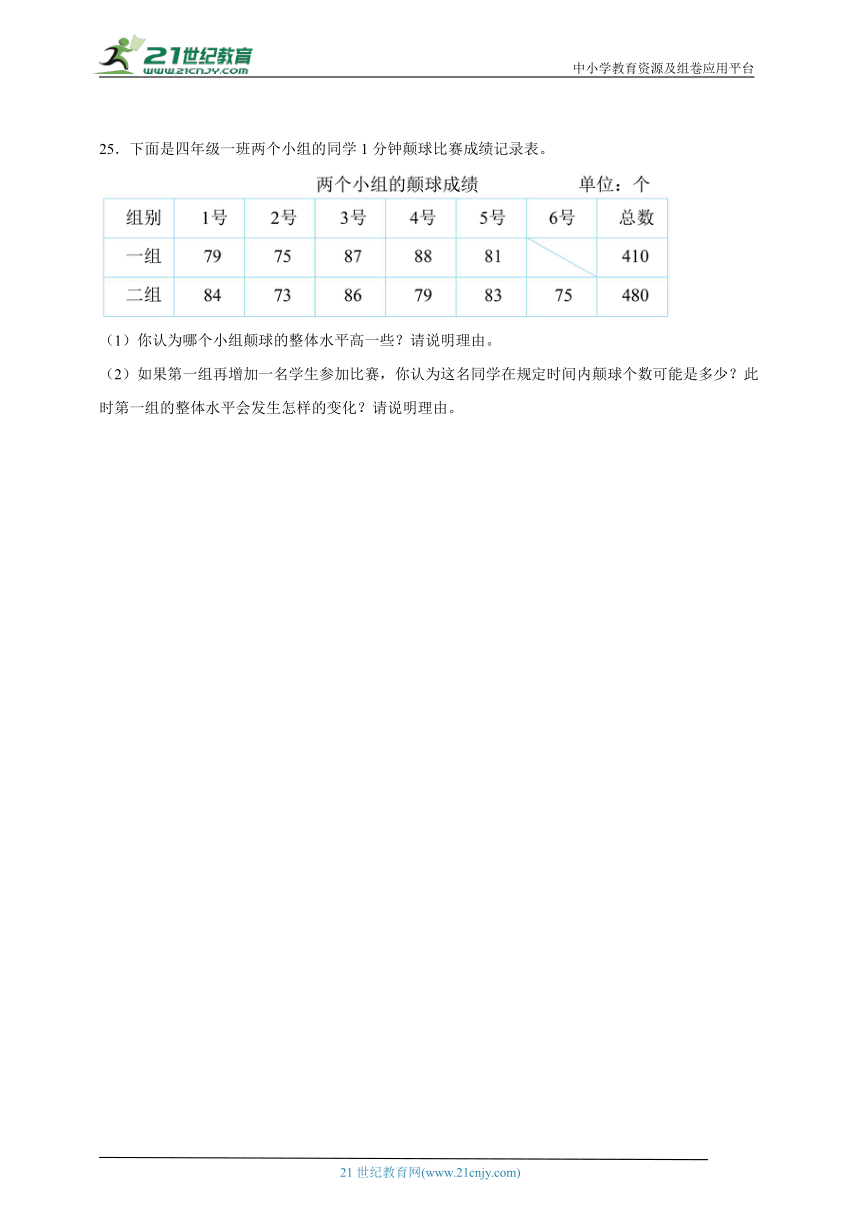
25.下面是四年级一班两个小组的同学1分钟颠球比赛成绩记录表。
(1)你认为哪个小组颠球的整体水平高一些?请说明理由。
(2)如果第一组再增加一名学生参加比赛,你认为这名同学在规定时间内颠球个数可能是多少?此时第一组的整体水平会发生怎样的变化?请说明理由。
参考答案:
1.A
【分析】观察图形可知,①号路长(20+40+20+40)米;③号路长(2×40+2×20)米,从而对A和B作出判断;再求出②号路长(20+40)米,然后与①、②号路的长度进行比较,对C作出判断即可。
【详解】A.20+40+20+40
=60+20+40
=80+40
=120(米)
符合题意;
B.①号路长:
20+40+20+40
=60+60
=120(米)
③号路长:
2×40+2×20
=80+40
=120(米)
①号路和③号路一样长,不符合题意;
C.20+40=60(米)
60<120,所以②号路最短,不符合题意。
幸福小区有一个花园,由3个大小不同的等边三角形组成。从甲地到乙地,下列说法错误的是①号路长60米。
故答案为:A
2.A
【分析】乘数×乘数=积,积÷乘数=乘数。根据△×○=16,有○×△=16,16÷△=○,16÷○=△。
【详解】已知△×○=16,选项正确的是16÷○=△。
故答案为:A
3.A
【分析】根据题意刘师傅做的零件个数=李师傅做的零件个数+李师傅每天做零件比刘师傅每天少做n个,根据等量关系式代入法即可解答。
【详解】刘师傅每天做(m+n)个。
故答案为:A
4.B
【分析】根据路程=时间×速度,总价=单价×数量,分析每个选项,列式选出符合题意的即可。
【详解】A.一辆汽车每小时行驶x千米,这辆汽车5小时行驶的路程为5x千米,不符合题意;
B.买5箱苹果需要5x元,买5箱苹果和一个西瓜一共需要(5x+10)元,符合题意;
C.一共分了5x个面包,不符合题意。
可以用式子5x+10表示的是一个西瓜10元,一箱苹果x元,买5箱苹果和一个西瓜一共需要的钱数。
故答案为:B
5.A
【分析】小数大小的比较方法,先看小数的整数部分,整数部分大的这个数就大,整数部分相同的就看十分位,十分位大的这个数就大,十分位相同的就看百分位,百分位大的这个数就大……,据此判断出前三名同学用的时间的长短,然后根据路程一定时,谁用的时间越短,则谁的速度越快,据此解答即可。
【详解】12.58<12.61<13.08
根据分析得,这次百米赛跑前三名分别是丙(12.58秒)、甲(12.61秒)、乙(13.08秒),第一名是丙。
故答案为:A
6.B
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;其特点是比最大数小,比最小数大;依此选择。
【详解】A.68>67,因此这组数据的平均数不可能是68。
B.52<59<67,因此这组数据的平均数可能是59。
C.52=52,因此这组数据的平均数不可能是52。
这组数据的平均数可能是59。
故答案为:B
7.C
【分析】根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边才能构成三角形;等腰三角形有两条边相等。据此分析并选择即可。
【详解】A.3+3=6,6<7,这三条线段不能围成三角形;
B.2+3=5,5>4;这三条线段能围成三角形,但没有相等的边,不能围成等腰三角形;
C.4+4=8,8>7;这三条线段能围成三角形,并且有两条相等的边,能围成等腰三角形;
则三条线段能围成等腰三角形的是4cm、4cm、7cm。
故答案为:C
8.C
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。乘法交换律是指两个数相乘,交换乘数的位置,它们的积不变。据此逐项分析解答。
【详解】A.将6看成2×3,根据乘法交换律和乘法结合律可知:5×6×4=5×(2×3)×4=(5×2)×3×4=10×3×4=3×4×10,
B.(3×4)×8×5=3×(4×5)×8,先根据乘法交换律交换8和5的位置,再根据乘法结合律,先计算4×5。
C.4×(25×3)=(4×25)×3,根据乘法结合律,先计算4×25。乘数位置不变,没有运用乘法交换律。
只运用了乘法结合律的是4×(25×3)=(4×25)×3。
故答案为:C
9.b-a
【分析】两个人的年龄差是一个定数,不随时间的变化而变化,要求15年后妈妈比丁丁大多少岁,用妈妈今年的岁数减去丁丁今年的岁数,求出今年妈妈比丁丁大多少岁,也就是15年以后妈妈比丁丁大的岁数。
【详解】b-a
丁丁今年a岁,妈妈今年b岁,那么15年以后妈妈比丁丁大(b-a)岁。
10. 4a/4 a/4×a a2/a a c2/c c
【分析】正方形的周长=边长×4,正方形的面积=边长×边长。直接代入公式即可;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,那么这个正方形的边长是c米。再根据正方形的面积=边长×边长求解即可。
【详解】a×4=4a,a×a= a2,c×c= c2
一个正方形的边长是a米,它的周长是4a米,面积是a2平方米;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,正方形的面积是c2平方米。
11.55
【分析】直角三角形中有一个直角,根据三角形的内角和为180°可知,∠2=180°-90°-∠1。
【详解】∠2=180°-90°-∠1=180°-90°-35°=55°
即∠2=55°。
12.26
【分析】两组对边分别平行且相等的四边形,叫做平行四边形;根据平行四边形相邻两边的长度是5厘米和8厘米可知,另外两条边的长度也是5厘米和8厘米,把平行四边形4条边长度相加,即可求出平行四边形周长。
【详解】5+8+5+8=26(厘米)
即一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是26厘米。
13.25×12=25×2+25×10
【分析】两位数乘两位数的竖式计算方法:先用下面因数个位的数去乘上面因数,得数的末位和下面因数的个位对齐,再用下面因数十位上的数去乘上面的因数,得数的末位和下面因数的十位对齐,然后把两次乘得的数加起来;乘法分配律:(a+b)×c=a×c+b×c,据此解答。
【详解】根据分析:将12分成了(2+10),再运用乘法分配律用25分别乘2、乘10,再相加;
25×12
=25×(2+10)
=25×2+25×10
=50+250
=300
所以列出相应的算式:25×12=25×2+25×10。
14. > = > >
【分析】720-35÷5中35÷5商是一位数,720减一个一位数还是三位数,720÷(3×5)中3×5积是两位数,720除以两位数商是两位数,据此判断。
76×12×5与76×(12×5)比较,运用了乘法结合律积不变。
75×(8+3)表示11个75相加,75×8+3表示8个75相加再加3,3个75比3大得多,据此比较。
960-(326-128)去括号后是960-326+128,再与960-326-128比较一个是加128,另一个是减128,据此比较。
【详解】720-35÷5(>)720÷(3×5)
76×12×5(=)76×(12×5)
75×(8+3)(>)75×8+3
960-(326-128)(>)960-326-128
15. 4848 96
【分析】算式的左边的因数中一个固定因数101,另一个因数是两位数;积是四位数,把第一个因数连续写两次即可得出答案。
【详解】12×101=1212
24×101=2424
36×101=3636
48×101=4848
96×101=9696
16.21
【分析】根据图形可知“一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人”,即每增加一张桌子,就多坐2人,由此可得规律:n张桌子可以坐下总人数=2+2n,据此解答。所以从44人中减去2人,再除以2就可以求出一共需要拼几张桌子。
【详解】(44-2)÷2
=42÷2
=21(张)
所以一共需要拼21张桌子。
17.①100;②5mn;③30a;④100
⑤64;⑥167;⑦9000;⑧128
【解析】略
18.20.34;17.79;18.64
【分析】小数加减法的运算方法是,先把小数点上下对齐,再按照整数加减法的计算方法进行计算,从低位加起,哪一位上的数相加满十,就向前一位进一;从低位减起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减;减法验算时,用减数加上差,看是不是等于被减数。
【详解】15.38+4.96=20.34 21.28-3.49=17.79
40.02-21.38=18.64
验算:
19.(1)58;(2)2400;
(3)7500;(4)6565
【分析】(1)根据除法的性质简算;
(2)把32化为4×8,再利用乘法交换律和乘法的结合律简算;
(3)、(4)根据乘法分配律简算。
【详解】(1)580÷5÷2
=580÷(5×2)
=580÷10
=58
(2)32×25×3
=4×8×25×3
=(4×25)×(8×3)
=100×(8×3)
=100×24
=2400
(3)34×75+67×75-75
=75×(34+67-1)
=75×(101-1)
=75×100
=7500
(4)65×101
=65×(100+1)
=65×100+65×1
=6500+65×1
=6500+65
=6565
20.61度
【分析】已知等腰三角形的顶角是58度,那么另外两个内角和是180-58=122度;再用122除以2,即可求出底角的度数。
【详解】(180-58)÷2
=122÷2
=61(度)
答:它的一个底角的度数是61度。
21.(1)(96-12b)吨
(2)36吨
【分析】(1)剩下的货物吨数=原有货物吨数-每车运的吨数×运的车数;
(2)将b=5代入字母表示的算式,求值即可。
【详解】(1)96-b×12=(96-12b)吨
答:仓库里剩下的货物吨数用式子表示为:(96-12b)吨。
(2)96-12b
=96-12×5
=96-60
=36(吨)
答:仓库里剩下的货物有36吨。
22.(1)(12m+8n)元
(2)16元
【分析】(1)分别算出青青购买樱桃和草莓的钱数,用单价×数量算出后再求和即可;
(2)将m=5,n=3代入(1)中算出具体花的钱,再用100减去就是应该找回的钱。
【详解】(1)樱桃:12×m=12m(元)
草莓:8×n=8n(元)
青青一共花的钱数:(12m+8n)元
答:青青一共花(12m+8n)元。
(2)当m=5,n=3时,
12m+8n
=12×5+8×3
=60+24
=84(元)
100-84=16(元)
答:应该找回16元。
23.2.017千米
【分析】根据题意,先用1.545+1.29求出泰山和衡山海拔高度的和,再减去0.818即可求出恒山的海拔高度是多少千米。
【详解】1.545+1.29-0.818
=2.835-0.818
=2.017(千米)
答:恒山的海拔高度是2.017千米。
24.(1)6.70元
(2)买一支钢笔、一个三角尺和一块橡皮一共需要多少钱?需要10.90元钱。
【分析】(1)根据小数减法的意义,用钢笔的价钱减去三角尺的价钱,再减去橡皮的价钱,即可求出一支钢笔比三角尺和橡皮多多少元;
(2)根据题目中所提供的信息,可以依据小数加法的意义,提出相关问题,再进行解答。
【详解】(1)8.80-1.60-0.50
=7.20-0.50
=6.70(元)
答:一支钢笔比三角尺和橡皮多6.70元。
(2)买一支钢笔、一个三角尺和一块橡皮一共需要多少钱?
8.80+1.60+0.50
=10.40+0.50
=10.90(元)
答:买一支钢笔、一个三角尺和一块橡皮一共需要10.90元钱。
【点睛】此题主要考查多位小数加减法的实际应用。
25.(1)第一小组的整体水平高
(2)见详解
【分析】(1)分别用小组颠球的总个数除以人数再进行比较即可;
(2)用增加同学颠球的个数和小组平均数进行比较,大于平均数整体水平提高;等于平均数整体水平不变;小于平均数整体水平下降。
【详解】(1)410÷5=82(个)
480÷6=80(个)
82个>80个
答:我认为第一小组的整体水平高一些。因为平均数可以代表这两个小组整体水平的高低。
(2)若6号同学的成绩小于82,那么第一组的整体水平会下降;
若6号同学的成绩等于82,那么第一组的整体水平没有变化;
若6号同学的成绩大于82,那么第一小组的整体水平会提高。
【点睛】明确平均数是颠球的总个数除以人数是解决本题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末高频考点检测卷(试题)2023-2024学年数学四年级下册青岛版
一、选择题
1.如图,幸福小区有一个花园,由3个大小不同的等边三角形组成。从甲地到乙地,下列说法错误的是( )。
A.①号路长60米 B.①号路和③号路一样长 C.②号路最短
2.已知△×○=16,下面选项正确的( )。
A.16÷○=△ B.△×16=○ C.○×16=△
3.李师傅每天做m个零件比刘师傅每天少做n个,刘师傅每天做( )个零件。
A.m+n B.m-n C.m-n+m
4.下面可以用式子5x+10表示的是( )。
A.一辆汽车每小时行驶x千米,这辆汽车5小时行驶的路程。
B.一个西瓜10元,一箱苹果x元,买5箱苹果和一个西瓜一共需要的钱数。
C.幼儿园有x个小朋友,每人分了5个面包,还剩下10个面包,一共分的面包数。
5.在一次百米赛跑中,前三名分别是甲(12.61秒)、乙(13.08秒)、丙(12.58秒),第一名是( )。
A.丙 B.乙 C.甲
6.在一组数据中,最大的一个数是67,最小的一个数是52,这组数据的平均数可能是( )。
A.68 B.59 C.52
7.下列选项中的三条线段能围成等腰三角形的是( )。
A.3cm、3cm、7cm B.2cm、3cm、4cm C.4cm、4cm、7cm
8.下面等式中只运用了乘法结合律的是( )。
A.5×6×4=3×4×10
B.(3×4)×8×5=3×(4×5)×8
C.4×(25×3)=(4×25)×3
二、填空题
9.丁丁今年a岁,妈妈今年b岁,那么15年以后妈妈比丁丁大( )岁。
10.一个正方形的边长是a米,它的周长是( )米,面积是( )平方米;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,正方形的面积是( )平方米。
11.已知∠1和∠2是直角三角形中的两个锐角。∠1=35°,∠2=( )°。
12.一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是( )厘米。
13.下面的竖式在计算过程中运用了乘法分配律,列出相应的算式:( )。
14.不计算,在括号里填上“>”“<”或“=”。
720-35÷5( )720÷(3×5)
76×12×5( )76×(12×5)
75×(8+3)( )75×8+3
960-(326-128)( )960-326-128
15.找规律,填一填。
12×101=1212
24×101=2424
36×101=3636
48×101=( )
( )×101=9696
16.光明小学三年级1班的学生组织聚餐,某餐馆有一种长方形桌子,每张桌子周围放4把椅子。如果客人多,就按照如图所示的方式拼桌。
三年级1班一共有44名同学,一共需要拼( )张桌子。
三、计算题
17.直接写得数。
①25×4= ②5×m×n= ③a×6×5= ④102=
⑤82= ⑥99+68= ⑦125×9×8= ⑧36+64-36+64=
18.用竖式计算。(带“※”的要验算)
15.38+4.96= 21.28-3.49= ※40.02-21.38=
19.用你喜欢的方法计算,能简算的一定要简算。
(1)580÷5÷2 (2)32×25×3
(3)34×75+67×75-75 (4)65×101
四、解答题
20.一个等腰三角形,它的顶角度数是58度。它的一个底角的度数是多少?
21.仓库里有货物96吨,运走了12车,每车运b吨。
(1)用式子表示仓库里剩下的吨数。
(2)利用这个式子,求当b=5时,仓库里剩下的货物有多少吨?
22.下面是青青在超市的购物情况
商品 数量(千克) 单价(元)
樱桃 m 12
草莓 n 8
(1)用含有字母的式子表示青青一共花的钱数。
(2)当m=5,n=3时,如果付给售货员100元,那么应找回多少元?
23.我国的“五岳”中,泰山海拔高度为1.545千米,衡山海拔高度为1.29千米,恒山的海拔高度比泰山和衡山海拔高度的和少0.818千米,恒山的海拔高度是多少千米?
24.看下表回答问题。
文具 单价(元)
钢笔 8.80
三角尺 1.60
橡皮 0.50
(1)一支钢笔比三角尺和橡皮多多少元?
(2)你还能提出什么问题?(解答)
25.下面是四年级一班两个小组的同学1分钟颠球比赛成绩记录表。
(1)你认为哪个小组颠球的整体水平高一些?请说明理由。
(2)如果第一组再增加一名学生参加比赛,你认为这名同学在规定时间内颠球个数可能是多少?此时第一组的整体水平会发生怎样的变化?请说明理由。
参考答案:
1.A
【分析】观察图形可知,①号路长(20+40+20+40)米;③号路长(2×40+2×20)米,从而对A和B作出判断;再求出②号路长(20+40)米,然后与①、②号路的长度进行比较,对C作出判断即可。
【详解】A.20+40+20+40
=60+20+40
=80+40
=120(米)
符合题意;
B.①号路长:
20+40+20+40
=60+60
=120(米)
③号路长:
2×40+2×20
=80+40
=120(米)
①号路和③号路一样长,不符合题意;
C.20+40=60(米)
60<120,所以②号路最短,不符合题意。
幸福小区有一个花园,由3个大小不同的等边三角形组成。从甲地到乙地,下列说法错误的是①号路长60米。
故答案为:A
2.A
【分析】乘数×乘数=积,积÷乘数=乘数。根据△×○=16,有○×△=16,16÷△=○,16÷○=△。
【详解】已知△×○=16,选项正确的是16÷○=△。
故答案为:A
3.A
【分析】根据题意刘师傅做的零件个数=李师傅做的零件个数+李师傅每天做零件比刘师傅每天少做n个,根据等量关系式代入法即可解答。
【详解】刘师傅每天做(m+n)个。
故答案为:A
4.B
【分析】根据路程=时间×速度,总价=单价×数量,分析每个选项,列式选出符合题意的即可。
【详解】A.一辆汽车每小时行驶x千米,这辆汽车5小时行驶的路程为5x千米,不符合题意;
B.买5箱苹果需要5x元,买5箱苹果和一个西瓜一共需要(5x+10)元,符合题意;
C.一共分了5x个面包,不符合题意。
可以用式子5x+10表示的是一个西瓜10元,一箱苹果x元,买5箱苹果和一个西瓜一共需要的钱数。
故答案为:B
5.A
【分析】小数大小的比较方法,先看小数的整数部分,整数部分大的这个数就大,整数部分相同的就看十分位,十分位大的这个数就大,十分位相同的就看百分位,百分位大的这个数就大……,据此判断出前三名同学用的时间的长短,然后根据路程一定时,谁用的时间越短,则谁的速度越快,据此解答即可。
【详解】12.58<12.61<13.08
根据分析得,这次百米赛跑前三名分别是丙(12.58秒)、甲(12.61秒)、乙(13.08秒),第一名是丙。
故答案为:A
6.B
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;其特点是比最大数小,比最小数大;依此选择。
【详解】A.68>67,因此这组数据的平均数不可能是68。
B.52<59<67,因此这组数据的平均数可能是59。
C.52=52,因此这组数据的平均数不可能是52。
这组数据的平均数可能是59。
故答案为:B
7.C
【分析】根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边才能构成三角形;等腰三角形有两条边相等。据此分析并选择即可。
【详解】A.3+3=6,6<7,这三条线段不能围成三角形;
B.2+3=5,5>4;这三条线段能围成三角形,但没有相等的边,不能围成等腰三角形;
C.4+4=8,8>7;这三条线段能围成三角形,并且有两条相等的边,能围成等腰三角形;
则三条线段能围成等腰三角形的是4cm、4cm、7cm。
故答案为:C
8.C
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。乘法交换律是指两个数相乘,交换乘数的位置,它们的积不变。据此逐项分析解答。
【详解】A.将6看成2×3,根据乘法交换律和乘法结合律可知:5×6×4=5×(2×3)×4=(5×2)×3×4=10×3×4=3×4×10,
B.(3×4)×8×5=3×(4×5)×8,先根据乘法交换律交换8和5的位置,再根据乘法结合律,先计算4×5。
C.4×(25×3)=(4×25)×3,根据乘法结合律,先计算4×25。乘数位置不变,没有运用乘法交换律。
只运用了乘法结合律的是4×(25×3)=(4×25)×3。
故答案为:C
9.b-a
【分析】两个人的年龄差是一个定数,不随时间的变化而变化,要求15年后妈妈比丁丁大多少岁,用妈妈今年的岁数减去丁丁今年的岁数,求出今年妈妈比丁丁大多少岁,也就是15年以后妈妈比丁丁大的岁数。
【详解】b-a
丁丁今年a岁,妈妈今年b岁,那么15年以后妈妈比丁丁大(b-a)岁。
10. 4a/4 a/4×a a2/a a c2/c c
【分析】正方形的周长=边长×4,正方形的面积=边长×边长。直接代入公式即可;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,那么这个正方形的边长是c米。再根据正方形的面积=边长×边长求解即可。
【详解】a×4=4a,a×a= a2,c×c= c2
一个正方形的边长是a米,它的周长是4a米,面积是a2平方米;如果从一个长是b米,宽是c米的长方形中,剪下一个最大的正方形,正方形的面积是c2平方米。
11.55
【分析】直角三角形中有一个直角,根据三角形的内角和为180°可知,∠2=180°-90°-∠1。
【详解】∠2=180°-90°-∠1=180°-90°-35°=55°
即∠2=55°。
12.26
【分析】两组对边分别平行且相等的四边形,叫做平行四边形;根据平行四边形相邻两边的长度是5厘米和8厘米可知,另外两条边的长度也是5厘米和8厘米,把平行四边形4条边长度相加,即可求出平行四边形周长。
【详解】5+8+5+8=26(厘米)
即一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是26厘米。
13.25×12=25×2+25×10
【分析】两位数乘两位数的竖式计算方法:先用下面因数个位的数去乘上面因数,得数的末位和下面因数的个位对齐,再用下面因数十位上的数去乘上面的因数,得数的末位和下面因数的十位对齐,然后把两次乘得的数加起来;乘法分配律:(a+b)×c=a×c+b×c,据此解答。
【详解】根据分析:将12分成了(2+10),再运用乘法分配律用25分别乘2、乘10,再相加;
25×12
=25×(2+10)
=25×2+25×10
=50+250
=300
所以列出相应的算式:25×12=25×2+25×10。
14. > = > >
【分析】720-35÷5中35÷5商是一位数,720减一个一位数还是三位数,720÷(3×5)中3×5积是两位数,720除以两位数商是两位数,据此判断。
76×12×5与76×(12×5)比较,运用了乘法结合律积不变。
75×(8+3)表示11个75相加,75×8+3表示8个75相加再加3,3个75比3大得多,据此比较。
960-(326-128)去括号后是960-326+128,再与960-326-128比较一个是加128,另一个是减128,据此比较。
【详解】720-35÷5(>)720÷(3×5)
76×12×5(=)76×(12×5)
75×(8+3)(>)75×8+3
960-(326-128)(>)960-326-128
15. 4848 96
【分析】算式的左边的因数中一个固定因数101,另一个因数是两位数;积是四位数,把第一个因数连续写两次即可得出答案。
【详解】12×101=1212
24×101=2424
36×101=3636
48×101=4848
96×101=9696
16.21
【分析】根据图形可知“一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人”,即每增加一张桌子,就多坐2人,由此可得规律:n张桌子可以坐下总人数=2+2n,据此解答。所以从44人中减去2人,再除以2就可以求出一共需要拼几张桌子。
【详解】(44-2)÷2
=42÷2
=21(张)
所以一共需要拼21张桌子。
17.①100;②5mn;③30a;④100
⑤64;⑥167;⑦9000;⑧128
【解析】略
18.20.34;17.79;18.64
【分析】小数加减法的运算方法是,先把小数点上下对齐,再按照整数加减法的计算方法进行计算,从低位加起,哪一位上的数相加满十,就向前一位进一;从低位减起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减;减法验算时,用减数加上差,看是不是等于被减数。
【详解】15.38+4.96=20.34 21.28-3.49=17.79
40.02-21.38=18.64
验算:
19.(1)58;(2)2400;
(3)7500;(4)6565
【分析】(1)根据除法的性质简算;
(2)把32化为4×8,再利用乘法交换律和乘法的结合律简算;
(3)、(4)根据乘法分配律简算。
【详解】(1)580÷5÷2
=580÷(5×2)
=580÷10
=58
(2)32×25×3
=4×8×25×3
=(4×25)×(8×3)
=100×(8×3)
=100×24
=2400
(3)34×75+67×75-75
=75×(34+67-1)
=75×(101-1)
=75×100
=7500
(4)65×101
=65×(100+1)
=65×100+65×1
=6500+65×1
=6500+65
=6565
20.61度
【分析】已知等腰三角形的顶角是58度,那么另外两个内角和是180-58=122度;再用122除以2,即可求出底角的度数。
【详解】(180-58)÷2
=122÷2
=61(度)
答:它的一个底角的度数是61度。
21.(1)(96-12b)吨
(2)36吨
【分析】(1)剩下的货物吨数=原有货物吨数-每车运的吨数×运的车数;
(2)将b=5代入字母表示的算式,求值即可。
【详解】(1)96-b×12=(96-12b)吨
答:仓库里剩下的货物吨数用式子表示为:(96-12b)吨。
(2)96-12b
=96-12×5
=96-60
=36(吨)
答:仓库里剩下的货物有36吨。
22.(1)(12m+8n)元
(2)16元
【分析】(1)分别算出青青购买樱桃和草莓的钱数,用单价×数量算出后再求和即可;
(2)将m=5,n=3代入(1)中算出具体花的钱,再用100减去就是应该找回的钱。
【详解】(1)樱桃:12×m=12m(元)
草莓:8×n=8n(元)
青青一共花的钱数:(12m+8n)元
答:青青一共花(12m+8n)元。
(2)当m=5,n=3时,
12m+8n
=12×5+8×3
=60+24
=84(元)
100-84=16(元)
答:应该找回16元。
23.2.017千米
【分析】根据题意,先用1.545+1.29求出泰山和衡山海拔高度的和,再减去0.818即可求出恒山的海拔高度是多少千米。
【详解】1.545+1.29-0.818
=2.835-0.818
=2.017(千米)
答:恒山的海拔高度是2.017千米。
24.(1)6.70元
(2)买一支钢笔、一个三角尺和一块橡皮一共需要多少钱?需要10.90元钱。
【分析】(1)根据小数减法的意义,用钢笔的价钱减去三角尺的价钱,再减去橡皮的价钱,即可求出一支钢笔比三角尺和橡皮多多少元;
(2)根据题目中所提供的信息,可以依据小数加法的意义,提出相关问题,再进行解答。
【详解】(1)8.80-1.60-0.50
=7.20-0.50
=6.70(元)
答:一支钢笔比三角尺和橡皮多6.70元。
(2)买一支钢笔、一个三角尺和一块橡皮一共需要多少钱?
8.80+1.60+0.50
=10.40+0.50
=10.90(元)
答:买一支钢笔、一个三角尺和一块橡皮一共需要10.90元钱。
【点睛】此题主要考查多位小数加减法的实际应用。
25.(1)第一小组的整体水平高
(2)见详解
【分析】(1)分别用小组颠球的总个数除以人数再进行比较即可;
(2)用增加同学颠球的个数和小组平均数进行比较,大于平均数整体水平提高;等于平均数整体水平不变;小于平均数整体水平下降。
【详解】(1)410÷5=82(个)
480÷6=80(个)
82个>80个
答:我认为第一小组的整体水平高一些。因为平均数可以代表这两个小组整体水平的高低。
(2)若6号同学的成绩小于82,那么第一组的整体水平会下降;
若6号同学的成绩等于82,那么第一组的整体水平没有变化;
若6号同学的成绩大于82,那么第一小组的整体水平会提高。
【点睛】明确平均数是颠球的总个数除以人数是解决本题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
