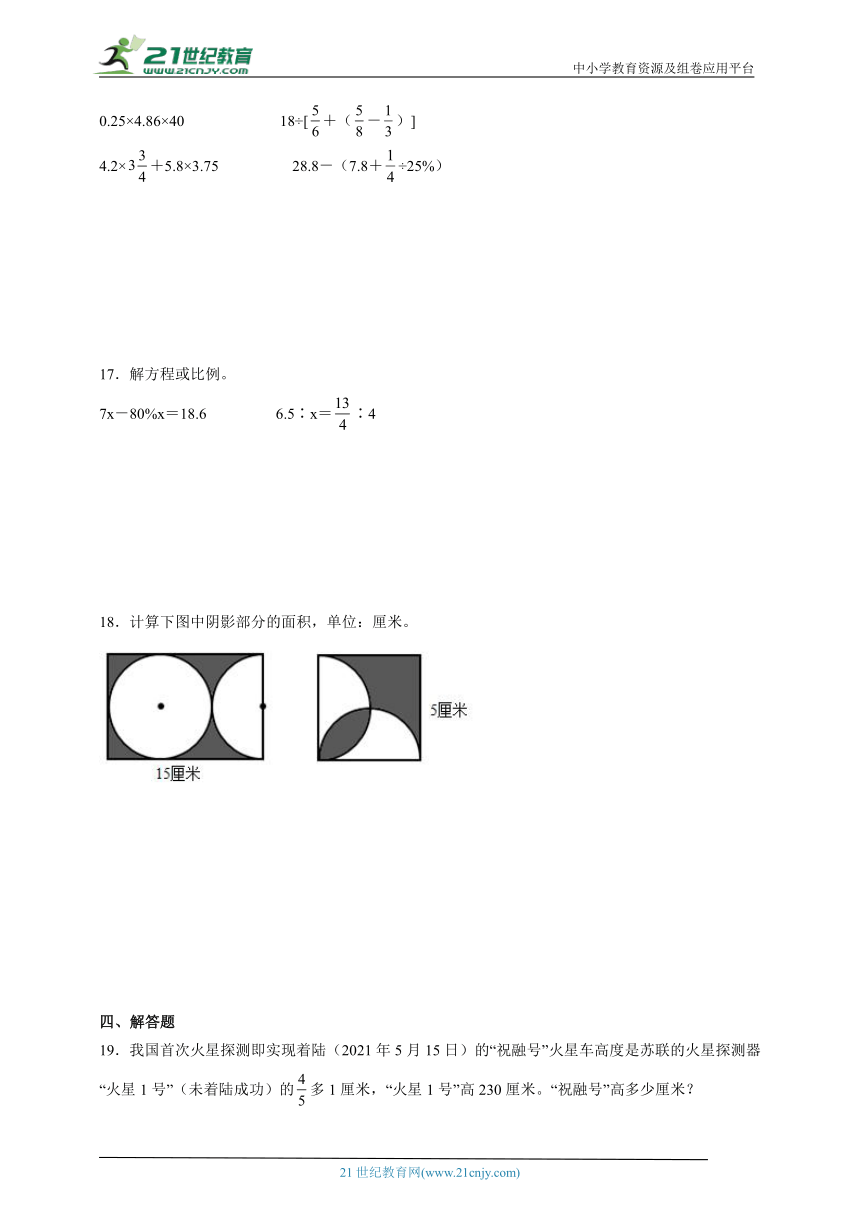
小升初高频考点检测卷(试题)2023-2024学年数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初高频考点检测卷(试题)2023-2024学年数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 607.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 06:07:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初高频考点检测卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.三个同学去打靶,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分;请估计这三人的平均成绩在( )。
A.90分以下 B.大于等于90分,小于等于93分之间
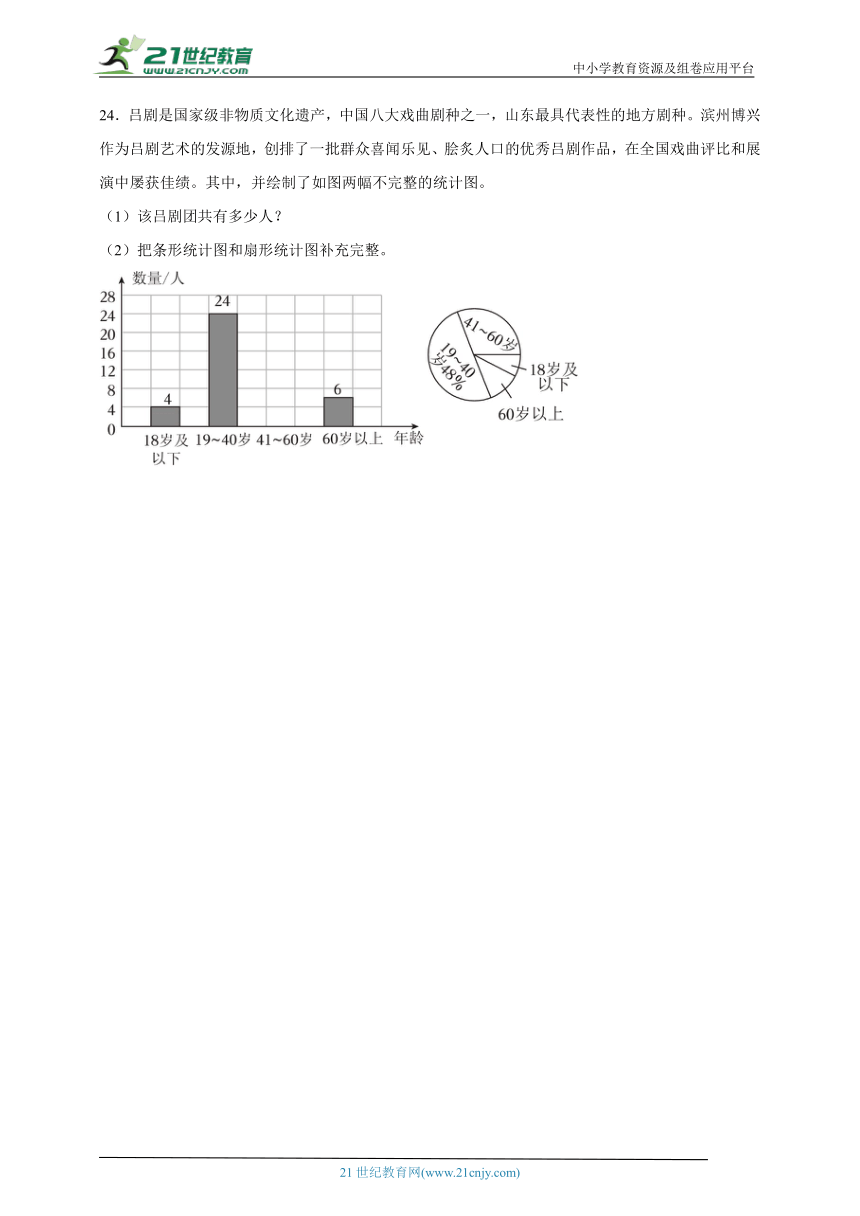
C.大于93分小于等于94分之间 D.94分以上
2.货车每次拉煤3吨,煤的总量和拉煤的次数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.下面的节日同在大月的一组是( )。
A.教师节,国庆节 B.妇女节,清明节
C.劳动节,建军节 D.元旦,儿童节
4.一项工程,甲队单独做要10天完成,乙队单独做要8天完成,甲队的工作效率比乙队慢( )。
A. B. C. D.
5.把四根绳子分别放在盒子里,露出来的部分一样长,这四根绳子中最长的是( )。
A. B.
C. D.
6.下图是六(1)、六(2)班同学参加学校“阳光体育节”活动的情况,两个班参加的总人数相等。下列说法错误的是( )。
A.六(1)班喜欢乒乓球的人数和六(2)班的一样多
B.六(1)班喜欢足球的人数比六(2)班的少
C.六(1)班喜欢羽毛球的人数比六(2)班的多
D.六(1)班喜欢篮球的人数比六(2)班的少
二、填空题
7.截至2022年6月12日,全国累计报告接种新冠病毒疫苗三十三亿八千九百四十五万四千剂次,横线上的数写作( ),四舍五入到亿位约是( )亿。
8.大年三十,小策一家在家庭群中抢红包。小策抢到了32.50元,手机屏幕显示为﹢32.50元,如果小策妈妈发了一个50元的红包,则显示为( )元。
9.在0.2∶1.6中,如果后项加上0.8,要使比值不变,前项应加上( )。
10.一种商品打八五折销售,“八五折”表示现价是原价的( )%。如果这种商品的原价是500元,现在便宜了( )元。
11.下面纸条的总长度是3米,涂色部分占全长的( ),空白部分的长是( )米。
12.一只箱子里装有一些大小完全相同的红、黄、蓝小球,其中有6个红球,4个黄球,如果摸到黄球的可能性是,那么箱子里有( ) 个蓝球。
13.有三根一模一样的小圆柱体,把它们头尾接在一起拼成了一个长为3dm的新圆柱体,此时表面积比原来减少了25.12dm2,这根新圆柱体的横截面的面积是( )dm2,它的体积是( )dm3。
14.如图,在长方形ABCD中,AB=8厘米,AD=6厘米,三角形ACE的面积是12平方厘米,那么梯形ABED的面积是( )平方厘米。
三、计算题
15.直接写出得数。
493×61≈ -= 8÷= 36×25%=
1%÷1%= ÷8= 0.25×0.8= 798÷204≈
16.能简便的要简算。
0.25×4.86×40 18÷[+(-)]
4.2×+5.8×3.75 28.8-(7.8+÷25%)
17.解方程或比例。
7x-80%x=18.6 6.5∶x=∶4
18.计算下图中阴影部分的面积,单位:厘米。
四、解答题
19.我国首次火星探测即实现着陆(2021年5月15日)的“祝融号”火星车高度是苏联的火星探测器“火星1号”(未着陆成功)的多1厘米,“火星1号”高230厘米。“祝融号”高多少厘米?
20.小明去西安兵马俑游玩,买了一个秦代将军模型(如图)。已知该人物模型的高度与实际高度的比是1∶10。请问这个将军俑的实际高度是多少米?(用比例知识解答)
21.一个长6分米,宽4分米,高10分米的长方体,里面放在一个底面积为18平方分米的圆锥体物体,在长方体容器内盛满水,再把物体拿出来后,水面高度是8分米,圆锥体物件的高度是多少分米?
22.如图中圆柱的底面周长是25.12cm,高是15dm,现用包装绳包扎,至少需要多长的包装绳?(接头处需15cm)
23.妈妈准备购买一台冰箱,看了两家商场同款冰箱的标价都是4400元,且两家商场都搞促销活动。A商场:家电一律八五折;B商场:每满500元返现金80元。妈妈应该选择哪家商场购买比较便宜?
24.吕剧是国家级非物质文化遗产,中国八大戏曲剧种之一,山东最具代表性的地方剧种。滨州博兴作为吕剧艺术的发源地,创排了一批群众喜闻乐见、脍炙人口的优秀吕剧作品,在全国戏曲评比和展演中屡获佳绩。其中,并绘制了如图两幅不完整的统计图。
(1)该吕剧团共有多少人?
(2)把条形统计图和扇形统计图补充完整。
参考答案:
1.C
【分析】根据条件“小华得了90分,小龙比小华成绩好,但不超过93分”可知,小龙可能得91分、92分,然后用总分数÷总份数=平均数,计算出三人的平均成绩,即可得到平均成绩的范围。
【详解】因为(99+90+91)÷3
=280÷3
=93.33
(99+90+92)÷3
=281÷3
≈93.67
所以这三人的平均成绩在大于93分小于等于94分之间。
故答案为:C
2.A
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】煤的总量÷货车拉煤的次数=每次拉煤的吨数(一定),则货车每次拉煤3吨,煤的总量和拉煤的次数成正比例。
故答案为:A
【点睛】此题属于辨识正反比例关系,就看这两个量是对应的比值一定,还是乘积一定,再做判断。
3.C
【分析】根据1、3、5、7、8、10、腊(12月),31天永不差,是大月,再确定各节日日期,做出选择即可。
【详解】A. 9月10日教师节,10月1日国庆节,9月是小月;
B. 3月8日妇女节,清明节在4月,4月是小月;
C. 5月1日劳动节,8月1日建军节,都是大月
D. 1月1日元旦,6月1日儿童节,6月是小月。
故答案为:C
【点睛】关键是熟悉各种节日的日期,区分大小月。
4.B
【分析】把这项工程的工作总量看作单位“1”,则甲队的工作效率是,乙队的工作效率是,用甲乙两队的工作效率差除以乙队的工作效率,可以计算出甲队的工作效率比乙队慢几分之几。
【详解】()÷
=
=
甲队的工作效率比乙队慢。
故答案为:B
【点睛】本题考查工程问题的解题方法,解题关键是要把工作总量看作单位“1”,利用甲乙两队的工作效率差除以乙队的工作效率,列式计算。
5.A
【分析】假设露出的绳子长1米,利用绳子的一部分的长度除以一部分所占的分率即可求出绳子的全长,再比较长短即可。
【详解】假设露出1米。
A.1÷=6(米)
B.1=2.5(米)
C.1=(米)
D.1=(米)
因为6>2.5>,所以最长。
故答案为:A
【点睛】本题考查了已知一个数的几分之几是多少的问题解答方法。
6.D
【分析】根据六(2)班的折线统计图中的数据,先用加法求出全班的总人数,因为两个班参加的总人数相等,所以也是六(1)班的总人数;把六(1)班的总人数看作单位“1”,结合六(1)班的扇形统计图,用总人数分别乘参加各类活动人数占总人数的百分比,求出六(1)班参加各类活动的人数,再与六(2)班参加相同活动的人数相比较,得出结论。
【详解】A.总人数:8+14+12+6=40(人)
六(2)班喜欢乒乓球的有6人;
六(1)班喜欢乒乓球的有:
40×15%
=40×0.15
=6(人)
六(1)班喜欢乒乓球的人数和六(2)班的一样多,原题说法正确;
B.六(2)班喜欢足球的有12人;
六(1)班喜欢足球的有:
40×15%
=40×0.15
=6(人)
6<12
六(1)班喜欢足球的人数比六(2)班的少,原题说法正确;
C.六(2)班喜欢羽毛球的有14人;
六(1)班喜欢羽毛球的有:
40×40%
=40×0.4
=16(人)
16>14
六(1)班喜欢羽毛球的人数比六(2)班的多,原题说法正确;
D.六(2)班喜欢篮球的有8人;
六(1)班喜欢篮球的有:
40×30%
=40×0.3
=12(人)
12>8
六(1)班喜欢篮球的人数比六(2)班的多,原题说法错误。
故答案为:D
【点睛】理解掌握折线统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的百分数问题。
7. 3389454000 34
【分析】整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出此数;四舍五入到亿位,把亿位后面千万位上的数进行四舍五入,再在数的末尾写上“亿”字,据此解答。
【详解】全国累计报告接种新冠病毒疫苗三十三亿八千九百四十五万四千剂次,横线上的数写作3389454000,四舍五入到亿位约是34亿。
【点睛】掌握整数的读写法和取近似数的方法是解答题目的关键。
8.﹣50
【分析】由题意可知,收入和支出是具有相反意义的量,收入用“﹢”表示,那么支出用“﹣”表示,小策收入32.50元记作﹢32.50元,则妈妈支出50元记作﹣50元。
【详解】小策抢到了32.50元,手机屏幕显示为﹢32.50元,如果小策妈妈发了一个50元的红包,则显示为﹣50元。
【点睛】本题主要考查正负数的意义及应用,找出相反意义的两种量是解答题目的关键。
9.0.1
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
0.2∶1.6的后项加上0.8得2.4,相当于后项乘1.5,根据比的基本性质,要使比值不变,前项也应乘1.5得0.3,由此确定前项应加上几。
【详解】(1.6+0.8)÷1.6
=2.4÷1.6
=1.5
0.2×1.5-0.2
=0.3-0.2
=0.1
在0.2∶1.6中,如果后项加上0.8,要使比值不变,前项应加上0.1。
【点睛】掌握比的基本性质及应用是解题的关键。
10. 85 75
【分析】把商品原价看作单位“1”,现价占原价的85%,则优惠的价格占原价的(1-85%),据此解答。
【详解】八五折=85%
500×(1-85%)
=500×0.15
=75(元)
所以,“八五折”表示现价是原价的85%,现在便宜了75元。
【点睛】几折就表示现价占原价的十分之几也就是百分之几十。
11.
【分析】求涂色部分占全长的几分之几,把整个长方形看作单位“1”,平均分的是单位“1”,表示把单位“1”平均分成5份,涂色部分占3份,用分数即可表示;空白部分占全长的(1-),求一个数的几分之几是多少,用乘法,用总长度3米乘空白部分占全长的分率,即可求出空白部分的长度。
【详解】1÷5×3
=×3
=
3×(1-)
=3×
=(米)
【点睛】解决此题关键是弄清求得是分率还是具体的数量,根据分数的意义以及分数乘法的意义求解。
12.10
【分析】已知摸到黄球的可能性是,黄球有4个,用黄球的数量除以,求出小球的总数量,减去红球和黄球的数量,即可求出蓝球的数量。
【详解】4÷=20(个)
20-6-4=10(个)
【点睛】解答此题应根据可能性的求法,根据分数除法的意义,求出小球的总数量是解题的关键。
13. 6.28 18.84
【分析】把3根相同的小圆柱体拼成1个大圆柱体,减少4个横截面的面积,根据减少部分的面积用除法求出新圆柱体底面的面积,最后利用“圆柱的体积=底面积×高”求出大圆柱体的体积,据此解答。
【详解】横截面的面积:25.12÷(2×2)
=25.12÷4
=6.28(dm2)
体积:6.28×3=18.84(dm3)
【点睛】本题主要考查立体图形的切拼,根据减少部分的面积求出圆柱的底面积并灵活运用圆柱的体积计算公式是解答题目的关键。
14.60
【分析】先依据三角形的面积公式:S=ah÷2,用12×2÷6即可求出三角形ACE中CE的长度,也就等于知道了梯形的下底,进而依据梯形的面积公式:S=(a+b)×h÷2,代入数据即可求解。
【详解】12×2÷6=4(厘米)
(8+4+8)×6÷2
=20×6÷2
=60(平方厘米)
这个梯形的面积是60平方厘米。
【点睛】此题主要考查三角形和梯形的面积公式的灵活应用。
15.30000;;10;9
1;;0.2;4
【详解】略
16.48.6;16
37.5;20
【分析】(1)根据乘法交换律a×b=b×a进行简算;
(2)先算小括号里面的减法,再算中括号里面的加法,最后算中括号外面的除法;
(3)把化成3.75,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
(4)先算括号里面的除法,再算括号里面的加法,最后算括号外面的减法。
【详解】(1)0.25×4.86×40
=0.25×40×4.86
=10×4.86
=48.6
(2)18÷[+(-)]
=18÷[+(-)]
=18÷[+]
=18÷
=18×
=16
(3)4.2×+5.8×3.75
=4.2×3.75+5.8×3.75
=(4.2+5.8)×3.75
=10×3.75
=37.5
(4)28.8-(7.8+÷25%)
=28.8-(7.8+0.25÷0.25)
=28.8-(7.8+1)
=28.8-8.8
=20
17.x=3;x=8
【分析】(1)先计算方程的左边,把原方程化为6.2x=18.6,再根据等式的性质,在方程两边同时除以6.2即可;
(2)根据比例的基本性质,化比例式为方程式x=6.5×4,然后根据等式的性质,在方程两边同时除以即可。
【详解】7x-80%x=18.6
解:6.2x=18.6
6.2x÷6.2=18.6÷6.2
x=3
6.5∶x=∶4
解:x=6.5×4
x÷=6.5×4÷
x=26÷
x=26×
x=8
18.32.25平方厘米;12.5平方厘米
【分析】(1)由图意可知,长方形的长是15厘米,宽是长的,圆的半径是长方形的宽,图中阴影部分的面积=长方形的面积-一个圆的面积-一个半圆的面积;圆的面积公式:S=πr2,据此计算;
(2)如下图:把两个半圆重叠的部分移到红区,可知阴影部分的面积等于正方形的面积的一半;正方形的面积=边长×边长,据此计算。
【详解】(1)15×=10(厘米)
15×10-3.14×(10÷2)2-3.14×(10÷2)2×
=150-3.14×25-3.14×25×
=150-78.5-39.25
=71.5-39.25
=32.25(平方厘米)
(2)5×5÷2
=25÷2
=12.5(平方厘米)
19.185厘米
【分析】把“火星1号”高度看作单位“1”,“火星1号”高度×+1=“祝融号”高度,据此解答。
【详解】230×+1
=184+1
=185(厘米)
答:“祝融号”高185厘米。
【点睛】此题主要考查了分数乘法的应用,明确求一个数的几分之几用乘法。
20.1.95米
【分析】已知人物模型高19.5厘米,根据该人物模型的高度与实际高度的比是1∶10,据此列出比例方程,并求解。注意单位的换算:1米=100厘米。
【详解】解:这个将军俑的实际高度是厘米。
19.5∶=1∶10
×1=19.5×10
=195
195厘米=1.95米
答:这个将军俑的实际高度是1.95米。
【点睛】本题考查列比例方程解决实际问题,设出所求量,根据模型的高度与实际高度的比列出比例方程。
21.8分米
【分析】由题意可知:这个圆锥的体积等于长方体容器内水下降的体积,首先根据长方体的体积公式:V=abh,求出容器中水下降的体积(圆锥的体积),再根据圆锥的体积公式:V=Sh,用圆锥的体积除以除以圆锥的底面积即可求出圆锥的高。
【详解】6×4×(10-8)18
=24×2×3÷18
=144÷18
=8(分米)
答:圆锥物体的高是8分米。
【点睛】此题解答根据是理解:这个圆锥的体积等于长方体容器内水下降的体积,求出圆锥的体积,再利用圆锥的体积公式求出它的高即可。
22.647厘米
【分析】根据题意和图形可知,所需彩带的长度等于4条高,4条直径,再加打结处用的15厘米,由此列式解答。
【详解】15分米=150厘米
底面直径:
25.12÷3.14=8(厘米)
8×4+150×4+15
=32+600+15
=647(厘米)
答:至少需要647厘米的包装绳。
【点睛】此题属于圆柱体知识的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些数据的长度和。
23.A商场
【分析】计算两种商场购买冰箱的价格,再进行比较即可。
【详解】A商场:4400×85%=3740(元)
B商场:500×8=4000(元)
4400元里有8个500元,返8个80元。
4400-8×80
=4400-360
=4040(元)
3740<4040
答:妈妈应该选择A商场购买比较便宜。
【点睛】本题考查折扣问题,解答本题的关键是先计算两种商场购买所需价格。
24.(1)50人;
(2)见详解。
【分析】(1)根据题意,用19到40岁的人数24除以19到40岁所占百分数48%就得总人数。
(2)分别用4和6除以总人数就得18岁及以下和60岁以上所占百分数,再用100%减去已知的18岁及以下、60岁以上、19到40岁所占百分数,求出41到60岁所占的百分数。根据总数乘百分数求得41岁到60岁的人数,然后作图即可。
【详解】(1)24÷48%
=24÷0.48
=50(人)
答:吕剧团共有50人。
(2)18岁及以下所占百分比:4÷50=8%
60岁以上所占百分比:6÷50=12%
41到60岁所占在分比:1-8%-12%-48%
=92%-12%-48%
=80%-48%
=32%
41到60岁的人数:50×32%=16(人)
如下图:
【点睛】本题考查了学生对扇形统计图与条形统计图意义的掌握,结合题意解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初高频考点检测卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.三个同学去打靶,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分;请估计这三人的平均成绩在( )。
A.90分以下 B.大于等于90分,小于等于93分之间
C.大于93分小于等于94分之间 D.94分以上
2.货车每次拉煤3吨,煤的总量和拉煤的次数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.下面的节日同在大月的一组是( )。
A.教师节,国庆节 B.妇女节,清明节
C.劳动节,建军节 D.元旦,儿童节
4.一项工程,甲队单独做要10天完成,乙队单独做要8天完成,甲队的工作效率比乙队慢( )。
A. B. C. D.
5.把四根绳子分别放在盒子里,露出来的部分一样长,这四根绳子中最长的是( )。
A. B.
C. D.
6.下图是六(1)、六(2)班同学参加学校“阳光体育节”活动的情况,两个班参加的总人数相等。下列说法错误的是( )。
A.六(1)班喜欢乒乓球的人数和六(2)班的一样多
B.六(1)班喜欢足球的人数比六(2)班的少
C.六(1)班喜欢羽毛球的人数比六(2)班的多
D.六(1)班喜欢篮球的人数比六(2)班的少
二、填空题
7.截至2022年6月12日,全国累计报告接种新冠病毒疫苗三十三亿八千九百四十五万四千剂次,横线上的数写作( ),四舍五入到亿位约是( )亿。
8.大年三十,小策一家在家庭群中抢红包。小策抢到了32.50元,手机屏幕显示为﹢32.50元,如果小策妈妈发了一个50元的红包,则显示为( )元。
9.在0.2∶1.6中,如果后项加上0.8,要使比值不变,前项应加上( )。
10.一种商品打八五折销售,“八五折”表示现价是原价的( )%。如果这种商品的原价是500元,现在便宜了( )元。
11.下面纸条的总长度是3米,涂色部分占全长的( ),空白部分的长是( )米。
12.一只箱子里装有一些大小完全相同的红、黄、蓝小球,其中有6个红球,4个黄球,如果摸到黄球的可能性是,那么箱子里有( ) 个蓝球。
13.有三根一模一样的小圆柱体,把它们头尾接在一起拼成了一个长为3dm的新圆柱体,此时表面积比原来减少了25.12dm2,这根新圆柱体的横截面的面积是( )dm2,它的体积是( )dm3。
14.如图,在长方形ABCD中,AB=8厘米,AD=6厘米,三角形ACE的面积是12平方厘米,那么梯形ABED的面积是( )平方厘米。
三、计算题
15.直接写出得数。
493×61≈ -= 8÷= 36×25%=
1%÷1%= ÷8= 0.25×0.8= 798÷204≈
16.能简便的要简算。
0.25×4.86×40 18÷[+(-)]
4.2×+5.8×3.75 28.8-(7.8+÷25%)
17.解方程或比例。
7x-80%x=18.6 6.5∶x=∶4
18.计算下图中阴影部分的面积,单位:厘米。
四、解答题
19.我国首次火星探测即实现着陆(2021年5月15日)的“祝融号”火星车高度是苏联的火星探测器“火星1号”(未着陆成功)的多1厘米,“火星1号”高230厘米。“祝融号”高多少厘米?
20.小明去西安兵马俑游玩,买了一个秦代将军模型(如图)。已知该人物模型的高度与实际高度的比是1∶10。请问这个将军俑的实际高度是多少米?(用比例知识解答)
21.一个长6分米,宽4分米,高10分米的长方体,里面放在一个底面积为18平方分米的圆锥体物体,在长方体容器内盛满水,再把物体拿出来后,水面高度是8分米,圆锥体物件的高度是多少分米?
22.如图中圆柱的底面周长是25.12cm,高是15dm,现用包装绳包扎,至少需要多长的包装绳?(接头处需15cm)
23.妈妈准备购买一台冰箱,看了两家商场同款冰箱的标价都是4400元,且两家商场都搞促销活动。A商场:家电一律八五折;B商场:每满500元返现金80元。妈妈应该选择哪家商场购买比较便宜?
24.吕剧是国家级非物质文化遗产,中国八大戏曲剧种之一,山东最具代表性的地方剧种。滨州博兴作为吕剧艺术的发源地,创排了一批群众喜闻乐见、脍炙人口的优秀吕剧作品,在全国戏曲评比和展演中屡获佳绩。其中,并绘制了如图两幅不完整的统计图。
(1)该吕剧团共有多少人?
(2)把条形统计图和扇形统计图补充完整。
参考答案:
1.C
【分析】根据条件“小华得了90分,小龙比小华成绩好,但不超过93分”可知,小龙可能得91分、92分,然后用总分数÷总份数=平均数,计算出三人的平均成绩,即可得到平均成绩的范围。
【详解】因为(99+90+91)÷3
=280÷3
=93.33
(99+90+92)÷3
=281÷3
≈93.67
所以这三人的平均成绩在大于93分小于等于94分之间。
故答案为:C
2.A
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】煤的总量÷货车拉煤的次数=每次拉煤的吨数(一定),则货车每次拉煤3吨,煤的总量和拉煤的次数成正比例。
故答案为:A
【点睛】此题属于辨识正反比例关系,就看这两个量是对应的比值一定,还是乘积一定,再做判断。
3.C
【分析】根据1、3、5、7、8、10、腊(12月),31天永不差,是大月,再确定各节日日期,做出选择即可。
【详解】A. 9月10日教师节,10月1日国庆节,9月是小月;
B. 3月8日妇女节,清明节在4月,4月是小月;
C. 5月1日劳动节,8月1日建军节,都是大月
D. 1月1日元旦,6月1日儿童节,6月是小月。
故答案为:C
【点睛】关键是熟悉各种节日的日期,区分大小月。
4.B
【分析】把这项工程的工作总量看作单位“1”,则甲队的工作效率是,乙队的工作效率是,用甲乙两队的工作效率差除以乙队的工作效率,可以计算出甲队的工作效率比乙队慢几分之几。
【详解】()÷
=
=
甲队的工作效率比乙队慢。
故答案为:B
【点睛】本题考查工程问题的解题方法,解题关键是要把工作总量看作单位“1”,利用甲乙两队的工作效率差除以乙队的工作效率,列式计算。
5.A
【分析】假设露出的绳子长1米,利用绳子的一部分的长度除以一部分所占的分率即可求出绳子的全长,再比较长短即可。
【详解】假设露出1米。
A.1÷=6(米)
B.1=2.5(米)
C.1=(米)
D.1=(米)
因为6>2.5>,所以最长。
故答案为:A
【点睛】本题考查了已知一个数的几分之几是多少的问题解答方法。
6.D
【分析】根据六(2)班的折线统计图中的数据,先用加法求出全班的总人数,因为两个班参加的总人数相等,所以也是六(1)班的总人数;把六(1)班的总人数看作单位“1”,结合六(1)班的扇形统计图,用总人数分别乘参加各类活动人数占总人数的百分比,求出六(1)班参加各类活动的人数,再与六(2)班参加相同活动的人数相比较,得出结论。
【详解】A.总人数:8+14+12+6=40(人)
六(2)班喜欢乒乓球的有6人;
六(1)班喜欢乒乓球的有:
40×15%
=40×0.15
=6(人)
六(1)班喜欢乒乓球的人数和六(2)班的一样多,原题说法正确;
B.六(2)班喜欢足球的有12人;
六(1)班喜欢足球的有:
40×15%
=40×0.15
=6(人)
6<12
六(1)班喜欢足球的人数比六(2)班的少,原题说法正确;
C.六(2)班喜欢羽毛球的有14人;
六(1)班喜欢羽毛球的有:
40×40%
=40×0.4
=16(人)
16>14
六(1)班喜欢羽毛球的人数比六(2)班的多,原题说法正确;
D.六(2)班喜欢篮球的有8人;
六(1)班喜欢篮球的有:
40×30%
=40×0.3
=12(人)
12>8
六(1)班喜欢篮球的人数比六(2)班的多,原题说法错误。
故答案为:D
【点睛】理解掌握折线统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的百分数问题。
7. 3389454000 34
【分析】整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出此数;四舍五入到亿位,把亿位后面千万位上的数进行四舍五入,再在数的末尾写上“亿”字,据此解答。
【详解】全国累计报告接种新冠病毒疫苗三十三亿八千九百四十五万四千剂次,横线上的数写作3389454000,四舍五入到亿位约是34亿。
【点睛】掌握整数的读写法和取近似数的方法是解答题目的关键。
8.﹣50
【分析】由题意可知,收入和支出是具有相反意义的量,收入用“﹢”表示,那么支出用“﹣”表示,小策收入32.50元记作﹢32.50元,则妈妈支出50元记作﹣50元。
【详解】小策抢到了32.50元,手机屏幕显示为﹢32.50元,如果小策妈妈发了一个50元的红包,则显示为﹣50元。
【点睛】本题主要考查正负数的意义及应用,找出相反意义的两种量是解答题目的关键。
9.0.1
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
0.2∶1.6的后项加上0.8得2.4,相当于后项乘1.5,根据比的基本性质,要使比值不变,前项也应乘1.5得0.3,由此确定前项应加上几。
【详解】(1.6+0.8)÷1.6
=2.4÷1.6
=1.5
0.2×1.5-0.2
=0.3-0.2
=0.1
在0.2∶1.6中,如果后项加上0.8,要使比值不变,前项应加上0.1。
【点睛】掌握比的基本性质及应用是解题的关键。
10. 85 75
【分析】把商品原价看作单位“1”,现价占原价的85%,则优惠的价格占原价的(1-85%),据此解答。
【详解】八五折=85%
500×(1-85%)
=500×0.15
=75(元)
所以,“八五折”表示现价是原价的85%,现在便宜了75元。
【点睛】几折就表示现价占原价的十分之几也就是百分之几十。
11.
【分析】求涂色部分占全长的几分之几,把整个长方形看作单位“1”,平均分的是单位“1”,表示把单位“1”平均分成5份,涂色部分占3份,用分数即可表示;空白部分占全长的(1-),求一个数的几分之几是多少,用乘法,用总长度3米乘空白部分占全长的分率,即可求出空白部分的长度。
【详解】1÷5×3
=×3
=
3×(1-)
=3×
=(米)
【点睛】解决此题关键是弄清求得是分率还是具体的数量,根据分数的意义以及分数乘法的意义求解。
12.10
【分析】已知摸到黄球的可能性是,黄球有4个,用黄球的数量除以,求出小球的总数量,减去红球和黄球的数量,即可求出蓝球的数量。
【详解】4÷=20(个)
20-6-4=10(个)
【点睛】解答此题应根据可能性的求法,根据分数除法的意义,求出小球的总数量是解题的关键。
13. 6.28 18.84
【分析】把3根相同的小圆柱体拼成1个大圆柱体,减少4个横截面的面积,根据减少部分的面积用除法求出新圆柱体底面的面积,最后利用“圆柱的体积=底面积×高”求出大圆柱体的体积,据此解答。
【详解】横截面的面积:25.12÷(2×2)
=25.12÷4
=6.28(dm2)
体积:6.28×3=18.84(dm3)
【点睛】本题主要考查立体图形的切拼,根据减少部分的面积求出圆柱的底面积并灵活运用圆柱的体积计算公式是解答题目的关键。
14.60
【分析】先依据三角形的面积公式:S=ah÷2,用12×2÷6即可求出三角形ACE中CE的长度,也就等于知道了梯形的下底,进而依据梯形的面积公式:S=(a+b)×h÷2,代入数据即可求解。
【详解】12×2÷6=4(厘米)
(8+4+8)×6÷2
=20×6÷2
=60(平方厘米)
这个梯形的面积是60平方厘米。
【点睛】此题主要考查三角形和梯形的面积公式的灵活应用。
15.30000;;10;9
1;;0.2;4
【详解】略
16.48.6;16
37.5;20
【分析】(1)根据乘法交换律a×b=b×a进行简算;
(2)先算小括号里面的减法,再算中括号里面的加法,最后算中括号外面的除法;
(3)把化成3.75,然后根据乘法分配律a×c+b×c=(a+b)×c进行简算;
(4)先算括号里面的除法,再算括号里面的加法,最后算括号外面的减法。
【详解】(1)0.25×4.86×40
=0.25×40×4.86
=10×4.86
=48.6
(2)18÷[+(-)]
=18÷[+(-)]
=18÷[+]
=18÷
=18×
=16
(3)4.2×+5.8×3.75
=4.2×3.75+5.8×3.75
=(4.2+5.8)×3.75
=10×3.75
=37.5
(4)28.8-(7.8+÷25%)
=28.8-(7.8+0.25÷0.25)
=28.8-(7.8+1)
=28.8-8.8
=20
17.x=3;x=8
【分析】(1)先计算方程的左边,把原方程化为6.2x=18.6,再根据等式的性质,在方程两边同时除以6.2即可;
(2)根据比例的基本性质,化比例式为方程式x=6.5×4,然后根据等式的性质,在方程两边同时除以即可。
【详解】7x-80%x=18.6
解:6.2x=18.6
6.2x÷6.2=18.6÷6.2
x=3
6.5∶x=∶4
解:x=6.5×4
x÷=6.5×4÷
x=26÷
x=26×
x=8
18.32.25平方厘米;12.5平方厘米
【分析】(1)由图意可知,长方形的长是15厘米,宽是长的,圆的半径是长方形的宽,图中阴影部分的面积=长方形的面积-一个圆的面积-一个半圆的面积;圆的面积公式:S=πr2,据此计算;
(2)如下图:把两个半圆重叠的部分移到红区,可知阴影部分的面积等于正方形的面积的一半;正方形的面积=边长×边长,据此计算。
【详解】(1)15×=10(厘米)
15×10-3.14×(10÷2)2-3.14×(10÷2)2×
=150-3.14×25-3.14×25×
=150-78.5-39.25
=71.5-39.25
=32.25(平方厘米)
(2)5×5÷2
=25÷2
=12.5(平方厘米)
19.185厘米
【分析】把“火星1号”高度看作单位“1”,“火星1号”高度×+1=“祝融号”高度,据此解答。
【详解】230×+1
=184+1
=185(厘米)
答:“祝融号”高185厘米。
【点睛】此题主要考查了分数乘法的应用,明确求一个数的几分之几用乘法。
20.1.95米
【分析】已知人物模型高19.5厘米,根据该人物模型的高度与实际高度的比是1∶10,据此列出比例方程,并求解。注意单位的换算:1米=100厘米。
【详解】解:这个将军俑的实际高度是厘米。
19.5∶=1∶10
×1=19.5×10
=195
195厘米=1.95米
答:这个将军俑的实际高度是1.95米。
【点睛】本题考查列比例方程解决实际问题,设出所求量,根据模型的高度与实际高度的比列出比例方程。
21.8分米
【分析】由题意可知:这个圆锥的体积等于长方体容器内水下降的体积,首先根据长方体的体积公式:V=abh,求出容器中水下降的体积(圆锥的体积),再根据圆锥的体积公式:V=Sh,用圆锥的体积除以除以圆锥的底面积即可求出圆锥的高。
【详解】6×4×(10-8)18
=24×2×3÷18
=144÷18
=8(分米)
答:圆锥物体的高是8分米。
【点睛】此题解答根据是理解:这个圆锥的体积等于长方体容器内水下降的体积,求出圆锥的体积,再利用圆锥的体积公式求出它的高即可。
22.647厘米
【分析】根据题意和图形可知,所需彩带的长度等于4条高,4条直径,再加打结处用的15厘米,由此列式解答。
【详解】15分米=150厘米
底面直径:
25.12÷3.14=8(厘米)
8×4+150×4+15
=32+600+15
=647(厘米)
答:至少需要647厘米的包装绳。
【点睛】此题属于圆柱体知识的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些数据的长度和。
23.A商场
【分析】计算两种商场购买冰箱的价格,再进行比较即可。
【详解】A商场:4400×85%=3740(元)
B商场:500×8=4000(元)
4400元里有8个500元,返8个80元。
4400-8×80
=4400-360
=4040(元)
3740<4040
答:妈妈应该选择A商场购买比较便宜。
【点睛】本题考查折扣问题,解答本题的关键是先计算两种商场购买所需价格。
24.(1)50人;
(2)见详解。
【分析】(1)根据题意,用19到40岁的人数24除以19到40岁所占百分数48%就得总人数。
(2)分别用4和6除以总人数就得18岁及以下和60岁以上所占百分数,再用100%减去已知的18岁及以下、60岁以上、19到40岁所占百分数,求出41到60岁所占的百分数。根据总数乘百分数求得41岁到60岁的人数,然后作图即可。
【详解】(1)24÷48%
=24÷0.48
=50(人)
答:吕剧团共有50人。
(2)18岁及以下所占百分比:4÷50=8%
60岁以上所占百分比:6÷50=12%
41到60岁所占在分比:1-8%-12%-48%
=92%-12%-48%
=80%-48%
=32%
41到60岁的人数:50×32%=16(人)
如下图:
【点睛】本题考查了学生对扇形统计图与条形统计图意义的掌握,结合题意解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
