2023~2024学年广东广州天河区高三上学期期中数学试卷(实验学校质量检测)(PDF版含解析)
文档属性
| 名称 | 2023~2024学年广东广州天河区高三上学期期中数学试卷(实验学校质量检测)(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 00:00:00 | ||
图片预览




文档简介
2023~2024学年广东广州天河区高三上学期期中数学试卷(实验学校质量
检测)
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 ( )
A.
B.
C.R
D.
2、使“ ”成立的一个充分不必要条件是( )
A.
B.
C.
D.
3、已知圆锥的侧面积(单位: )为 ,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:
)是( )
A.
B.
C.
D.
4、若 为等差数列, 是其前 项的和,且 为等比数列, ,则 的
值为( )
A.
B.
C.
D.
5、已知双曲线 的右焦点为 ,以 为圆心, 为半径的圆与双曲线的一条渐近线的
两个交点为 .若 ,则该双曲线的离心率为( )
A.
B.
C.
D.
6、将函数 在 上单调递增,则 的最大值为( )
A.
B.
C.
D.
7、设函数 是奇函数 的导函数, ,当 时, ,则不等式
的解集为( )
A.
B.
C.
D.
8、 中, 为 上一点且满足 ,若 为 上一点,且满足 为正实
数,则下列结论正确的是( )
A. 的最小值为
B. 的最大值为1
C. 的最小值为4
D. 的最大值为16
二、多选题(本大题共4小题,每小题5分,共20分)
9、已知i为虚数单位,下列说法正确的是( )
i
A.若复数 ,则
i
B.若复数z满足 i ,则复平面内z对应的点Z在一条直线上
C.若 i是纯虚数,则实数
D.复数 i的虚部为 i
10、已知过点A(a,0)作曲线 的切线有且仅有两条,则实数a的值可以是( )
A.-2
B.4
C.0
D.6
11、已知 是抛物线 的焦点, 是 上的两点, 为原点,则( )
A.若 垂直 的准线于点 ,且 ,则四边形 的周长为
B.若 ,则 的面积为
C.若直线 过点 ,则 的最小值为
D.若 ,则直线 恒过定点
12、如图,矩形 中, 为边 的中点,沿 将 折起,点 折至 处 平
面 分别在线段 和侧面 上运动,且 ,若 分别为线段 的中点,则在
折起过程中,下列说法正确的是( )
A. 面积的最大值为
B.存在某个位置,使得
C.三棱锥 体积最大时,三棱锥 的外接球的表面积为
D.三棱锥 体积最大时,点 到平面 的距离的最小值为 .
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知向量 ,则向量 在向量 上的投影向量的坐标为 .
14、已知函数 .若 ,则 .
15、已知函数 ,若 ,则实数 的取值范围为 .
16、如图,矩形 中, 分别为线段 上的动点,且满足
.点 关于原点的对称点为 ,直线 与 交于点 ,则点 到直线
的最小距离为 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知等比数列 的第二 三 四项分别是等差数列 的第二 五 十四项,且等差数列 的首项 ,公
差 .
(1)求数列 与 的通项公式;
(2)设数列 对任意 均有 成立,求 的值.
18、(本小题12分)
在锐角 中,内角 的对边分别为 ,已知 .
(1)求 ;
(2)若 ,求 的取值范围.
19、(本小题12分)
如图,在三棱柱 中, 为等边三角形,四边形 是边长为 的正方形, 为 中
点,且 .
(1)、求证: 平面 ;
(2)、若点 在线段 上,且直线 与平面 所成角的正弦值为 ,求点 到平面 的距离.
20、(本小题12分)
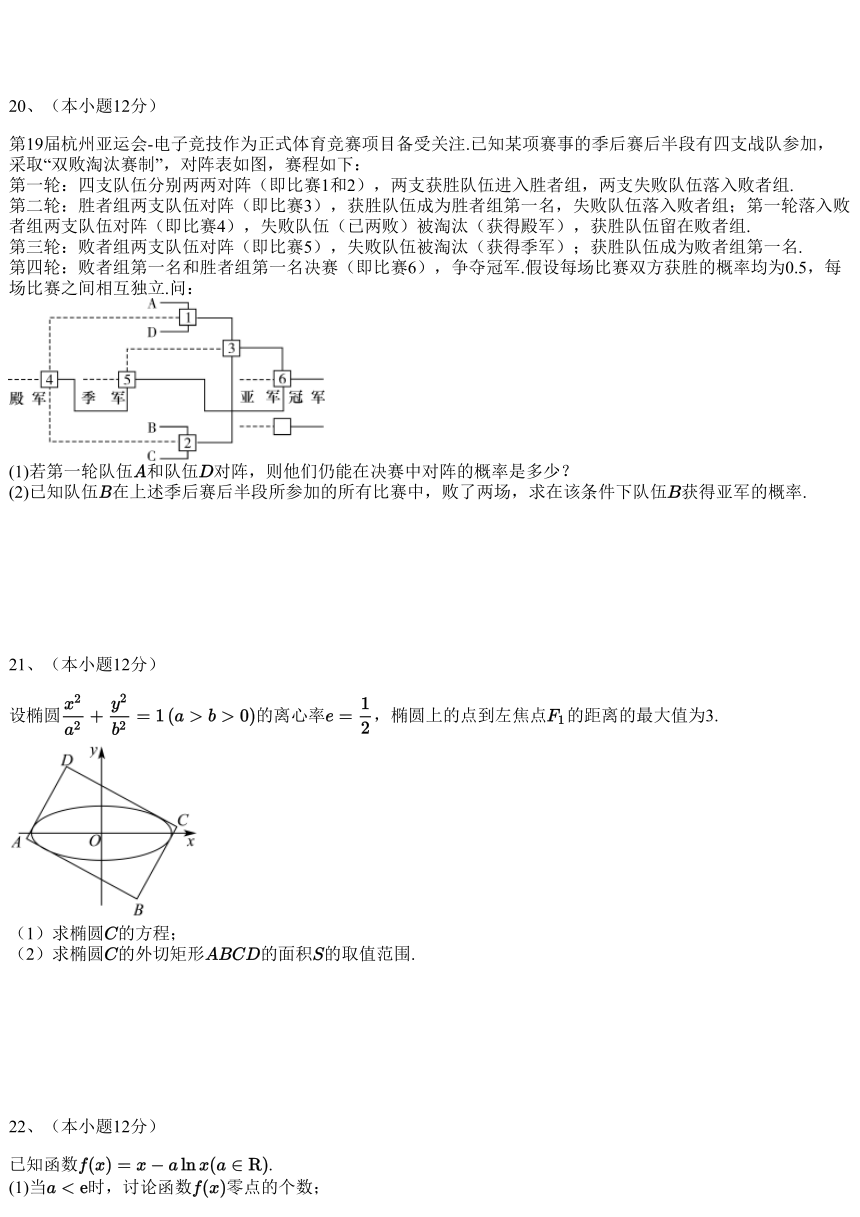
第19届杭州亚运会-电子竞技作为正式体育竞赛项目备受关注.已知某项赛事的季后赛后半段有四支战队参加,
采取“双败淘汰赛制”,对阵表如图,赛程如下:
第一轮:四支队伍分别两两对阵(即比赛1和2) ,两支获胜队伍进入胜者组,两支失败队伍落入败者组.
第二轮:胜者组两支队伍对阵(即比赛3),获胜队伍成为胜者组第一名,失败队伍落入败者组;第一轮 落入败
者组两支队伍对阵(即比赛4),失败队伍(已两败)被淘汰(获得殿军),获胜队伍留在败者组.
第三轮:败者组两支队伍对阵(即比赛5),失败队伍被淘汰(获得季军);获胜队伍成为败者组第 一名.
第四轮:败者组第一名和胜者组第一名决赛(即比赛6),争夺冠军.假设每场比赛双方获胜的概率均为0.5 ,每
场比赛之间相互独立.问:
(1)若第一轮队伍 和队伍 对阵,则他们仍能在决赛中对阵的概率是多少?
(2)已知队伍 在上述季后赛后半段所参加的所有比赛中,败了两场,求在该 条件下队伍 获得亚军的概率.
21、(本小题12分)
设椭圆 的离心率 ,椭圆上的点到左焦点 的距离的最大值为3.
(1)求椭圆 的方程;
(2)求椭圆 的外切矩形 的面积 的取值范围.
22、(本小题12分)
已知函数 .
(1)当 时,讨论函数 零点的 个数;
(2)当 时, 恒成立,求 的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
求出函数的定义域和值域,可分别化简集合 , ,再利用交集的定义求解即可.
依题意: , ,
所以 .
故选:A.
2、
【答 案】
D
【分析】
根据充分不必要条件的意思和不等式的性质可得答案.
只有当 同号时才有 ,故 错,
,故B错,
推不出 显然错 误,
,而反之不成立 ,故D满足题意,
故选:D.
3、
【答 案】
B
【分析】
利用扇形的面积公式 ,底面圆周长等于扇形弧长 ,即得解.
设圆锥底面半径为 ,母线长为 ,则
,解得 .
故选:B
4、
【答 案】
D
【分析】
根据等差数列以及等比数列的性质分别求得 的值,结合三角函数诱导公式化简求值,即得答案.
因为 为等差数列,故 ,
所以 ,
又因为 为等比数列, ,所以 ,
当 时, ;
当 时, ;
所以 ,
故选:D.
5、
【答 案】
D
【分析】
因为 , ,所以三角形 为正三角形,
所以 到直线 的距离为 ,所以 ,
因为 ,所以 ,所以 ,所以 .
因此正确答案为:D
6、
【答 案】
B
【分析】
通过题意得: ,当 时, ,
在 上单调递增, ,又 ,解得: ,
的最大值为 .
因此正确答案为: B.
7、
【答 案】
B
【分析】
观察 ,可考虑构造函数 ,求得 的奇偶性,再由 时, 的单调性
确定整个 增减性,由 与 的正负反推 正负即可求解.
设 ,则 ,∵当 时, ,
∴当 时, ,即 在 上单调递减.
由于 是奇函数,所以 , 是偶函数,
所以 在 上单调递增.
又 ,
当 或 时, ;
当 或 时, ,
所以当 或 时, .
即不等式 的解集为 .
故选:B.
8、
【答 案】
C
【分析】
利用基本不等式可求得 的最大值为 ,判断A、B;将 化为 ,结合基本不等
式可求得其最小值,判断C; ,结合 可判断D.
为正实数, ,
,而 共线,
,
当且仅当 时,结合 ,即 时取等号,A,B错误;
,
当且仅当 ,即 ,即 时取等号,
即 的最小值为4,C正确;
又 ,
由于 为正实数, ,则 ,
则 , 时 取最大值 ,
当 趋近于0时, 可无限趋近于0,
故 ,故 无最大值,D错误,
故选:C.
二、多选题
9、
【答 案】
A;B
【分析】
i i
对于A:因为 i,所以 i i i ,故A无误;
i i i
对于B:设 i ,代入 i ,得 ,整理得
,即点Z在直线 上,故B无误;
对于C: i是纯虚数,则 ,即 ,故C有误;
对于D:复数 i的虚部为 ,故D有误.
因此正确答案为:AB.
10、
【答案 】
A;D
【分析】
设切点为 ,则 ,所以切线方程为: ,切线过点A(a,
e e e e
0),代入得: ,即方程 有两个解,则有
e e
或 .
因此正确答 案为:AD.
11、
【答 案】
B;C;D
【分析】
对于A,由条件可得 垂直于 轴,然后可得四边形 的周长,对于B,由条件可得点 的横纵坐标,即
可得 的面积,对于C,设直线 ,然后联立抛物线的方程消元,然后得到 ,
然后结合基本不等式可得 的最小值,对于D,设直线 ,然后联立抛物线方程消元,然
后由 可求出 的值.
对于选项 ,由题意知 ,且 垂直于 轴,根据抛物线的定义可知 .
设 与 轴的交点为 ,易知 ,
故 ,
所以四边形 的周长为 ,选项 错误;
对于选项 ,由题意得 ,解得 ,所以 ,
从而 ,选项 正确;
对于选项 ,若直线 过点 ,设直线 ,
联立直线 与抛物线方程得 ,易得 ,
则 ,
所以 ,
当且仅当 时,等号成立,选项C正确;
对于选项D,设直线 ,联立直线 与抛物线方程得 ,
则 ,即 , ,所以 ,
由 可得 ,
即 ,解得 ,
故直线 的方程为 ,即直线 恒过定点 ,选项D正确.
故选:BCD.
12、
【答 案】
A;C;D
【分析】
A选项,利用三角形面积公式, ,当
时, 最大,且最大值为 ,故A正确;B选项,取 的中点 ,易证 ,易判断B错误;C选
项,三棱锥 体积最大时, 平面 , ,找到球心 求出半径
得解;D选项,由 ,得 ,所以点 在以 为球心,1为半径的球面上,求出点 到平面 的
距离得解.
对于A,由 , ,则 ,
所以当 时, 最大,且最大值为 ,故A正确;
对于B,取 的中点 ,连接 ,显然 ,且 ,
又 ,所以四边形 为平行四边形,
所以 ,又 ,且 , 为 的中点,
则 与 不垂直,
所以 与 不垂直 ,故B错;
对于C,易知三棱锥 体积最大时,平面 平面 ,交线为 ,
作 ,因为 平面 ,则 平面 ,
取 中点 ,连接 , , ,则 ,
由勾股定理可得 ,
又 ,故点 为三棱锥 的外接球的球心,
所以其外接球的半径为 ,表面积为 ,故C正确;
对于D,由选项C可知 , ,
点 在以 为球心,1为半径的球面上,设点 到平面 的距离为 ,
因为 ,所以 ,
易知 , , ,
, , ,
所以点 到平面 的距离的最小值为 ,选项D正确.
故选:ACD.
三、填空题
13、
【答案 】
【分析】
根据投影向量的求法求得正确答案.
由 ,得 ,又 ,
所以向量 在向量 上的投影向量的坐标为 .
故答案为:
14、
【答案 】
/
【分析】
利用二倍角公式、辅助角公式化简函数 ,再利用已知及和角的余弦公式求解即可.
依题意, ,
由 ,得 ,又 ,即 ,则
,
所以
.
故答案为:
15、
【答案 】
.
【分析】
由题意得 及 1,从而将问题转化为求 的取值范围,由此利用导数
研究其单调性即 可得解.
因为 与 在其定义域单调递增,
所以在各自定义域内不可能有两个点 使得 ,
又因为 ,所以由题意得 ,
故由 得 ,则 所以 ,
令 ,则 ,
所以 在 上单调递增,则 ,
故 ,即 .
故答案为: .
16、
【答 案】
【分析】
由已知条件求出 点轨迹方程,设点求点 到直线 的最小距离,或利用平行于直线
的切线求点 到直线 的最小距离.
如图可知: .
当 时,则交点为 ;当 时,则交点为 .
当 时,则 ,
于是可得 , ,
联立上式可得点 的轨迹方程为 .
又点 满足方程 ,故点 的轨迹方程为 .
法一:设 ,则 ,
当 时,距离最小,最小为 .
法二:点 的轨迹方程为: ,与 无公共点.
设直线 平行于直线 ,则直线 的方程可以写为 ,
由方程组 消去 ,得 .
令其根的判别式 ,得 .
由图知,当 时,直线 与 的公共点到直线 的距
离最小,
即两平行 直线 和 之间的距离,
所以最小距离为 .
故答案为:
四、解答题
17、
【答 案】
(1) .
(2)
【分析】
(1)由题意得 ,再利用等比数列和等差数列的性质列方程可求出 ,从而可求出公比
,进而可求得数列 与 的通项公式;
(2)由 ,得 ,两式相减可求得 ,再
验证 ,然后利用等比数列的求和公式可求得结果.
(1)设等比数列 的公比为 ,
由题意, ,
,解得 ,或 (舍去),
,
.
(2)由题意, ,①
,②
②-①得 ,
当 时, 不满足上式,所以 ,
.
18、
【答案 】
(1)
(2)
【分析】
(1)利用正弦定理化边为角,再结合两角和的正弦公式及三角形内角和定理化简即可得解;
(2)先利用正弦定理求出 ,再根据三角恒等变换化简,结合三角函数的性质即可得解.
(1)根据题意,由正弦定理得
,
又在锐角 中,有 ,所以 ,
所以 ,所以 ;
(2)结合(1)可得 ,
由 ,则根据正弦定理有 ,
得 ,
根据余弦定理有 ,得 ,
所以
,
又 为锐角三角形,则有 ,得 ,
所以 ,所以 ,
故 .
19、
【答 案】
(1)、
证明见解析
(2)、
【分析】
(1)、由题知 ,
,
又 , ,所以 ,
又 , , 平面 ,所以 平面 ,
又 平面 ,所以 ,
在正 中, 为 中点,于是 ,
又 , 平面 ,所以 平面 .
(2)、取 中点为 中点为 ,则 , ,
由(1)知, 平面 ,且 平面 ,所以 ,
又 ,所以 ,
又 , , 平面 ,
所以 平面 ,
于是 , , 两两垂直.
如图,以 为坐标原点, , , 的方向为 轴、 轴、 轴的正方向,建立空间直角坐标系,
则 , , , , , ,
所以 , , , .
设平面 的法向量为 ,
则 ,即 ,
令 ,则 ,
于是 .
设 ,
则 .
由于直线 与平面 所成角的正弦值为 ,
,
即 ,
整理得 ,
由于 ,所以
于是 .
设点 到平面 的距离为 ,
则 ,
所以点 到平面 的距离为 .
20、
【答 案】
(1)
(2)
【分析】
(1)根据乘法公式求概率即可;
(2)根据条件概率公式求概率即 可.
(1)由题意可知,第一轮队伍 和队伍 对阵,则获胜队伍需要赢得比赛3的胜利,失败队伍需要赢得比赛4和
比赛5的胜利,他们才能在决赛中对阵,
所以所求的概率为 .
(2)设 表示队伍 在比赛 中胜利, 表示队伍 在比赛 中失败,
设事件 :队伍 获得亚军,事件 队伍 所参加的所有比赛中败了两场,
则事件 包括 ,且这五种 情况彼此互斥,
进而
,
事件 包括 ,且这两种情况互斥,
进而 ,
所以所求事件 的概率为 .
21、
【答 案】
(1) (2)
【分析】
(1)根据题意求出 , , ,进而可求出结果;
(2)当矩形 的一组对边斜率不存在时,可 求出矩形 的面积;当矩形 四边斜率都存在时,
不防设 , 所在直线斜率为 ,则 , 斜率为 ,设出直线 的方程为 ,联立直线与椭
圆方程,结合韦达定理以及弦长公式等,即可求解.
解:(1)由题设条件可得 , ,解得 ,
∴ ,所以椭圆 的方程为
(2)当矩形 的一组对边斜率不存在时,得矩形 的面积
当矩形 四边斜率都存在时,不防设 , 所在直线斜率为 ,则 , 斜率为 ,
设直线 的方程为 ,与椭圆联立 可得
,
由 ,得
显然直线 的直线方程为 ,直线 , 间的距离
,
同理可求得 , 间的距离为
所以四边形 面积为
(等号当且仅当 时成立)
又 ,
故由以上可得外切矩形面积的 取值范围是
本题主要考查椭圆方程以及直线与椭圆的综合,灵活运用弦长公式,韦达定理等即可求解,属于常考题型.
22、
【答 案】
(1)答案见解析
(2)
【分析】
(1)由 得 ,
当 时, , 在区间 上单调递增,且 无限趋近于0时, ,
又 ,故 只有1个零点;
当 时,令 ,解得 ,令 ,解得 ,
故 在区间 上单调递减,在区间 上单调递增;
所以当 时, 取得最小值 ,
当 时, ,所以函数 无零点,
当 时, 恒成立,所以函数 无 零点,
综上所述,当 时, 无零点,当 时, 只有一个零点;
(2)由已知有 ,所以 ,
所以 ,
构造函数 ,则原不等式转 化为 在 上恒成立,
,记 ,所以 ,
令 ,解得 ,令 ,解得 ,
故 在区间 上单调递减,在区间 上单 调递增,
所以 ,所以 ,即 单调递增,
所以 在 上恒成立,
即 在 上恒成立,
令 , ,则 ,
令 ,解得 ,令 ,解得 ,
故 在 单调递减, 单调递增,
故 的最小值为 ,
\lne
故 的取值范围是 .
检测)
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 ( )
A.
B.
C.R
D.
2、使“ ”成立的一个充分不必要条件是( )
A.
B.
C.
D.
3、已知圆锥的侧面积(单位: )为 ,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:
)是( )
A.
B.
C.
D.
4、若 为等差数列, 是其前 项的和,且 为等比数列, ,则 的
值为( )
A.
B.
C.
D.
5、已知双曲线 的右焦点为 ,以 为圆心, 为半径的圆与双曲线的一条渐近线的
两个交点为 .若 ,则该双曲线的离心率为( )
A.
B.
C.
D.
6、将函数 在 上单调递增,则 的最大值为( )
A.
B.
C.
D.
7、设函数 是奇函数 的导函数, ,当 时, ,则不等式
的解集为( )
A.
B.
C.
D.
8、 中, 为 上一点且满足 ,若 为 上一点,且满足 为正实
数,则下列结论正确的是( )
A. 的最小值为
B. 的最大值为1
C. 的最小值为4
D. 的最大值为16
二、多选题(本大题共4小题,每小题5分,共20分)
9、已知i为虚数单位,下列说法正确的是( )
i
A.若复数 ,则
i
B.若复数z满足 i ,则复平面内z对应的点Z在一条直线上
C.若 i是纯虚数,则实数
D.复数 i的虚部为 i
10、已知过点A(a,0)作曲线 的切线有且仅有两条,则实数a的值可以是( )
A.-2
B.4
C.0
D.6
11、已知 是抛物线 的焦点, 是 上的两点, 为原点,则( )
A.若 垂直 的准线于点 ,且 ,则四边形 的周长为
B.若 ,则 的面积为
C.若直线 过点 ,则 的最小值为
D.若 ,则直线 恒过定点
12、如图,矩形 中, 为边 的中点,沿 将 折起,点 折至 处 平
面 分别在线段 和侧面 上运动,且 ,若 分别为线段 的中点,则在
折起过程中,下列说法正确的是( )
A. 面积的最大值为
B.存在某个位置,使得
C.三棱锥 体积最大时,三棱锥 的外接球的表面积为
D.三棱锥 体积最大时,点 到平面 的距离的最小值为 .
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知向量 ,则向量 在向量 上的投影向量的坐标为 .
14、已知函数 .若 ,则 .
15、已知函数 ,若 ,则实数 的取值范围为 .
16、如图,矩形 中, 分别为线段 上的动点,且满足
.点 关于原点的对称点为 ,直线 与 交于点 ,则点 到直线
的最小距离为 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知等比数列 的第二 三 四项分别是等差数列 的第二 五 十四项,且等差数列 的首项 ,公
差 .
(1)求数列 与 的通项公式;
(2)设数列 对任意 均有 成立,求 的值.
18、(本小题12分)
在锐角 中,内角 的对边分别为 ,已知 .
(1)求 ;
(2)若 ,求 的取值范围.
19、(本小题12分)
如图,在三棱柱 中, 为等边三角形,四边形 是边长为 的正方形, 为 中
点,且 .
(1)、求证: 平面 ;
(2)、若点 在线段 上,且直线 与平面 所成角的正弦值为 ,求点 到平面 的距离.
20、(本小题12分)
第19届杭州亚运会-电子竞技作为正式体育竞赛项目备受关注.已知某项赛事的季后赛后半段有四支战队参加,
采取“双败淘汰赛制”,对阵表如图,赛程如下:
第一轮:四支队伍分别两两对阵(即比赛1和2) ,两支获胜队伍进入胜者组,两支失败队伍落入败者组.
第二轮:胜者组两支队伍对阵(即比赛3),获胜队伍成为胜者组第一名,失败队伍落入败者组;第一轮 落入败
者组两支队伍对阵(即比赛4),失败队伍(已两败)被淘汰(获得殿军),获胜队伍留在败者组.
第三轮:败者组两支队伍对阵(即比赛5),失败队伍被淘汰(获得季军);获胜队伍成为败者组第 一名.
第四轮:败者组第一名和胜者组第一名决赛(即比赛6),争夺冠军.假设每场比赛双方获胜的概率均为0.5 ,每
场比赛之间相互独立.问:
(1)若第一轮队伍 和队伍 对阵,则他们仍能在决赛中对阵的概率是多少?
(2)已知队伍 在上述季后赛后半段所参加的所有比赛中,败了两场,求在该 条件下队伍 获得亚军的概率.
21、(本小题12分)
设椭圆 的离心率 ,椭圆上的点到左焦点 的距离的最大值为3.
(1)求椭圆 的方程;
(2)求椭圆 的外切矩形 的面积 的取值范围.
22、(本小题12分)
已知函数 .
(1)当 时,讨论函数 零点的 个数;
(2)当 时, 恒成立,求 的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
求出函数的定义域和值域,可分别化简集合 , ,再利用交集的定义求解即可.
依题意: , ,
所以 .
故选:A.
2、
【答 案】
D
【分析】
根据充分不必要条件的意思和不等式的性质可得答案.
只有当 同号时才有 ,故 错,
,故B错,
推不出 显然错 误,
,而反之不成立 ,故D满足题意,
故选:D.
3、
【答 案】
B
【分析】
利用扇形的面积公式 ,底面圆周长等于扇形弧长 ,即得解.
设圆锥底面半径为 ,母线长为 ,则
,解得 .
故选:B
4、
【答 案】
D
【分析】
根据等差数列以及等比数列的性质分别求得 的值,结合三角函数诱导公式化简求值,即得答案.
因为 为等差数列,故 ,
所以 ,
又因为 为等比数列, ,所以 ,
当 时, ;
当 时, ;
所以 ,
故选:D.
5、
【答 案】
D
【分析】
因为 , ,所以三角形 为正三角形,
所以 到直线 的距离为 ,所以 ,
因为 ,所以 ,所以 ,所以 .
因此正确答案为:D
6、
【答 案】
B
【分析】
通过题意得: ,当 时, ,
在 上单调递增, ,又 ,解得: ,
的最大值为 .
因此正确答案为: B.
7、
【答 案】
B
【分析】
观察 ,可考虑构造函数 ,求得 的奇偶性,再由 时, 的单调性
确定整个 增减性,由 与 的正负反推 正负即可求解.
设 ,则 ,∵当 时, ,
∴当 时, ,即 在 上单调递减.
由于 是奇函数,所以 , 是偶函数,
所以 在 上单调递增.
又 ,
当 或 时, ;
当 或 时, ,
所以当 或 时, .
即不等式 的解集为 .
故选:B.
8、
【答 案】
C
【分析】
利用基本不等式可求得 的最大值为 ,判断A、B;将 化为 ,结合基本不等
式可求得其最小值,判断C; ,结合 可判断D.
为正实数, ,
,而 共线,
,
当且仅当 时,结合 ,即 时取等号,A,B错误;
,
当且仅当 ,即 ,即 时取等号,
即 的最小值为4,C正确;
又 ,
由于 为正实数, ,则 ,
则 , 时 取最大值 ,
当 趋近于0时, 可无限趋近于0,
故 ,故 无最大值,D错误,
故选:C.
二、多选题
9、
【答 案】
A;B
【分析】
i i
对于A:因为 i,所以 i i i ,故A无误;
i i i
对于B:设 i ,代入 i ,得 ,整理得
,即点Z在直线 上,故B无误;
对于C: i是纯虚数,则 ,即 ,故C有误;
对于D:复数 i的虚部为 ,故D有误.
因此正确答案为:AB.
10、
【答案 】
A;D
【分析】
设切点为 ,则 ,所以切线方程为: ,切线过点A(a,
e e e e
0),代入得: ,即方程 有两个解,则有
e e
或 .
因此正确答 案为:AD.
11、
【答 案】
B;C;D
【分析】
对于A,由条件可得 垂直于 轴,然后可得四边形 的周长,对于B,由条件可得点 的横纵坐标,即
可得 的面积,对于C,设直线 ,然后联立抛物线的方程消元,然后得到 ,
然后结合基本不等式可得 的最小值,对于D,设直线 ,然后联立抛物线方程消元,然
后由 可求出 的值.
对于选项 ,由题意知 ,且 垂直于 轴,根据抛物线的定义可知 .
设 与 轴的交点为 ,易知 ,
故 ,
所以四边形 的周长为 ,选项 错误;
对于选项 ,由题意得 ,解得 ,所以 ,
从而 ,选项 正确;
对于选项 ,若直线 过点 ,设直线 ,
联立直线 与抛物线方程得 ,易得 ,
则 ,
所以 ,
当且仅当 时,等号成立,选项C正确;
对于选项D,设直线 ,联立直线 与抛物线方程得 ,
则 ,即 , ,所以 ,
由 可得 ,
即 ,解得 ,
故直线 的方程为 ,即直线 恒过定点 ,选项D正确.
故选:BCD.
12、
【答 案】
A;C;D
【分析】
A选项,利用三角形面积公式, ,当
时, 最大,且最大值为 ,故A正确;B选项,取 的中点 ,易证 ,易判断B错误;C选
项,三棱锥 体积最大时, 平面 , ,找到球心 求出半径
得解;D选项,由 ,得 ,所以点 在以 为球心,1为半径的球面上,求出点 到平面 的
距离得解.
对于A,由 , ,则 ,
所以当 时, 最大,且最大值为 ,故A正确;
对于B,取 的中点 ,连接 ,显然 ,且 ,
又 ,所以四边形 为平行四边形,
所以 ,又 ,且 , 为 的中点,
则 与 不垂直,
所以 与 不垂直 ,故B错;
对于C,易知三棱锥 体积最大时,平面 平面 ,交线为 ,
作 ,因为 平面 ,则 平面 ,
取 中点 ,连接 , , ,则 ,
由勾股定理可得 ,
又 ,故点 为三棱锥 的外接球的球心,
所以其外接球的半径为 ,表面积为 ,故C正确;
对于D,由选项C可知 , ,
点 在以 为球心,1为半径的球面上,设点 到平面 的距离为 ,
因为 ,所以 ,
易知 , , ,
, , ,
所以点 到平面 的距离的最小值为 ,选项D正确.
故选:ACD.
三、填空题
13、
【答案 】
【分析】
根据投影向量的求法求得正确答案.
由 ,得 ,又 ,
所以向量 在向量 上的投影向量的坐标为 .
故答案为:
14、
【答案 】
/
【分析】
利用二倍角公式、辅助角公式化简函数 ,再利用已知及和角的余弦公式求解即可.
依题意, ,
由 ,得 ,又 ,即 ,则
,
所以
.
故答案为:
15、
【答案 】
.
【分析】
由题意得 及 1,从而将问题转化为求 的取值范围,由此利用导数
研究其单调性即 可得解.
因为 与 在其定义域单调递增,
所以在各自定义域内不可能有两个点 使得 ,
又因为 ,所以由题意得 ,
故由 得 ,则 所以 ,
令 ,则 ,
所以 在 上单调递增,则 ,
故 ,即 .
故答案为: .
16、
【答 案】
【分析】
由已知条件求出 点轨迹方程,设点求点 到直线 的最小距离,或利用平行于直线
的切线求点 到直线 的最小距离.
如图可知: .
当 时,则交点为 ;当 时,则交点为 .
当 时,则 ,
于是可得 , ,
联立上式可得点 的轨迹方程为 .
又点 满足方程 ,故点 的轨迹方程为 .
法一:设 ,则 ,
当 时,距离最小,最小为 .
法二:点 的轨迹方程为: ,与 无公共点.
设直线 平行于直线 ,则直线 的方程可以写为 ,
由方程组 消去 ,得 .
令其根的判别式 ,得 .
由图知,当 时,直线 与 的公共点到直线 的距
离最小,
即两平行 直线 和 之间的距离,
所以最小距离为 .
故答案为:
四、解答题
17、
【答 案】
(1) .
(2)
【分析】
(1)由题意得 ,再利用等比数列和等差数列的性质列方程可求出 ,从而可求出公比
,进而可求得数列 与 的通项公式;
(2)由 ,得 ,两式相减可求得 ,再
验证 ,然后利用等比数列的求和公式可求得结果.
(1)设等比数列 的公比为 ,
由题意, ,
,解得 ,或 (舍去),
,
.
(2)由题意, ,①
,②
②-①得 ,
当 时, 不满足上式,所以 ,
.
18、
【答案 】
(1)
(2)
【分析】
(1)利用正弦定理化边为角,再结合两角和的正弦公式及三角形内角和定理化简即可得解;
(2)先利用正弦定理求出 ,再根据三角恒等变换化简,结合三角函数的性质即可得解.
(1)根据题意,由正弦定理得
,
又在锐角 中,有 ,所以 ,
所以 ,所以 ;
(2)结合(1)可得 ,
由 ,则根据正弦定理有 ,
得 ,
根据余弦定理有 ,得 ,
所以
,
又 为锐角三角形,则有 ,得 ,
所以 ,所以 ,
故 .
19、
【答 案】
(1)、
证明见解析
(2)、
【分析】
(1)、由题知 ,
,
又 , ,所以 ,
又 , , 平面 ,所以 平面 ,
又 平面 ,所以 ,
在正 中, 为 中点,于是 ,
又 , 平面 ,所以 平面 .
(2)、取 中点为 中点为 ,则 , ,
由(1)知, 平面 ,且 平面 ,所以 ,
又 ,所以 ,
又 , , 平面 ,
所以 平面 ,
于是 , , 两两垂直.
如图,以 为坐标原点, , , 的方向为 轴、 轴、 轴的正方向,建立空间直角坐标系,
则 , , , , , ,
所以 , , , .
设平面 的法向量为 ,
则 ,即 ,
令 ,则 ,
于是 .
设 ,
则 .
由于直线 与平面 所成角的正弦值为 ,
,
即 ,
整理得 ,
由于 ,所以
于是 .
设点 到平面 的距离为 ,
则 ,
所以点 到平面 的距离为 .
20、
【答 案】
(1)
(2)
【分析】
(1)根据乘法公式求概率即可;
(2)根据条件概率公式求概率即 可.
(1)由题意可知,第一轮队伍 和队伍 对阵,则获胜队伍需要赢得比赛3的胜利,失败队伍需要赢得比赛4和
比赛5的胜利,他们才能在决赛中对阵,
所以所求的概率为 .
(2)设 表示队伍 在比赛 中胜利, 表示队伍 在比赛 中失败,
设事件 :队伍 获得亚军,事件 队伍 所参加的所有比赛中败了两场,
则事件 包括 ,且这五种 情况彼此互斥,
进而
,
事件 包括 ,且这两种情况互斥,
进而 ,
所以所求事件 的概率为 .
21、
【答 案】
(1) (2)
【分析】
(1)根据题意求出 , , ,进而可求出结果;
(2)当矩形 的一组对边斜率不存在时,可 求出矩形 的面积;当矩形 四边斜率都存在时,
不防设 , 所在直线斜率为 ,则 , 斜率为 ,设出直线 的方程为 ,联立直线与椭
圆方程,结合韦达定理以及弦长公式等,即可求解.
解:(1)由题设条件可得 , ,解得 ,
∴ ,所以椭圆 的方程为
(2)当矩形 的一组对边斜率不存在时,得矩形 的面积
当矩形 四边斜率都存在时,不防设 , 所在直线斜率为 ,则 , 斜率为 ,
设直线 的方程为 ,与椭圆联立 可得
,
由 ,得
显然直线 的直线方程为 ,直线 , 间的距离
,
同理可求得 , 间的距离为
所以四边形 面积为
(等号当且仅当 时成立)
又 ,
故由以上可得外切矩形面积的 取值范围是
本题主要考查椭圆方程以及直线与椭圆的综合,灵活运用弦长公式,韦达定理等即可求解,属于常考题型.
22、
【答 案】
(1)答案见解析
(2)
【分析】
(1)由 得 ,
当 时, , 在区间 上单调递增,且 无限趋近于0时, ,
又 ,故 只有1个零点;
当 时,令 ,解得 ,令 ,解得 ,
故 在区间 上单调递减,在区间 上单调递增;
所以当 时, 取得最小值 ,
当 时, ,所以函数 无零点,
当 时, 恒成立,所以函数 无 零点,
综上所述,当 时, 无零点,当 时, 只有一个零点;
(2)由已知有 ,所以 ,
所以 ,
构造函数 ,则原不等式转 化为 在 上恒成立,
,记 ,所以 ,
令 ,解得 ,令 ,解得 ,
故 在区间 上单调递减,在区间 上单 调递增,
所以 ,所以 ,即 单调递增,
所以 在 上恒成立,
即 在 上恒成立,
令 , ,则 ,
令 ,解得 ,令 ,解得 ,
故 在 单调递减, 单调递增,
故 的最小值为 ,
\lne
故 的取值范围是 .
同课章节目录
