用一元二次方程解决问题 专项练习(含解析)
文档属性
| 名称 | 用一元二次方程解决问题 专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 789.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 04:54:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
用一元二次方程解决问题 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级下·安徽合肥·期中)某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支.已知1个主干长出的枝干和小分支的总数是56,则这种植物每个枝干长出小分支的个数是( )
A.9 B.8 C.7 D.6
2.(23-24九年级上·海南省直辖县级单位·期末)一个两位数等于它的个位数的平方,且个位数字比十位数字大,则这个两位数为( )
A.25 B.36 C.25或36 D.或
3.(2024·四川眉山·中考真题)眉山市东坡区永丰村是“天府粮仓”示范区,该村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩产量从2021年的670千克增长到了2023年的780千克,该村水稻亩产量年平均增长率为,则可列方程为( )
A. B.
C. D.
4.(23-24八年级下·吉林长春·期中)某小区计划在一块长32m、宽20m的长方形空地上修建三条同样宽的道路(如图),剩余的空地上种植草坪,使草坪的面积为.设道路的宽为xm,则下面所列方程正确的是( )
A. B.
C. D.
5.(23-24九年级下·山东淄博·期中)某连锁超市购进一款年货大礼包,经调研发现,当该款大礼包每盒的售价为元时,每天可售出盒,每盒的售价每降低元,每天的销量增加盒,要使该款大礼包每天的销售额达到元,每盒的售价应降低多少元?若设该款大礼包每盒降价元,则可列方程为( )
A. B.
C. D.
6.(23-24九年级上·山东德州·阶段练习)如图,中,,, 动点P从点A出发沿边以/秒的速度向点 B移动,点 Q从点B出发,沿边以/秒的速度向点C移动,如果点P,Q分别从点A,B同时出发,在运动过程中,设点P的运动时间为 t,则当的面积为时,t的值 ( )
A.2 或3 B.2或4 C.1或3 D.1或4
7.(23-24八年级下·浙江温州·期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C. D.
8.(23-24九年级上·河北廊坊·期末)某电商销售一款进价为80元/台的电吹风,若按每台120元出售,当月可销售50台,经调查发现这款电吹风的售价每下降3元,其销售数量增加10台.设售价为x元/台.若使该电商销售这款电吹风的利润为2500元,则可列方程为( )
A. B.
C. D.
9.(22-23九年级上·江苏无锡·期末)某超市销售一种可拆分式驱蚊器,一套驱蚊器由一个加热器和一瓶电热蚊香液组成,电热蚊香液作为易耗品可单独购买.一套驱蚊器的售价是一瓶电热蚊香液的5倍,已知一瓶电热蚊香液的利润率为20%,一套驱蚊器的利润率为25%.超市出售1套驱蚊器和4瓶电热蚊香液,共可获利10元.经过一段时间的销售发现,每天能销售50套驱蚊器和80瓶电热蚊香液,为了促进驱蚊器的销售,超市决定对驱蚊器降价处理,其中每降价1元,可多卖出5套.若超市每天销售驱蚊器要获得275元的利润,则每套需降价( )
A.1元 B.2元 C.3元 D.4元
10.(2024九年级·全国·竞赛)由于技术水平的不断提高,某些石材加工设备的生产成本不断降低,下表是甲、乙两种设备分别在2012年和2014年每套的生产成本情况.
年份 甲种设备的生产成本(元/台) 乙种设备的生产成本(元/台)
2012年 50000 60000
2014年 28125 33750
现有下列结论:
①从2012年到2014年,甲种设备的生产成本年平均下降率为;
②从2012年到2014年,乙种设备的生产成本的年平均下降率比甲种设备大;
③按甲种设备生产成本的年平均下降率估计,2013年甲种设备平均每台的生产成本为元;
④若乙种设备生产成本的年平均下降率不变,则估计2016年,乙种设备每台的生产成本为元.其中正确的结论有( )
A.①④ B.①②④ C.①③ D.②③④
二、填空题(本大题共8小题,每小题4分,共32分)
11.(22-23九年级上·山西忻州·阶段练习)某中学九年级(4)班在毕业典礼上,每两位同学都相互握了一次手,有人统计一共握了465次手,则九年级(4)班的同学共有 名.(参考数据:)
12.(2024·河南商丘·三模)4月初,“胖东来启动帮扶步步高超市”这一词条冲上热搜,得到帮扶后的步步高超市4 月11日当天的营业额是21万元,4月 13 日的营业额是80万元,假设营业额每天的平均增长率相同,可设为x,那么可列出的方程是 .
13.(2024九年级·全国·竞赛)有一面墙长米,高米,中间有一个背景墙(阴影部分与黑色部分),如图所示,已知背景墙的边框(黑色部分)长度为米,高米,面积为整面墙的面积的,那么背景墙边框的宽度为 米.
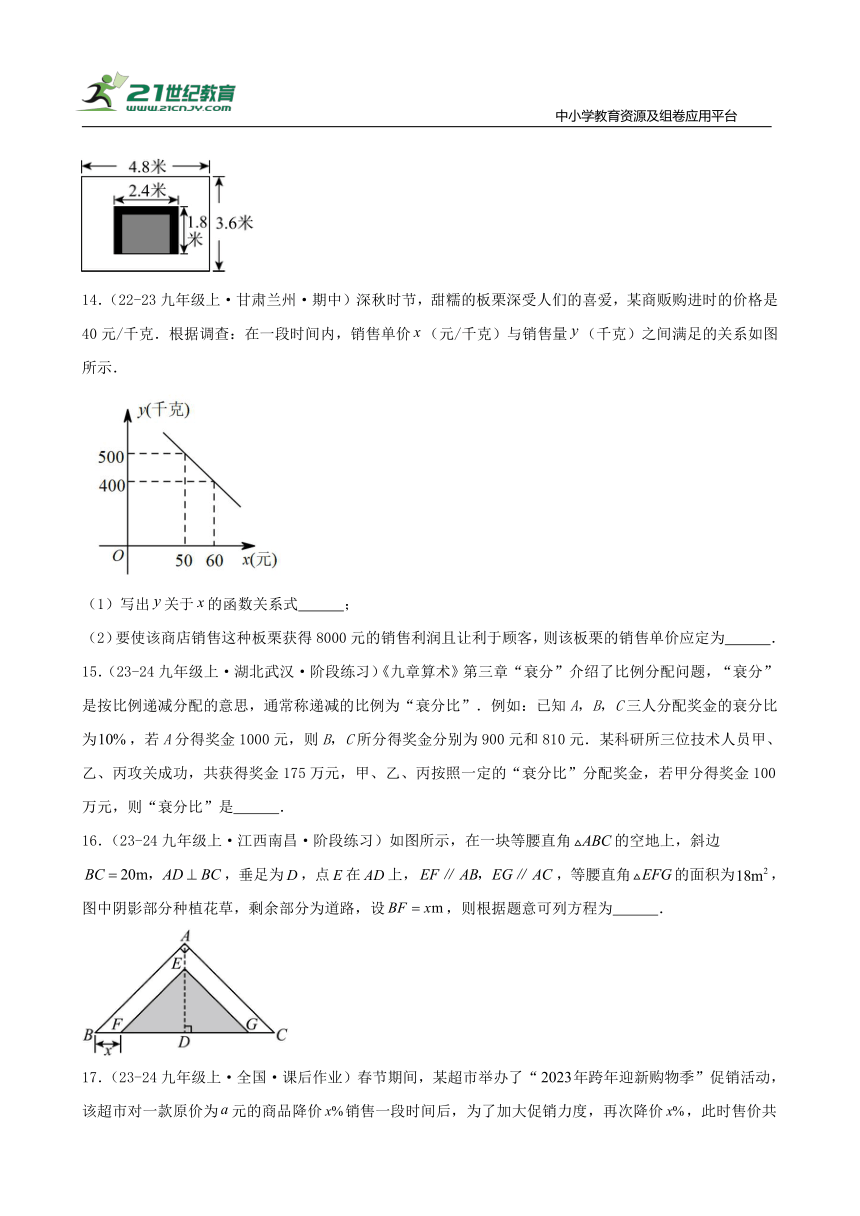
14.(22-23九年级上·甘肃兰州·期中)深秋时节,甜糯的板栗深受人们的喜爱,某商贩购进时的价格是40元/千克.根据调查:在一段时间内,销售单价(元/千克)与销售量(千克)之间满足的关系如图所示.
(1)写出关于的函数关系式 ;
(2)要使该商店销售这种板栗获得8000元的销售利润且让利于顾客,则该板栗的销售单价应定为 .
15.(23-24九年级上·湖北武汉·阶段练习)《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.例如:已知A,B,C三人分配奖金的衰分比为,若A分得奖金1000元,则B,C所分得奖金分别为900元和810元.某科研所三位技术人员甲、乙、丙攻关成功,共获得奖金175万元,甲、乙、丙按照一定的“衰分比”分配奖金,若甲分得奖金100万元,则“衰分比”是 .
16.(23-24九年级上·江西南昌·阶段练习)如图所示,在一块等腰直角的空地上,斜边,垂足为,点在上,,等腰直角的面积为,图中阴影部分种植花草,剩余部分为道路,设,则根据题意可列方程为 .
17.(23-24九年级上·全国·课后作业)春节期间,某超市举办了“年跨年迎新购物季”促销活动,该超市对一款原价为元的商品降价销售一段时间后,为了加大促销力度,再次降价,此时售价共降低了元,则 .
18.(2024七年级·全国·竞赛)如图,已知正方形的边长为10厘米,点在边上,且厘米,、两点分别从、两点出发以1厘米/秒的速度沿正方形的边逆时针移动,当点移到点时,、两点同时停止移动,设移动时间为秒,当时, .
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24九年级上·湖北襄阳·阶段练习)某名同学参加了学校统一组织的某项实验培训,回到班上后,第一节课他教会了若干名同学,第二节课会做的同学每人又教会了同样多的同学,这样全班共有36名同学会做这项实验.求每节课每名同学教会多少名同学做实验?
20.(8分)(23-24八年级下·福建福州·阶段练习)公安部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定. 某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售1500个,6月份销售2160个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)按照这个增长率,预计7月份该品牌头盔销售量是多少?
21.(10分)(22-23八年级下·浙江杭州·期中)如图1,有长为24米的篱笆,一面利用墙(墙的最大可用长度为15米),围成中间隔有一道篱笆的长方形花圃.
(1)如果要围成面积为36平方米的花圃,的长是多少米?
(2)如图2,如果在平行于墙面的篱笆上开两道1米宽的门,如果要围成面积为55平方米的花圃,的长时多少?
22.(10分)(23-24八年级下·浙江宁波·期中)每年的4月12日为载人空间飞行国际日,也是世界航天日.我国在2023年完成“天宫空间站”的在轨建造,取得了举世瞩目的航天成就.某商店为满足航天爱好者的需求,特推出“天宫空间站”系列A、B两款模型,A款模型比B款模型售价低20元,800元购买A款模型的数量与960元购买B款模型的数量相等.按定价销售一段时间后发现B款模型每天可以卖15件.为扩大销售,该商店准备适当降价,经过一段时间测算,B款模型每降价5元,则每天可以多卖1件.
(1)A、B两款模型每件售价分别是多少?
(2)为了使B款模型每天的销售额为1900元,而且尽可能让顾客得到实惠,求B款模型的降价后的售价为多少元/件?
23.(10分)(23-24八年级下·浙江杭州·期中)东新社区为了解决社区停车难的问题,利用一块矩形空地建了一个小型体车场,其布局如图所示,已知,,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x米的道路.已知铺花砖的面积(即阴影面积)为.
(1)求道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10120元,同时尽可能让利于居民?
24.(12分)(2024·山东德州·一模)为了节约用水,不少城市对用水大户作出了两段收费的规定,某市规定:月用水量不超过规定标准吨时,按每吨1.6元的价格交费,如果超过了标准,超标部分每吨还要加收元的附加费用.据统计,某户7、8两月的用水量和交费情况如下表:
月份 用水量(吨) 交费总数(元)
7 140 264
8 95 152
(1)求出该市规定标准用水量的值;
(2)当用水量超过标准吨时,写出交费总数(元)与用水量(吨)的函数关系式,并利用函数关系计算,当某月份用水量为150吨时,应交水费多少元?
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查一元二次方程的实际应用,理解题意找出等量关系是解题关键.设这种植物每个支干长出的小分支个数是x,根据题意可列出关于x的方程,再求解即可.
【详解】解:设这种植物每个支干长出的小分支个数是x,
依题意得:,
解得:(不合题意,舍去),,
∴这种植物每个支干长出的小分支个数是8.
故选:C.
2.C
【分析】本题考查了一元二次方程的应用,设十位上的数字为,则个位上的数字为,根据“一个两位数等于它的个位数的平方”列出一元二次方程,解方程即可得出答案,理解题意,找准等量关系,正确列出方程是解此题的关键.
【详解】解:设十位上的数字为,则个位上的数字为,
由题意得:,
整理得:,
解得:或,
当时,,此时这个两位数为,
当时,,此时这个两位数为,
综上所述,这个两位数为25或36,
故选:C.
3.B
【分析】本题主要考查一元二次方程的应用,熟练掌握一元二次方程的应用是解题的关键.
设该村水稻亩产量年平均增长率为,根据题意列出方程即可.
【详解】解:根据题意得:.
故选:B.
4.C
【分析】本题考查列一元二次方程解实际应用题.将三条路平移,草坪是一个长方形,如图所示,根据剩余的空地上种植草坪,使草坪的面积为,设道路的宽为,利用长方形面积公式得到,从而确定答案.
【详解】解:将三条路平移,如图所示:
剩余的空地上种植草坪,使草坪的面积为,设道路的宽度,
,
故选:C.
5.D
【分析】本题主要考查了由实际问题抽象出一元二次方程,设该款大礼包每盒降价元,根据题意列出一元二次方程,即可求解.
【详解】若设该款大礼包每盒降价元,则可列方程为
故选:D.
6.B
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.当运动时间为t秒时,,根据的面积为,即可得出关于t的一元二次方程,解之即可得出t的值.
【详解】解:当运动时间为t秒时,,
依题意得:
,
整理得:,
解得:.
故选:B.
7.C
【分析】本题考查一元二次方程的实际应用,利用互赠的数量加上老师赠送的数量等于总数量,列出方程即可.
【详解】解:设班级有x名学生,由题意,得:;
故选C.
8.D
【分析】本题考查了一元二次方程的应用,设售价为x元/台,根据利润销售量每台风扇的利润,列方程即可.
【详解】解:设售价为x元/台,
根据题意可得:,
故选:D.
9.A
【分析】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.设一瓶电热蚊香液的进价为x元,则电热蚊香液的售价为元,则一套驱蚊器的售价为6x元,进价为元,列出方程解出即可;
【详解】解:设一瓶电热蚊香液的进价为x元,则电热蚊香液的售价为元,则一套驱蚊器的售价为6x元,进价为元,由题意得:
,
解得:x=5,
所以一套驱蚊器的售价为:5×6=30(元),一套驱蚊器的利润元
设每套驱蚊器降价a元,由题意得:
,
解得: , (舍去),
故选:A.
10.A
【分析】本题主要考查一元二次方程的应用---增长率问题,根据增长率模型可逐项分析各选项进行判断即可得出结论.
【详解】解:①设甲种设备的生产成本年平均下降率为x,根据题意得:
解得,(舍去)
所以,甲种设备的生产成本年平均下降率为,①正确;
②设乙种设备的生产成本年平均下降率为y,根据题意得:
解得,(舍去)
所以,乙种设备的生产成本年平均下降率为,
即甲、乙两种设备的生产成本年平均下降率相同,②错误;
③2013年甲种设备平均每台的生产成本为,③错误;
④若乙种设备生产成本的年平均下降率不变,则估计2016年,乙种设备每台的生产成本为元,④是正确的.
综上,正确的结论是①④,
故选:A.
11.31
【分析】设九年级(4)班的同学共有x名,根据题意可得,解方程求解即可.
【详解】设九年级(4)班的同学共有x名,
依题意得:,
整理得:,
解得:(不符合题意,舍去),
∴九年级(4)班的同学共有31名.
故答案为:31.
【点睛】本题考查了一元二次方程的应用—传播问题,准确理解题意,熟练掌握知识点是解题的关键.
12.
【分析】本题考查了一元二次方程的应用中的增长率问题,找到关键描述语,就能找到等量关系,是解决问题的关键.主要考查增长率问题,一般用增长后的量=增长前的量增长率,用x表示4月 13 日的营业额即可得解.
【详解】解:依题意得4月 13 日的营业额,
∴.
故答案为:.
13./
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
设背景墙边框的宽度为,可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【详解】解:设背景墙边框的宽度为,得
解得(舍)
故答案为:.
14. 60
【分析】(1)设关于的函数关系式为,用待定系数法列方程组求解即可;
(2)根据利润=(售价-进价)×销量,列出方程求解即可得到答案.
【详解】解:(1)设关于的函数关系式为,
由图可知,点,在,
,
解得,
关于的函数关系式为,
故答案为;
(2)根据题意可得:
,
解得:或,
让利于顾客,
,
板栗的销售单价应定为60元,
故答案为:60.
【点睛】本题考查了一次函数和一元二次方程的应用,解题的关键是读懂题意,列出函数关系式和方程解决问题.
15.
【分析】本题考查了一元二次方程的实际应用,设“衰分比”为x,则乙获得奖金,丙获得奖金,根据甲、乙、丙共获得奖金175万元,列出方程求解,根据实际选择适合的值即可.
【详解】解:设“衰分比”为x,则乙获得奖金,丙获得奖金,
根据题意得:,
解得:或(舍去,不符合实际),
“衰分比”是,
故答案为:.
16.
【分析】本题考查了与图形有关的一元二次方程的应用,等腰三角形的性质,直角三角形的性质,读懂题意列出方程是关键.由等腰三角形的性质及平行条件,得点D是的中点,则,从而可表示出、,由面积关系建立方程即可.
【详解】解:∵是等腰直角三角形,,
∴,;
∵,
∴,
∴,
∴;
∵,点在上,
∴,
∴;
∵,
∴,
∴,
∴;
∵
∴.
故答案为:.
17.
【分析】根据某超市对一款原价位元的商品降价销售一段时间后,为了加大促销力度,再次降价,此时售价降低了元,列方程即可得到结论.
【详解】解:由题意得:,
故答案为:.
【点睛】此题考查了由实际问题抽象出一元二次方程,正确理解题意是解题的关键.
18.或18
【分析】本题考查一元二次方程在几何中的应用,根据移动时间为秒,分以下两种情况讨论,①当在上时,②当在上时,根据这两种情况分别用表示出和的底和高,根据建立方程求解,即可解题.
【详解】解:移动时间为秒,正方形的边长为10厘米,厘米,
①当在上时,
有厘米,厘米,厘米,
,
,即,
整理得,解得(不合题意,舍去),.
②当在上时,
则厘米,厘米,
,
整理得,解得,(不符合题意,舍去),
综上所述,的值为或18.
故答案为:或18.
19.5
【分析】此题主要考查了一元二次方程的应用,根据题意表示出两节课教会的人数是解题关键.
设平均每节课一人教会x人,第一节课后会做的有人,第二节课教会人,会做的有人,据此列方程求解即可.
【详解】解:设每节课一人教会x人,根据题意可得:
,
解得:(不合题意舍去)
答:每节课一人教会5人.
20.(1)
(2)2592
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设该品牌头盔销售量的月增长率为x,根据题意列出一元二次方程求解即可;
(2)根据题意列式计算即可.
【详解】(1)解:设该品牌头盔销售量的月增长率为x,
依题意,得:,
解得:,(不合题意,舍去).
∴该品牌头盔销售量的月增长率为;
(2)(个).
∴预计7月份该品牌头盔销售量是2592个.
21.(1)的长是米
(2)的长是米或米
【分析】本题主要考查了一元二次方程的实际应用,利用长方形的面积运算方法列出方程是解题的关键.
(1)设的长为米,则的长为米,根据长方形的面积=长宽列出方程运算即可;
(2)设的长为米,则的长为米,根据长方形的面积=长宽列出方程运算即可.
【详解】(1)解:设的长为米,则的长为米,
根据题意得:,
解得,,
当时,,不符合题意,
当时,,符合题意,
∴的长是6米;
(2)设的长为米,则的长为米,
根据题意得:,
解得,,
当时,,符合题意,
当m=6时,,符合题意,
∴的长是米或米.
22.(1)A模型每件售价100元,B模型每件售价120元
(2)95元
【分析】本题主要考查了分式方程的应用,一元二次方程的应用,
(1)根据800元购买A款模型的数量等于960元购买B款模型的数量列出分式方程,求出解即可;
(2)根据销售量乘以单价等于销售额列出一元二次方程,根据让顾客得到实惠求出解即可.
【详解】(1)解:设A模型每件售价x元,根据题意,得
∴
解得,
经检验:是方程的解,
∴,
答:A模型每件售价100元,B模型每件售价120元;
(2)解:设B模型每件下降元,根据题意,得
∴,
解得,,
∵尽可能实惠,
∴,
∴,
答:实际售价应为95元.
23.(1)米
(2)上涨元
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)道路的宽为米,根据铺花砖的面积 (即阴影面积)为 ,结合其布局图,列出一元二次方程,解方程取符合题意的值即可;
(2)设每个车位的月租金上涨元时,停车场的月租金收入为元,根据“该停车场共有车位个,据调查分析,当每个车位的月租金为元时,可全部租出;若每个车位的月租金每上涨元,就会少租出个车位”,列出一元二次方程,解方程取尽可能让利于居民的值即可.
【详解】(1)道路的宽为米,
由题意得:
整理得:
解得: (不合题意,舍去),
答:道路的宽是米;
(2)设每个车位的月租金上涨元时,停车场的月租金收入元,
由题意得:,
整理得:,
解得:,
∵尽可能让利于居民,
,
答:每个车位的月租金上涨元时,停车场的月租金收入为元.
24.(1)
(2),290元
【分析】本题考查了一元二次方程的应用、一次函数的应用,理解题意,正确得出一元二次方程以及一次函数是解此题的关键.
(1)根据七月份用水量以及交费总数得出关于的方程,解方程即可得出答案;
(2)当,根据收费方式即可得出交费总数(元)与用水量(吨)的函数关系式,求出当的值即可得解.
【详解】(1)解:因七月份用水量为140吨,,
所以需加收:(元),
即,
解得,,
又8月份用水量为95吨,,不超标,
故答案为;
(2)解:当时,则.
∴,
用水量为150吨时,应交水费:(元).
答:当某月份用水量为150吨时,应交水费290元.
用一元二次方程解决问题 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级下·安徽合肥·期中)某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支.已知1个主干长出的枝干和小分支的总数是56,则这种植物每个枝干长出小分支的个数是( )
A.9 B.8 C.7 D.6
2.(23-24九年级上·海南省直辖县级单位·期末)一个两位数等于它的个位数的平方,且个位数字比十位数字大,则这个两位数为( )
A.25 B.36 C.25或36 D.或
3.(2024·四川眉山·中考真题)眉山市东坡区永丰村是“天府粮仓”示范区,该村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩产量从2021年的670千克增长到了2023年的780千克,该村水稻亩产量年平均增长率为,则可列方程为( )
A. B.
C. D.
4.(23-24八年级下·吉林长春·期中)某小区计划在一块长32m、宽20m的长方形空地上修建三条同样宽的道路(如图),剩余的空地上种植草坪,使草坪的面积为.设道路的宽为xm,则下面所列方程正确的是( )
A. B.
C. D.
5.(23-24九年级下·山东淄博·期中)某连锁超市购进一款年货大礼包,经调研发现,当该款大礼包每盒的售价为元时,每天可售出盒,每盒的售价每降低元,每天的销量增加盒,要使该款大礼包每天的销售额达到元,每盒的售价应降低多少元?若设该款大礼包每盒降价元,则可列方程为( )
A. B.
C. D.
6.(23-24九年级上·山东德州·阶段练习)如图,中,,, 动点P从点A出发沿边以/秒的速度向点 B移动,点 Q从点B出发,沿边以/秒的速度向点C移动,如果点P,Q分别从点A,B同时出发,在运动过程中,设点P的运动时间为 t,则当的面积为时,t的值 ( )
A.2 或3 B.2或4 C.1或3 D.1或4
7.(23-24八年级下·浙江温州·期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C. D.
8.(23-24九年级上·河北廊坊·期末)某电商销售一款进价为80元/台的电吹风,若按每台120元出售,当月可销售50台,经调查发现这款电吹风的售价每下降3元,其销售数量增加10台.设售价为x元/台.若使该电商销售这款电吹风的利润为2500元,则可列方程为( )
A. B.
C. D.
9.(22-23九年级上·江苏无锡·期末)某超市销售一种可拆分式驱蚊器,一套驱蚊器由一个加热器和一瓶电热蚊香液组成,电热蚊香液作为易耗品可单独购买.一套驱蚊器的售价是一瓶电热蚊香液的5倍,已知一瓶电热蚊香液的利润率为20%,一套驱蚊器的利润率为25%.超市出售1套驱蚊器和4瓶电热蚊香液,共可获利10元.经过一段时间的销售发现,每天能销售50套驱蚊器和80瓶电热蚊香液,为了促进驱蚊器的销售,超市决定对驱蚊器降价处理,其中每降价1元,可多卖出5套.若超市每天销售驱蚊器要获得275元的利润,则每套需降价( )
A.1元 B.2元 C.3元 D.4元
10.(2024九年级·全国·竞赛)由于技术水平的不断提高,某些石材加工设备的生产成本不断降低,下表是甲、乙两种设备分别在2012年和2014年每套的生产成本情况.
年份 甲种设备的生产成本(元/台) 乙种设备的生产成本(元/台)
2012年 50000 60000
2014年 28125 33750
现有下列结论:
①从2012年到2014年,甲种设备的生产成本年平均下降率为;
②从2012年到2014年,乙种设备的生产成本的年平均下降率比甲种设备大;
③按甲种设备生产成本的年平均下降率估计,2013年甲种设备平均每台的生产成本为元;
④若乙种设备生产成本的年平均下降率不变,则估计2016年,乙种设备每台的生产成本为元.其中正确的结论有( )
A.①④ B.①②④ C.①③ D.②③④
二、填空题(本大题共8小题,每小题4分,共32分)
11.(22-23九年级上·山西忻州·阶段练习)某中学九年级(4)班在毕业典礼上,每两位同学都相互握了一次手,有人统计一共握了465次手,则九年级(4)班的同学共有 名.(参考数据:)
12.(2024·河南商丘·三模)4月初,“胖东来启动帮扶步步高超市”这一词条冲上热搜,得到帮扶后的步步高超市4 月11日当天的营业额是21万元,4月 13 日的营业额是80万元,假设营业额每天的平均增长率相同,可设为x,那么可列出的方程是 .
13.(2024九年级·全国·竞赛)有一面墙长米,高米,中间有一个背景墙(阴影部分与黑色部分),如图所示,已知背景墙的边框(黑色部分)长度为米,高米,面积为整面墙的面积的,那么背景墙边框的宽度为 米.
14.(22-23九年级上·甘肃兰州·期中)深秋时节,甜糯的板栗深受人们的喜爱,某商贩购进时的价格是40元/千克.根据调查:在一段时间内,销售单价(元/千克)与销售量(千克)之间满足的关系如图所示.
(1)写出关于的函数关系式 ;
(2)要使该商店销售这种板栗获得8000元的销售利润且让利于顾客,则该板栗的销售单价应定为 .
15.(23-24九年级上·湖北武汉·阶段练习)《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.例如:已知A,B,C三人分配奖金的衰分比为,若A分得奖金1000元,则B,C所分得奖金分别为900元和810元.某科研所三位技术人员甲、乙、丙攻关成功,共获得奖金175万元,甲、乙、丙按照一定的“衰分比”分配奖金,若甲分得奖金100万元,则“衰分比”是 .
16.(23-24九年级上·江西南昌·阶段练习)如图所示,在一块等腰直角的空地上,斜边,垂足为,点在上,,等腰直角的面积为,图中阴影部分种植花草,剩余部分为道路,设,则根据题意可列方程为 .
17.(23-24九年级上·全国·课后作业)春节期间,某超市举办了“年跨年迎新购物季”促销活动,该超市对一款原价为元的商品降价销售一段时间后,为了加大促销力度,再次降价,此时售价共降低了元,则 .
18.(2024七年级·全国·竞赛)如图,已知正方形的边长为10厘米,点在边上,且厘米,、两点分别从、两点出发以1厘米/秒的速度沿正方形的边逆时针移动,当点移到点时,、两点同时停止移动,设移动时间为秒,当时, .
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24九年级上·湖北襄阳·阶段练习)某名同学参加了学校统一组织的某项实验培训,回到班上后,第一节课他教会了若干名同学,第二节课会做的同学每人又教会了同样多的同学,这样全班共有36名同学会做这项实验.求每节课每名同学教会多少名同学做实验?
20.(8分)(23-24八年级下·福建福州·阶段练习)公安部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定. 某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售1500个,6月份销售2160个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)按照这个增长率,预计7月份该品牌头盔销售量是多少?
21.(10分)(22-23八年级下·浙江杭州·期中)如图1,有长为24米的篱笆,一面利用墙(墙的最大可用长度为15米),围成中间隔有一道篱笆的长方形花圃.
(1)如果要围成面积为36平方米的花圃,的长是多少米?
(2)如图2,如果在平行于墙面的篱笆上开两道1米宽的门,如果要围成面积为55平方米的花圃,的长时多少?
22.(10分)(23-24八年级下·浙江宁波·期中)每年的4月12日为载人空间飞行国际日,也是世界航天日.我国在2023年完成“天宫空间站”的在轨建造,取得了举世瞩目的航天成就.某商店为满足航天爱好者的需求,特推出“天宫空间站”系列A、B两款模型,A款模型比B款模型售价低20元,800元购买A款模型的数量与960元购买B款模型的数量相等.按定价销售一段时间后发现B款模型每天可以卖15件.为扩大销售,该商店准备适当降价,经过一段时间测算,B款模型每降价5元,则每天可以多卖1件.
(1)A、B两款模型每件售价分别是多少?
(2)为了使B款模型每天的销售额为1900元,而且尽可能让顾客得到实惠,求B款模型的降价后的售价为多少元/件?
23.(10分)(23-24八年级下·浙江杭州·期中)东新社区为了解决社区停车难的问题,利用一块矩形空地建了一个小型体车场,其布局如图所示,已知,,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x米的道路.已知铺花砖的面积(即阴影面积)为.
(1)求道路的宽是多少米?
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10120元,同时尽可能让利于居民?
24.(12分)(2024·山东德州·一模)为了节约用水,不少城市对用水大户作出了两段收费的规定,某市规定:月用水量不超过规定标准吨时,按每吨1.6元的价格交费,如果超过了标准,超标部分每吨还要加收元的附加费用.据统计,某户7、8两月的用水量和交费情况如下表:
月份 用水量(吨) 交费总数(元)
7 140 264
8 95 152
(1)求出该市规定标准用水量的值;
(2)当用水量超过标准吨时,写出交费总数(元)与用水量(吨)的函数关系式,并利用函数关系计算,当某月份用水量为150吨时,应交水费多少元?
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查一元二次方程的实际应用,理解题意找出等量关系是解题关键.设这种植物每个支干长出的小分支个数是x,根据题意可列出关于x的方程,再求解即可.
【详解】解:设这种植物每个支干长出的小分支个数是x,
依题意得:,
解得:(不合题意,舍去),,
∴这种植物每个支干长出的小分支个数是8.
故选:C.
2.C
【分析】本题考查了一元二次方程的应用,设十位上的数字为,则个位上的数字为,根据“一个两位数等于它的个位数的平方”列出一元二次方程,解方程即可得出答案,理解题意,找准等量关系,正确列出方程是解此题的关键.
【详解】解:设十位上的数字为,则个位上的数字为,
由题意得:,
整理得:,
解得:或,
当时,,此时这个两位数为,
当时,,此时这个两位数为,
综上所述,这个两位数为25或36,
故选:C.
3.B
【分析】本题主要考查一元二次方程的应用,熟练掌握一元二次方程的应用是解题的关键.
设该村水稻亩产量年平均增长率为,根据题意列出方程即可.
【详解】解:根据题意得:.
故选:B.
4.C
【分析】本题考查列一元二次方程解实际应用题.将三条路平移,草坪是一个长方形,如图所示,根据剩余的空地上种植草坪,使草坪的面积为,设道路的宽为,利用长方形面积公式得到,从而确定答案.
【详解】解:将三条路平移,如图所示:
剩余的空地上种植草坪,使草坪的面积为,设道路的宽度,
,
故选:C.
5.D
【分析】本题主要考查了由实际问题抽象出一元二次方程,设该款大礼包每盒降价元,根据题意列出一元二次方程,即可求解.
【详解】若设该款大礼包每盒降价元,则可列方程为
故选:D.
6.B
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.当运动时间为t秒时,,根据的面积为,即可得出关于t的一元二次方程,解之即可得出t的值.
【详解】解:当运动时间为t秒时,,
依题意得:
,
整理得:,
解得:.
故选:B.
7.C
【分析】本题考查一元二次方程的实际应用,利用互赠的数量加上老师赠送的数量等于总数量,列出方程即可.
【详解】解:设班级有x名学生,由题意,得:;
故选C.
8.D
【分析】本题考查了一元二次方程的应用,设售价为x元/台,根据利润销售量每台风扇的利润,列方程即可.
【详解】解:设售价为x元/台,
根据题意可得:,
故选:D.
9.A
【分析】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.设一瓶电热蚊香液的进价为x元,则电热蚊香液的售价为元,则一套驱蚊器的售价为6x元,进价为元,列出方程解出即可;
【详解】解:设一瓶电热蚊香液的进价为x元,则电热蚊香液的售价为元,则一套驱蚊器的售价为6x元,进价为元,由题意得:
,
解得:x=5,
所以一套驱蚊器的售价为:5×6=30(元),一套驱蚊器的利润元
设每套驱蚊器降价a元,由题意得:
,
解得: , (舍去),
故选:A.
10.A
【分析】本题主要考查一元二次方程的应用---增长率问题,根据增长率模型可逐项分析各选项进行判断即可得出结论.
【详解】解:①设甲种设备的生产成本年平均下降率为x,根据题意得:
解得,(舍去)
所以,甲种设备的生产成本年平均下降率为,①正确;
②设乙种设备的生产成本年平均下降率为y,根据题意得:
解得,(舍去)
所以,乙种设备的生产成本年平均下降率为,
即甲、乙两种设备的生产成本年平均下降率相同,②错误;
③2013年甲种设备平均每台的生产成本为,③错误;
④若乙种设备生产成本的年平均下降率不变,则估计2016年,乙种设备每台的生产成本为元,④是正确的.
综上,正确的结论是①④,
故选:A.
11.31
【分析】设九年级(4)班的同学共有x名,根据题意可得,解方程求解即可.
【详解】设九年级(4)班的同学共有x名,
依题意得:,
整理得:,
解得:(不符合题意,舍去),
∴九年级(4)班的同学共有31名.
故答案为:31.
【点睛】本题考查了一元二次方程的应用—传播问题,准确理解题意,熟练掌握知识点是解题的关键.
12.
【分析】本题考查了一元二次方程的应用中的增长率问题,找到关键描述语,就能找到等量关系,是解决问题的关键.主要考查增长率问题,一般用增长后的量=增长前的量增长率,用x表示4月 13 日的营业额即可得解.
【详解】解:依题意得4月 13 日的营业额,
∴.
故答案为:.
13./
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
设背景墙边框的宽度为,可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【详解】解:设背景墙边框的宽度为,得
解得(舍)
故答案为:.
14. 60
【分析】(1)设关于的函数关系式为,用待定系数法列方程组求解即可;
(2)根据利润=(售价-进价)×销量,列出方程求解即可得到答案.
【详解】解:(1)设关于的函数关系式为,
由图可知,点,在,
,
解得,
关于的函数关系式为,
故答案为;
(2)根据题意可得:
,
解得:或,
让利于顾客,
,
板栗的销售单价应定为60元,
故答案为:60.
【点睛】本题考查了一次函数和一元二次方程的应用,解题的关键是读懂题意,列出函数关系式和方程解决问题.
15.
【分析】本题考查了一元二次方程的实际应用,设“衰分比”为x,则乙获得奖金,丙获得奖金,根据甲、乙、丙共获得奖金175万元,列出方程求解,根据实际选择适合的值即可.
【详解】解:设“衰分比”为x,则乙获得奖金,丙获得奖金,
根据题意得:,
解得:或(舍去,不符合实际),
“衰分比”是,
故答案为:.
16.
【分析】本题考查了与图形有关的一元二次方程的应用,等腰三角形的性质,直角三角形的性质,读懂题意列出方程是关键.由等腰三角形的性质及平行条件,得点D是的中点,则,从而可表示出、,由面积关系建立方程即可.
【详解】解:∵是等腰直角三角形,,
∴,;
∵,
∴,
∴,
∴;
∵,点在上,
∴,
∴;
∵,
∴,
∴,
∴;
∵
∴.
故答案为:.
17.
【分析】根据某超市对一款原价位元的商品降价销售一段时间后,为了加大促销力度,再次降价,此时售价降低了元,列方程即可得到结论.
【详解】解:由题意得:,
故答案为:.
【点睛】此题考查了由实际问题抽象出一元二次方程,正确理解题意是解题的关键.
18.或18
【分析】本题考查一元二次方程在几何中的应用,根据移动时间为秒,分以下两种情况讨论,①当在上时,②当在上时,根据这两种情况分别用表示出和的底和高,根据建立方程求解,即可解题.
【详解】解:移动时间为秒,正方形的边长为10厘米,厘米,
①当在上时,
有厘米,厘米,厘米,
,
,即,
整理得,解得(不合题意,舍去),.
②当在上时,
则厘米,厘米,
,
整理得,解得,(不符合题意,舍去),
综上所述,的值为或18.
故答案为:或18.
19.5
【分析】此题主要考查了一元二次方程的应用,根据题意表示出两节课教会的人数是解题关键.
设平均每节课一人教会x人,第一节课后会做的有人,第二节课教会人,会做的有人,据此列方程求解即可.
【详解】解:设每节课一人教会x人,根据题意可得:
,
解得:(不合题意舍去)
答:每节课一人教会5人.
20.(1)
(2)2592
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设该品牌头盔销售量的月增长率为x,根据题意列出一元二次方程求解即可;
(2)根据题意列式计算即可.
【详解】(1)解:设该品牌头盔销售量的月增长率为x,
依题意,得:,
解得:,(不合题意,舍去).
∴该品牌头盔销售量的月增长率为;
(2)(个).
∴预计7月份该品牌头盔销售量是2592个.
21.(1)的长是米
(2)的长是米或米
【分析】本题主要考查了一元二次方程的实际应用,利用长方形的面积运算方法列出方程是解题的关键.
(1)设的长为米,则的长为米,根据长方形的面积=长宽列出方程运算即可;
(2)设的长为米,则的长为米,根据长方形的面积=长宽列出方程运算即可.
【详解】(1)解:设的长为米,则的长为米,
根据题意得:,
解得,,
当时,,不符合题意,
当时,,符合题意,
∴的长是6米;
(2)设的长为米,则的长为米,
根据题意得:,
解得,,
当时,,符合题意,
当m=6时,,符合题意,
∴的长是米或米.
22.(1)A模型每件售价100元,B模型每件售价120元
(2)95元
【分析】本题主要考查了分式方程的应用,一元二次方程的应用,
(1)根据800元购买A款模型的数量等于960元购买B款模型的数量列出分式方程,求出解即可;
(2)根据销售量乘以单价等于销售额列出一元二次方程,根据让顾客得到实惠求出解即可.
【详解】(1)解:设A模型每件售价x元,根据题意,得
∴
解得,
经检验:是方程的解,
∴,
答:A模型每件售价100元,B模型每件售价120元;
(2)解:设B模型每件下降元,根据题意,得
∴,
解得,,
∵尽可能实惠,
∴,
∴,
答:实际售价应为95元.
23.(1)米
(2)上涨元
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)道路的宽为米,根据铺花砖的面积 (即阴影面积)为 ,结合其布局图,列出一元二次方程,解方程取符合题意的值即可;
(2)设每个车位的月租金上涨元时,停车场的月租金收入为元,根据“该停车场共有车位个,据调查分析,当每个车位的月租金为元时,可全部租出;若每个车位的月租金每上涨元,就会少租出个车位”,列出一元二次方程,解方程取尽可能让利于居民的值即可.
【详解】(1)道路的宽为米,
由题意得:
整理得:
解得: (不合题意,舍去),
答:道路的宽是米;
(2)设每个车位的月租金上涨元时,停车场的月租金收入元,
由题意得:,
整理得:,
解得:,
∵尽可能让利于居民,
,
答:每个车位的月租金上涨元时,停车场的月租金收入为元.
24.(1)
(2),290元
【分析】本题考查了一元二次方程的应用、一次函数的应用,理解题意,正确得出一元二次方程以及一次函数是解此题的关键.
(1)根据七月份用水量以及交费总数得出关于的方程,解方程即可得出答案;
(2)当,根据收费方式即可得出交费总数(元)与用水量(吨)的函数关系式,求出当的值即可得解.
【详解】(1)解:因七月份用水量为140吨,,
所以需加收:(元),
即,
解得,,
又8月份用水量为95吨,,不超标,
故答案为;
(2)解:当时,则.
∴,
用水量为150吨时,应交水费:(元).
答:当某月份用水量为150吨时,应交水费290元.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
