全等三角形的判定(SSS与SAS) 专项练习(含解析)
文档属性
| 名称 | 全等三角形的判定(SSS与SAS) 专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 04:52:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
全等三角形的判定(SSS与SAS) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级上·河南信阳·期末)如图,,,,,则的度数为( )
A. B. C. D.
2.(23-24八年级上·广西百色·期末)如图,O为的中点,若要利用“”来判定,则应补充的一个条件是( )
A. B. C. D.
3.(22-23九年级上·重庆大渡口·期末)如图,在正方形中,点分别在边上,且,连接,平分交于点G.若,则的度数为( )
A. B. C. D.
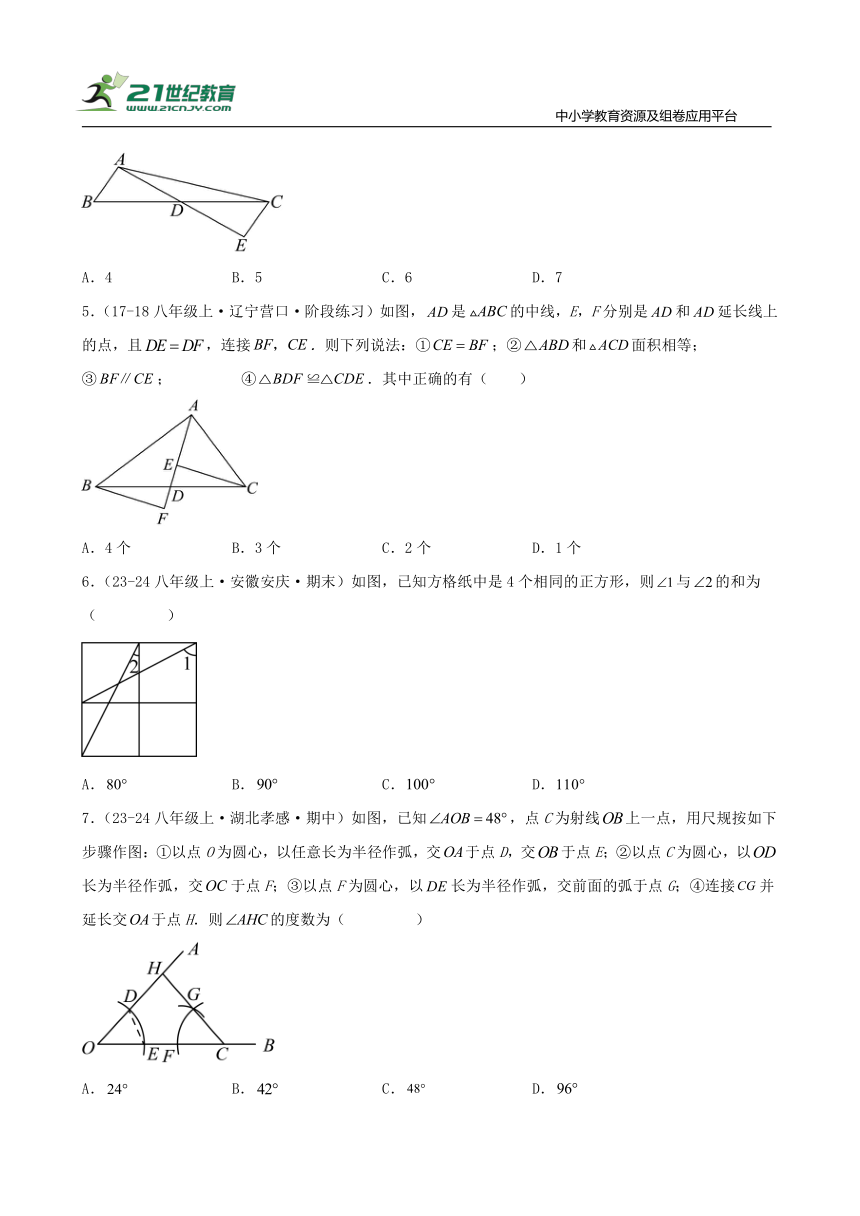
4.(2024·陕西咸阳·三模)如图,在中,为边的中点,,,延长至点,使得,则长度可以是( )
A.4 B.5 C.6 D.7
5.(17-18八年级上·辽宁营口·阶段练习)如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
6.(23-24八年级上·安徽安庆·期末)如图,已知方格纸中是4个相同的正方形,则与的和为( )
A. B. C. D.
7.(23-24八年级上·湖北孝感·期中)如图,已知,点C为射线上一点,用尺规按如下步骤作图:①以点O为圆心,以任意长为半径作弧,交于点D,交于点E;②以点C为圆心,以长为半径作弧,交于点F;③以点F为圆心,以长为半径作弧,交前面的弧于点G;④连接并延长交于点H.则的度数为( )
A. B. C. D.
8.(23-24八年级上·山东德州·阶段练习)如图,平面上有与,其中与相交于P点,如图,若,,,则的度数为( )
A. B. C. D.
9.(23-24七年级下·山西太原·阶段练习)如图1,两个大小不同的三角板叠放在一起,图2是由它得到的抽象几何图形,已知,,,且点,,在同一条直线上,,,连接.现有一只壁虎以的速度沿的路线爬行,则壁虎爬到点所用的时间为( )
A. B. C. D.
10.(21-22八年级上·云南昭通·期末)如图,是的中线,E,F分别是和延长线上的点,且,连接,下列说法:
①;
②和面积相等;
③;
④;
⑤.
其中正确的有( )
A.1个 B.5个 C.3个 D.4个
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·江苏南京·期末)如图,已知,要用“”判定,则需要补充的一个条件为 .
12.(23-24八年级上·河北保定·期末)如图,在与中,E在 边上,,,,若,则 .
13.(23-24八年级上·吉林松原·期中)如图,为了测量A、B两点之间的距离,在地面上找到一点C,使,然后在的延长线上确定点D,使,那么只要测量出的长度就得到A、B两点之间的距离,其中的依据是 .
14.(23-24八年级上·重庆江津·期中)如图,,,,若,则 .
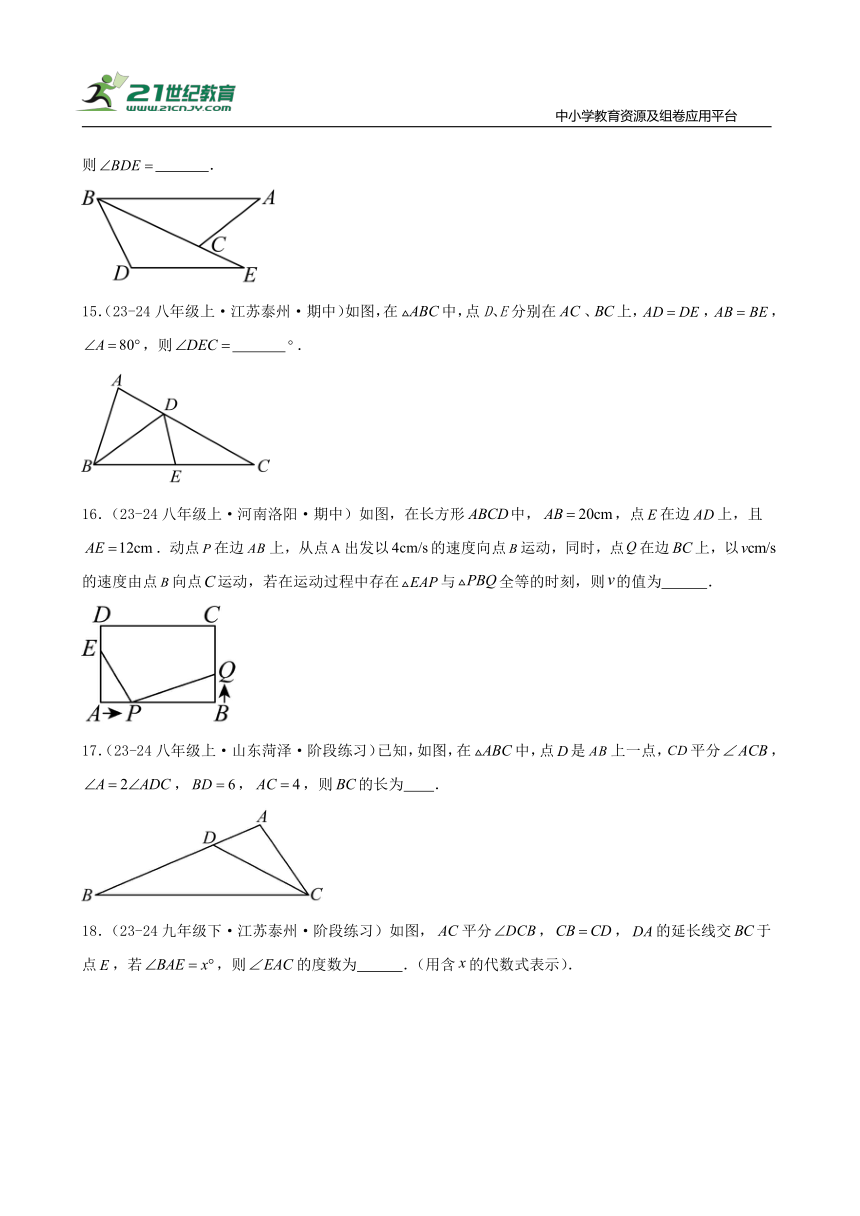
15.(23-24八年级上·江苏泰州·期中)如图,在中,点D、E分别在、上,,,,则 .
16.(23-24八年级上·河南洛阳·期中)如图,在长方形中,,点在边上,且.动点在边上,从点出发以的速度向点运动,同时,点在边上,以的速度由点向点运动,若在运动过程中存在与全等的时刻,则的值为 .
17.(23-24八年级上·山东菏泽·阶段练习)已知,如图,在中,点是上一点,平分,,,,则的长为 .
18.(23-24九年级下·江苏泰州·阶段练习)如图,平分,,的延长线交于点,若,则的度数为 .(用含的代数式表示).
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24八年级上·陕西商洛·阶段练习)如图,在和中,,且点在同一条直线上.求证:.
20.(8分)(23-24八年级上·江苏泰州·期中)如图,点在一条直线上,,交于点.
(1)求证:;
(2)求证:互相平分.
21.(10分)(23-24八年级上·天津宁河·期中)如图,已知 连接.
(1)求证: ;
(2)若 求的度数.
22.(10分)(23-24七年级下·陕西西安·阶段练习)如图,在中,D为上一点,E为中点,连接并延长至点F使得,连.
(1)求证:;
(2)若,连接,平分,求的度数.
23.(10分)(23-24七年级下·陕西西安·阶段练习)已知等腰三角形,,为射线上一动点,连接,以为边在直线的右侧作等腰三角形,,,连接.
(1)如图1,当点在边上时,请探究,,之间的数量关系.
(2)如图2,当点在的延长线上时,(1)中,,之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请你写出新的结论,并说明理由.
24.(12分)(23-24七年级下·陕西咸阳·阶段练习)如图,在中,是边上的中线,分别以,为直角边作直角和,其中,,,,连接,延长至点,使,连接.
【初步探索】(1)试说明:;
【衍生拓展】(2)探究和之间的数量关系,并说明理由.
参考答案:
1.A
【分析】本题主要考查了全等三角形的性质,正确判断对应角,对应边是解决本题的关键.在中,根据三角形内角和定理求得,根据全等三角形的对应角相等即可解决.
【详解】解:在中,,
∵,,,
∴,
∴.
故选:A.
2.D
【分析】本题主要考查了添加一个条件,使得用“”来判定,根据已知条件得出,,故只需要即可使用证明.
【详解】解:∵O为的中点,
∴,
∵,
∴当添加时,.
故选:D.
3.B
【分析】可以先证明,则,利用角平分线可得,再利用直角三角形的两锐角互余解题即可.
【详解】解:∵正方形
∴
在和中,
,
∴
∴
∵平分
∴
∴
故选B.
【点睛】本题考查正方形的性质,全等三角形的性质和判定,掌握全等三角形的判定方法是解题的关键.
4.A
【分析】本题考查了全等三角形的判定与性质,三角形三边关系;证明,得,在中由三边不等关系确定的取值范围,根据范围即可完成求解.
【详解】解:为边的中点,
;
在与中,
,
,
;
,,
,
故可以为4,
故选:A.
5.D
【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
根据三角形中线的定义可得,然后利用“”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确;
∴,故①正确,
∴,故③正确;
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的是①②③④,共4个.
故选:D.
6.B
【分析】本题考查了全等三角形的判定与性质,互余.解题的关键在于对知识的熟练掌握与灵活运用.如图,证明,则,由,可得,然后作答即可.
【详解】解:如图,
∵,,,
∴,
∴,
∵,
∴,
故选:B.
7.D
【分析】本题考查尺规基本作图-作一角等于已知角,三角形全等的判定和性质,三角形外角的性质,
根据作图,由全等三角形的判定定理可以推知,得到,即,再利用三角形外角性质求解即可.
【详解】解:由作图可知,在与中,
,
则.
∴,即,
∴.
故选:D.
8.C
【分析】易证,由全等三角形的性质可知:,再根据已知条件和四边形的内角和为,即可求出的度数.
【详解】解:在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出.
9.C
【分析】先根据等腰直角三角形的性质可以得出,属于手拉手型全等,所以,最后根据时间路程速度即可解答.本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
【详解】解:,
,
,
在与中,
,
,
,
则
壁虎以的速度B处往处爬,
.
故选:C.
10.B
【分析】根据三角形中线的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确
∴,故①正确,
∵,
∴,故⑤正确,
∴,故③正确,
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的有5个,
故选:B.
【点睛】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定方法并准确识图是解题的关键.
11.
【分析】本题主要考查对全等三角形的判定的理解和掌握,根据用“”判定,已知及公共边,添加的条件是.
【详解】解:添加的条件是,
理由是:在与中,
,
∴,
故答案为:.
12./度
【分析】本题主要考查了全等三角形的性质与判定,三角形内角和定理,证明得到,再根据三角形内角和定理和平角的定义可得.
【详解】解:∵,,,
∴,
∴,
∵,
∴,
故答案为:.
13./边角边
【分析】本题考查了全等三角形的判定,根据即可证明是解题的关键.
【详解】解:,
,
在和中,
,
,
故答案为:.
14./117度
【分析】本题考查了全等三角形的判定及其性质等知识,根据平行线的性质得出,进而利用证明和全等,利用全等三角形的性质解答即可.
【详解】解:∵,
,
在和中,
,
,
,
,
故答案为:.
15.100
【分析】本题考查了三角形全等的判定与性质,熟练掌握三角形全等的判定方法是解题关键.先证出,再根据全等三角形的性质可得,由此即可得.
【详解】解:在和中,
,
,
,
,
故答案为:100.
16.4或
【分析】本题主要考查三角形全等的判定.
设运动,则,,,由于在长方形中,,因此①当,时,,②当,时,,代入即可求解v的值.
【详解】设运动,则,,,
∵在长方形中,,
∴①当,,即,时,,
解得:,
或当,,即,时,,
解得:,.
综上所述,v的值为4或.
故答案为:4或
17.10
【分析】本题考查了全等三角形的判定与性质,解决本题的关键是证明,在边上取点,使,连接,证明,再根据已知条件证得,即可得解.
【详解】解:如图,在边上取点,使,连接,
∵平分,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴.
故答案为:10.
18.
【分析】本题主要考查了全等三角形的判定与性质,角平分线的性质,利用证明得, 根据三角形的外角定理推出, 进而根据三角形内角和定理即可求解,解题的关键是利用证明.
【详解】解:∵平分,
∴,
在和中
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
19.见解析
【分析】由可得,然后利用证明即可证明结论.
【详解】解:∵,
∴,
即,
在和中
,
∴,
∴.
【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.
20.(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定与性质,解题的关键是:
(1)利用证明,然后根据全等三角形的性质即可得证;
(2)利用证明,然后根据全等三角形的性质即可得证.
【详解】(1)证明:∵,
∴,
在和中
,
∴,
∴;
(2)证明:在和中
,
∴,
∴,,
即,互相平分.
21.(1)见解析
(2)
【分析】本题主要考查了全等三角形的判定与性质;
(1)根据题意由,可得,即可求证;
(2)由,可得,再由内角和为即可求解.
【详解】(1)证明:∵,
∴,
∴,
又∵,
∴;
(2)∵,
∴,
∵,
∴,
∴.
22.(1)见详解
(2)
【分析】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点,能综合运用定理进行推理是解此题的关键.
(1)求出,根据全等三角形的性质得出,根据平行线的判定得出即可;
(2)根据(1)求出,根据三角形内角和定理求出即可.
【详解】(1)证明:∵为中点,
,
在和中
,
,
,
;
(2)解:∵平分,
,
,
,
,
,
.
23.(1)
(2)不成立.
【分析】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定方法是解本题的关键.
(1)证明.再证明,可得,再进一步可得结论;
(2)证明.再证明,可得,再进一步可得结论;
【详解】(1)解:∵,
∴,
即.
在与中,,
∴,
∴,
∴.
(2)不成立..
理由:∵,
∴.
在与中,
,
∴,
∴.
24.(1)见解析(2),理由见解析
【分析】本题考查了全等三角形的判定和性质、平行线的判定和性质,熟练掌握知识点、推理证明是解题的关键.
(1)根据是边的中线,得出,利用证明,得出,根据“内错角相等,两直线平行”,即可证明;
(2)由(1)得,,得出,,推出,,利用证明,得出,根据,,得出,即可证明.
【详解】解:(1)∵是边的中线,
∴,
在和中,
,
∴,
∴,
∴;
(2),理由如下,
∵由(1)得,,
∴,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴.
全等三角形的判定(SSS与SAS) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级上·河南信阳·期末)如图,,,,,则的度数为( )
A. B. C. D.
2.(23-24八年级上·广西百色·期末)如图,O为的中点,若要利用“”来判定,则应补充的一个条件是( )
A. B. C. D.
3.(22-23九年级上·重庆大渡口·期末)如图,在正方形中,点分别在边上,且,连接,平分交于点G.若,则的度数为( )
A. B. C. D.
4.(2024·陕西咸阳·三模)如图,在中,为边的中点,,,延长至点,使得,则长度可以是( )
A.4 B.5 C.6 D.7
5.(17-18八年级上·辽宁营口·阶段练习)如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
6.(23-24八年级上·安徽安庆·期末)如图,已知方格纸中是4个相同的正方形,则与的和为( )
A. B. C. D.
7.(23-24八年级上·湖北孝感·期中)如图,已知,点C为射线上一点,用尺规按如下步骤作图:①以点O为圆心,以任意长为半径作弧,交于点D,交于点E;②以点C为圆心,以长为半径作弧,交于点F;③以点F为圆心,以长为半径作弧,交前面的弧于点G;④连接并延长交于点H.则的度数为( )
A. B. C. D.
8.(23-24八年级上·山东德州·阶段练习)如图,平面上有与,其中与相交于P点,如图,若,,,则的度数为( )
A. B. C. D.
9.(23-24七年级下·山西太原·阶段练习)如图1,两个大小不同的三角板叠放在一起,图2是由它得到的抽象几何图形,已知,,,且点,,在同一条直线上,,,连接.现有一只壁虎以的速度沿的路线爬行,则壁虎爬到点所用的时间为( )
A. B. C. D.
10.(21-22八年级上·云南昭通·期末)如图,是的中线,E,F分别是和延长线上的点,且,连接,下列说法:
①;
②和面积相等;
③;
④;
⑤.
其中正确的有( )
A.1个 B.5个 C.3个 D.4个
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·江苏南京·期末)如图,已知,要用“”判定,则需要补充的一个条件为 .
12.(23-24八年级上·河北保定·期末)如图,在与中,E在 边上,,,,若,则 .
13.(23-24八年级上·吉林松原·期中)如图,为了测量A、B两点之间的距离,在地面上找到一点C,使,然后在的延长线上确定点D,使,那么只要测量出的长度就得到A、B两点之间的距离,其中的依据是 .
14.(23-24八年级上·重庆江津·期中)如图,,,,若,则 .
15.(23-24八年级上·江苏泰州·期中)如图,在中,点D、E分别在、上,,,,则 .
16.(23-24八年级上·河南洛阳·期中)如图,在长方形中,,点在边上,且.动点在边上,从点出发以的速度向点运动,同时,点在边上,以的速度由点向点运动,若在运动过程中存在与全等的时刻,则的值为 .
17.(23-24八年级上·山东菏泽·阶段练习)已知,如图,在中,点是上一点,平分,,,,则的长为 .
18.(23-24九年级下·江苏泰州·阶段练习)如图,平分,,的延长线交于点,若,则的度数为 .(用含的代数式表示).
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24八年级上·陕西商洛·阶段练习)如图,在和中,,且点在同一条直线上.求证:.
20.(8分)(23-24八年级上·江苏泰州·期中)如图,点在一条直线上,,交于点.
(1)求证:;
(2)求证:互相平分.
21.(10分)(23-24八年级上·天津宁河·期中)如图,已知 连接.
(1)求证: ;
(2)若 求的度数.
22.(10分)(23-24七年级下·陕西西安·阶段练习)如图,在中,D为上一点,E为中点,连接并延长至点F使得,连.
(1)求证:;
(2)若,连接,平分,求的度数.
23.(10分)(23-24七年级下·陕西西安·阶段练习)已知等腰三角形,,为射线上一动点,连接,以为边在直线的右侧作等腰三角形,,,连接.
(1)如图1,当点在边上时,请探究,,之间的数量关系.
(2)如图2,当点在的延长线上时,(1)中,,之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请你写出新的结论,并说明理由.
24.(12分)(23-24七年级下·陕西咸阳·阶段练习)如图,在中,是边上的中线,分别以,为直角边作直角和,其中,,,,连接,延长至点,使,连接.
【初步探索】(1)试说明:;
【衍生拓展】(2)探究和之间的数量关系,并说明理由.
参考答案:
1.A
【分析】本题主要考查了全等三角形的性质,正确判断对应角,对应边是解决本题的关键.在中,根据三角形内角和定理求得,根据全等三角形的对应角相等即可解决.
【详解】解:在中,,
∵,,,
∴,
∴.
故选:A.
2.D
【分析】本题主要考查了添加一个条件,使得用“”来判定,根据已知条件得出,,故只需要即可使用证明.
【详解】解:∵O为的中点,
∴,
∵,
∴当添加时,.
故选:D.
3.B
【分析】可以先证明,则,利用角平分线可得,再利用直角三角形的两锐角互余解题即可.
【详解】解:∵正方形
∴
在和中,
,
∴
∴
∵平分
∴
∴
故选B.
【点睛】本题考查正方形的性质,全等三角形的性质和判定,掌握全等三角形的判定方法是解题的关键.
4.A
【分析】本题考查了全等三角形的判定与性质,三角形三边关系;证明,得,在中由三边不等关系确定的取值范围,根据范围即可完成求解.
【详解】解:为边的中点,
;
在与中,
,
,
;
,,
,
故可以为4,
故选:A.
5.D
【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
根据三角形中线的定义可得,然后利用“”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确;
∴,故①正确,
∴,故③正确;
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的是①②③④,共4个.
故选:D.
6.B
【分析】本题考查了全等三角形的判定与性质,互余.解题的关键在于对知识的熟练掌握与灵活运用.如图,证明,则,由,可得,然后作答即可.
【详解】解:如图,
∵,,,
∴,
∴,
∵,
∴,
故选:B.
7.D
【分析】本题考查尺规基本作图-作一角等于已知角,三角形全等的判定和性质,三角形外角的性质,
根据作图,由全等三角形的判定定理可以推知,得到,即,再利用三角形外角性质求解即可.
【详解】解:由作图可知,在与中,
,
则.
∴,即,
∴.
故选:D.
8.C
【分析】易证,由全等三角形的性质可知:,再根据已知条件和四边形的内角和为,即可求出的度数.
【详解】解:在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出.
9.C
【分析】先根据等腰直角三角形的性质可以得出,属于手拉手型全等,所以,最后根据时间路程速度即可解答.本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
【详解】解:,
,
,
在与中,
,
,
,
则
壁虎以的速度B处往处爬,
.
故选:C.
10.B
【分析】根据三角形中线的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确
∴,故①正确,
∵,
∴,故⑤正确,
∴,故③正确,
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的有5个,
故选:B.
【点睛】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定方法并准确识图是解题的关键.
11.
【分析】本题主要考查对全等三角形的判定的理解和掌握,根据用“”判定,已知及公共边,添加的条件是.
【详解】解:添加的条件是,
理由是:在与中,
,
∴,
故答案为:.
12./度
【分析】本题主要考查了全等三角形的性质与判定,三角形内角和定理,证明得到,再根据三角形内角和定理和平角的定义可得.
【详解】解:∵,,,
∴,
∴,
∵,
∴,
故答案为:.
13./边角边
【分析】本题考查了全等三角形的判定,根据即可证明是解题的关键.
【详解】解:,
,
在和中,
,
,
故答案为:.
14./117度
【分析】本题考查了全等三角形的判定及其性质等知识,根据平行线的性质得出,进而利用证明和全等,利用全等三角形的性质解答即可.
【详解】解:∵,
,
在和中,
,
,
,
,
故答案为:.
15.100
【分析】本题考查了三角形全等的判定与性质,熟练掌握三角形全等的判定方法是解题关键.先证出,再根据全等三角形的性质可得,由此即可得.
【详解】解:在和中,
,
,
,
,
故答案为:100.
16.4或
【分析】本题主要考查三角形全等的判定.
设运动,则,,,由于在长方形中,,因此①当,时,,②当,时,,代入即可求解v的值.
【详解】设运动,则,,,
∵在长方形中,,
∴①当,,即,时,,
解得:,
或当,,即,时,,
解得:,.
综上所述,v的值为4或.
故答案为:4或
17.10
【分析】本题考查了全等三角形的判定与性质,解决本题的关键是证明,在边上取点,使,连接,证明,再根据已知条件证得,即可得解.
【详解】解:如图,在边上取点,使,连接,
∵平分,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴.
故答案为:10.
18.
【分析】本题主要考查了全等三角形的判定与性质,角平分线的性质,利用证明得, 根据三角形的外角定理推出, 进而根据三角形内角和定理即可求解,解题的关键是利用证明.
【详解】解:∵平分,
∴,
在和中
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
19.见解析
【分析】由可得,然后利用证明即可证明结论.
【详解】解:∵,
∴,
即,
在和中
,
∴,
∴.
【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.
20.(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定与性质,解题的关键是:
(1)利用证明,然后根据全等三角形的性质即可得证;
(2)利用证明,然后根据全等三角形的性质即可得证.
【详解】(1)证明:∵,
∴,
在和中
,
∴,
∴;
(2)证明:在和中
,
∴,
∴,,
即,互相平分.
21.(1)见解析
(2)
【分析】本题主要考查了全等三角形的判定与性质;
(1)根据题意由,可得,即可求证;
(2)由,可得,再由内角和为即可求解.
【详解】(1)证明:∵,
∴,
∴,
又∵,
∴;
(2)∵,
∴,
∵,
∴,
∴.
22.(1)见详解
(2)
【分析】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点,能综合运用定理进行推理是解此题的关键.
(1)求出,根据全等三角形的性质得出,根据平行线的判定得出即可;
(2)根据(1)求出,根据三角形内角和定理求出即可.
【详解】(1)证明:∵为中点,
,
在和中
,
,
,
;
(2)解:∵平分,
,
,
,
,
,
.
23.(1)
(2)不成立.
【分析】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定方法是解本题的关键.
(1)证明.再证明,可得,再进一步可得结论;
(2)证明.再证明,可得,再进一步可得结论;
【详解】(1)解:∵,
∴,
即.
在与中,,
∴,
∴,
∴.
(2)不成立..
理由:∵,
∴.
在与中,
,
∴,
∴.
24.(1)见解析(2),理由见解析
【分析】本题考查了全等三角形的判定和性质、平行线的判定和性质,熟练掌握知识点、推理证明是解题的关键.
(1)根据是边的中线,得出,利用证明,得出,根据“内错角相等,两直线平行”,即可证明;
(2)由(1)得,,得出,,推出,,利用证明,得出,根据,,得出,即可证明.
【详解】解:(1)∵是边的中线,
∴,
在和中,
,
∴,
∴,
∴;
(2),理由如下,
∵由(1)得,,
∴,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴.
