2023-2024学年四川省广安市华蓥中学高二(下)月考数学试卷(5月份)(含答案)
文档属性
| 名称 | 2023-2024学年四川省广安市华蓥中学高二(下)月考数学试卷(5月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 44.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 16:30:32 | ||
图片预览



文档简介
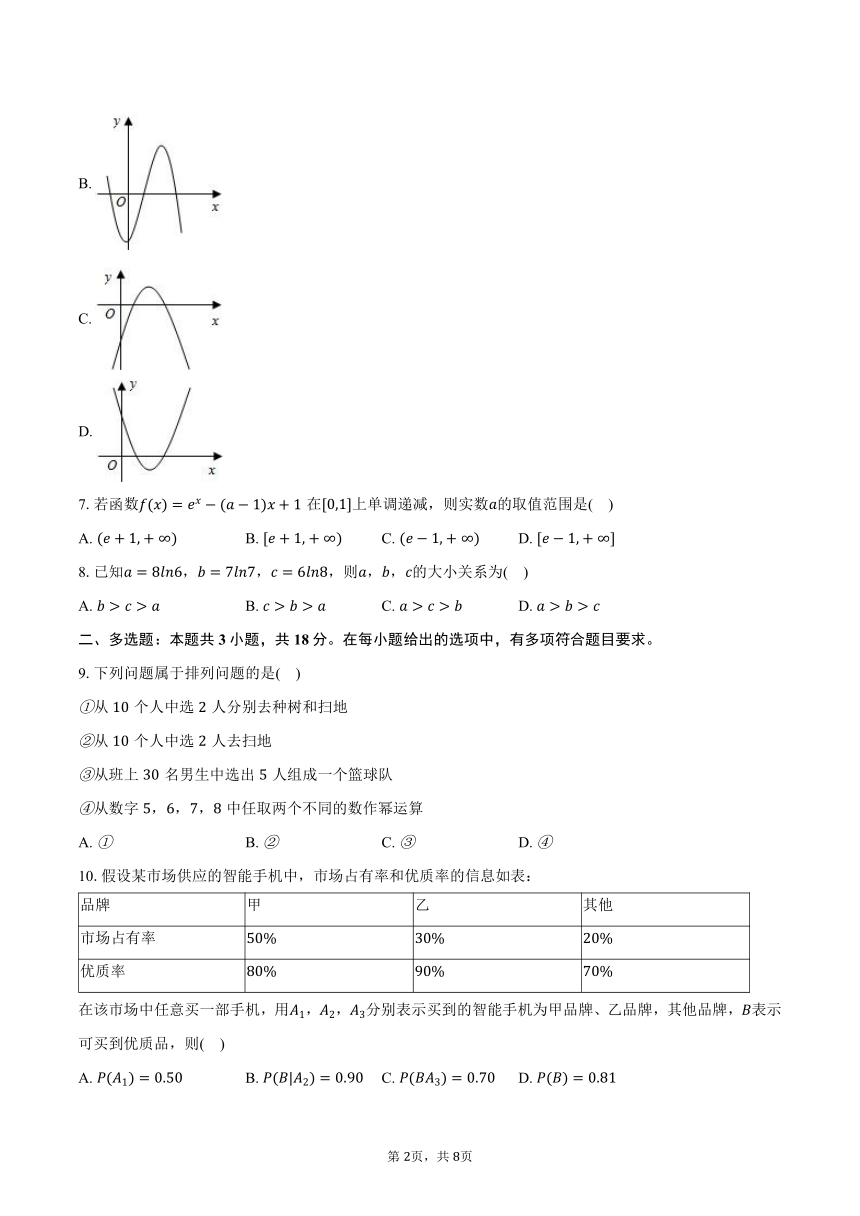
2023-2024学年四川省广安市华蓥中学高二(下)月考数学试卷(5月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知离散型随机变量的分布列如下表,则其数学期望( )
A. B. C. D.
2.红外体温计的工作原理是通过人体发出的红外热辐射来测量体温的,有一定误差用一款红外体温计测量一位体温为所示的人时,显示体温服从正态分布,若的值在内的概率约为,则的值约为( )
参考数据:若,则.
A. B. C. D.
3.若函数,则的值为( )
A. B. C. D.
4.若展开式的二项式系数之和为,则展开式的常数项为( )
A. B. C. D.
5.若,则( )
A. 或 B. C. D. 以上答案均不对
6.设函数的图象如图,则函数的图象可能是下图中的( )
A.
B.
C.
D.
7.若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
8.已知,,,则,,的大小关系为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列问题属于排列问题的是( )
从个人中选人分别去种树和扫地
从个人中选人去扫地
从班上名男生中选出人组成一个篮球队
从数字,,,中任取两个不同的数作幂运算
A. B. C. D.
10.假设某市场供应的智能手机中,市场占有率和优质率的信息如表:
品牌 甲 乙 其他
市场占有率
优质率
在该市场中任意买一部手机,用,,分别表示买到的智能手机为甲品牌、乙品牌,其他品牌,表示可买到优质品,则( )
A. B. C. D.
11.已知函数,则下列说法正确的有( )
A. 在单调递增 B. 为的一个极小值点
C. 无最大值 D. 有唯一零点
三、填空题:本题共3小题,每小题5分,共15分。
12.从台甲型彩电和台乙型彩电中任取台,若设表示所取的台彩电中甲型彩电的台数,则 ______.
13.的展开式中,含项的系数是______.
14.若函数有两个不同的极值点,则实数取值范围为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
若.
求的值;
求的值;
求的值.
16.本小题分
一组学生共有人,从中选出人参加一项活动,共有多少种选法?
有名学生参加争夺数学、物理、化学竞赛冠军,有多少种不同的结果?
书架上某层有本书,新买本插进去,要保持原有本书的顺序,有多少种不同的方法?
一组学生共有人,其中名男生和名女生,从中选出男生人,女生人,参加三项不同的活动,要求每人参加一项且每项活动都有人参加的选法有多少种?
位男生和位女生共位同学站成一排,若男生甲不站两端,位女生中有且只有两位女生相邻,有多少种不同的方法?
17.本小题分
据调查,目前对于已经近视的小学生,有两种配戴眼镜的选择,一种是佩戴传统的框架眼镜;另一种是佩戴角膜塑形镜,这种眼镜是晚上睡觉时佩戴的一种特殊的隐形眼镜因其在一定程度上可以减缓近视的发展速度,所以越来越多的小学生家长选择角膜塑形镜控制孩子的近视发展,市从该地区小学生中随机抽取容量为的样本,其中因近视佩戴眼镜的有人其中佩戴角膜塑形镜的有人,其中名是男生,名是女生.
若从样本中选一位学生,已知这位小学生戴眼镜,那么,他戴的是角膜塑形镜的概率悬多大?
从这名跟角膜塑形镜的学生中,选出个人,求其中男生人数的期望与方差;
若将样本的频率当做估计总体的概率,请问,从市的小学生中,随机选出位小学生,记其中佩戴角膜塑形镜的人数为,求恰好时的概率不用化简及的方差.
18.本小题分
已知函数.
当时,求函数在点处的切线方程;
当时,求函数的极值;
若在上是单调增函数,求实数的取值范围.
19.本小题分
已知函数.
Ⅰ当时,求的极值;
Ⅱ当时,求在上的最小值;
Ⅲ若在上存在零点,求的取值范围.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12..
13..
14..
15..解:令,则,
令,则,
令,则,
,
;
,
即为含项的系数,为,
则.
16..解:一组学生共有人,从中选出人参加一项活动,共有种选法;
争夺数学竞赛冠军有种,争夺物理竞赛冠军有种,争夺化学竞赛冠军有种,
因此共有种不同的结果;
插入第一本书,有种插法,插入第二本书,有种插法,插入第三本书,有种插法,
因此共有种不同的方法;
一组学生共有人,其中名男生和名女生,从中选出男生人,女生人,共有种选法,
再将选出的人按照人数比为::分成组,有种分法,
再将已经分好的组人分给项不同的活动,有种,所以共有种选法;
先排三位男生,有种排法,然后从三名女生中任取两名捆在一起,有种,
然后把捆在一起的整体与剩下的一名女生插入到男生旁边个位置的个位置,有种,
故位女生中有且只有两位女生相邻的排法有种,
又男生甲不在两端,其中甲在两端的情况有种,
故满足题意的排法有种.
17..解:设“这位小学生佩戴眼镜”为事件,“这位小学生佩戴的眼镜是角膜塑形镜”为事件,
所以,
所以若从样本中选一位学生,已知这位小学生戴眼镜,则他戴的是角膜塑形镜的概率是.
依题意可知:其中男生人数的所有可能取值分别为:,,,
则,,,
的分布列为:
,
.
由题意可知,
,.
18..解:当时,,定义域为,
,所以函数在点处的切线的斜率为,
又,
所以函数在点处的切线方程为,
即.
,令,解得,
当时,,当时,,
所以 在上是减函数,在上是增函数,
所以在处取得极小值是,无极大值.
因为在上是单调增函数,
所以在上恒成立,
即在上恒成立,
因为在上为单调递减函数,
所以当时,取得最大值,即,
所以.
19..解:Ⅰ当时,,定义域,,
令,则,变化时,,的变化情况如下表:
则,没有极小值;
Ⅱ当时,,定义域,
则,
令,定义域,则,
则在上是增函数,则,所以,
即在上是增函数,则;
Ⅲ,定义域:,,
令,定义域:,,
当时,由知在上是增函数,,不合题意;
当时,在上是增函数,在上是增函数,
则在上是增函数,,不合题意,
当时,,则在上是减函数,则,
当时,,则在上是减函数,,不合题意;
当时,,则存在,使,即,变化时,,的变化情况如下表:
极大值
则,只需,即,
综上,的取值范围是.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知离散型随机变量的分布列如下表,则其数学期望( )
A. B. C. D.
2.红外体温计的工作原理是通过人体发出的红外热辐射来测量体温的,有一定误差用一款红外体温计测量一位体温为所示的人时,显示体温服从正态分布,若的值在内的概率约为,则的值约为( )
参考数据:若,则.
A. B. C. D.
3.若函数,则的值为( )
A. B. C. D.
4.若展开式的二项式系数之和为,则展开式的常数项为( )
A. B. C. D.
5.若,则( )
A. 或 B. C. D. 以上答案均不对
6.设函数的图象如图,则函数的图象可能是下图中的( )
A.
B.
C.
D.
7.若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
8.已知,,,则,,的大小关系为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列问题属于排列问题的是( )
从个人中选人分别去种树和扫地
从个人中选人去扫地
从班上名男生中选出人组成一个篮球队
从数字,,,中任取两个不同的数作幂运算
A. B. C. D.
10.假设某市场供应的智能手机中,市场占有率和优质率的信息如表:
品牌 甲 乙 其他
市场占有率
优质率
在该市场中任意买一部手机,用,,分别表示买到的智能手机为甲品牌、乙品牌,其他品牌,表示可买到优质品,则( )
A. B. C. D.
11.已知函数,则下列说法正确的有( )
A. 在单调递增 B. 为的一个极小值点
C. 无最大值 D. 有唯一零点
三、填空题:本题共3小题,每小题5分,共15分。
12.从台甲型彩电和台乙型彩电中任取台,若设表示所取的台彩电中甲型彩电的台数,则 ______.
13.的展开式中,含项的系数是______.
14.若函数有两个不同的极值点,则实数取值范围为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
若.
求的值;
求的值;
求的值.
16.本小题分
一组学生共有人,从中选出人参加一项活动,共有多少种选法?
有名学生参加争夺数学、物理、化学竞赛冠军,有多少种不同的结果?
书架上某层有本书,新买本插进去,要保持原有本书的顺序,有多少种不同的方法?
一组学生共有人,其中名男生和名女生,从中选出男生人,女生人,参加三项不同的活动,要求每人参加一项且每项活动都有人参加的选法有多少种?
位男生和位女生共位同学站成一排,若男生甲不站两端,位女生中有且只有两位女生相邻,有多少种不同的方法?
17.本小题分
据调查,目前对于已经近视的小学生,有两种配戴眼镜的选择,一种是佩戴传统的框架眼镜;另一种是佩戴角膜塑形镜,这种眼镜是晚上睡觉时佩戴的一种特殊的隐形眼镜因其在一定程度上可以减缓近视的发展速度,所以越来越多的小学生家长选择角膜塑形镜控制孩子的近视发展,市从该地区小学生中随机抽取容量为的样本,其中因近视佩戴眼镜的有人其中佩戴角膜塑形镜的有人,其中名是男生,名是女生.
若从样本中选一位学生,已知这位小学生戴眼镜,那么,他戴的是角膜塑形镜的概率悬多大?
从这名跟角膜塑形镜的学生中,选出个人,求其中男生人数的期望与方差;
若将样本的频率当做估计总体的概率,请问,从市的小学生中,随机选出位小学生,记其中佩戴角膜塑形镜的人数为,求恰好时的概率不用化简及的方差.
18.本小题分
已知函数.
当时,求函数在点处的切线方程;
当时,求函数的极值;
若在上是单调增函数,求实数的取值范围.
19.本小题分
已知函数.
Ⅰ当时,求的极值;
Ⅱ当时,求在上的最小值;
Ⅲ若在上存在零点,求的取值范围.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12..
13..
14..
15..解:令,则,
令,则,
令,则,
,
;
,
即为含项的系数,为,
则.
16..解:一组学生共有人,从中选出人参加一项活动,共有种选法;
争夺数学竞赛冠军有种,争夺物理竞赛冠军有种,争夺化学竞赛冠军有种,
因此共有种不同的结果;
插入第一本书,有种插法,插入第二本书,有种插法,插入第三本书,有种插法,
因此共有种不同的方法;
一组学生共有人,其中名男生和名女生,从中选出男生人,女生人,共有种选法,
再将选出的人按照人数比为::分成组,有种分法,
再将已经分好的组人分给项不同的活动,有种,所以共有种选法;
先排三位男生,有种排法,然后从三名女生中任取两名捆在一起,有种,
然后把捆在一起的整体与剩下的一名女生插入到男生旁边个位置的个位置,有种,
故位女生中有且只有两位女生相邻的排法有种,
又男生甲不在两端,其中甲在两端的情况有种,
故满足题意的排法有种.
17..解:设“这位小学生佩戴眼镜”为事件,“这位小学生佩戴的眼镜是角膜塑形镜”为事件,
所以,
所以若从样本中选一位学生,已知这位小学生戴眼镜,则他戴的是角膜塑形镜的概率是.
依题意可知:其中男生人数的所有可能取值分别为:,,,
则,,,
的分布列为:
,
.
由题意可知,
,.
18..解:当时,,定义域为,
,所以函数在点处的切线的斜率为,
又,
所以函数在点处的切线方程为,
即.
,令,解得,
当时,,当时,,
所以 在上是减函数,在上是增函数,
所以在处取得极小值是,无极大值.
因为在上是单调增函数,
所以在上恒成立,
即在上恒成立,
因为在上为单调递减函数,
所以当时,取得最大值,即,
所以.
19..解:Ⅰ当时,,定义域,,
令,则,变化时,,的变化情况如下表:
则,没有极小值;
Ⅱ当时,,定义域,
则,
令,定义域,则,
则在上是增函数,则,所以,
即在上是增函数,则;
Ⅲ,定义域:,,
令,定义域:,,
当时,由知在上是增函数,,不合题意;
当时,在上是增函数,在上是增函数,
则在上是增函数,,不合题意,
当时,,则在上是减函数,则,
当时,,则在上是减函数,,不合题意;
当时,,则存在,使,即,变化时,,的变化情况如下表:
极大值
则,只需,即,
综上,的取值范围是.
第1页,共1页
同课章节目录
