2024年河南省中考数学试题(含答案)
文档属性
| 名称 | 2024年河南省中考数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 783.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 00:00:00 | ||
图片预览



文档简介
2024年河南省普通高中招生考试试卷
数学
注意事项:
1.本试卷共6页,三个大题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求,直接把答案填写在答题卡上。答在试卷上的答案无效。
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1.如图,数轴上点P表示的数是( )
A.-1 B.0 C.1 D.2
2.据统计,2023年我国人工智能核心产业规模达5784亿元.数据“5784亿”用科学记数法表示为( )
A. B. C. D.
3.如图,乙地在甲地的北偏东50°方向上,则∠1的度数为( )
A.60° B.50° C.40° D.30°
4.信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )
A. B.
C. D.
5.下列不等式中,与组成的不等式组无解的是( )
A. B. C. D.
6.如图,在中,对角线AC,BD相交于点O,点E为OC的中点,交BC于点F.若,则EF的长为( )
A. B.1 C. D.2
7.计算的结果是( )
A. B. C. D.
8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
9.如图,是边长为的等边三角形ABC的外接圆,点D是的中点,连接BD,CD.以点D为圆心,BD的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
10.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )
A.当P=440W时,I=2A
B.Q随I的增大而增大
C.I每增加1A,Q的增加量相同
D.P越大,插线板电源线产生的热量Q越多
二、填空题(每小题3分,共15分)
11.请写出的一个同类项:_______.
12.2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.
13.若关于的方程有两个相等的实数根,则c的值为___________.
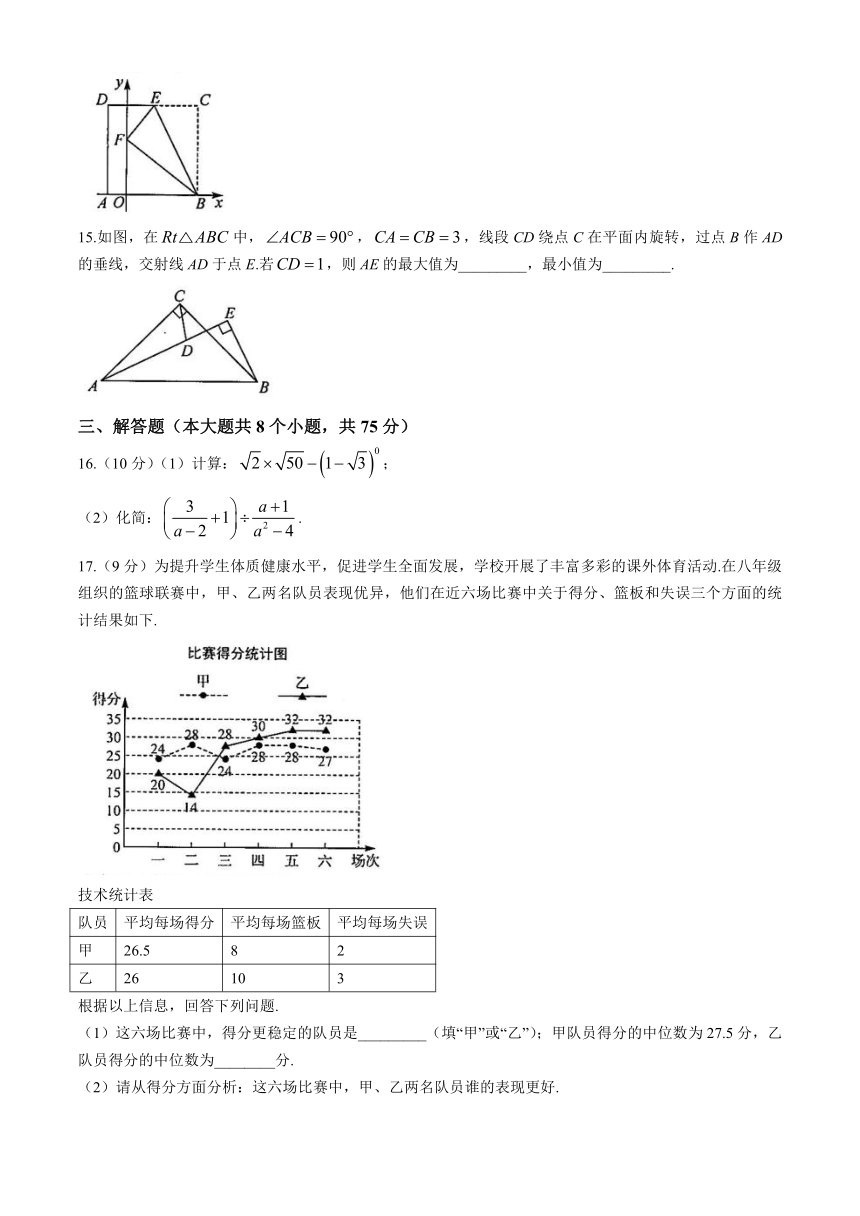
14.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上.将沿BE折登,点C落在点F处.若点F的坐标为(0,6),则点E的坐标为___________.
15.如图,在中,,,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若,则AE的最大值为_________,最小值为_________.
三、解答题(本大题共8个小题,共75分)
16.(10分)(1)计算:;
(2)化简:.
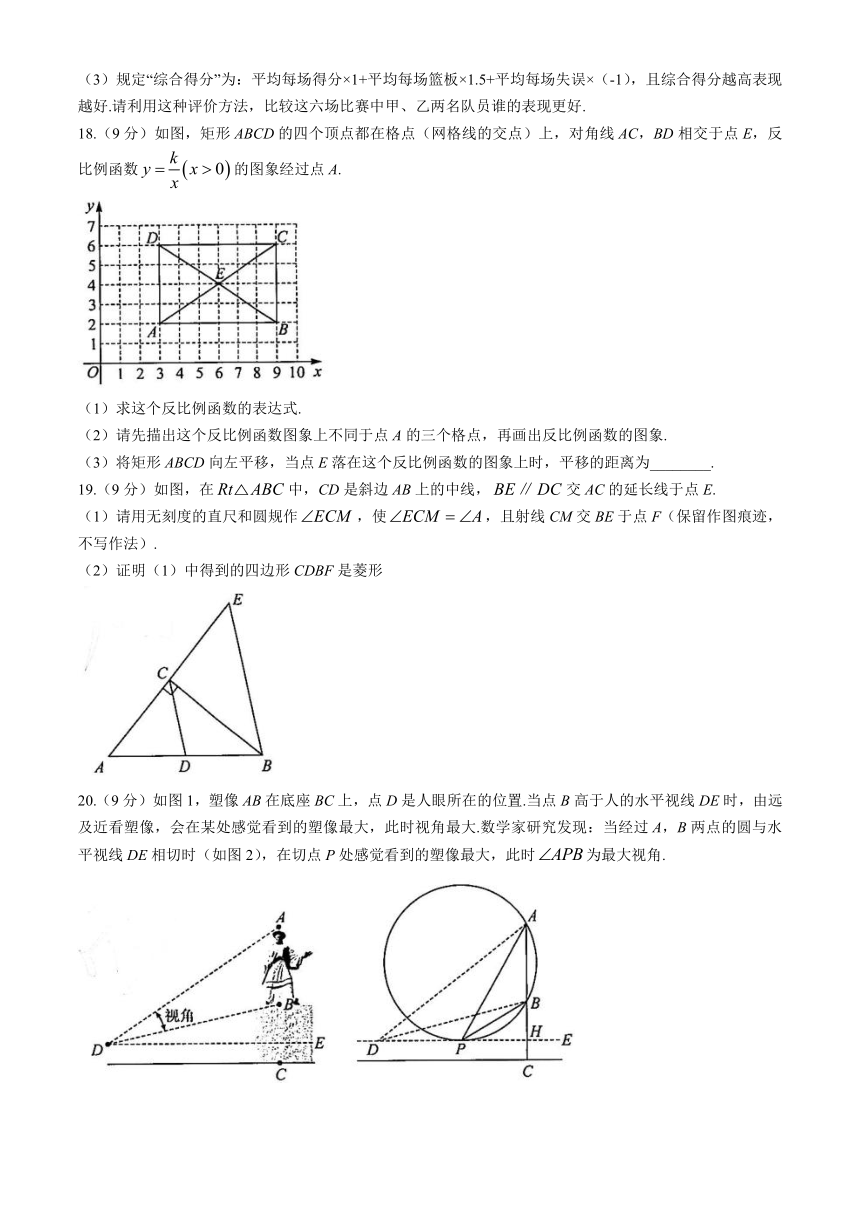
17.(9分)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
18.(9分)如图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数的图象经过点A.
(1)求这个反比例函数的表达式.
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象.
(3)将矩形ABCD向左平移,当点E落在这个反比例函数的图象上时,平移的距离为________.
19.(9分)如图,在中,CD是斜边AB上的中线,交AC的延长线于点E.
(1)请用无刻度的直尺和圆规作,使,且射线CM交BE于点F(保留作图痕迹,不写作法).
(2)证明(1)中得到的四边形CDBF是菱形
20.(9分)如图1,塑像AB在底座BC上,点D是人眼所在的位置.当点B高于人的水平视线DE时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线DE相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
图1 图2
(1)请仅就图2的情形证明.
(2)经测量,最大视角为30°,在点P处看塑像顶部点A的仰角为60°,点P到塑像的水平距离PH为6m.求塑像AB的高(结果精确到0.1m.参考数据:).
21.(9分)为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分表如下.
(1)若要从这两种食品中摄入4600kJ热量和70g蛋白质,应选用A,B两种食品各多少包
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g,且热量最低,应如何选用这两种食品
22.(10分)从地面竖直向上发射的物体离地面的高度满足关系式,其中是物体运动的时间,是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后_________s时离地面的高度最大(用含的式子表示).
(2)若小球离地面的最大高度为20m,求小球被发射时的速度.
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s.”已知实验楼高15m,请判断他的说法是否正确,并说明理由.
23.(10分)综合与实践
在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
(1)操作判断
用分别含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).
图1
(2)性质探究
根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图2,四边形ABCD是邻等对补四边形,,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若,,,求AC的长(用含m,n,的式子表示).
图2 图3
(3)拓展应用
如图3,在中,,,,分别在边BC,AC上取点M,N,使四边形ABMN是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN的长.
2024年河南省普通高中招生考试
数学试题参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A A B D D C C
二、填空题(每小题3分,共15分)
题号 11 12 13 14 15
答案 (答案不唯一) 9
三、解答题(本大题共8个小题,共75分)
16.(1)原式=10-1=9.
(2)原式.
17.(1)甲 29
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.
(3)甲的综合得分为:26.5×1+8×1.5+2×(-1)=36.5.
乙的综合得分为:26×1+10×1.5+3×(-1)=38.
因为38>36.5,所以乙队员表现更好.
18.(1)∵反比例函数的图象经过点,
∴.∴.
∴这个反比例函数的表达式为.
(2)如图
19.(1)如图.
(2)由(1),得.∴.
∵,∴四边形CDBF是平行四边形.
∵CD是斜边AB上的中线,∴.
∴是菱形.
20.(1)如图,连接BM.
则.
∵,∴.
(2)在中,,.
∵,∴.
∵,∴.
在中,,
∴.
∴.
答:塑像AB的高约为6.9m.
21.(1)设选用A种食品x包,B种食品y包,
根据题意,得
解方程组,得
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品包,则选用B种食品包,
根据题意,得.
∴.
设总热量为wkJ,则.
∵-200<0,
∴w随a的增大而减小.
∴当时,w最小.
∴.
答:选用A种食品3包,B种食品4包.
22.(1)
(2)根据题意,得
当时,.
∴.∴.
(3)小明的说法不正确.
理由如下:
由(2),得.
当时,.
解方程,得,.
∴小明的说法不正确.
23.(1)②④
(2)①.
理由如下:
延长CB至点E,使.连接AE.
∵四边形ABCD是邻等对补四边形,∴
∵,∴.
∵AB=AD,∴.
∴,.
∴.∴.
②过点A作,垂足为点F.
∵,∴.
∵,∴.
在中,,
∴.
(3)或.
数学
注意事项:
1.本试卷共6页,三个大题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求,直接把答案填写在答题卡上。答在试卷上的答案无效。
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1.如图,数轴上点P表示的数是( )
A.-1 B.0 C.1 D.2
2.据统计,2023年我国人工智能核心产业规模达5784亿元.数据“5784亿”用科学记数法表示为( )
A. B. C. D.
3.如图,乙地在甲地的北偏东50°方向上,则∠1的度数为( )
A.60° B.50° C.40° D.30°
4.信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )
A. B.
C. D.
5.下列不等式中,与组成的不等式组无解的是( )
A. B. C. D.
6.如图,在中,对角线AC,BD相交于点O,点E为OC的中点,交BC于点F.若,则EF的长为( )
A. B.1 C. D.2
7.计算的结果是( )
A. B. C. D.
8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
9.如图,是边长为的等边三角形ABC的外接圆,点D是的中点,连接BD,CD.以点D为圆心,BD的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
10.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )
A.当P=440W时,I=2A
B.Q随I的增大而增大
C.I每增加1A,Q的增加量相同
D.P越大,插线板电源线产生的热量Q越多
二、填空题(每小题3分,共15分)
11.请写出的一个同类项:_______.
12.2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.
13.若关于的方程有两个相等的实数根,则c的值为___________.
14.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上.将沿BE折登,点C落在点F处.若点F的坐标为(0,6),则点E的坐标为___________.
15.如图,在中,,,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若,则AE的最大值为_________,最小值为_________.
三、解答题(本大题共8个小题,共75分)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
18.(9分)如图,矩形ABCD的四个顶点都在格点(网格线的交点)上,对角线AC,BD相交于点E,反比例函数的图象经过点A.
(1)求这个反比例函数的表达式.
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象.
(3)将矩形ABCD向左平移,当点E落在这个反比例函数的图象上时,平移的距离为________.
19.(9分)如图,在中,CD是斜边AB上的中线,交AC的延长线于点E.
(1)请用无刻度的直尺和圆规作,使,且射线CM交BE于点F(保留作图痕迹,不写作法).
(2)证明(1)中得到的四边形CDBF是菱形
20.(9分)如图1,塑像AB在底座BC上,点D是人眼所在的位置.当点B高于人的水平视线DE时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线DE相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
图1 图2
(1)请仅就图2的情形证明.
(2)经测量,最大视角为30°,在点P处看塑像顶部点A的仰角为60°,点P到塑像的水平距离PH为6m.求塑像AB的高(结果精确到0.1m.参考数据:).
21.(9分)为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分表如下.
(1)若要从这两种食品中摄入4600kJ热量和70g蛋白质,应选用A,B两种食品各多少包
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g,且热量最低,应如何选用这两种食品
22.(10分)从地面竖直向上发射的物体离地面的高度满足关系式,其中是物体运动的时间,是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后_________s时离地面的高度最大(用含的式子表示).
(2)若小球离地面的最大高度为20m,求小球被发射时的速度.
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s.”已知实验楼高15m,请判断他的说法是否正确,并说明理由.
23.(10分)综合与实践
在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
(1)操作判断
用分别含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).
图1
(2)性质探究
根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图2,四边形ABCD是邻等对补四边形,,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若,,,求AC的长(用含m,n,的式子表示).
图2 图3
(3)拓展应用
如图3,在中,,,,分别在边BC,AC上取点M,N,使四边形ABMN是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN的长.
2024年河南省普通高中招生考试
数学试题参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A A B D D C C
二、填空题(每小题3分,共15分)
题号 11 12 13 14 15
答案 (答案不唯一) 9
三、解答题(本大题共8个小题,共75分)
16.(1)原式=10-1=9.
(2)原式.
17.(1)甲 29
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.
(3)甲的综合得分为:26.5×1+8×1.5+2×(-1)=36.5.
乙的综合得分为:26×1+10×1.5+3×(-1)=38.
因为38>36.5,所以乙队员表现更好.
18.(1)∵反比例函数的图象经过点,
∴.∴.
∴这个反比例函数的表达式为.
(2)如图
19.(1)如图.
(2)由(1),得.∴.
∵,∴四边形CDBF是平行四边形.
∵CD是斜边AB上的中线,∴.
∴是菱形.
20.(1)如图,连接BM.
则.
∵,∴.
(2)在中,,.
∵,∴.
∵,∴.
在中,,
∴.
∴.
答:塑像AB的高约为6.9m.
21.(1)设选用A种食品x包,B种食品y包,
根据题意,得
解方程组,得
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品包,则选用B种食品包,
根据题意,得.
∴.
设总热量为wkJ,则.
∵-200<0,
∴w随a的增大而减小.
∴当时,w最小.
∴.
答:选用A种食品3包,B种食品4包.
22.(1)
(2)根据题意,得
当时,.
∴.∴.
(3)小明的说法不正确.
理由如下:
由(2),得.
当时,.
解方程,得,.
∴小明的说法不正确.
23.(1)②④
(2)①.
理由如下:
延长CB至点E,使.连接AE.
∵四边形ABCD是邻等对补四边形,∴
∵,∴.
∵AB=AD,∴.
∴,.
∴.∴.
②过点A作,垂足为点F.
∵,∴.
∵,∴.
在中,,
∴.
(3)或.
同课章节目录
