2024年天津市中考数学试题(图片版,含答案)
文档属性
| 名称 | 2024年天津市中考数学试题(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 938.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 23:10:35 | ||
图片预览




文档简介
机密★启用前
2024 年天津市初中学业水平考试试卷
数 学
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷为第 1 页至第 3
页,第Ⅱ卷为第 4 页至第 8 页。试卷满分 120 分。考试时间 100 分钟。
答卷前,请务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”
上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案
答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。
祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用 2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共 12 题,共 36 分。
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分. 在每小题给出的四个选项中,
只有一项是符合题目要求的)
(1)计算3 ( 3)的结果等于
(A) 6 (B) 0
(C)3 (D) 6
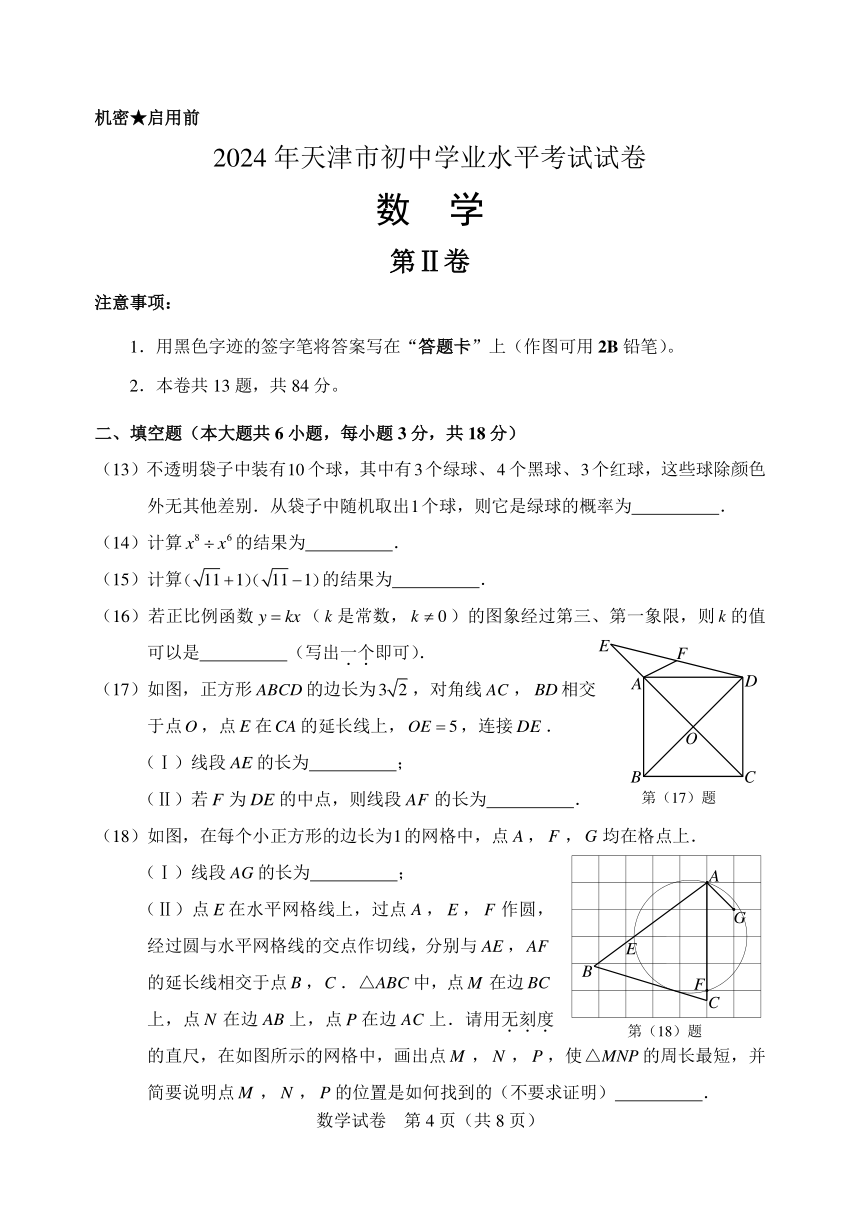
(2)右图是一个由5个相同的正方体组成的立体图形,它的主视图是
(A) (B)
第(2)题
(C) (D)
数学试卷 第 1 页(共 8 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(3)估计 10 的值在
(A)1和 2 之间 (B) 2 和3之间
(C)3和 4 之间 (D) 4 和 5 之间
(4)在一些美术字中,有的汉字是轴对称图形.下面 4 个汉字中,可以看作是轴对称
图形的是
(A) (B) (C) (D)
(5)据 2024 年 4 月 18 日《天津日报》报道,天津市组织开展了第 43 届“爱鸟周”
大型主题宣传活动.据统计,今春过境我市候鸟总数已超过 800 000 只.将数据
800 000 用科学记数法表示应为
(A)0.08 107 (B)0.8 106
(C)8 105 (D)80 104
(6) 2 cos45 1的值等于
(A) 0 (B)1
2
(C) 1 (D) 2 1
2
3x 3
(7)计算 的结果等于
x 1 x 1
(A)3 (B) x
x 3
(C) (D)
x 1 x2 1
5
(8)若点 A(x , 1),B(x2 ,11 ),C(x3 ,5)都在反比例函数 y 的图象上,则 x1 , x2 ,
x
x3 的大小关系是
(A) x1 x2 x3 (B) x1 x3 x2
(C) x3 x2 x1 (D) x2 x1 x3
数学试卷 第 2 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(9)《孙子算经》是我国古代著名的数学典籍,其中有一道题:“今有木,不知长短.引
绳度之,余绳四尺五寸;屈绳度之,不足一尺.木长几何?”意思是:用一根绳子
去量一根长木,绳子还剩余 4.5 尺;将绳子对折再量长木,长木还剩余1尺.问木长
多少尺?设木长 x尺,绳子长 y 尺,则可以列出的方程组为
y x 4.5, y x 4.5,
(A) (B)
x 0.5y 1 x 0.5y 1
x y 4.5, x y 4.5,
(C) (D)
x y 1 y x 1
(10)如图, Rt△ABC 中, C 90 , B 40 ,以点 A 为圆心,适当长为半径画弧,
1
交 AB 于点 E ,交 AC 于点 F ;再分别以点 E , F 为圆心,大于 EF 的长为半径
2
画弧,两弧(所在圆的半径相等)在 BAC 的内部相交于点 P ;画射线 AP ,与 BC
C
P
相交于点 D ,则 ADC 的大小为 D
F
(A)60 (B)65
A E B
(C)70 (D)75 第(10)题
(11)如图,△ABC 中, B 30 ,将△ABC 绕点C 顺时针旋转
E
60 得到△DEC ,点 A , B 的对应点分别为 D , E ,延长 F
D
BA 交 DE 于点 F ,下列结论一定正确的是 A
(A) ACB ACD (B) AC // DE
B C
(C) AB EF (D) BF CE 第(11)题
(12)从地面竖直向上抛出一小球,小球的高度 h (单位: m)与小球的运动时间 t
(单位: s )之间的关系式是 h 30t 5t2 (0≤ t≤6).有下列结论:
① 小球从抛出到落地需要6 s ;
② 小球运动中的高度可以是 30 m ;
③ 小球运动 2 s时的高度小于运动5 s时的高度.
其中,正确结论的个数是
(A) 0 (B)1
(C) 2 (D)3
数学试卷 第 3 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
机密★启用前
2024 年天津市初中学业水平考试试卷
数 学
第Ⅱ卷
注意事项:
1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用 2B 铅笔)。
2.本卷共 13 题,共 84 分。
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
(13)不透明袋子中装有10 个球,其中有3个绿球、4 个黑球、3个红球,这些球除颜色
外无其他差别.从袋子中随机取出1个球,则它是绿球的概率为 .
(14)计算 x8 x6 的结果为 .
(15)计算( 11 1)( 11 1)的结果为 .
(16)若正比例函数 y kx ( k 是常数, k 0)的图象经过第三、第一象限,则 k 的值
可以是 (写出一.个.即可).
E
F
(17)如图,正方形 ABCD 的边长为 D3 2 ,对角线 AC , BD相交 A
于点O ,点 E 在CA 的延长线上,OE 5,连接 DE .
O
(Ⅰ)线段 AE 的长为 ;
B C
(Ⅱ)若 F 为 DE 的中点,则线段 AF 的长为 . 第(17)题
(18)如图,在每个小正方形的边长为1的网格中,点 A , F ,G 均在格点上.
(Ⅰ)线段 AG 的长为 ; A
(Ⅱ)点 E 在水平网格线上,过点 A , E , F 作圆,
G
经过圆与水平网格线的交点作切线,分别与 AE ,AF E
B
的延长线相交于点 B ,C .△ABC 中,点M 在边 BC F
C
上,点 N 在边 AB 上,点 P 在边 AC 上.请用无.刻.度. 第(18)题
的直尺,在如图所示的网格中,画出点 M , N , P ,使△MNP 的周长最短,并
简要说明点M , N , P 的位置是如何找到的(不要求证明) .
数学试卷 第 4 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
三、解答题(本大题共 7 小题,共 66 分.解答应写出文字说明、演算步骤或推理过程)
(19)(本小题 8 分)
2x 1≤3, ①
解不等式组
3x 1≥ x 7. ②
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
4 3 2 1 0 1 2
(Ⅳ)原不等式组的解集为 .
(20)(本小题 8 分)
为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级
a名学生,根据统计的结果,绘制出如下的统计图①和图②.
人数
6 h 18 17
10 h 6% 16 15
7 h
16% 14
14%
12
10
8
9 h 8 7
30% 8 h 6
m% 4 3
2
0
6 7 8 9 10 时间/ h
图① 图②
第(20)题
请根据相关信息,解答下列问题:
(Ⅰ)填空: a的值为 ,图①中 m 的值为 ,统计的这组学生
每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(Ⅱ)求统计的这组学生每周参加科学教育的时间数据的平均数;
(Ⅲ)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加
科学教育的时间是 9 h 的人数约为多少?
数学试卷 第 5 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(21)(本小题 10 分)
已知△AOB 中, ABO 30 , AB 为⊙O 的弦,直线 MN 与⊙O 相切于点C .
(Ⅰ)如图①,若 AB // MN ,直径CE 与 AB 相交于点D ,求 AOB 和 BCE 的大小;
(Ⅱ)如图②,若OB // MN ,CG AB ,垂足为G ,CG 与OB 相交于点 F ,OA 3,
求线段OF 的长.
E
A
A D B
G
O O BF
M C N M C N
图① 图②
第(21)题
(22)(本小题 10 分)
综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔 AB 的高度(如图①).
某学习小组设计了一个方案:如图②,点C , D , E 依次在同一条水平直线上,
DE 36 m , EC AB ,垂足为C .在 D 处测得桥塔顶部 B 的仰角( CDB )为 45 ,
测得桥塔底部 A的俯角( CDA)为6 ,又在E 处测得桥塔顶部B 的仰角( CEB )为31 .
(Ⅰ)求线段CD 的长(结果取整数);
(Ⅱ)求桥塔 AB 的高度(结果取整数).
参考数据: tan 31 0.6, tan 6 0.1.
B B
C E
A A D
图① 图②
第(22)题
数学试卷 第 6 页(共 8 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(23)(本小题 10 分)
已知张华的家、画社、文化广场依次在同一条直线上,画社离家 0.6 km ,文化广场
离家1.5 km .张华从家出发,先匀速骑行了 4 min 到画社,在画社停留了15 min ,之后
匀速骑行了 6 min 到文化广场,在文化广场停留 6 min 后,再匀速步行了 20 min 返回家.
下面图中 x表示时间,y 表示离家的距离.图象反映了这个过程中张华离家的距离与时间
之间的对应关系.
y / km
1.5
0.6
O 4 19 25 31 51 x / min
第(23)题
请根据相关信息,回答下列问题:
(Ⅰ)① 填表:
张华离开家的时间∕min 1 4 13 30
张华离家的距离∕km 0.6
② 填空:张华从文化广场返回家的速度为 km / min ;
③ 当0≤x≤25时,请直接写出张华离家的距离 y 关于时间 x 的函数解析式;
(Ⅱ)当张华离开家8 min 时,他的爸爸也从家出发匀速步行了 20 min 直接到达了
文化广场,那么从画社到文化广场的途中(0.6<y<1.5)两人相遇时离家的距离是多少?
(直接写出结果即可)
数学试卷 第 7 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(24)(本小题 10 分)
将一个平行四边形纸片OABC 放置在平面直角坐标系中,点O(0,0),点 A(3,0),
点 B ,C 在第一象限,且OC 2 , AOC 60 .
(Ⅰ)填空:如图①,点C 的坐标为 ,点 B 的坐标为 ;
(Ⅱ)若 P 为 x轴的正半轴上一动点,过点 P 作直线 l x轴,沿直线 l 折叠该纸片,
折叠后点O 的对应点O 落在 x轴的正半轴上,点C 的对应点为C .设OP t .
① 如图②,若直线 l 与边CB 相交于点Q,当折叠后四边形PO C Q 与 OABC 重叠
部分为五边形时,O C 与 AB 相交于点 E .试用含有 t 的式子表示线段 BE 的长,并直接
写出 t 的取值范围;
2 11
② 设折叠后重叠部分的面积为 S ,当 ≤ t ≤ 时,求 S 的取值范围(直接写出
3 4
结果即可).
y y
l
C B C Q C B
E
O A x O P A O x
图① 图②
第(24)题
(25)(本小题 10 分)
已知抛物线 y ax2 bx c ( a ,b ,c 为常数,a 0)的顶点为 P ,且 2a b 0,
对称轴与 x轴相交于点 D ,点M(m,1)在抛物线上,m 1,O 为坐标原点.
(Ⅰ)当 a 1, c 1时,求该抛物线顶点 P 的坐标;
13
(Ⅱ)当OM OP 时,求 a的值;
2
(Ⅲ)若 N 是抛物线上的点,且点N 在第四象限, MDN 90 ,DM DN ,点E 在
线段MN 上,点F 在线段DN 上,NE NF 2DM ,当DE MF 取得最小值为 15 时,
求a的值.
数学试卷 第 8 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
机密★启用前
2024 年天津市初中学业水平考试
数学参考答案
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)
(1)D (2)B (3)C (4)C (5)C (6)A
(7)A (8)B (9)A (10)B (11)D (12)C
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
3
(13) (14) x2 (15)10
10
10
(16)1(答案不唯一,满足 k 0 即可) (17)(Ⅰ) 2 ; (Ⅱ)
2
(18)(Ⅰ) 2 ; (Ⅱ)如图,根据题意,切点为 M ;
M1 D A
连接 ME 并延长,与网格线相交于点 M1 ;取圆与网格 N G
H
线的交点 D 和格点H ,连接DH 并延长,与网格线相交 E
P
B
于点M 2 ;连接M1M 2 ,分别与AB ,AC 相交于点N ,P , F
M C M2
则点M , N , P 即为所求.
三、解答题(本大题共 7 小题,共 66 分)
(19)(本小题 8 分)
解:(Ⅰ) x≤1;
(Ⅱ) x≥ 3;
(Ⅲ)
4 3 2 1 0 1 2
(Ⅳ) 3≤ x≤1.
(20)(本小题 8 分)
解:(Ⅰ)50 , 34 ,8,8.
(Ⅱ)观察条形统计图,
6 3 7 7 8 17 9 15 10 8
∵ x 8.36 ,
3 7 17 15 8
∴ 这组数据的平均数是8.36 .
数学参考答案 第 1 页(共 5 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(Ⅲ)∵ 在所抽取的样本中,每周参加科学教育的时间是 9 h 的学生占30% ,
∴ 根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是9 h
的学生占30% ,有500 30% 150.
∴ 估计该校八年级学生每周参加科学教育的时间是 9 h 的人数约为150 .
(21)(本小题 10 分)
解:(Ⅰ)∵ AB 为⊙O 的弦, E
∴ OA OB .得 A ABO . A D B
∵ △AOB 中, A ABO AOB 180 , O
又 ABO 30 ,
M C N
∴ AOB 180 2 ABO 120 .
∵ 直线MN 与⊙O 相切于点C ,CE 为⊙O 的直径,
∴ CE MN .即 ECM 90 .又 AB // MN ,
∴ CDB ECM 90 .
在 Rt△ODB中, BOE 90 ABO 60 .
1
∵ BCE BOE ,
2
∴ BCE 30 .
(Ⅱ)如图,连接OC . A
同(Ⅰ),得 COB 90 . G
O B
∵ CG AB ,得 FGB 90 . F
∴ 在Rt△FGB 中,由 ABO 30 ,
M C N
得 BFG 90 ABO 60 .
∴ CFO BFG 60 .
OC
在Rt△COF 中, tan CFO ,OC OA 3,
OF
OC 3
∴ OF 3 .
tan CFO tan 60
数学参考答案 第 2 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(22)(本小题 10 分)
解:(Ⅰ)设CD x ,由DE 36,得CE CD DE x 36.
∵ EC AB ,垂足为C ,
∴ BCE ACD 90 .
BC
在 Rt△BCD 中, tan CDB , CDB 45 ,
CD
∴ BC CD tan CDB x tan 45 x .
BC
在 Rt△BCE 中, tan CEB , CEB 31 ,
CE
∴ BC CE tan CEB (x 36) tan 31 .
36 tan 31 36 0.6
∴ x (x 36) tan 31 .得 x 54.
1 tan 31 1 0.6
答:线段CD 的长约为54 m.
AC
(Ⅱ)在Rt△ACD 中, tan CDA , CDA 6 ,
CD
∴ AC CD tan CDA 54 tan 6 54 0.1 5.4 .
∴ AB AC BC 5.4 54 59 .
答:桥塔 AB 的高度约为59 m.
(23)(本小题 10 分)
解:(Ⅰ)① 0.15 , 0.6 ,1.5 ;
② 0.075;
③ 当0≤x≤4时, y 0.15x ;
当 4<x≤19 时, y 0.6;
当19<x≤25时, y 0.15x 2.25.
(Ⅱ)1.05 km.
(24)(本小题 10 分)
解:(Ⅰ)(1, 3),(4, 3).
(Ⅱ)① 由折叠知, OO C AOC 60 ,O P OP t ,则OO 2t .
∵ 点 A(3,0),得OA 3.
∴ AO OO OA 2t 3.
数学参考答案 第 3 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
∵ 四边形OABC 为平行四边形,
∴ AB OC 2 , AB // OC .得 O AB AOC 60 .
∴ △AO E 为等边三角形.有 AE AO 2t 3.
∵ BE AB AE ,即 BE 2 (2t 3) 5 2t ,
3 5
∴ BE 2t 5,其中 t 的取值范围是 <t< .
2 2
2 3 5 3
② ≤S≤ .
9 4
(25)(本小题 10 分)
解:(Ⅰ)∵ 2a b 0, a 1,得b 2a 2 .又 c 1,
∴ 该抛物线的解析式为 y x2 2x 1.
∵ y x2 2x 1 (x 1
2
) 2 ,
∴ 该抛物线顶点 P 的坐标为(1, 2).
(Ⅱ)过点 M(m,1)作MH x 轴,垂足为H ,m 1,
则 MHO 90 ,HM 1,OH m .
13
在 Rt△MOH 中,由HM 2 OH 2 OM 2 ,OM ,
2
2 13 3 3∴ 1 m ( )2.解得m ,1 m2 (舍).
2 2 2
3
∴ 点M 的坐标为( ,1).
2
b
∵ 2a b 0,即 1.
2a
∴ 抛物线 y ax2 2ax c 的对称轴为 x 1.
∵ 对称轴与 x轴相交于点D ,则OD 1, ODP 90 .
2 2 2 13在 Rt△OPD中,由OD PD OP ,OP ,
2
∴ 1 PD2
13 2 3 ( ).解得 PD .
2 2
3
由 a 0 ,得该抛物线顶点P 的坐标为(1, ).
2
3
∴ 该抛物线的解析式为 y a(x 1)2 .
2
数学参考答案 第 4 页(共 5 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
3 3 3
∵ 点M( ,1)在该抛物线上,有1 a( 1)
2 .
2 2 2
∴ a 10.
(Ⅲ)过点 M(m,1)作MH x 轴,垂足为H ,m 1,
则 MHO 90 ,HM 1,OH m .
∴ DH OH OD m 1.
∴ 在 2 2 2 2Rt△DMH 中,DM DH HM (m 1) 1.
过点 N 作 NK x轴,垂足为K ,则 DKN 90 .
∵ MDN 90 , DM DN ,又 DNK 90 NDK MDH ,
∴ △NDK ≌△DMH .得点 N 的坐标为(2,1 m).
在 Rt△DMN 中, DMN DNM 45 ,
MN 2 DM 2 DN 2 2DM 2 ,即MN 2DM .
根据题意, NE NF 2DM ,得ME NF .
在△DMN 的外部,作 DNG 45 ,且 NG DM ,连接GF ,
得 MNG= DNM + DNG 90 .
∴ △GNF ≌△DME .有GF DE .
∴ DE MF GF MF ≥GM .
当满足条件的点 F 落在线段GM 上时,DE MF 取得最小值,即GM 15 .
在 2 2Rt△GMN 中,GM NG MN 2 3DM 2 ,
∴ ( 15)2 3DM 2 .得DM 2 5.
∴ (m 1)2 1 5 .解得m1 3,m2 1(舍).
∴ 点M 的坐标为(3,1),点 N 的坐标为(2, 2).
∵ 2 点M(3,1), N(2, 2)都在抛物线 y ax 2ax c上,
得1 9a 6a c , 2 4a 4a c .
∴ a 1.
数学参考答案 第 5 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
2024 年天津市初中学业水平考试试卷
数 学
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷为第 1 页至第 3
页,第Ⅱ卷为第 4 页至第 8 页。试卷满分 120 分。考试时间 100 分钟。
答卷前,请务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”
上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案
答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。
祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用 2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共 12 题,共 36 分。
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分. 在每小题给出的四个选项中,
只有一项是符合题目要求的)
(1)计算3 ( 3)的结果等于
(A) 6 (B) 0
(C)3 (D) 6
(2)右图是一个由5个相同的正方体组成的立体图形,它的主视图是
(A) (B)
第(2)题
(C) (D)
数学试卷 第 1 页(共 8 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(3)估计 10 的值在
(A)1和 2 之间 (B) 2 和3之间
(C)3和 4 之间 (D) 4 和 5 之间
(4)在一些美术字中,有的汉字是轴对称图形.下面 4 个汉字中,可以看作是轴对称
图形的是
(A) (B) (C) (D)
(5)据 2024 年 4 月 18 日《天津日报》报道,天津市组织开展了第 43 届“爱鸟周”
大型主题宣传活动.据统计,今春过境我市候鸟总数已超过 800 000 只.将数据
800 000 用科学记数法表示应为
(A)0.08 107 (B)0.8 106
(C)8 105 (D)80 104
(6) 2 cos45 1的值等于
(A) 0 (B)1
2
(C) 1 (D) 2 1
2
3x 3
(7)计算 的结果等于
x 1 x 1
(A)3 (B) x
x 3
(C) (D)
x 1 x2 1
5
(8)若点 A(x , 1),B(x2 ,11 ),C(x3 ,5)都在反比例函数 y 的图象上,则 x1 , x2 ,
x
x3 的大小关系是
(A) x1 x2 x3 (B) x1 x3 x2
(C) x3 x2 x1 (D) x2 x1 x3
数学试卷 第 2 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(9)《孙子算经》是我国古代著名的数学典籍,其中有一道题:“今有木,不知长短.引
绳度之,余绳四尺五寸;屈绳度之,不足一尺.木长几何?”意思是:用一根绳子
去量一根长木,绳子还剩余 4.5 尺;将绳子对折再量长木,长木还剩余1尺.问木长
多少尺?设木长 x尺,绳子长 y 尺,则可以列出的方程组为
y x 4.5, y x 4.5,
(A) (B)
x 0.5y 1 x 0.5y 1
x y 4.5, x y 4.5,
(C) (D)
x y 1 y x 1
(10)如图, Rt△ABC 中, C 90 , B 40 ,以点 A 为圆心,适当长为半径画弧,
1
交 AB 于点 E ,交 AC 于点 F ;再分别以点 E , F 为圆心,大于 EF 的长为半径
2
画弧,两弧(所在圆的半径相等)在 BAC 的内部相交于点 P ;画射线 AP ,与 BC
C
P
相交于点 D ,则 ADC 的大小为 D
F
(A)60 (B)65
A E B
(C)70 (D)75 第(10)题
(11)如图,△ABC 中, B 30 ,将△ABC 绕点C 顺时针旋转
E
60 得到△DEC ,点 A , B 的对应点分别为 D , E ,延长 F
D
BA 交 DE 于点 F ,下列结论一定正确的是 A
(A) ACB ACD (B) AC // DE
B C
(C) AB EF (D) BF CE 第(11)题
(12)从地面竖直向上抛出一小球,小球的高度 h (单位: m)与小球的运动时间 t
(单位: s )之间的关系式是 h 30t 5t2 (0≤ t≤6).有下列结论:
① 小球从抛出到落地需要6 s ;
② 小球运动中的高度可以是 30 m ;
③ 小球运动 2 s时的高度小于运动5 s时的高度.
其中,正确结论的个数是
(A) 0 (B)1
(C) 2 (D)3
数学试卷 第 3 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
机密★启用前
2024 年天津市初中学业水平考试试卷
数 学
第Ⅱ卷
注意事项:
1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用 2B 铅笔)。
2.本卷共 13 题,共 84 分。
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
(13)不透明袋子中装有10 个球,其中有3个绿球、4 个黑球、3个红球,这些球除颜色
外无其他差别.从袋子中随机取出1个球,则它是绿球的概率为 .
(14)计算 x8 x6 的结果为 .
(15)计算( 11 1)( 11 1)的结果为 .
(16)若正比例函数 y kx ( k 是常数, k 0)的图象经过第三、第一象限,则 k 的值
可以是 (写出一.个.即可).
E
F
(17)如图,正方形 ABCD 的边长为 D3 2 ,对角线 AC , BD相交 A
于点O ,点 E 在CA 的延长线上,OE 5,连接 DE .
O
(Ⅰ)线段 AE 的长为 ;
B C
(Ⅱ)若 F 为 DE 的中点,则线段 AF 的长为 . 第(17)题
(18)如图,在每个小正方形的边长为1的网格中,点 A , F ,G 均在格点上.
(Ⅰ)线段 AG 的长为 ; A
(Ⅱ)点 E 在水平网格线上,过点 A , E , F 作圆,
G
经过圆与水平网格线的交点作切线,分别与 AE ,AF E
B
的延长线相交于点 B ,C .△ABC 中,点M 在边 BC F
C
上,点 N 在边 AB 上,点 P 在边 AC 上.请用无.刻.度. 第(18)题
的直尺,在如图所示的网格中,画出点 M , N , P ,使△MNP 的周长最短,并
简要说明点M , N , P 的位置是如何找到的(不要求证明) .
数学试卷 第 4 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
三、解答题(本大题共 7 小题,共 66 分.解答应写出文字说明、演算步骤或推理过程)
(19)(本小题 8 分)
2x 1≤3, ①
解不等式组
3x 1≥ x 7. ②
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
4 3 2 1 0 1 2
(Ⅳ)原不等式组的解集为 .
(20)(本小题 8 分)
为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级
a名学生,根据统计的结果,绘制出如下的统计图①和图②.
人数
6 h 18 17
10 h 6% 16 15
7 h
16% 14
14%
12
10
8
9 h 8 7
30% 8 h 6
m% 4 3
2
0
6 7 8 9 10 时间/ h
图① 图②
第(20)题
请根据相关信息,解答下列问题:
(Ⅰ)填空: a的值为 ,图①中 m 的值为 ,统计的这组学生
每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(Ⅱ)求统计的这组学生每周参加科学教育的时间数据的平均数;
(Ⅲ)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加
科学教育的时间是 9 h 的人数约为多少?
数学试卷 第 5 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(21)(本小题 10 分)
已知△AOB 中, ABO 30 , AB 为⊙O 的弦,直线 MN 与⊙O 相切于点C .
(Ⅰ)如图①,若 AB // MN ,直径CE 与 AB 相交于点D ,求 AOB 和 BCE 的大小;
(Ⅱ)如图②,若OB // MN ,CG AB ,垂足为G ,CG 与OB 相交于点 F ,OA 3,
求线段OF 的长.
E
A
A D B
G
O O BF
M C N M C N
图① 图②
第(21)题
(22)(本小题 10 分)
综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔 AB 的高度(如图①).
某学习小组设计了一个方案:如图②,点C , D , E 依次在同一条水平直线上,
DE 36 m , EC AB ,垂足为C .在 D 处测得桥塔顶部 B 的仰角( CDB )为 45 ,
测得桥塔底部 A的俯角( CDA)为6 ,又在E 处测得桥塔顶部B 的仰角( CEB )为31 .
(Ⅰ)求线段CD 的长(结果取整数);
(Ⅱ)求桥塔 AB 的高度(结果取整数).
参考数据: tan 31 0.6, tan 6 0.1.
B B
C E
A A D
图① 图②
第(22)题
数学试卷 第 6 页(共 8 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(23)(本小题 10 分)
已知张华的家、画社、文化广场依次在同一条直线上,画社离家 0.6 km ,文化广场
离家1.5 km .张华从家出发,先匀速骑行了 4 min 到画社,在画社停留了15 min ,之后
匀速骑行了 6 min 到文化广场,在文化广场停留 6 min 后,再匀速步行了 20 min 返回家.
下面图中 x表示时间,y 表示离家的距离.图象反映了这个过程中张华离家的距离与时间
之间的对应关系.
y / km
1.5
0.6
O 4 19 25 31 51 x / min
第(23)题
请根据相关信息,回答下列问题:
(Ⅰ)① 填表:
张华离开家的时间∕min 1 4 13 30
张华离家的距离∕km 0.6
② 填空:张华从文化广场返回家的速度为 km / min ;
③ 当0≤x≤25时,请直接写出张华离家的距离 y 关于时间 x 的函数解析式;
(Ⅱ)当张华离开家8 min 时,他的爸爸也从家出发匀速步行了 20 min 直接到达了
文化广场,那么从画社到文化广场的途中(0.6<y<1.5)两人相遇时离家的距离是多少?
(直接写出结果即可)
数学试卷 第 7 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(24)(本小题 10 分)
将一个平行四边形纸片OABC 放置在平面直角坐标系中,点O(0,0),点 A(3,0),
点 B ,C 在第一象限,且OC 2 , AOC 60 .
(Ⅰ)填空:如图①,点C 的坐标为 ,点 B 的坐标为 ;
(Ⅱ)若 P 为 x轴的正半轴上一动点,过点 P 作直线 l x轴,沿直线 l 折叠该纸片,
折叠后点O 的对应点O 落在 x轴的正半轴上,点C 的对应点为C .设OP t .
① 如图②,若直线 l 与边CB 相交于点Q,当折叠后四边形PO C Q 与 OABC 重叠
部分为五边形时,O C 与 AB 相交于点 E .试用含有 t 的式子表示线段 BE 的长,并直接
写出 t 的取值范围;
2 11
② 设折叠后重叠部分的面积为 S ,当 ≤ t ≤ 时,求 S 的取值范围(直接写出
3 4
结果即可).
y y
l
C B C Q C B
E
O A x O P A O x
图① 图②
第(24)题
(25)(本小题 10 分)
已知抛物线 y ax2 bx c ( a ,b ,c 为常数,a 0)的顶点为 P ,且 2a b 0,
对称轴与 x轴相交于点 D ,点M(m,1)在抛物线上,m 1,O 为坐标原点.
(Ⅰ)当 a 1, c 1时,求该抛物线顶点 P 的坐标;
13
(Ⅱ)当OM OP 时,求 a的值;
2
(Ⅲ)若 N 是抛物线上的点,且点N 在第四象限, MDN 90 ,DM DN ,点E 在
线段MN 上,点F 在线段DN 上,NE NF 2DM ,当DE MF 取得最小值为 15 时,
求a的值.
数学试卷 第 8 页(共 8 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
机密★启用前
2024 年天津市初中学业水平考试
数学参考答案
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)
(1)D (2)B (3)C (4)C (5)C (6)A
(7)A (8)B (9)A (10)B (11)D (12)C
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
3
(13) (14) x2 (15)10
10
10
(16)1(答案不唯一,满足 k 0 即可) (17)(Ⅰ) 2 ; (Ⅱ)
2
(18)(Ⅰ) 2 ; (Ⅱ)如图,根据题意,切点为 M ;
M1 D A
连接 ME 并延长,与网格线相交于点 M1 ;取圆与网格 N G
H
线的交点 D 和格点H ,连接DH 并延长,与网格线相交 E
P
B
于点M 2 ;连接M1M 2 ,分别与AB ,AC 相交于点N ,P , F
M C M2
则点M , N , P 即为所求.
三、解答题(本大题共 7 小题,共 66 分)
(19)(本小题 8 分)
解:(Ⅰ) x≤1;
(Ⅱ) x≥ 3;
(Ⅲ)
4 3 2 1 0 1 2
(Ⅳ) 3≤ x≤1.
(20)(本小题 8 分)
解:(Ⅰ)50 , 34 ,8,8.
(Ⅱ)观察条形统计图,
6 3 7 7 8 17 9 15 10 8
∵ x 8.36 ,
3 7 17 15 8
∴ 这组数据的平均数是8.36 .
数学参考答案 第 1 页(共 5 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(Ⅲ)∵ 在所抽取的样本中,每周参加科学教育的时间是 9 h 的学生占30% ,
∴ 根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是9 h
的学生占30% ,有500 30% 150.
∴ 估计该校八年级学生每周参加科学教育的时间是 9 h 的人数约为150 .
(21)(本小题 10 分)
解:(Ⅰ)∵ AB 为⊙O 的弦, E
∴ OA OB .得 A ABO . A D B
∵ △AOB 中, A ABO AOB 180 , O
又 ABO 30 ,
M C N
∴ AOB 180 2 ABO 120 .
∵ 直线MN 与⊙O 相切于点C ,CE 为⊙O 的直径,
∴ CE MN .即 ECM 90 .又 AB // MN ,
∴ CDB ECM 90 .
在 Rt△ODB中, BOE 90 ABO 60 .
1
∵ BCE BOE ,
2
∴ BCE 30 .
(Ⅱ)如图,连接OC . A
同(Ⅰ),得 COB 90 . G
O B
∵ CG AB ,得 FGB 90 . F
∴ 在Rt△FGB 中,由 ABO 30 ,
M C N
得 BFG 90 ABO 60 .
∴ CFO BFG 60 .
OC
在Rt△COF 中, tan CFO ,OC OA 3,
OF
OC 3
∴ OF 3 .
tan CFO tan 60
数学参考答案 第 2 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
(22)(本小题 10 分)
解:(Ⅰ)设CD x ,由DE 36,得CE CD DE x 36.
∵ EC AB ,垂足为C ,
∴ BCE ACD 90 .
BC
在 Rt△BCD 中, tan CDB , CDB 45 ,
CD
∴ BC CD tan CDB x tan 45 x .
BC
在 Rt△BCE 中, tan CEB , CEB 31 ,
CE
∴ BC CE tan CEB (x 36) tan 31 .
36 tan 31 36 0.6
∴ x (x 36) tan 31 .得 x 54.
1 tan 31 1 0.6
答:线段CD 的长约为54 m.
AC
(Ⅱ)在Rt△ACD 中, tan CDA , CDA 6 ,
CD
∴ AC CD tan CDA 54 tan 6 54 0.1 5.4 .
∴ AB AC BC 5.4 54 59 .
答:桥塔 AB 的高度约为59 m.
(23)(本小题 10 分)
解:(Ⅰ)① 0.15 , 0.6 ,1.5 ;
② 0.075;
③ 当0≤x≤4时, y 0.15x ;
当 4<x≤19 时, y 0.6;
当19<x≤25时, y 0.15x 2.25.
(Ⅱ)1.05 km.
(24)(本小题 10 分)
解:(Ⅰ)(1, 3),(4, 3).
(Ⅱ)① 由折叠知, OO C AOC 60 ,O P OP t ,则OO 2t .
∵ 点 A(3,0),得OA 3.
∴ AO OO OA 2t 3.
数学参考答案 第 3 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
∵ 四边形OABC 为平行四边形,
∴ AB OC 2 , AB // OC .得 O AB AOC 60 .
∴ △AO E 为等边三角形.有 AE AO 2t 3.
∵ BE AB AE ,即 BE 2 (2t 3) 5 2t ,
3 5
∴ BE 2t 5,其中 t 的取值范围是 <t< .
2 2
2 3 5 3
② ≤S≤ .
9 4
(25)(本小题 10 分)
解:(Ⅰ)∵ 2a b 0, a 1,得b 2a 2 .又 c 1,
∴ 该抛物线的解析式为 y x2 2x 1.
∵ y x2 2x 1 (x 1
2
) 2 ,
∴ 该抛物线顶点 P 的坐标为(1, 2).
(Ⅱ)过点 M(m,1)作MH x 轴,垂足为H ,m 1,
则 MHO 90 ,HM 1,OH m .
13
在 Rt△MOH 中,由HM 2 OH 2 OM 2 ,OM ,
2
2 13 3 3∴ 1 m ( )2.解得m ,1 m2 (舍).
2 2 2
3
∴ 点M 的坐标为( ,1).
2
b
∵ 2a b 0,即 1.
2a
∴ 抛物线 y ax2 2ax c 的对称轴为 x 1.
∵ 对称轴与 x轴相交于点D ,则OD 1, ODP 90 .
2 2 2 13在 Rt△OPD中,由OD PD OP ,OP ,
2
∴ 1 PD2
13 2 3 ( ).解得 PD .
2 2
3
由 a 0 ,得该抛物线顶点P 的坐标为(1, ).
2
3
∴ 该抛物线的解析式为 y a(x 1)2 .
2
数学参考答案 第 4 页(共 5 页)
{#{QQABKIQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
3 3 3
∵ 点M( ,1)在该抛物线上,有1 a( 1)
2 .
2 2 2
∴ a 10.
(Ⅲ)过点 M(m,1)作MH x 轴,垂足为H ,m 1,
则 MHO 90 ,HM 1,OH m .
∴ DH OH OD m 1.
∴ 在 2 2 2 2Rt△DMH 中,DM DH HM (m 1) 1.
过点 N 作 NK x轴,垂足为K ,则 DKN 90 .
∵ MDN 90 , DM DN ,又 DNK 90 NDK MDH ,
∴ △NDK ≌△DMH .得点 N 的坐标为(2,1 m).
在 Rt△DMN 中, DMN DNM 45 ,
MN 2 DM 2 DN 2 2DM 2 ,即MN 2DM .
根据题意, NE NF 2DM ,得ME NF .
在△DMN 的外部,作 DNG 45 ,且 NG DM ,连接GF ,
得 MNG= DNM + DNG 90 .
∴ △GNF ≌△DME .有GF DE .
∴ DE MF GF MF ≥GM .
当满足条件的点 F 落在线段GM 上时,DE MF 取得最小值,即GM 15 .
在 2 2Rt△GMN 中,GM NG MN 2 3DM 2 ,
∴ ( 15)2 3DM 2 .得DM 2 5.
∴ (m 1)2 1 5 .解得m1 3,m2 1(舍).
∴ 点M 的坐标为(3,1),点 N 的坐标为(2, 2).
∵ 2 点M(3,1), N(2, 2)都在抛物线 y ax 2ax c上,
得1 9a 6a c , 2 4a 4a c .
∴ a 1.
数学参考答案 第 5 页(共 5 页)
{#{QQABIKQQYaAtxggiiQgAgoTBACACQ4hKCQwWHSCCAMo QkkIACEjJCWAgasgxOVBAFAAOAAMwAKAQAZgNQANBAKBAC=A}#=}}#}
同课章节目录
