2023-2024学年广东省东莞市三校高一下学期期中联考数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省东莞市三校高一下学期期中联考数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 522.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 00:00:00 | ||
图片预览




文档简介
2023-2024学年广东省东莞市三校高一下学期期中联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知按从小到大顺序排列的两组数据:甲组:,,,,,;乙组:,,,,,若这两组数据的第百分位数对应相等,第百分位数也对应相等,则( )
A. B. C. D.
3.某大学共有教师人,其中教授、副教授、讲师、助教的人数比为,现用分层抽样的方法从全校所有教师中抽取一个容量为的样本,如果样本按比例分配,那么讲师应抽取的人数为( )
A. B. C. D.
4.已知平面向量,的夹角为,且,,则在方向上的投影向量为( )
A. B. C. D.
5.已知某地区中小学共有学生人,各学段学生所占比例如图甲所示,近视情况如图乙所示,则该地区初中生近视的人数为( )
A. B. C. D.
6.由斜二测画法得到的一个水平放置的三角形的直观图是等腰三角形,底角为,腰长为,如图,那么它在原平面图形中,顶点到轴的距离是( )
A. B. C. D.
7.记的内角的对边分别为,设向量若,则( )
A. B. C. D.
8.数学汇编第卷中记载着一个确定重心的定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以该闭合图形的重心旋转所得周长的积”,即表示平面图形绕旋转轴旋转的体积,表示平面图形的面积,表示重心绕旋转轴旋转一周的周长如图,等腰梯形,已知,则其重心到的距离为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设是复数,则下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.在中,内角,,的对边分别为,,,下列命题中正确的是( )
A. 若,则
B. 若为锐角三角形,则
C. 若,则一定是等腰直角三角形
D. 若,,则一定是等边三角形
11.已知正方体的棱长为分别为的中点下列说法正确的是( )
A. 点到平面的距离为
B. 正方体外接球的体积为
C. 面截正方体外接球所得圆的面积为
D. 以顶点为球心,为半径作一个球,则球面与正方体的表面相交所得到的曲线的长等于
三、填空题:本题共3小题,每小题5分,共15分。
12.写出一个同时满足的复数 ;.
13.已知正四棱台的上下底边长分别为,正四棱台体积为,则此表面积为
14.窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一,每年新春佳节,我国许多地区的人们都有贴窗花的习俗,以此达到装点环境、渲染气氛的目的,并寄托着辞旧迎新、接福纳祥的愿望图是一张由卷曲纹和回纹构成的正六边形剪纸窗花,已知图中正六边形的边长为,圆的圆心为正六边形的中心,半径为,若点在正六边形的边上运动,为圆的直径,则的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
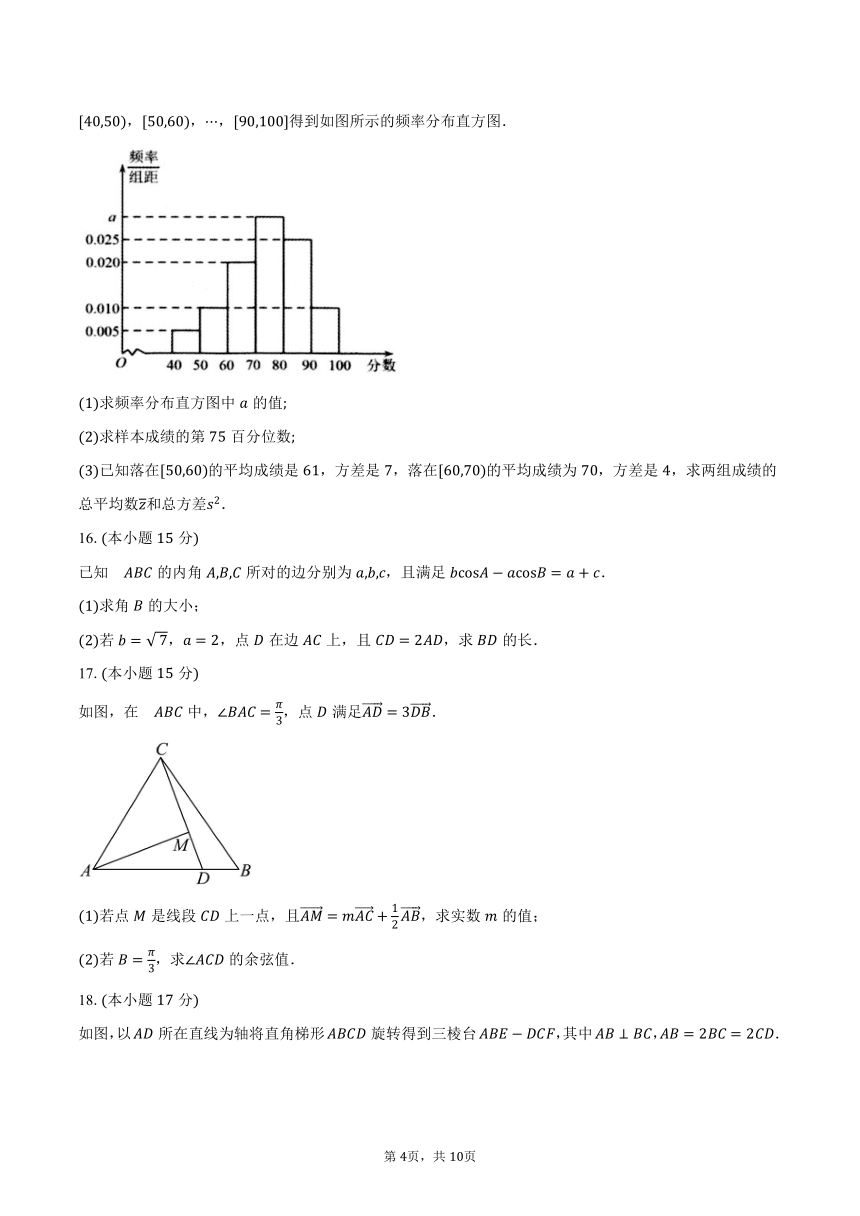
文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均为不低于分的整数分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值
求样本成绩的第百分位数
已知落在的平均成绩是,方差是,落在的平均成绩为,方差是,求两组成绩的总平均数和总方差.
16.本小题分
已知的内角所对的边分别为,且满足.
求角的大小;
若,,点在边上,且,求的长.
17.本小题分
如图,在中,,点满足.
若点是线段上一点,且,求实数的值;
若,求的余弦值.
18.本小题分
如图,以所在直线为轴将直角梯形旋转得到三棱台,其中,.
求证:;
若,求直线与平面所成角的正弦值.
19.本小题分
由于年月份国内疫情爆发,经济活动大范围停顿,餐饮业受到重大影响月份复工复产工作逐步推进,居民生活逐步恢复正常李克强总理在月日考察山东烟台一处老旧小区时提到,地摊经济小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机某商场经营者陈某准备在商场门前“摆地摊”,经营冷饮生意已知该商场门前是一块角形区域,如图所示,其中,且在该区域内点处有一个路灯,经测量点到区域边界、的距离分别为,,为长度单位陈某准备过点修建一条长椅点,分别落在、上,长椅的宽度及路灯的粗细忽略不计,以供购买冷饮的人休息.
求点到点的距离;
为优化经营面积,当等于多少时,该三角形区域面积最小?并求出面积的最小值.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12.. 或 写一个即可
13..
14..
15..解:每组小矩形的面积之和为,
,
;
成绩落在内的频率为,
落在内的频率为,
设第百分位数为,
由,
得,故第百分位数为;
由图可知,成绩在的市民人数为,
成绩在的市民人数为,
故,
设成绩在中人的分数分别为,,,,
成绩在中人的分数分别为,,,,,
则由题意可得,,,
即,,
,
所以两组市民成绩的总平均数是,总方差是.
16..解:
因为,
由余弦定理得,
整理可得,
所以,又,
所以.
因为
所以由正弦定理可得,
由,可得为锐角,可得,
由余弦定理得故
整理可得解得或舍去,
又点在边上,且所以
所以在中,由余弦定理可得.
17..解:设,,
因为,所以,
,
又,
所以,所以,所以实数的值为;
因为,所以,
由题意设,所以,
在中,,
在中,,
由可得,
所以,
所以,又,,所以,
所以的余弦值为.
18..解:连接,,设,则,
取的中点,连接,则四边形为正方形,故,
得,,
同理可得,,又面,
面,又面,;
由知,
又,,
由,得.
又,面,面,
过点作交于点,连接.
因为面,所以,又因为,且面,
则面,又面,面面.
过点作交于点,连接.
就是直线与面所成的线面角.
面面,就是直线与面所成的线面角.
,又,,,
又,,
即直线与平面所成线面角的正弦值为.
19..解:连接,在中,因为,,,
所以,由余弦定理得,,
所以,即点到点的距离为.
由,
,
,
化简得,当且仅当
即时取等号,,
故当时,三角形面积最小,最小值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数满足,则复数在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知按从小到大顺序排列的两组数据:甲组:,,,,,;乙组:,,,,,若这两组数据的第百分位数对应相等,第百分位数也对应相等,则( )
A. B. C. D.
3.某大学共有教师人,其中教授、副教授、讲师、助教的人数比为,现用分层抽样的方法从全校所有教师中抽取一个容量为的样本,如果样本按比例分配,那么讲师应抽取的人数为( )
A. B. C. D.
4.已知平面向量,的夹角为,且,,则在方向上的投影向量为( )
A. B. C. D.
5.已知某地区中小学共有学生人,各学段学生所占比例如图甲所示,近视情况如图乙所示,则该地区初中生近视的人数为( )
A. B. C. D.
6.由斜二测画法得到的一个水平放置的三角形的直观图是等腰三角形,底角为,腰长为,如图,那么它在原平面图形中,顶点到轴的距离是( )
A. B. C. D.
7.记的内角的对边分别为,设向量若,则( )
A. B. C. D.
8.数学汇编第卷中记载着一个确定重心的定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以该闭合图形的重心旋转所得周长的积”,即表示平面图形绕旋转轴旋转的体积,表示平面图形的面积,表示重心绕旋转轴旋转一周的周长如图,等腰梯形,已知,则其重心到的距离为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设是复数,则下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.在中,内角,,的对边分别为,,,下列命题中正确的是( )
A. 若,则
B. 若为锐角三角形,则
C. 若,则一定是等腰直角三角形
D. 若,,则一定是等边三角形
11.已知正方体的棱长为分别为的中点下列说法正确的是( )
A. 点到平面的距离为
B. 正方体外接球的体积为
C. 面截正方体外接球所得圆的面积为
D. 以顶点为球心,为半径作一个球,则球面与正方体的表面相交所得到的曲线的长等于
三、填空题:本题共3小题,每小题5分,共15分。
12.写出一个同时满足的复数 ;.
13.已知正四棱台的上下底边长分别为,正四棱台体积为,则此表面积为
14.窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一,每年新春佳节,我国许多地区的人们都有贴窗花的习俗,以此达到装点环境、渲染气氛的目的,并寄托着辞旧迎新、接福纳祥的愿望图是一张由卷曲纹和回纹构成的正六边形剪纸窗花,已知图中正六边形的边长为,圆的圆心为正六边形的中心,半径为,若点在正六边形的边上运动,为圆的直径,则的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均为不低于分的整数分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值
求样本成绩的第百分位数
已知落在的平均成绩是,方差是,落在的平均成绩为,方差是,求两组成绩的总平均数和总方差.
16.本小题分
已知的内角所对的边分别为,且满足.
求角的大小;
若,,点在边上,且,求的长.
17.本小题分
如图,在中,,点满足.
若点是线段上一点,且,求实数的值;
若,求的余弦值.
18.本小题分
如图,以所在直线为轴将直角梯形旋转得到三棱台,其中,.
求证:;
若,求直线与平面所成角的正弦值.
19.本小题分
由于年月份国内疫情爆发,经济活动大范围停顿,餐饮业受到重大影响月份复工复产工作逐步推进,居民生活逐步恢复正常李克强总理在月日考察山东烟台一处老旧小区时提到,地摊经济小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机某商场经营者陈某准备在商场门前“摆地摊”,经营冷饮生意已知该商场门前是一块角形区域,如图所示,其中,且在该区域内点处有一个路灯,经测量点到区域边界、的距离分别为,,为长度单位陈某准备过点修建一条长椅点,分别落在、上,长椅的宽度及路灯的粗细忽略不计,以供购买冷饮的人休息.
求点到点的距离;
为优化经营面积,当等于多少时,该三角形区域面积最小?并求出面积的最小值.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12.. 或 写一个即可
13..
14..
15..解:每组小矩形的面积之和为,
,
;
成绩落在内的频率为,
落在内的频率为,
设第百分位数为,
由,
得,故第百分位数为;
由图可知,成绩在的市民人数为,
成绩在的市民人数为,
故,
设成绩在中人的分数分别为,,,,
成绩在中人的分数分别为,,,,,
则由题意可得,,,
即,,
,
所以两组市民成绩的总平均数是,总方差是.
16..解:
因为,
由余弦定理得,
整理可得,
所以,又,
所以.
因为
所以由正弦定理可得,
由,可得为锐角,可得,
由余弦定理得故
整理可得解得或舍去,
又点在边上,且所以
所以在中,由余弦定理可得.
17..解:设,,
因为,所以,
,
又,
所以,所以,所以实数的值为;
因为,所以,
由题意设,所以,
在中,,
在中,,
由可得,
所以,
所以,又,,所以,
所以的余弦值为.
18..解:连接,,设,则,
取的中点,连接,则四边形为正方形,故,
得,,
同理可得,,又面,
面,又面,;
由知,
又,,
由,得.
又,面,面,
过点作交于点,连接.
因为面,所以,又因为,且面,
则面,又面,面面.
过点作交于点,连接.
就是直线与面所成的线面角.
面面,就是直线与面所成的线面角.
,又,,,
又,,
即直线与平面所成线面角的正弦值为.
19..解:连接,在中,因为,,,
所以,由余弦定理得,,
所以,即点到点的距离为.
由,
,
,
化简得,当且仅当
即时取等号,,
故当时,三角形面积最小,最小值为.
第1页,共1页
同课章节目录
