2023-2024学年广东省深圳市深圳大学附属中学、龙城高级中学高一下学期5月月考数学试题(含答案)
文档属性
| 名称 | 2023-2024学年广东省深圳市深圳大学附属中学、龙城高级中学高一下学期5月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 480.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 17:25:43 | ||
图片预览



文档简介
2023-2024学年广东省深圳市深圳大学附属中学、龙城高级中学高一下学期5月月考数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数,则的共轭复数( )
A. B. C. D.
2.已知为共线向量,且,则( )
A. B. C. D.
3.将水平放置的用斜二测画法得到的直观图如图所示,已知,,则边的实际长度为( )
A. B. C. D.
4.党的十八大以来,我国把绿色发展理念融入城乡规划建设管理之中,合理布局城市的生产空间、生活空间、生态空间,持续推进城市园林绿化工作.为践行生态文明的理念,某学校全体师生于月日开展植树活动,购买了樟树、银杏、桂花、梧桐四种树苗共计棵,比例如图所示,高一年级师生、高二年级师生、高三年级师生参加植树活动的人数之比为,若每种树苗均按各年级师生参加植树人数的比例进行分配,则高二年级师生应分得桂花树苗的数量为( )
A. 棵 B. 棵 C. 棵 D. 棵
5.已知非零向量满足,且向量在向量上的投影向量为,则与的夹角为( )
A. B. C. D.
6.在中,已知,,则“”是“”成立的 条件
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
7.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围如图,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分除去两个球缺如图,“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高已知球缺的体积公式为,其中是球的半径,是球缺的高已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为 取
A. B. C. D.
8.在中,是边上一定点,满足,且对于边上任一点,恒有,则为( )
A. 等腰三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知复数,下列结论正确的有( )
A. 若,则
B. 若,则
C. 若复数满足,则在复平面内对应的点的轨迹为圆
D. 若是关于的方程的一个根,则
10.如图,在边长为的正方形中,,分别是,的中点,是的中点,将,分别沿,折起,使,两点重合于,下列说法正确的是( )
A. 若把沿着继续折起,与恰好重合
B.
C. 四面体的外接球体积为
D. 点在面上的射影为的重心
11.如图所示,在边长为的等边三角形中,,且点在以的中点为圆心,为半径的半圆上,若,则( )
A. B. 的最大值为
C. 最大值为 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知样本数据为,,,,,且、是方程的两根,则这组样本数据的方差是 .
13.在正方体的棱长为,为中点,为中点,则异面直线与所成角的余弦值为 .
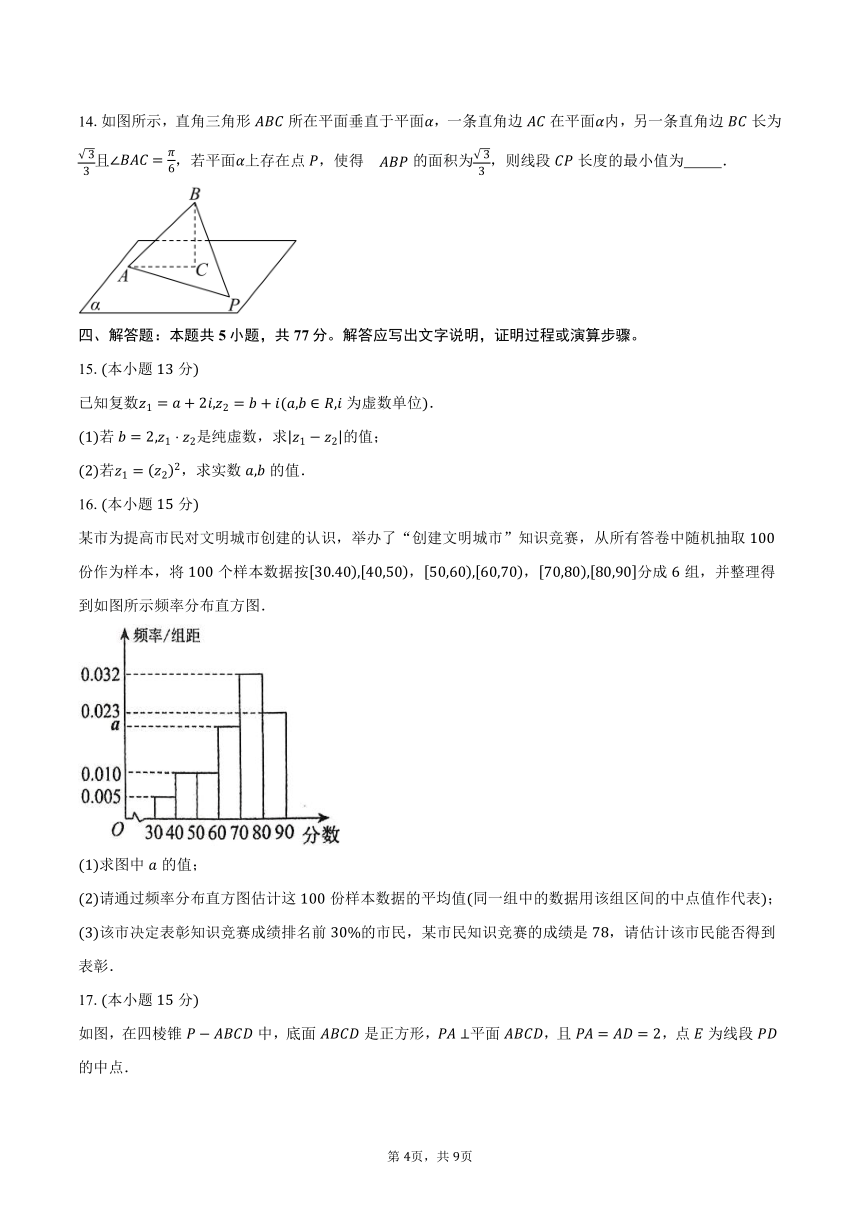
14.如图所示,直角三角形所在平面垂直于平面,一条直角边在平面内,另一条直角边长为且,若平面上存在点,使得的面积为,则线段长度的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知复数为虚数单位.
若是纯虚数,求的值;
若,求实数的值.
16.本小题分
某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将个样本数据按,,分成组,并整理得到如图所示频率分布直方图.
求图中的值;
请通过频率分布直方图估计这份样本数据的平均值同一组中的数据用该组区间的中点值作代表;
该市决定表彰知识竞赛成绩排名前的市民,某市民知识竞赛的成绩是,请估计该市民能否得到表彰.
17.本小题分
如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
求证:平面;
求证:平面;
求三棱锥的体积.
18.本小题分
在中,角,,所对的边分别为,,,且满足.
求角
为边上一点,,且,求C.
19.本小题分
类比于平面三角形中的余弦定理,我们得到三维空间中的三面角余弦定理;如图,由射线、、构成的三面角,,,,二面角的大小为,则.
四棱柱,平面平面,,,求的余弦值;
当、时,证明以上三面角余弦定理;
如图,斜三棱柱中侧面,,的面积分别为,,,各侧面所应得平面与底面所成的三个二面角分别记为,,,请用文字和符号语言描述你能够得到的正弦定理在三维空间中推广的结论,并证明.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12..
13..或
14..或
15..
当时,,
所以,
且是纯虚数,则,解得,
所以,则,
所以.
若,则,
所以,解得.
16..
由频率分布直方图可得,
所以,
份样本数据的平均值为
成绩低于分的频率为,成绩低于分的频率为,
则被表彰的最低成绩为第分位数:因为,
所以估计该市民能得到表彰.
17..
连接交于点,连接,
由底面是正方形,故为中点,
又点为线段的中点,故,
又平面,平面,
故平面;
由点为线段的中点,,故,
由平面,平面,故,
又底面是正方形,故,
又、平面,,
故平面,又平面,
故,又、平面,,
故平面;
由点为线段的中点,故点与点到平面距离相等,
故.
18..解:由,得:,即:,
,即.
又,.
在中,在中,.
又,,代入得:.
根据余弦定理得,所以.
19..
由平面平面,得,
由三面角余弦定理得,
因为,,
所以;
过射线上一点作交于点,
作交于点,连接,如图所示:
则是二面角的平面角,
在中,由余弦定理得:
,
在中,由余弦定理得:
,
两式相减得:
,
则:,
两边同除以,
得;
已知在三棱锥中,,,,
所对的二面角记为,
所对的二面角记为,
对的二面角记为,
求证:.
不难推出,
所以.
作点在底面上的射影,过作于,连接,
过作于,连接,
由,
有,
所以,
因为,,
所以,
同理可得,
所以.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数,则的共轭复数( )
A. B. C. D.
2.已知为共线向量,且,则( )
A. B. C. D.
3.将水平放置的用斜二测画法得到的直观图如图所示,已知,,则边的实际长度为( )
A. B. C. D.
4.党的十八大以来,我国把绿色发展理念融入城乡规划建设管理之中,合理布局城市的生产空间、生活空间、生态空间,持续推进城市园林绿化工作.为践行生态文明的理念,某学校全体师生于月日开展植树活动,购买了樟树、银杏、桂花、梧桐四种树苗共计棵,比例如图所示,高一年级师生、高二年级师生、高三年级师生参加植树活动的人数之比为,若每种树苗均按各年级师生参加植树人数的比例进行分配,则高二年级师生应分得桂花树苗的数量为( )
A. 棵 B. 棵 C. 棵 D. 棵
5.已知非零向量满足,且向量在向量上的投影向量为,则与的夹角为( )
A. B. C. D.
6.在中,已知,,则“”是“”成立的 条件
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
7.灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一种喜庆的氛围如图,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分除去两个球缺如图,“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高已知球缺的体积公式为,其中是球的半径,是球缺的高已知该灯笼的高为,圆柱的高为,圆柱的底面圆直径为,则该灯笼的体积为 取
A. B. C. D.
8.在中,是边上一定点,满足,且对于边上任一点,恒有,则为( )
A. 等腰三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知复数,下列结论正确的有( )
A. 若,则
B. 若,则
C. 若复数满足,则在复平面内对应的点的轨迹为圆
D. 若是关于的方程的一个根,则
10.如图,在边长为的正方形中,,分别是,的中点,是的中点,将,分别沿,折起,使,两点重合于,下列说法正确的是( )
A. 若把沿着继续折起,与恰好重合
B.
C. 四面体的外接球体积为
D. 点在面上的射影为的重心
11.如图所示,在边长为的等边三角形中,,且点在以的中点为圆心,为半径的半圆上,若,则( )
A. B. 的最大值为
C. 最大值为 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知样本数据为,,,,,且、是方程的两根,则这组样本数据的方差是 .
13.在正方体的棱长为,为中点,为中点,则异面直线与所成角的余弦值为 .
14.如图所示,直角三角形所在平面垂直于平面,一条直角边在平面内,另一条直角边长为且,若平面上存在点,使得的面积为,则线段长度的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知复数为虚数单位.
若是纯虚数,求的值;
若,求实数的值.
16.本小题分
某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将个样本数据按,,分成组,并整理得到如图所示频率分布直方图.
求图中的值;
请通过频率分布直方图估计这份样本数据的平均值同一组中的数据用该组区间的中点值作代表;
该市决定表彰知识竞赛成绩排名前的市民,某市民知识竞赛的成绩是,请估计该市民能否得到表彰.
17.本小题分
如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
求证:平面;
求证:平面;
求三棱锥的体积.
18.本小题分
在中,角,,所对的边分别为,,,且满足.
求角
为边上一点,,且,求C.
19.本小题分
类比于平面三角形中的余弦定理,我们得到三维空间中的三面角余弦定理;如图,由射线、、构成的三面角,,,,二面角的大小为,则.
四棱柱,平面平面,,,求的余弦值;
当、时,证明以上三面角余弦定理;
如图,斜三棱柱中侧面,,的面积分别为,,,各侧面所应得平面与底面所成的三个二面角分别记为,,,请用文字和符号语言描述你能够得到的正弦定理在三维空间中推广的结论,并证明.
答案
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
11..
12..
13..或
14..或
15..
当时,,
所以,
且是纯虚数,则,解得,
所以,则,
所以.
若,则,
所以,解得.
16..
由频率分布直方图可得,
所以,
份样本数据的平均值为
成绩低于分的频率为,成绩低于分的频率为,
则被表彰的最低成绩为第分位数:因为,
所以估计该市民能得到表彰.
17..
连接交于点,连接,
由底面是正方形,故为中点,
又点为线段的中点,故,
又平面,平面,
故平面;
由点为线段的中点,,故,
由平面,平面,故,
又底面是正方形,故,
又、平面,,
故平面,又平面,
故,又、平面,,
故平面;
由点为线段的中点,故点与点到平面距离相等,
故.
18..解:由,得:,即:,
,即.
又,.
在中,在中,.
又,,代入得:.
根据余弦定理得,所以.
19..
由平面平面,得,
由三面角余弦定理得,
因为,,
所以;
过射线上一点作交于点,
作交于点,连接,如图所示:
则是二面角的平面角,
在中,由余弦定理得:
,
在中,由余弦定理得:
,
两式相减得:
,
则:,
两边同除以,
得;
已知在三棱锥中,,,,
所对的二面角记为,
所对的二面角记为,
对的二面角记为,
求证:.
不难推出,
所以.
作点在底面上的射影,过作于,连接,
过作于,连接,
由,
有,
所以,
因为,,
所以,
同理可得,
所以.
第1页,共1页
同课章节目录
