桐城中学2008~2009学年度高二第一学期期中考试试题必修三测试题
文档属性
| 名称 | 桐城中学2008~2009学年度高二第一学期期中考试试题必修三测试题 |  | |
| 格式 | rar | ||
| 文件大小 | 61.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-24 23:37:00 | ||
图片预览



文档简介
桐城中学2008~2009学年度第一学期期中考试试题
高二数学试卷
一、选择题:(本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的,将答案的代号填在答案卡上)
1. 有下列四个命题:
①“若x+y =0 ,则x ,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④“不可能事件的概率为0”的逆命题;
其中的真命题为 ( )
A.①② B.②③ C.①③ D.③④
2. 将两个数A=9,B=15交换使得A=15,B=9下列语句正确的一组是( )
A. B. C. D.
3. 在下列各图中,每个图的两个变量具有相关关系的图是
(1) (2) (3) (4)
A.(1)(2) B.(1)(3) C.(2)(4) D.(2)(3)
4. 甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A. B.
C. D.
5. 用秦九韶算法计算多项式在时的值时,的值为 ( )
A. -845 B. 220 C. -57 D. 34
6. 设集合 ,则B是A的子集的一个充分不必要的条件是 ( )
A. B.
C. D.
7.某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车中抽取48辆进行检验,这三种型号的轿车依次应抽取( )
A. 16,16,16 B. 8,30,10 C. 4,33,11 D. 12,27,9
8. 已知命题:,则( )
A. B.
C. D.
9.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是
A. B. C. D.
10. 某初级中学有学生人,其中一年级人,二、三年级各人,现要利用抽样方法取人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为;使用系统抽样时,将学生统一随机编号,并将整个编号依次分为段.如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
11.为配合学校对学生进行交通安全教育,特作如下随机调查:向被调查者提出两个问题:(1)你的学号是偶数吗?(2)你是否闯过红灯?要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)问题,否则回答第(2)问题。被调查者不必告诉调查人自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道回答了哪个问题,所以都如实做了回答。如果随机调查了300人,其中有90人回答了“是”,由此可以估计在这300人中闯过红灯的人数是 ( )
A.15 B.30 C.60 D.75
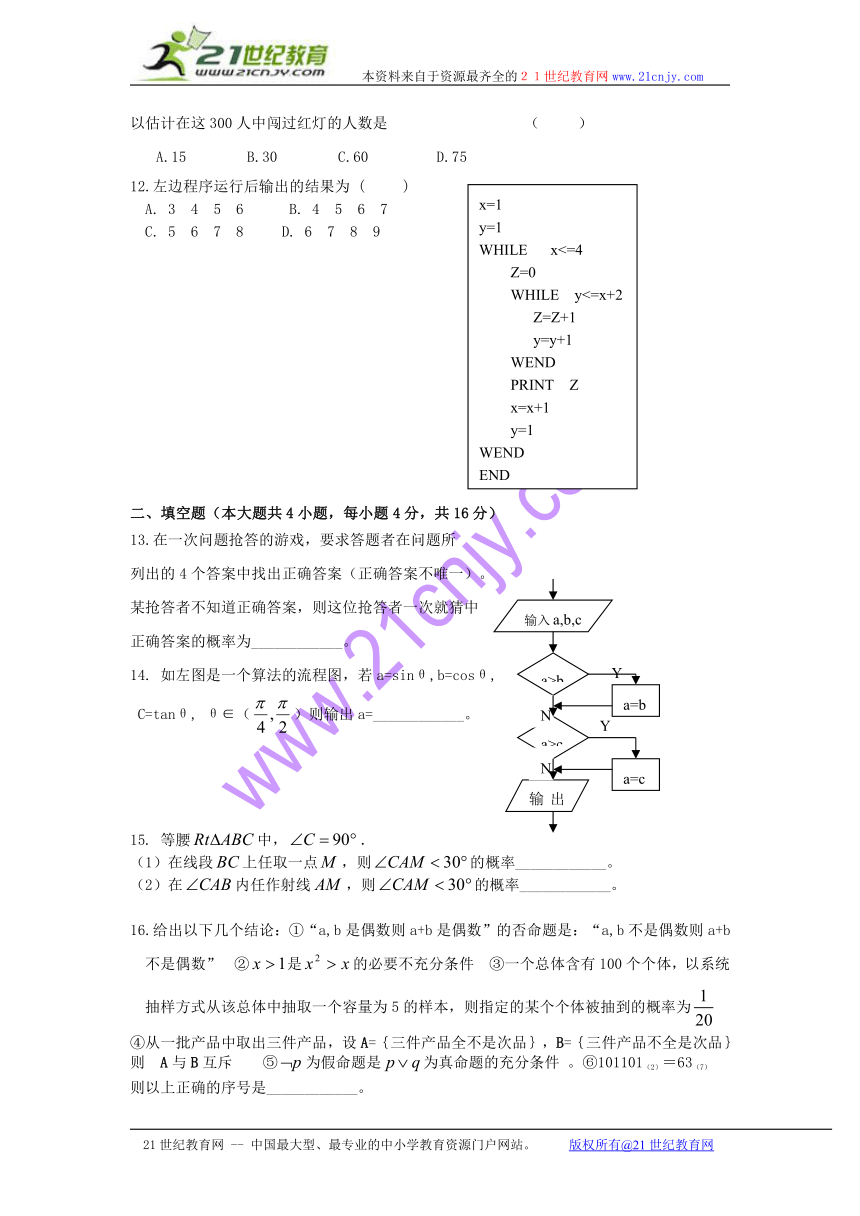
12.左边程序运行后输出的结果为 ( )
A. 3 4 5 6 B. 4 5 6 7
C. 5 6 7 8 D. 6 7 8 9
二、填空题(本大题共4小题,每小题4分,共16分)
13.在一次问题抢答的游戏,要求答题者在问题所
列出的4个答案中找出正确答案(正确答案不唯一)。
某抢答者不知道正确答案,则这位抢答者一次就猜中
正确答案的概率为____________。
14. 如左图是一个算法的流程图,若a=sinθ,b=cosθ,
C=tanθ, θ∈()则输出a=____________。
15. 等腰中,.
(1)在线段上任取一点,则的概率____________。
(2)在内任作射线,则的概率____________。
16.给出以下几个结论:①“a,b是偶数则a+b是偶数”的否命题是:“a,b不是偶数则a+b不是偶数” ②是的必要不充分条件 ③一个总体含有100个个体,以系统抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为
④从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品不全是次品}则 A与B互斥 ⑤为假命题是为真命题的充分条件 。⑥101101(2)=63(7)
则以上正确的序号是____________。
高二数学答题卷
选择题:(本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的,)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本大题共4小题,每小题4分,共16分)
13. ____________。 14. ____________。
15. ____________,____________。 16. ____________。
三、解答题(本大题共6小题:共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分14分)根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有几处错误,
请找出错误并予以更正。
18. (本小题满分12分)已知命题:若a1,则方程至少有一个正根。
(1)写出其逆命题、否命题、逆否命题。
(2)判断其逆命题是否正确,若正确,请给出证明过程;若不正确,请说明理由。
19. (本小题满分12分)设P:关于的不等式的解集是,Q:函数的定义域为,如果为真,为假,求的范围。
20.(本小题满分14分)青年歌手电视大赛共有10名选手参加,并请了7名评委。如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,程序框图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值)试根据下面所给的条件回答下列问题:
根据茎叶图,选手乙的成绩中,
众数出现的概率是多少?并根据
茎叶图分析甲、乙两人得分情况。
(至少写出两条统计结论)
在程序框图中,用k表示评委的
人数,用a表示选手的成绩(各评委
所给有效分的平均值)横线①②处应
填什么?“S1=S-max-min”的含义是什么?
根据程序框图,甲、乙的成绩分别是多少?
21.(本小题满分10分)为便民服务,某单位在行政服务中心设有一个服务窗口,该窗口每次只能接待一名顾客,今有两名顾客将在 8 小时内随机到达。顾客甲需要 1 小时服务时间,
顾客乙需要 2 小时。计算有人需要等待的概率。
22. (本小题满分14分)某种产品每箱6件,其中有2件次品,今有甲、乙两名质检员分别采用不同的方法来检测,直到发现2件次品为止。
甲:随机的拿出一件来检测,并对结果作标记,然后将其放在一边;再从剩下的产品中随机的取出一件检测同样对结果作标记后将其放在一边,以此类推…。
乙:随机的拿出一件来检测,并对结果作标记,然后将其放回箱中;再从中随机的取出一件,同样对结果作标记后并放回箱中,以此类推…。
(1)求甲检测3次才发现2件次品的概率。
(2)请设计一种用计算机(计算器)模拟(1)中甲检测3次才发现2件次品的概率。
(3)求乙检测3次才发现2件次品的概率。
试题参考答案
一、选择题答题卡(本大题共12题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
D
B
C
B
B
C
A
D
B
A
二、填空题(本大题共4题,每小题5分,共20分)
13.. (或0.0667)14.cosθ 15. , 16.③⑤⑥
三、解答题(本大题共6小题:共80分,解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分共14分)
解:(1)程序框图如图所示:……………(8分) 或者:
(2)①DO应改为WHILE;
②PRINT n+1 应改为PRINT n;
③S=1应改为S=0 ……………………………………(6分)
18. (本小题共12分)
解:(1)略 …………………(6分)
(2)正确 ……………………(6分)
19.(本小题满分12分)(略)…………(12分)
20.(本小题满分14分)
解:(1) 由图知,甲中位数是85,但极差为17分,乙中位数是84,但极差为14分,乙的成绩大致对称;甲平均分84而乙平均分85.2分可以看出乙发挥稳定性好;甲的成绩有集中在第二根茎上,而乙的成绩有集中在第二根茎上,故乙成绩较好。………(6分)
(2)①k>7 ②a=s1/5.去掉最高分与最低分,然后计算平均分。………(6分)
(3)……………………(2分)
21.(本小题满分10分)
解:设两名顾客分别在x,y时刻到达,则 记A:“有人需要等待”则画出对应的点集…0.334
22. (本小题满分14分)
解:(1)P= …… (4分)
(2)ⅰ)利用计算器(机)产生1~6的整数随机数,不妨记1、2为次品;其余为正品。
ⅱ)将上述随机数顺次3个作为一组,但剔除有数字相同的组,这样共取N组。
ⅲ)统计含有1、2的组数,记为n。
ⅳ)用表示甲检测3次才发现2件次品的概率。…… (4分)
注:若无剔除有数字相同的组,则扣除3分
(3)P= ………(5分)
高二数学试卷
一、选择题:(本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的,将答案的代号填在答案卡上)
1. 有下列四个命题:
①“若x+y =0 ,则x ,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④“不可能事件的概率为0”的逆命题;
其中的真命题为 ( )
A.①② B.②③ C.①③ D.③④
2. 将两个数A=9,B=15交换使得A=15,B=9下列语句正确的一组是( )
A. B. C. D.
3. 在下列各图中,每个图的两个变量具有相关关系的图是
(1) (2) (3) (4)
A.(1)(2) B.(1)(3) C.(2)(4) D.(2)(3)
4. 甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A. B.
C. D.
5. 用秦九韶算法计算多项式在时的值时,的值为 ( )
A. -845 B. 220 C. -57 D. 34
6. 设集合 ,则B是A的子集的一个充分不必要的条件是 ( )
A. B.
C. D.
7.某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车中抽取48辆进行检验,这三种型号的轿车依次应抽取( )
A. 16,16,16 B. 8,30,10 C. 4,33,11 D. 12,27,9
8. 已知命题:,则( )
A. B.
C. D.
9.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是
A. B. C. D.
10. 某初级中学有学生人,其中一年级人,二、三年级各人,现要利用抽样方法取人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为;使用系统抽样时,将学生统一随机编号,并将整个编号依次分为段.如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
11.为配合学校对学生进行交通安全教育,特作如下随机调查:向被调查者提出两个问题:(1)你的学号是偶数吗?(2)你是否闯过红灯?要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)问题,否则回答第(2)问题。被调查者不必告诉调查人自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道回答了哪个问题,所以都如实做了回答。如果随机调查了300人,其中有90人回答了“是”,由此可以估计在这300人中闯过红灯的人数是 ( )
A.15 B.30 C.60 D.75
12.左边程序运行后输出的结果为 ( )
A. 3 4 5 6 B. 4 5 6 7
C. 5 6 7 8 D. 6 7 8 9
二、填空题(本大题共4小题,每小题4分,共16分)
13.在一次问题抢答的游戏,要求答题者在问题所
列出的4个答案中找出正确答案(正确答案不唯一)。
某抢答者不知道正确答案,则这位抢答者一次就猜中
正确答案的概率为____________。
14. 如左图是一个算法的流程图,若a=sinθ,b=cosθ,
C=tanθ, θ∈()则输出a=____________。
15. 等腰中,.
(1)在线段上任取一点,则的概率____________。
(2)在内任作射线,则的概率____________。
16.给出以下几个结论:①“a,b是偶数则a+b是偶数”的否命题是:“a,b不是偶数则a+b不是偶数” ②是的必要不充分条件 ③一个总体含有100个个体,以系统抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为
④从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品不全是次品}则 A与B互斥 ⑤为假命题是为真命题的充分条件 。⑥101101(2)=63(7)
则以上正确的序号是____________。
高二数学答题卷
选择题:(本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的,)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本大题共4小题,每小题4分,共16分)
13. ____________。 14. ____________。
15. ____________,____________。 16. ____________。
三、解答题(本大题共6小题:共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分14分)根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有几处错误,
请找出错误并予以更正。
18. (本小题满分12分)已知命题:若a1,则方程至少有一个正根。
(1)写出其逆命题、否命题、逆否命题。
(2)判断其逆命题是否正确,若正确,请给出证明过程;若不正确,请说明理由。
19. (本小题满分12分)设P:关于的不等式的解集是,Q:函数的定义域为,如果为真,为假,求的范围。
20.(本小题满分14分)青年歌手电视大赛共有10名选手参加,并请了7名评委。如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,程序框图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值)试根据下面所给的条件回答下列问题:
根据茎叶图,选手乙的成绩中,
众数出现的概率是多少?并根据
茎叶图分析甲、乙两人得分情况。
(至少写出两条统计结论)
在程序框图中,用k表示评委的
人数,用a表示选手的成绩(各评委
所给有效分的平均值)横线①②处应
填什么?“S1=S-max-min”的含义是什么?
根据程序框图,甲、乙的成绩分别是多少?
21.(本小题满分10分)为便民服务,某单位在行政服务中心设有一个服务窗口,该窗口每次只能接待一名顾客,今有两名顾客将在 8 小时内随机到达。顾客甲需要 1 小时服务时间,
顾客乙需要 2 小时。计算有人需要等待的概率。
22. (本小题满分14分)某种产品每箱6件,其中有2件次品,今有甲、乙两名质检员分别采用不同的方法来检测,直到发现2件次品为止。
甲:随机的拿出一件来检测,并对结果作标记,然后将其放在一边;再从剩下的产品中随机的取出一件检测同样对结果作标记后将其放在一边,以此类推…。
乙:随机的拿出一件来检测,并对结果作标记,然后将其放回箱中;再从中随机的取出一件,同样对结果作标记后并放回箱中,以此类推…。
(1)求甲检测3次才发现2件次品的概率。
(2)请设计一种用计算机(计算器)模拟(1)中甲检测3次才发现2件次品的概率。
(3)求乙检测3次才发现2件次品的概率。
试题参考答案
一、选择题答题卡(本大题共12题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
D
B
C
B
B
C
A
D
B
A
二、填空题(本大题共4题,每小题5分,共20分)
13.. (或0.0667)14.cosθ 15. , 16.③⑤⑥
三、解答题(本大题共6小题:共80分,解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分共14分)
解:(1)程序框图如图所示:……………(8分) 或者:
(2)①DO应改为WHILE;
②PRINT n+1 应改为PRINT n;
③S=1应改为S=0 ……………………………………(6分)
18. (本小题共12分)
解:(1)略 …………………(6分)
(2)正确 ……………………(6分)
19.(本小题满分12分)(略)…………(12分)
20.(本小题满分14分)
解:(1) 由图知,甲中位数是85,但极差为17分,乙中位数是84,但极差为14分,乙的成绩大致对称;甲平均分84而乙平均分85.2分可以看出乙发挥稳定性好;甲的成绩有集中在第二根茎上,而乙的成绩有集中在第二根茎上,故乙成绩较好。………(6分)
(2)①k>7 ②a=s1/5.去掉最高分与最低分,然后计算平均分。………(6分)
(3)……………………(2分)
21.(本小题满分10分)
解:设两名顾客分别在x,y时刻到达,则 记A:“有人需要等待”则画出对应的点集…0.334
22. (本小题满分14分)
解:(1)P= …… (4分)
(2)ⅰ)利用计算器(机)产生1~6的整数随机数,不妨记1、2为次品;其余为正品。
ⅱ)将上述随机数顺次3个作为一组,但剔除有数字相同的组,这样共取N组。
ⅲ)统计含有1、2的组数,记为n。
ⅳ)用表示甲检测3次才发现2件次品的概率。…… (4分)
注:若无剔除有数字相同的组,则扣除3分
(3)P= ………(5分)
