二分法
图片预览






文档简介
课件17张PPT。3.1.2
用二分法求方程的近似解1、零点存在性定理:如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根2、 问1、求函数f(x)=lnx+2x- 6的零点的值 那如何计算出这个零点的值呢?如果能够把零点所在的区间范围尽量缩小,那么在一定精确度的要求下,可以得到零点的近似值.那如何缩区间范围呢?根据零点存在性定理可知,函数在(2,3)上有零点 通过用“取中点”逐步缩小零点所在的范围.
1.在区间(2,3)内,方程有解,取区间(2,3)中点2.5;
2.用计算器计算f(2.5)≈-0.084,因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内;一般地,我们把 称为区间(a,b)的中点. 3.再取区间(2.5,3)中点2.75,用计算器计算f(2.75)≈0.512,因为f(2.5)·f(2.75)<0,所以零点在区间(2.5,2.75)内.
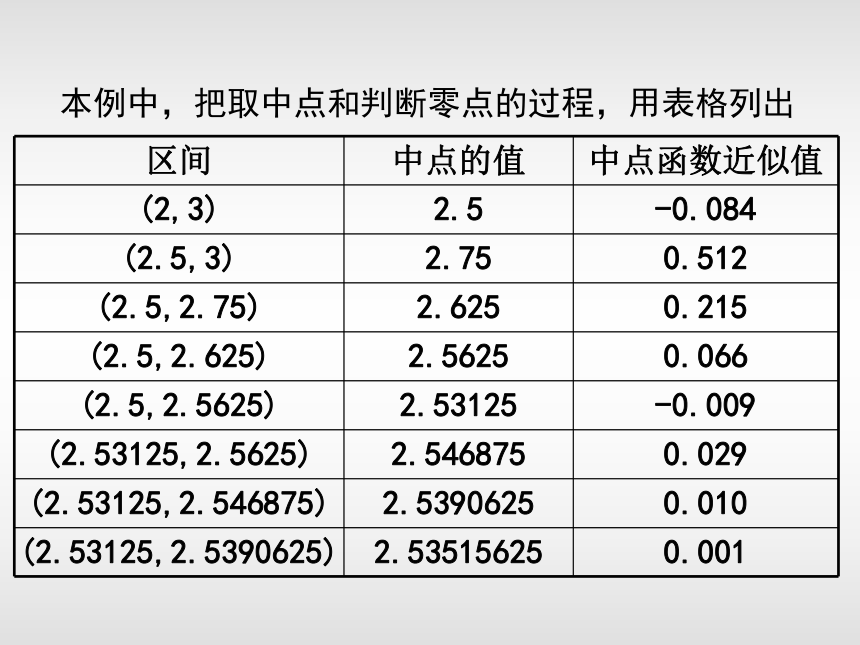
4.重复上面的过程,在有限次重复相同步骤后,零点所在区间长度在一定精度控制范围内,零点所在区间内的任意一点都可以作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.本例中,把取中点和判断零点的过程,用表格列出 精确度 :若给定一个 ,若利用二分法所求得的零点区间是(a,b),若 ,那么我们可以说在区间(a,b)内任意一个值都是零点 的满足精确度
的近似值。为方便,这里统一取区间端点a或b作为零点的近似值例、求函数f(x)=lnx+2x- 6的零点的值(精确度到0.1)那么我们就可以说2.5625或者2.5说成是零点的近似值二分法 :
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).体现了数学的逼近思想.二分法的计算步骤
给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2.求区间(a,b)的中点c;
3.计算f(c); (1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c))
(3)若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b))
4.判断:区间长度是否达到精确度ε?
即若|a-b|<ε,则得到零点近似值a(或b);否则重复2—4.课堂例题例1. 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1)解:原方程即2x+3x-7=0,令f(x)=2x+3x-7,用计算器或计算机先作出函数f(x)=2x+3x-7的对应值表 根据所列的对应值表和图象可知,f(1)·f(2)<0,说明这个函数在区间(1,2)内有零点x0.
取区间(1,2)的中点x1=1.5,用计算器可算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5).
再取(1,1.5)的中点x2=1.25,用计算器可算得f(1.25)≈-0.87.因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5). 同理可得,x0∈(1.375,1.5),x0∈(1.375,1.4375).
由于|1.375-1.4375|=0.0625<0.1,
此时,区间(1.375,1.4375)的两个端点精确到0.1的近似值都是1.4.
所以,原方程精确到0.1的近似解为1.4. 下列函数的图象与x轴均有交点,其中不能用二分法求
其零点的是( )CB已知图象连续不断的函数y=f(x)在区间(0,0.1)上有唯一零点,如果用“二分法”求这个零点(精确度为0.01)的近似值,则应将区间(0,0.1)等分的次数至少为( )
A.3 B.4 C.5 D.6B课堂小结 1.二分法的理论依据是什么?
二分法的理论依据是:如果函数y=f(x)在闭区间[a,b]上连续不断,且f(a)·f(b)<0,那么一定存在c∈(a,b),使得f(c)=0.2.二分法求零点近似值的步骤运用的数学思想:函数方程思想;数形结合思想;逼近思想
用二分法求方程的近似解1、零点存在性定理:如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根2、 问1、求函数f(x)=lnx+2x- 6的零点的值 那如何计算出这个零点的值呢?如果能够把零点所在的区间范围尽量缩小,那么在一定精确度的要求下,可以得到零点的近似值.那如何缩区间范围呢?根据零点存在性定理可知,函数在(2,3)上有零点 通过用“取中点”逐步缩小零点所在的范围.
1.在区间(2,3)内,方程有解,取区间(2,3)中点2.5;
2.用计算器计算f(2.5)≈-0.084,因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内;一般地,我们把 称为区间(a,b)的中点. 3.再取区间(2.5,3)中点2.75,用计算器计算f(2.75)≈0.512,因为f(2.5)·f(2.75)<0,所以零点在区间(2.5,2.75)内.
4.重复上面的过程,在有限次重复相同步骤后,零点所在区间长度在一定精度控制范围内,零点所在区间内的任意一点都可以作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.本例中,把取中点和判断零点的过程,用表格列出 精确度 :若给定一个 ,若利用二分法所求得的零点区间是(a,b),若 ,那么我们可以说在区间(a,b)内任意一个值都是零点 的满足精确度
的近似值。为方便,这里统一取区间端点a或b作为零点的近似值例、求函数f(x)=lnx+2x- 6的零点的值(精确度到0.1)那么我们就可以说2.5625或者2.5说成是零点的近似值二分法 :
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).体现了数学的逼近思想.二分法的计算步骤
给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2.求区间(a,b)的中点c;
3.计算f(c); (1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c))
(3)若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b))
4.判断:区间长度是否达到精确度ε?
即若|a-b|<ε,则得到零点近似值a(或b);否则重复2—4.课堂例题例1. 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1)解:原方程即2x+3x-7=0,令f(x)=2x+3x-7,用计算器或计算机先作出函数f(x)=2x+3x-7的对应值表 根据所列的对应值表和图象可知,f(1)·f(2)<0,说明这个函数在区间(1,2)内有零点x0.
取区间(1,2)的中点x1=1.5,用计算器可算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5).
再取(1,1.5)的中点x2=1.25,用计算器可算得f(1.25)≈-0.87.因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5). 同理可得,x0∈(1.375,1.5),x0∈(1.375,1.4375).
由于|1.375-1.4375|=0.0625<0.1,
此时,区间(1.375,1.4375)的两个端点精确到0.1的近似值都是1.4.
所以,原方程精确到0.1的近似解为1.4. 下列函数的图象与x轴均有交点,其中不能用二分法求
其零点的是( )CB已知图象连续不断的函数y=f(x)在区间(0,0.1)上有唯一零点,如果用“二分法”求这个零点(精确度为0.01)的近似值,则应将区间(0,0.1)等分的次数至少为( )
A.3 B.4 C.5 D.6B课堂小结 1.二分法的理论依据是什么?
二分法的理论依据是:如果函数y=f(x)在闭区间[a,b]上连续不断,且f(a)·f(b)<0,那么一定存在c∈(a,b),使得f(c)=0.2.二分法求零点近似值的步骤运用的数学思想:函数方程思想;数形结合思想;逼近思想
