25.2用列举法求概率 人教版初中数学九年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 25.2用列举法求概率 人教版初中数学九年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 686.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 05:27:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
25.2用列举法求概率人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )
A. B. C. D.
2.一个盒子中装有标号为,,,,的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于的概率为( )
A. B. C. D.
3.某公园有,,,四个入口,每个游客都是随机从一个入口进入公园,则甲、乙两位游客恰好从同一个入口进入公园的概率是( )
A. B. C. D.
4.一项“过关游戏”规定:在过第关时要将一颗质地均匀的骰子六个面上分别刻有到的点数抛掷次,若次抛掷所出现的点数之和大于,则算过关;否则不算过关.则能过第二关的概率是( )
A. B. C. D.
5.学生甲与学生乙玩一种转盘游戏.如图所示为两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字,,,表示.固定指针,同时转动两个转盘,任其自由停止.若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向分界线,则重转.在该游戏中,乙获胜的概率是( )
A. B. C. D.
6.妙妙上学经过两个路口,如果每个路口可直接通过和需等待的可能性相等,那么妙妙上学时在这两个路口都直接通过的概率为( )
A. B. C. D.
7.如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点的概率是( )
A. B. C. D.
8.为丰富学生的校园生活,各校积极开展课后服务项目某校设置了篮球、足球、乒乓球、羽毛球四个球类项目,每个同学可选择其中一个项目,问:小明和小王同时选中同一个项目的概率是( )
A. B. C. D.
9.五一期间,某商场设计了一个“玩转盘,享优惠”活动:如图所示的转盘盘面被分成四个相等的扇形区域,并分别标有文字满江红、红旗渠、殷墟、大峡谷若转动转盘两次,每次转盘停止后指针所指区域都是“满江红”,将获得一张优惠券当指针恰好指在分界线上时重转小王转动转盘两次,获得优惠券的概率为( )
A. B. C. D.
10.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别随机摸出一个小球后,放回并摇匀,再随机摸出一个,则两次都摸到相同颜色的小球的概率是( )
A. B. C. D.
11.小敏购买了一套“龙行龘龘”艺术书签外包装完全相同,分别为“招财祥龙”“瑞狮福龙”“龙凤呈祥”“锦鲤旺龙”四种不同的主题.小敏从中拿两个送给同学,先随机抽取一个不放回,再从中随机抽取一个,则恰好抽到书签“招财祥龙”和“龙凤呈祥”的概率为( )
A. B. C. D.
12.将分别标有“创”“新”“合”“肥”汉字的四个小球装在一个不透明的袋子中,这些小球除汉字外无其他差别.随机摸出两个,摸出的小球上的汉字能组成“合肥”的概率是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.下列不透明布袋中有若干个球,它们除颜色外无其他差别.
一个布袋中有个红球、个白球,先随机摸出一个球,记下颜色后放回搅匀,再随机摸出一个球,则两个球颜色不同的概率是 ;
一个布袋中有个红球、个白球,随机摸出一个球后不放回,再随机摸出一个球,则两个球颜色不同的概率是 ;
两个布袋,一个布袋中有个红球、个白球,另一个布袋中有个黄球、个红球,从两个布袋中各随机摸出个球,则摸出的两个球颜色相同的概率是 .
14.从,,,四个数中,随机抽取两个数相乘,积为大于小于的概率是 .
15.从、、、四个数中随机取一个数,不放回,再随机取一个数,把第一个数作为十位数字,第二个数作为个位数字,组成一个两位数,则这个两位数是奇数的概率是 .
16.盒子里有张形状、大小、质地完全相同的卡片,上面分别标着数字,,,从中随机抽出张后不放回,再随机抽出张,则两次抽出的卡片上的数字之和为偶数的概率是 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了解疫情期间学生网络学习的学习效果,东坡中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题:
这次活动共抽查了______人.
将条形统计图补充完整,并计算出扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数.
张老师在班上随机抽取了名学生,其中学习效果“优秀”的人,“良好”的人,“一般”的人,若再从这人中随机抽取人,请用画树状图法,求出抽取的人学习效果全是“良好”的概率.
18.本小题分
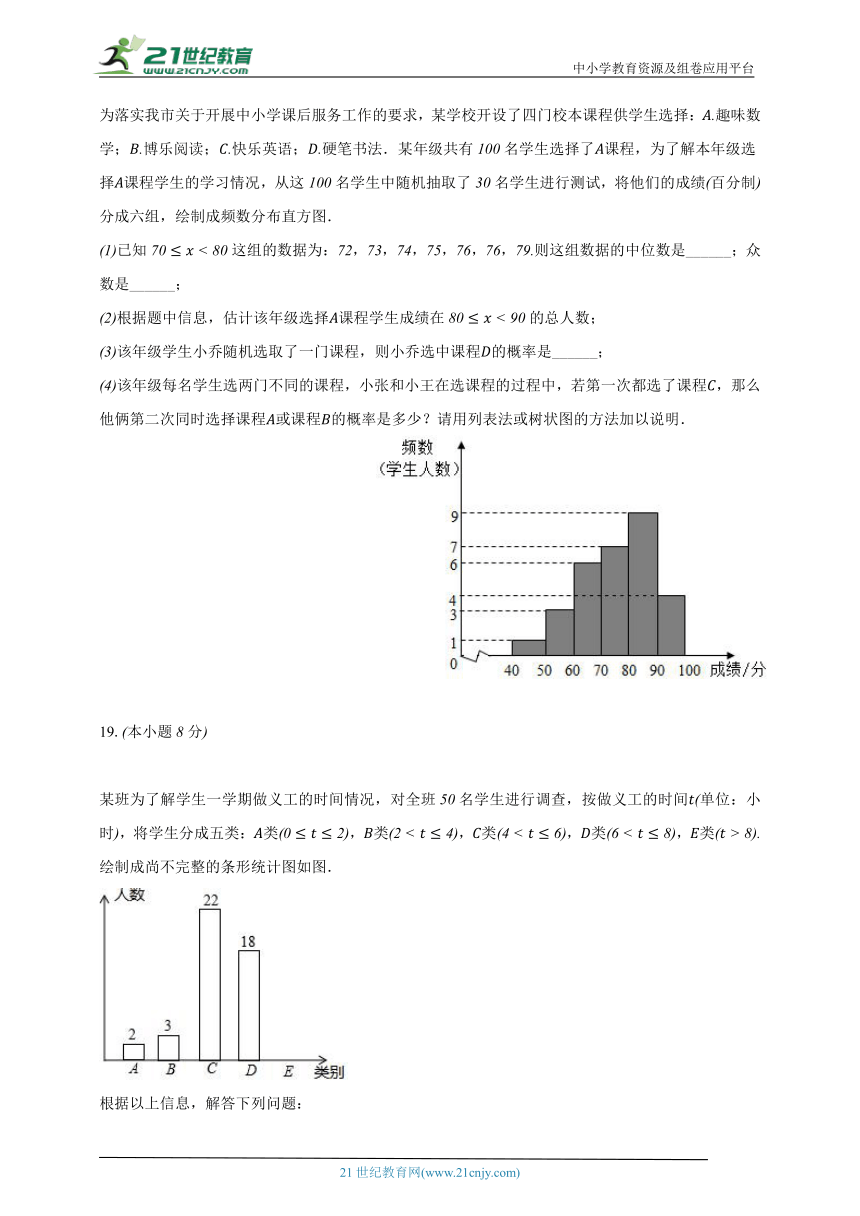
为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:趣味数学;博乐阅读;快乐英语;硬笔书法.某年级共有名学生选择了课程,为了解本年级选择课程学生的学习情况,从这名学生中随机抽取了名学生进行测试,将他们的成绩百分制分成六组,绘制成频数分布直方图.
已知这组的数据为:,,,,,,则这组数据的中位数是______;众数是______;
根据题中信息,估计该年级选择课程学生成绩在的总人数;
该年级学生小乔随机选取了一门课程,则小乔选中课程的概率是______;
该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程,那么他俩第二次同时选择课程或课程的概率是多少?请用列表法或树状图的方法加以说明.
19.本小题分
某班为了解学生一学期做义工的时间情况,对全班名学生进行调查,按做义工的时间单位:小时,将学生分成五类:类,类,类,类,类绘制成尚不完整的条形统计图如图.
根据以上信息,解答下列问题:
类学生有______人,补全条形统计图;
类学生人数占被调查总人数的______;
从该班做义工时间在的学生中任选人,求这人做义工时间都在中的概率.
20.本小题分
年月,市从甲、乙两校各抽取名学生参加全市语文素养水平监测.
【学科测试】每名学生从套不同的试卷中随机抽取套作答,小亮、小莹都参加测试,请用树状图或列表法求小亮、小莹作答相同试卷的概率.
样本学生语文测试成绩满分分如下表:
样本学生成绩 平均数 方差 中位数 众数
甲校
乙校
表中______;______.
请从平均数、方差、中位数、众数中选择合适的统计量,评判甲、乙两校样本学生的语文测试成绩.
【问卷调查】对样本学生每年阅读课外书的数量进行问卷调查,根据调查结果把样本学生分为组,制成频数分布直方图,如图所示.
组:;组:;组:.
请分别估算两校样本学生阅读课外书的平均数量取各组上限与下限的中间值近似表示该组的平均数.
【监测反思】
请用【学科测试】和【问卷调查】中的数据,解释语文测试成绩与课外阅读量的相关性;
若甲、乙两校学生都超过人,按照市的抽样方法,用样本学生数据估计甲、乙两校总体语文素养水平可行吗?为什么?
21.本小题分
某校为了了解全校学生线上学习情况,随机选取该校部分学生,调查学生居家学习时每天学习时间包括线上听课及完成作业时间如图是根据调查结果绘制的统计图表.请你根据图表中的信息完成下列问题:
频数分布表
学习时间分组 频数 频率
组
组
组
组
组
频数分布表中______,______,并将频数分布直方图补充完整;
若该校有学生名,现要对每天学习时间低于小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?
已知调查的组学生中有名男生名女生,老师随机从中选取名学生进一步了解学生居家学习情况.请用树状图或列表求所选名学生恰为一男生一女生的概率.
22.本小题分
随着电视剧去有风的地方的热播,“跟着许红豆吃大理鲜花饼”“今年春节一起来云南旅游”“总要去一趟有风的地方”等相关话题词席卷各大社交平台,剧集的热播让云南的风吹进了都市人的心头小芳和小刚分别从电视剧取景地:沙溪古镇、:凤阳邑村、:喜州古镇、:海舌公园中随机选择一处进行旅游打卡.
小芳在这个取景地中随机前往处进行旅游打卡,则她选中沙溪古镇的概率为______;
请用列表法或树状图法中的一种方法,求小芳和小刚恰好选择同一个取景地打卡的概率.
23.本小题分
为庆祝中国共产党成立周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”该市一中学经过初选,在七年级选出名同学,其中名女生,分别记为、,名男生,记为;在八年级选出名同学,其中名女生,记为,名男生,分别记为、现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.
用列表法或树状图法树状图也称树形图中的一种方法,求所有可能出现的代表队总数;
求选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
24.本小题分
为了解某县年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按,,,四个等级进行统计分析,并绘制了如下尚不完整的统计图.
请根据以上统计图提供的信息,解答下列问题:
本次抽取的学生有 名;请补全条形统计图;
根据调查结果,请估计该县名初中毕业生数学质量检测成绩为级的人数是多少?
等级中有甲、乙、丙、丁名学生成绩并列第一,现在要从这位学生中抽取名学生在校进行学习经验介绍,用树状图或列表格求出恰好选中甲乙两位学生的概率.
25.本小题分
年,黄冈、咸宁、孝感三市实行中考联合命题,为确保联合命题的公平性,决定采取三轮抽签的方式来确定各市选派命题组长的学科第一轮,各市从语文、数学、英语三个学科中随机抽取一科;第二轮,各市从物理、化学、历史三个学科中随机抽取一科;第三轮,各市从道德与法治、地理、生物三个学科中随机抽取一科.
黄冈在第一轮抽到语文学科的概率是______;
用画树状图或列表法求黄冈在第二轮和第三轮抽签中,抽到的学科恰好是历史和地理的概率.
答案和解析
1.【答案】
【解析】【分析】
本题考查用树状图或列表法求等可能事件发生的概率,关键是列举出所有等可能出现的结果数,然后用概率公式求解即可,同时注意“放回”与“不放回”的区别.
用列表法或树状图法可以列举出所有等可能出现的结果,然后看符合条件的占总数的几分之几即可.
【解答】
解:两次摸球的所有的可能性树状图如下:
两次都是红球.
故选D.
2.【答案】
【解析】解:列表如图所示:
共有种等可能的结果,两次摸出的小球的标号之和大于的有种结果,
两次摸出的小球的标号之和大于的概率为;
故选:.
首先根据题意列出表格,然后由表格求得所有等可能的结果与两次摸出的小球的标号之和大于的情况,再利用概率公式即可求得答案.
本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率所求情况数与总情况数之比.
3.【答案】
【解析】【分析】
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式求事件或的概率.
画树状图列出所有等可能结果,从中确定出甲、乙两位游客恰好从同一个入口进入公园的结果数,再利用概率公式计算可得.
【解答】
解:画树状图如下:
由树状图知共有种等可能结果,其中甲、乙两位游客恰好从同一个入口进入公园的结果有种,
所以甲、乙两位游客恰好从同一个入口进入公园的概率为.
故选B
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】解:根据题意画图如下:
共有种等可能结果,其中小明上学时在这三个路口都直接通过的只有种结果,
所以小明上学时在这两个路口都直接通过的概率为,
故选:.
根据题意先画出树状图得出所有等可能的结果数和在这两个路口都直接通过的结果数,然后根据概率公式即可得出答案.
此题考查的是用树状图法求概率,树状图法适用于两步或两步以上完成的事件.解题时注意:概率所求情况数与总情况数之比.
7.【答案】
【解析】解:将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,列表如下,
、 、 、
、 、 、
、 、 、
由表可知共有种等可能结果,其中所选矩形含点的有、;、;、;、这种结果,
所选矩形含点的概率为,
故选:.
将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,再从中找到所选矩形含点的的情况,继而利用概率公式可得答案.
本题主要考查列表法与树状图法,解题的关键是利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,并从所有结果中找到符合条件的结果数.
8.【答案】
【解析】【分析】
本题主要考查的是用列举法求概率的有关知识,篮球、足球、乒乓球和羽毛球这四个活动项目依次用、、、表示,列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解答】
解:篮球、足球、乒乓球和羽毛球这四个活动项目依次用、、、表示,
列表如下:
共有种等可能的结果数,其中小明和小王同时选中同一个项目有种结果,
小明和小王同时选中同一个项目的概率为.
9.【答案】
【解析】解:满江红、红旗渠、殷墟、大峡谷分别用数字、、、表示,
根据题意画树状图如下:
可知共有种情况,两次都是的只有一种情况,
所以小王转动转盘两次,获得优惠券的概率为.
故选:.
画树状图得出所有等可能的结果数和两次转盘停止后指针所指区域都是“满江红”的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
10.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,其中两次都摸到相同颜色的小球的结果有种,
两次都摸到相同颜色的小球的概率为.
故选:.
画树状图得出所有等可能的结果数和两次都摸到相同颜色的小球的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
11.【答案】
【解析】【分析】
解:设“招财祥龙”为,“瑞狮福龙”为,“龙凤呈祥”为,“锦鲤旺龙”为,树形图如下:
共有种等可能结果,其中同时抽到的结果有次,所以恰好抽到书签“招财祥龙”和“龙凤呈祥”的概率为,
故选:.
【解答】
本题考查了概率,解题的关键是利用树形图分析出所有等可能结果.
列出树状图,求解概率即可.
12.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,两次摸出的球上的汉字能组成“合肥”的结果有种,
两次摸出的球上的汉字能组成“合肥”的概率为,
故选:.
画树状图,共有种等可能的结果,两次摸出的球上的汉字能组成“合肥”的结果有种,再由概率公式求解即可.
此题考查了树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
13.【答案】【小题】
【小题】
【小题】
【解析】 略
略
略
14.【答案】
【解析】【分析】
列表得出所有等可能结果,从中找到积为大于小于的结果数,根据概率公式计算可得.
此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:列表如下:
由表可知,共有种等可能结果,其中积为大于小于的有种结果,
积为大于小于的概率为,
故答案为:.
15.【答案】
【解析】【分析】
画树状图,共有种等可能的结果,其中组成的两位数是奇数的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:画树状图如下:
共有种等可能的结果,其中组成的两位数是奇数的结果有种,
这个两位数是奇数的概率为,
故答案为:.
16.【答案】
【解析】【分析】
画树状图,共有种等可能的结果,两次抽出的卡片上的数字之和为偶数的结果有种,再由概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:画树状图如图:
共有种等可能的结果,两次抽出的卡片上的数字之和为偶数的结果有种,
两次抽出的卡片上的数字之和为偶数的概率为,
故答案为:.
17.【答案】;
解:“不合格”的学生人数为人,
将条形统计图补充完整如图:
学习效果“一般”的学生人数所在扇形的圆心角度数为;
解:把学习效果“优秀”的记为,“良好”记为,“一般”的记为,
画树状图如图:
共有个等可能的结果,抽取的人学习效果全是“良好”的结果有个,
抽取的人学习效果全是“良好”的概率为.
【解析】【分析】
本题考查了画树状图法求概率、概率公式以及条形统计图和扇形统计图的有关知识.画树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.注意概率所求情况数与总情况数之比.
由“良好”的人数及其所占百分比可得总人数;
求出“不合格”的学生人数为人,从而补全条形统计图;由乘以学习效果“一般”的学生人数所占的百分比即可;
画出树状图,利用概率公式求解即可.
【解答】
解:这次活动共抽查的学生人数为人,
故答案为:;
见答案;
见答案.
18.【答案】
【解析】解:在,,,,,,这组已经按从小到大排列好的数据中,中位数为,众数为;
故答案为:,;
观察直方图,抽取的名学生成绩在范围内选取课程的有人,所占比为,
那么估计该年级名学生,学生成绩在范围内,选取课程的总人数为人;
因为学校开设了四门校本课程供学生选择,小乔随机选取一门课程,则他选中课程的概率为;
故答案为:;
因该年级每名学生选两门不同的课程,第一次都选了课程,列树状图如下:
等可能结果共有种,他俩第二次同时选择课程或课程的有种,
所以,他俩第二次同时选择课程或课程的概率是.
根据中位数和众数的定义求解即可;
利用样本估计总体的方法即可估计该年级选择课程学生成绩在的总人数;
直接利用概率公式计算;
画树状图展示所有种等可能的结果数,找出他俩第二次选课相同的结果数,然后根据概率公式计算.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
19.【答案】解:;
补全图形如下:
记内的两人为甲、乙,内的人记为、、,
从中任选两人有:甲乙、甲、甲、甲、乙、乙、乙、、、这种可能结果,
其中人做义工时间都在中的有、、这种结果,
这人做义工时间都在中的概率为.
【解析】【分析】
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果数目,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.也考查条形统计图.
根据总人数等于各类别人数之和可得类别学生数;
用类别学生数除以总人数即可得;
列举所有等可能结果,根据概率公式求解可得.
【解答】
解:类学生有人,
补全图形如下:
故答案为:;
类学生人数占被调查总人数的,
故答案为:;
见答案.
20.【答案】解:【学科测试】
设套不同的试卷分别为,,,列表如下:
一共有种等可能的情况,而满足题意的有种情况,
小亮、小莹作答相同试卷的概率为;
将甲校样本学生成绩从小到大排序为:,,,,,,,,,,
位于第个和第个的数据分别是和,
,
在乙校样本学生成绩中出现次数最多的是,
,
故答案为:,;
由题意,甲、乙两校样本学生语文测试成绩的平均数相同,乙校方差小于甲校,
乙校成绩更加稳定;
【问卷调查】
由题意,甲校学生阅读课外书的平均数量为本,
乙校学生阅读课外书的平均数量为本;
【监测反思】
甲校样本学生阅读课外书的平均数量为本,乙校样本学生阅读课外书的平均数量为本;
从语文测试成绩来看,甲、乙两校平均数一样大,乙校样本学生成绩比较稳定,甲校的中位数比乙校高,但从众数来看乙校成绩要好一些;
从课外阅读量来看,虽然甲校学生阅读课外书数量的平均数较大,但整体来看,三个组的人数差别较大,没有乙校平稳;
综上来说,课外阅读量越大,语文成绩就会好一些,所以要尽可能地增加课外阅读量;
甲、乙两校学生都超过人,不可以按照市的抽样方法,用样本学生数据估计甲、乙两校总体语文素养水平,因为市的抽样方法是各校抽取了人,样本容量较小,而甲、乙两校的学生人数太多,评估出来的数据不够精确,所以不能用这个人的成绩来评估全校超过人的成绩.
【解析】【分析】
本题是统计综合题,解题的关键在于能结合频数分布直方图和数据统计表分析学生的成绩.
【学科测试】根据中位数和众数的概念分析求解,然后结合平均数、方差、中位数、众数的意义进行分析评判;
【问卷调查】根据平均数的计算公式分析计算;
【监测反思】根据表格中的数据和频数分布直方图分析语文测试成绩与课外阅读量的相关性;统计调查中确定样本容量的大小时要考虑总体的大小,从而可得结果.
【解答】
解:【学科测试】
设套不同的试卷分别为,,,列表如下:
一共有种等可能的情况,而满足题意的有种情况,
小亮、小莹作答相同试卷的概率为;
将甲校样本学生成绩从小到大排序为:,,,,,,,,,,
位于第个和第个的数据分别是和,
,
在乙校样本学生成绩中出现次数最多的是,
,
故答案为:,;
由题意,甲、乙两校样本学生语文测试成绩的平均数相同,乙校方差小于甲校,
乙校成绩更加稳定;
【问卷调查】
见答案;
【监测反思】
见答案.
21.【答案】;.
补充完整的频数分布直方图如下:
根据题意可知:
名,
答:估计全校需要提醒的学生有名;
设名男生用,表示,名女生用表示,
根据题意,画出树状图如下:
根据树状图可知:等可能的结果共有种,符合条件的有种,
所以所选名学生恰为一男生一女生的概率为:.
【解析】【分析】
本题考查了列表法与树状图法、用样本估计总体、频数分布表、频数分布直方图,解决本题的关键是掌握概率公式.
频数分布表中,,并将频数分布直方图补充完整;
若该校有学生名,现要对每天学习时间低于小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?
已知调查的组学生中有名男生名女生,老师随机从中选取名学生进一步了解学生居家学习情况.请用树状图或列表求所选名学生恰为一男生一女生的概率.
【解答】
解:根据频数分布表可知:
,
,
,
完整的频数分布直方图见答案.
故答案为:,;
见答案
见答案.
22.【答案】解:.
画树状图如下:
共有种等可能的结果,其中小芳和小刚两人选择同一个地方出游的结果有种,
小芳和小刚两人选择同一个地方出游的概率为.
【解析】根据概率公式即可得到距离;
画树状图,共有种等可能的结果,其中小芳和小刚两人选择同一个地方出游的结果有种,再由概率公式求解即可.
本题考查了列表法与树状图法;通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.
23.【答案】解:树状图如下图所示:
由上可得,出现的代表队一共有种可能性;
由可知,一共种可能性,其中一男一女出现有种,
故选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
【解析】本题考查列表法与树状图法,解答本题的关键是画出相应的树状图,求出相应的概率.
根据题意和题目中的数据,可以画出相应的树状图,并写出一共有多少种可能性;
根据中的结果和树状图,可以得到选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
24.【答案】解:
名.
补全条形统计图如下.
名.
估计该县名初中毕业生数学质量检测成绩为级的有名学生.
画树状图如下:
共有种等可能的结果,其中恰好选中甲乙两位学生的结果有种,
恰好选中甲乙两位学生的概率为.
【解析】【分析】
本题考查列表法与树状图法、条形统计图、扇形统计图,能够理解条形统计图和扇形统计图,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
用等级的人数除以其所占的百分比,即可得本次抽取的学生的人数;用本次抽取的学生的人数分别减去,,等级的人数,可求出等级的人数,补全条形统计图即可.
用乘以抽取的学生中等级所占的百分比,即可得出答案.
画树状图得出所有等可能的结果数和恰好选中甲乙两位学生的结果数,再利用概率公式可得出答案.
【解答】
解:本次抽取的学生有名.
故答案为:.
统计图见答案.
见答案.
见答案.
25.【答案】
列表如下:
物理 化学 历史
道法 物理,道法 化学,道法 历史,道法
地理 物理,地理 化学,地理 历史,地理
生物 物理,生物 化学,生物 历史,生物
由表可知共有种等可能结果,其中抽到的学科恰好是历史和地理的只有种结果,
所以抽到的学科恰好是历史和地理的概率为.
【解析】解:黄冈在第一轮抽到语文学科的概率是,
故答案为:;
见答案
直接根据概率公式求解即可;
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
25.2用列举法求概率人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )
A. B. C. D.
2.一个盒子中装有标号为,,,,的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于的概率为( )
A. B. C. D.
3.某公园有,,,四个入口,每个游客都是随机从一个入口进入公园,则甲、乙两位游客恰好从同一个入口进入公园的概率是( )
A. B. C. D.
4.一项“过关游戏”规定:在过第关时要将一颗质地均匀的骰子六个面上分别刻有到的点数抛掷次,若次抛掷所出现的点数之和大于,则算过关;否则不算过关.则能过第二关的概率是( )
A. B. C. D.
5.学生甲与学生乙玩一种转盘游戏.如图所示为两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字,,,表示.固定指针,同时转动两个转盘,任其自由停止.若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向分界线,则重转.在该游戏中,乙获胜的概率是( )
A. B. C. D.
6.妙妙上学经过两个路口,如果每个路口可直接通过和需等待的可能性相等,那么妙妙上学时在这两个路口都直接通过的概率为( )
A. B. C. D.
7.如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点的概率是( )
A. B. C. D.
8.为丰富学生的校园生活,各校积极开展课后服务项目某校设置了篮球、足球、乒乓球、羽毛球四个球类项目,每个同学可选择其中一个项目,问:小明和小王同时选中同一个项目的概率是( )
A. B. C. D.
9.五一期间,某商场设计了一个“玩转盘,享优惠”活动:如图所示的转盘盘面被分成四个相等的扇形区域,并分别标有文字满江红、红旗渠、殷墟、大峡谷若转动转盘两次,每次转盘停止后指针所指区域都是“满江红”,将获得一张优惠券当指针恰好指在分界线上时重转小王转动转盘两次,获得优惠券的概率为( )
A. B. C. D.
10.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别随机摸出一个小球后,放回并摇匀,再随机摸出一个,则两次都摸到相同颜色的小球的概率是( )
A. B. C. D.
11.小敏购买了一套“龙行龘龘”艺术书签外包装完全相同,分别为“招财祥龙”“瑞狮福龙”“龙凤呈祥”“锦鲤旺龙”四种不同的主题.小敏从中拿两个送给同学,先随机抽取一个不放回,再从中随机抽取一个,则恰好抽到书签“招财祥龙”和“龙凤呈祥”的概率为( )
A. B. C. D.
12.将分别标有“创”“新”“合”“肥”汉字的四个小球装在一个不透明的袋子中,这些小球除汉字外无其他差别.随机摸出两个,摸出的小球上的汉字能组成“合肥”的概率是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.下列不透明布袋中有若干个球,它们除颜色外无其他差别.
一个布袋中有个红球、个白球,先随机摸出一个球,记下颜色后放回搅匀,再随机摸出一个球,则两个球颜色不同的概率是 ;
一个布袋中有个红球、个白球,随机摸出一个球后不放回,再随机摸出一个球,则两个球颜色不同的概率是 ;
两个布袋,一个布袋中有个红球、个白球,另一个布袋中有个黄球、个红球,从两个布袋中各随机摸出个球,则摸出的两个球颜色相同的概率是 .
14.从,,,四个数中,随机抽取两个数相乘,积为大于小于的概率是 .
15.从、、、四个数中随机取一个数,不放回,再随机取一个数,把第一个数作为十位数字,第二个数作为个位数字,组成一个两位数,则这个两位数是奇数的概率是 .
16.盒子里有张形状、大小、质地完全相同的卡片,上面分别标着数字,,,从中随机抽出张后不放回,再随机抽出张,则两次抽出的卡片上的数字之和为偶数的概率是 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了解疫情期间学生网络学习的学习效果,东坡中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题:
这次活动共抽查了______人.
将条形统计图补充完整,并计算出扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数.
张老师在班上随机抽取了名学生,其中学习效果“优秀”的人,“良好”的人,“一般”的人,若再从这人中随机抽取人,请用画树状图法,求出抽取的人学习效果全是“良好”的概率.
18.本小题分
为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:趣味数学;博乐阅读;快乐英语;硬笔书法.某年级共有名学生选择了课程,为了解本年级选择课程学生的学习情况,从这名学生中随机抽取了名学生进行测试,将他们的成绩百分制分成六组,绘制成频数分布直方图.
已知这组的数据为:,,,,,,则这组数据的中位数是______;众数是______;
根据题中信息,估计该年级选择课程学生成绩在的总人数;
该年级学生小乔随机选取了一门课程,则小乔选中课程的概率是______;
该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程,那么他俩第二次同时选择课程或课程的概率是多少?请用列表法或树状图的方法加以说明.
19.本小题分
某班为了解学生一学期做义工的时间情况,对全班名学生进行调查,按做义工的时间单位:小时,将学生分成五类:类,类,类,类,类绘制成尚不完整的条形统计图如图.
根据以上信息,解答下列问题:
类学生有______人,补全条形统计图;
类学生人数占被调查总人数的______;
从该班做义工时间在的学生中任选人,求这人做义工时间都在中的概率.
20.本小题分
年月,市从甲、乙两校各抽取名学生参加全市语文素养水平监测.
【学科测试】每名学生从套不同的试卷中随机抽取套作答,小亮、小莹都参加测试,请用树状图或列表法求小亮、小莹作答相同试卷的概率.
样本学生语文测试成绩满分分如下表:
样本学生成绩 平均数 方差 中位数 众数
甲校
乙校
表中______;______.
请从平均数、方差、中位数、众数中选择合适的统计量,评判甲、乙两校样本学生的语文测试成绩.
【问卷调查】对样本学生每年阅读课外书的数量进行问卷调查,根据调查结果把样本学生分为组,制成频数分布直方图,如图所示.
组:;组:;组:.
请分别估算两校样本学生阅读课外书的平均数量取各组上限与下限的中间值近似表示该组的平均数.
【监测反思】
请用【学科测试】和【问卷调查】中的数据,解释语文测试成绩与课外阅读量的相关性;
若甲、乙两校学生都超过人,按照市的抽样方法,用样本学生数据估计甲、乙两校总体语文素养水平可行吗?为什么?
21.本小题分
某校为了了解全校学生线上学习情况,随机选取该校部分学生,调查学生居家学习时每天学习时间包括线上听课及完成作业时间如图是根据调查结果绘制的统计图表.请你根据图表中的信息完成下列问题:
频数分布表
学习时间分组 频数 频率
组
组
组
组
组
频数分布表中______,______,并将频数分布直方图补充完整;
若该校有学生名,现要对每天学习时间低于小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?
已知调查的组学生中有名男生名女生,老师随机从中选取名学生进一步了解学生居家学习情况.请用树状图或列表求所选名学生恰为一男生一女生的概率.
22.本小题分
随着电视剧去有风的地方的热播,“跟着许红豆吃大理鲜花饼”“今年春节一起来云南旅游”“总要去一趟有风的地方”等相关话题词席卷各大社交平台,剧集的热播让云南的风吹进了都市人的心头小芳和小刚分别从电视剧取景地:沙溪古镇、:凤阳邑村、:喜州古镇、:海舌公园中随机选择一处进行旅游打卡.
小芳在这个取景地中随机前往处进行旅游打卡,则她选中沙溪古镇的概率为______;
请用列表法或树状图法中的一种方法,求小芳和小刚恰好选择同一个取景地打卡的概率.
23.本小题分
为庆祝中国共产党成立周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”该市一中学经过初选,在七年级选出名同学,其中名女生,分别记为、,名男生,记为;在八年级选出名同学,其中名女生,记为,名男生,分别记为、现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.
用列表法或树状图法树状图也称树形图中的一种方法,求所有可能出现的代表队总数;
求选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
24.本小题分
为了解某县年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按,,,四个等级进行统计分析,并绘制了如下尚不完整的统计图.
请根据以上统计图提供的信息,解答下列问题:
本次抽取的学生有 名;请补全条形统计图;
根据调查结果,请估计该县名初中毕业生数学质量检测成绩为级的人数是多少?
等级中有甲、乙、丙、丁名学生成绩并列第一,现在要从这位学生中抽取名学生在校进行学习经验介绍,用树状图或列表格求出恰好选中甲乙两位学生的概率.
25.本小题分
年,黄冈、咸宁、孝感三市实行中考联合命题,为确保联合命题的公平性,决定采取三轮抽签的方式来确定各市选派命题组长的学科第一轮,各市从语文、数学、英语三个学科中随机抽取一科;第二轮,各市从物理、化学、历史三个学科中随机抽取一科;第三轮,各市从道德与法治、地理、生物三个学科中随机抽取一科.
黄冈在第一轮抽到语文学科的概率是______;
用画树状图或列表法求黄冈在第二轮和第三轮抽签中,抽到的学科恰好是历史和地理的概率.
答案和解析
1.【答案】
【解析】【分析】
本题考查用树状图或列表法求等可能事件发生的概率,关键是列举出所有等可能出现的结果数,然后用概率公式求解即可,同时注意“放回”与“不放回”的区别.
用列表法或树状图法可以列举出所有等可能出现的结果,然后看符合条件的占总数的几分之几即可.
【解答】
解:两次摸球的所有的可能性树状图如下:
两次都是红球.
故选D.
2.【答案】
【解析】解:列表如图所示:
共有种等可能的结果,两次摸出的小球的标号之和大于的有种结果,
两次摸出的小球的标号之和大于的概率为;
故选:.
首先根据题意列出表格,然后由表格求得所有等可能的结果与两次摸出的小球的标号之和大于的情况,再利用概率公式即可求得答案.
本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率所求情况数与总情况数之比.
3.【答案】
【解析】【分析】
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式求事件或的概率.
画树状图列出所有等可能结果,从中确定出甲、乙两位游客恰好从同一个入口进入公园的结果数,再利用概率公式计算可得.
【解答】
解:画树状图如下:
由树状图知共有种等可能结果,其中甲、乙两位游客恰好从同一个入口进入公园的结果有种,
所以甲、乙两位游客恰好从同一个入口进入公园的概率为.
故选B
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】解:根据题意画图如下:
共有种等可能结果,其中小明上学时在这三个路口都直接通过的只有种结果,
所以小明上学时在这两个路口都直接通过的概率为,
故选:.
根据题意先画出树状图得出所有等可能的结果数和在这两个路口都直接通过的结果数,然后根据概率公式即可得出答案.
此题考查的是用树状图法求概率,树状图法适用于两步或两步以上完成的事件.解题时注意:概率所求情况数与总情况数之比.
7.【答案】
【解析】解:将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,列表如下,
、 、 、
、 、 、
、 、 、
由表可知共有种等可能结果,其中所选矩形含点的有、;、;、;、这种结果,
所选矩形含点的概率为,
故选:.
将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,再从中找到所选矩形含点的的情况,继而利用概率公式可得答案.
本题主要考查列表法与树状图法,解题的关键是利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,并从所有结果中找到符合条件的结果数.
8.【答案】
【解析】【分析】
本题主要考查的是用列举法求概率的有关知识,篮球、足球、乒乓球和羽毛球这四个活动项目依次用、、、表示,列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解答】
解:篮球、足球、乒乓球和羽毛球这四个活动项目依次用、、、表示,
列表如下:
共有种等可能的结果数,其中小明和小王同时选中同一个项目有种结果,
小明和小王同时选中同一个项目的概率为.
9.【答案】
【解析】解:满江红、红旗渠、殷墟、大峡谷分别用数字、、、表示,
根据题意画树状图如下:
可知共有种情况,两次都是的只有一种情况,
所以小王转动转盘两次,获得优惠券的概率为.
故选:.
画树状图得出所有等可能的结果数和两次转盘停止后指针所指区域都是“满江红”的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
10.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,其中两次都摸到相同颜色的小球的结果有种,
两次都摸到相同颜色的小球的概率为.
故选:.
画树状图得出所有等可能的结果数和两次都摸到相同颜色的小球的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
11.【答案】
【解析】【分析】
解:设“招财祥龙”为,“瑞狮福龙”为,“龙凤呈祥”为,“锦鲤旺龙”为,树形图如下:
共有种等可能结果,其中同时抽到的结果有次,所以恰好抽到书签“招财祥龙”和“龙凤呈祥”的概率为,
故选:.
【解答】
本题考查了概率,解题的关键是利用树形图分析出所有等可能结果.
列出树状图,求解概率即可.
12.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,两次摸出的球上的汉字能组成“合肥”的结果有种,
两次摸出的球上的汉字能组成“合肥”的概率为,
故选:.
画树状图,共有种等可能的结果,两次摸出的球上的汉字能组成“合肥”的结果有种,再由概率公式求解即可.
此题考查了树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
13.【答案】【小题】
【小题】
【小题】
【解析】 略
略
略
14.【答案】
【解析】【分析】
列表得出所有等可能结果,从中找到积为大于小于的结果数,根据概率公式计算可得.
此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:列表如下:
由表可知,共有种等可能结果,其中积为大于小于的有种结果,
积为大于小于的概率为,
故答案为:.
15.【答案】
【解析】【分析】
画树状图,共有种等可能的结果,其中组成的两位数是奇数的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:画树状图如下:
共有种等可能的结果,其中组成的两位数是奇数的结果有种,
这个两位数是奇数的概率为,
故答案为:.
16.【答案】
【解析】【分析】
画树状图,共有种等可能的结果,两次抽出的卡片上的数字之和为偶数的结果有种,再由概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【解答】
解:画树状图如图:
共有种等可能的结果,两次抽出的卡片上的数字之和为偶数的结果有种,
两次抽出的卡片上的数字之和为偶数的概率为,
故答案为:.
17.【答案】;
解:“不合格”的学生人数为人,
将条形统计图补充完整如图:
学习效果“一般”的学生人数所在扇形的圆心角度数为;
解:把学习效果“优秀”的记为,“良好”记为,“一般”的记为,
画树状图如图:
共有个等可能的结果,抽取的人学习效果全是“良好”的结果有个,
抽取的人学习效果全是“良好”的概率为.
【解析】【分析】
本题考查了画树状图法求概率、概率公式以及条形统计图和扇形统计图的有关知识.画树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.注意概率所求情况数与总情况数之比.
由“良好”的人数及其所占百分比可得总人数;
求出“不合格”的学生人数为人,从而补全条形统计图;由乘以学习效果“一般”的学生人数所占的百分比即可;
画出树状图,利用概率公式求解即可.
【解答】
解:这次活动共抽查的学生人数为人,
故答案为:;
见答案;
见答案.
18.【答案】
【解析】解:在,,,,,,这组已经按从小到大排列好的数据中,中位数为,众数为;
故答案为:,;
观察直方图,抽取的名学生成绩在范围内选取课程的有人,所占比为,
那么估计该年级名学生,学生成绩在范围内,选取课程的总人数为人;
因为学校开设了四门校本课程供学生选择,小乔随机选取一门课程,则他选中课程的概率为;
故答案为:;
因该年级每名学生选两门不同的课程,第一次都选了课程,列树状图如下:
等可能结果共有种,他俩第二次同时选择课程或课程的有种,
所以,他俩第二次同时选择课程或课程的概率是.
根据中位数和众数的定义求解即可;
利用样本估计总体的方法即可估计该年级选择课程学生成绩在的总人数;
直接利用概率公式计算;
画树状图展示所有种等可能的结果数,找出他俩第二次选课相同的结果数,然后根据概率公式计算.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
19.【答案】解:;
补全图形如下:
记内的两人为甲、乙,内的人记为、、,
从中任选两人有:甲乙、甲、甲、甲、乙、乙、乙、、、这种可能结果,
其中人做义工时间都在中的有、、这种结果,
这人做义工时间都在中的概率为.
【解析】【分析】
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果数目,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.也考查条形统计图.
根据总人数等于各类别人数之和可得类别学生数;
用类别学生数除以总人数即可得;
列举所有等可能结果,根据概率公式求解可得.
【解答】
解:类学生有人,
补全图形如下:
故答案为:;
类学生人数占被调查总人数的,
故答案为:;
见答案.
20.【答案】解:【学科测试】
设套不同的试卷分别为,,,列表如下:
一共有种等可能的情况,而满足题意的有种情况,
小亮、小莹作答相同试卷的概率为;
将甲校样本学生成绩从小到大排序为:,,,,,,,,,,
位于第个和第个的数据分别是和,
,
在乙校样本学生成绩中出现次数最多的是,
,
故答案为:,;
由题意,甲、乙两校样本学生语文测试成绩的平均数相同,乙校方差小于甲校,
乙校成绩更加稳定;
【问卷调查】
由题意,甲校学生阅读课外书的平均数量为本,
乙校学生阅读课外书的平均数量为本;
【监测反思】
甲校样本学生阅读课外书的平均数量为本,乙校样本学生阅读课外书的平均数量为本;
从语文测试成绩来看,甲、乙两校平均数一样大,乙校样本学生成绩比较稳定,甲校的中位数比乙校高,但从众数来看乙校成绩要好一些;
从课外阅读量来看,虽然甲校学生阅读课外书数量的平均数较大,但整体来看,三个组的人数差别较大,没有乙校平稳;
综上来说,课外阅读量越大,语文成绩就会好一些,所以要尽可能地增加课外阅读量;
甲、乙两校学生都超过人,不可以按照市的抽样方法,用样本学生数据估计甲、乙两校总体语文素养水平,因为市的抽样方法是各校抽取了人,样本容量较小,而甲、乙两校的学生人数太多,评估出来的数据不够精确,所以不能用这个人的成绩来评估全校超过人的成绩.
【解析】【分析】
本题是统计综合题,解题的关键在于能结合频数分布直方图和数据统计表分析学生的成绩.
【学科测试】根据中位数和众数的概念分析求解,然后结合平均数、方差、中位数、众数的意义进行分析评判;
【问卷调查】根据平均数的计算公式分析计算;
【监测反思】根据表格中的数据和频数分布直方图分析语文测试成绩与课外阅读量的相关性;统计调查中确定样本容量的大小时要考虑总体的大小,从而可得结果.
【解答】
解:【学科测试】
设套不同的试卷分别为,,,列表如下:
一共有种等可能的情况,而满足题意的有种情况,
小亮、小莹作答相同试卷的概率为;
将甲校样本学生成绩从小到大排序为:,,,,,,,,,,
位于第个和第个的数据分别是和,
,
在乙校样本学生成绩中出现次数最多的是,
,
故答案为:,;
由题意,甲、乙两校样本学生语文测试成绩的平均数相同,乙校方差小于甲校,
乙校成绩更加稳定;
【问卷调查】
见答案;
【监测反思】
见答案.
21.【答案】;.
补充完整的频数分布直方图如下:
根据题意可知:
名,
答:估计全校需要提醒的学生有名;
设名男生用,表示,名女生用表示,
根据题意,画出树状图如下:
根据树状图可知:等可能的结果共有种,符合条件的有种,
所以所选名学生恰为一男生一女生的概率为:.
【解析】【分析】
本题考查了列表法与树状图法、用样本估计总体、频数分布表、频数分布直方图,解决本题的关键是掌握概率公式.
频数分布表中,,并将频数分布直方图补充完整;
若该校有学生名,现要对每天学习时间低于小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?
已知调查的组学生中有名男生名女生,老师随机从中选取名学生进一步了解学生居家学习情况.请用树状图或列表求所选名学生恰为一男生一女生的概率.
【解答】
解:根据频数分布表可知:
,
,
,
完整的频数分布直方图见答案.
故答案为:,;
见答案
见答案.
22.【答案】解:.
画树状图如下:
共有种等可能的结果,其中小芳和小刚两人选择同一个地方出游的结果有种,
小芳和小刚两人选择同一个地方出游的概率为.
【解析】根据概率公式即可得到距离;
画树状图,共有种等可能的结果,其中小芳和小刚两人选择同一个地方出游的结果有种,再由概率公式求解即可.
本题考查了列表法与树状图法;通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.
23.【答案】解:树状图如下图所示:
由上可得,出现的代表队一共有种可能性;
由可知,一共种可能性,其中一男一女出现有种,
故选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
【解析】本题考查列表法与树状图法,解答本题的关键是画出相应的树状图,求出相应的概率.
根据题意和题目中的数据,可以画出相应的树状图,并写出一共有多少种可能性;
根据中的结果和树状图,可以得到选出的代表队中的两名同学恰好是一名男生和一名女生的概率.
24.【答案】解:
名.
补全条形统计图如下.
名.
估计该县名初中毕业生数学质量检测成绩为级的有名学生.
画树状图如下:
共有种等可能的结果,其中恰好选中甲乙两位学生的结果有种,
恰好选中甲乙两位学生的概率为.
【解析】【分析】
本题考查列表法与树状图法、条形统计图、扇形统计图,能够理解条形统计图和扇形统计图,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
用等级的人数除以其所占的百分比,即可得本次抽取的学生的人数;用本次抽取的学生的人数分别减去,,等级的人数,可求出等级的人数,补全条形统计图即可.
用乘以抽取的学生中等级所占的百分比,即可得出答案.
画树状图得出所有等可能的结果数和恰好选中甲乙两位学生的结果数,再利用概率公式可得出答案.
【解答】
解:本次抽取的学生有名.
故答案为:.
统计图见答案.
见答案.
见答案.
25.【答案】
列表如下:
物理 化学 历史
道法 物理,道法 化学,道法 历史,道法
地理 物理,地理 化学,地理 历史,地理
生物 物理,生物 化学,生物 历史,生物
由表可知共有种等可能结果,其中抽到的学科恰好是历史和地理的只有种结果,
所以抽到的学科恰好是历史和地理的概率为.
【解析】解:黄冈在第一轮抽到语文学科的概率是,
故答案为:;
见答案
直接根据概率公式求解即可;
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
