21.3实际问题与一元二次方程 人教版初中数学九年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 21.3实际问题与一元二次方程 人教版初中数学九年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 491.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 06:38:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
21.3实际问题与一元二次方程人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某厂家年月份的口罩产量统计如图所示.设从月份到月份,该厂家口罩产量的平均月增长率为,根据题意可得方程( )
A. B.
C. D.
2.如图,若将左图正方形剪成四块.恰能拼成右图的矩形,设,则这个正方形的面积为( )
A. B. C. D.
3.有人患了流感后,经过两轮传染后共有人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了人,则根据题意可列方程( )
A. B. C. D.
4.某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是,设每个枝干长出个小分支,则满足的方程为( )
A. B.
C. D.
5.某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支于和小分支的总数是,则这种植物每个支干长出的小分支个数是( )
A. B. C. D.
6.如图,点阵的层数用表示,点数总和用表示,当时,的值为( )
A. B. C. D.
7.如图所示,在中,,,,点以的速度从点开始沿边向点移动,点以的速度从点开始沿边向点移动,且点,分别从点,同时出发.若有一点到达目的地,则另一点同时停止运动.要使,两点之间的距离等于,则需要经过( )
A. B. C. D. 或
8.某校准备在一块长为米,宽为米的长方形花圃内修建四条宽度相等,且与各边垂直的小路如图所示,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的倍,若四条小路所占面积为平方米,则小路的宽度为( )
A. 米 B. 米 C. 米 D. 米
9.如图,在中,,,,动点,分别从点,同时开始移动移动方向如图所示,点的速度为,点的速度为,点移动到点后停止,点也随之停止运动,当四边形的面积为时,则点运动的时间是( )
A. B. 或 C. D.
10.随着“二胎政策”出生的孩子越来越大,纷纷到了入学年龄,某校年学生数比年增长了,年新学期开学统计,该校学生数又比年增长了,设、这两年该校学生数平均增长率为,则满足的方程是( )
A. B.
C. D.
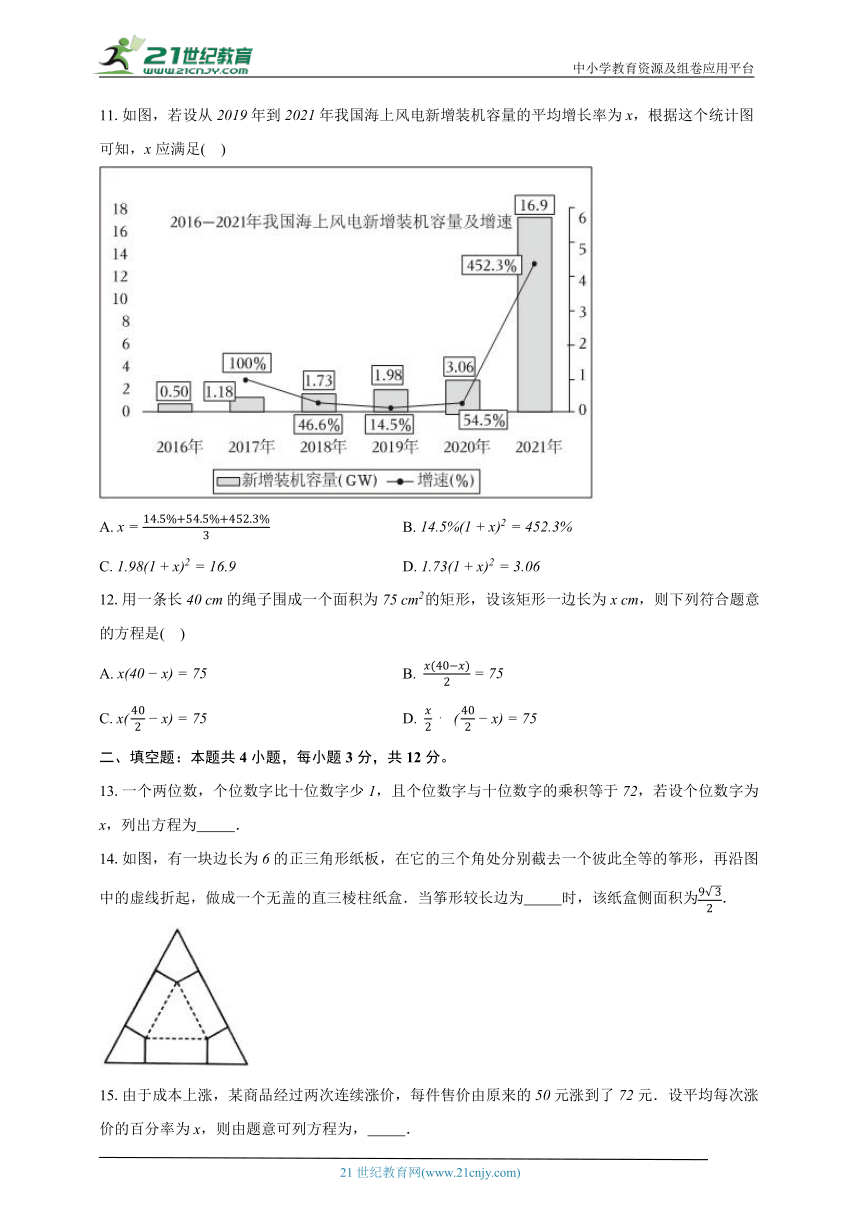
11.如图,若设从年到年我国海上风电新增装机容量的平均增长率为,根据这个统计图可知,应满足( )
A. B.
C. D.
12.用一条长的绳子围成一个面积为的矩形,设该矩形一边长为,则下列符合题意的方程是( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.一个两位数,个位数字比十位数字少,且个位数字与十位数字的乘积等于,若设个位数字为,列出方程为 .
14.如图,有一块边长为的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒.当筝形较长边为 时,该纸盒侧面积为.
15.由于成本上涨,某商品经过两次连续涨价,每件售价由原来的元涨到了元.设平均每次涨价的百分率为,则由题意可列方程为, .
16.如图,将面积为的正方形的边的长度增加,变为面积为的矩形若正方形和矩形的周长相等,则的值是 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为万元,第七天的营业额是前六天总营业额的.
求该商店去年“十一黄金周”这七天的总营业额
去年,该商店月份的营业额为万元,、月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与月份的营业额相等求该商店去年、月份营业额的月增长率.
18.本小题分
服装店经销某种品牌的童装,进价为元件,原来售价为元件,每天可以出售件,经市场调查发现每降价元,一天可以多售出件.
若想每天出售件,应降价多少元?
如果每天的利润要比原来多元,并使库存尽快地减少,问每件应降价多少元?
19.本小题分
某商店将进价为元的商品按每件元出售,每天可出售件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高元,那么每天的销售量就减少件,将每件商品提价多少元时,才能使每天的利润为元?
20.本小题分
如图,利用一面墙墙的长度为米,用米长的篱笆围成两个鸡场.中间用一道篱笆隔开,每个鸡场均留一道米宽的门,若两个鸡场总面积为平方米,求的长.
21.本小题分
为增强学生身体素质,提高学生足球运动竞技水平,某市开展“希望杯”足球比赛,赛制为单循环形式每两队之间赛一场现计划安排场比赛,应邀请多少个球队参赛?
22.本小题分
有两张长,宽的矩形纸板,分别按照图与图两种方式裁去若干小正方形和小矩形,剩余部分阴影部分恰好做成无盖和有盖的长方体纸盒各一个.
做成有盖长方体纸盒的裁剪方式是 填“图”或“图”;
已知图中裁去的小正方形边长为,求做成的纸盒的底面积;
已知按图裁剪方式做成纸盒的底面积为,,则剪去的小正方形的边长为多少?
23.本小题分
近年来,武汉市委组织部借助网红直播基地,积极探索党建引领乡村振兴的新模式.某电商对种植成本为元千克的“阳光玫瑰”葡萄进行直播销售,如果按每千克元销售,每天可卖出千克.通过市场调查发现,如果“阳光玫瑰”葡萄售价每千克降低元,日销售量将增加千克.
若每千克售价为元,每天可卖出 千克;
若日利润保持不变,每千克“阳光玫瑰”葡萄售价可降低多少元?
小明的线下水果店也销售同款葡萄,标价为每千克元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过中的售价,则该商品至少需打几折销售?
24.本小题分
为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请个好友转发,每个好友转发之后,又邀请个互不相同的好友转发,已知经过两轮转发后,共有个人参与了本次活动.
的值是多少?
再经过几轮转发后,参与人数会超过人?
25.本小题分
某商场销售一种进价为元台的台灯,经调查发现,该台灯每天的销售量台,销售单价元满足,设销售这种台灯每天的利润为元.
求与之间的函数关系式;
在保证销售量尽可能大的前提下,该商场每天还想获得元的利润,应将销售单价定位为多少元?
答案和解析
1.【答案】
【解析】解:从月份到月份,该厂家口罩产量的平均月增长率为,根据题意可得方程:,
故选:.
本题为增长率问题,一般用增长后的量增长前的量增长率,如果设这个增长率为,根据“月份的万只,月份的利润将达到万只”,即可得出方程.
本题考查了由实际问题抽象出一元二次方程,本题为增长率问题,一般形式为,为起始时间的有关数量,为终止时间的有关数量.
2.【答案】
【解析】解:由题意,得,
解得,
,
,正方形的面积故选A.
3.【答案】
【解析】解:每轮传染中平均一个人传染了人,
第一轮有人被传染,第二轮有人被传染.
根据题意得:,
故选
由每轮传染中平均一个人传染了人,可得出第一轮有人被传染,第二轮有人被传染,结合“有人患了流感后,经过两轮传染后共有人患了流感”,即可列出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
4.【答案】
【解析】【分析】
本题考查了由实际问题抽象出一元二次方程,根据主干、枝干和小分支的总数是,列出关于的一元二次方程是解题的关键.
根据每个枝干长出个小分支,则主干上长出了个枝干,根据主干、枝干和小分支的总数是,即可得出关于的一元二次方程,此题得解.
【解答】
解:设每个枝干长出个小分支,则主干上长出了个枝干,个枝干上总共长了个小分支,
根据题意得:.
故选C.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】设小路的宽度为米,则小正方形的边长为米,小路的横向总长度为米,纵向总长度为米,依题意得,整理得,解得舍去,.
9.【答案】
【解析】解:设动点,运动秒后,能使四边形的面积为,
则为,为,由三角形的面积计算公式列方程得,
,
解得,当时,,不合题意,舍去.
动点,运动秒时,能使四边形的面积为.
故选:.
设出动点,运动秒,能使四边形的面积为,用分别表示出和的长,利用三角形的面积计算公式即可解答.
此题考查一元二次方程的应用,借助三角形的面积计算公式来研究图形中的动点问题.
10.【答案】
【解析】解:设该校年学生数为,则该校年学生数为,年学生数为,
根据题意得:.
设该校年学生数为,则该校年学生数为,年学生数为,利用该校年学生数该校年学生数、这两年该校学生数平均增长率,可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
11.【答案】
【解析】解:依题意得:.
故选:.
利用年我国海上风电新增装机容量年我国海上风电新增装机容量平均增长率,即可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
12.【答案】
【解析】【分析】
本题考查了由实际问题抽象出一元二次方程,要掌握长方形的面积长宽.根据长方形的周长可以用表示另一边长,然后根据面积公式即可列出方程.
【解答】
解:设该矩形一边长为,
长方形的周长为,
宽为,
得.
故选:.
13.【答案】
【解析】【分析】设个位数字为,则十位数字为 ,再由个位数字与十位数字的乘积等于列出方程即可.
【详解】解:设个位数字为,则十位数字为 ,
由题意得 ,
故答案为: .
14.【答案】
【解析】解:三角形为等边三角形,截取的三个筝形面积相等,折叠后是一个三棱柱.设筝形较短边为,筝形较长边为,纸盒侧面积,,,,
筝形较长边为时,该纸盒侧面积为.
15.【答案】
【解析】【分析】可先表示出第一次涨价后的价格,然后可得第二次涨价后的价格,根据两次连续涨价,每件售价由原来的元涨到了元列方程即可.
【详解】解:设平均每次涨价的百分率为,
则第一次涨价后的价格为 ,第二次涨价后的价格为 ,
可列方程为 ,
故答案为: .
【点睛】此题主要考查了由实际问题抽象出一元二次方程,关键是掌握平均变化率的方法,若设变化前的量为,变化后的量为,平均变化率为,则经过两次变化后的数量关系为 .
16.【答案】
【解析】本题考查了矩形、正方形的性质,一元二次方程的应用.根据正方形的面积可得正方形的边长为,再根据正方形和矩形的周长相等,可得,再由矩形的面积建立方程求解即可得出答案.
解:正方形的面积为,
正方形的边长为,
由题意,得,
正方形和矩形的周长相等,
,
,
矩形的面积为,
,即,
解得:,
,
,
故答案为:
17.【答案】解:由题知,万元.
答:该商店去年“十一黄金周”这七天的总营业额为万元.
设该商店去年、月份营业额的月增长率为,
依题意得,
解得,不合题意,舍去,
答:该商店去年、月份营业额的月增长率为.
【解析】本题考查一元二次方程的应用.
根据该商店去年“十一黄金周”这七天的总营业额前六天的总营业额第七天的营业额,即可求出结论;
设该商店去年、月份营业额的月增长率为,根据该商店去年月份及月份的营业额,即可得出关于的一元二次方程,解之取其正值即可得出结论.
18.【答案】【小题】
解:设降价元.由题意,得,
解得.
答:应降价元;
【小题】
设降价元.由题意,得,
即,,
,.
要尽快减少库存,.
答:每件应降价元.
【解析】 见答案
见答案
19.【答案】设售价为元,,
整理得:,
,,.
故将每件售价定为或元时,才能使每天利润为元.原价为元,
元,元,
答:应将商品的售价提高元或元.
【解析】见答案
20.【答案】解:设的长为米,则边的长为米,由题意,得
,解得,,
当时,,
舍去,
当时,,
符合题意.
答:的长为米.
【解析】见答案
21.【答案】解:设应邀请个球队参赛,依题意,得,解得舍去,.
答:应邀请个球队参赛.
【解析】见答案
22.【答案】【小题】
图
【小题】
图中裁去的小正方形边长为,做成的纸盒的底面积;
【小题】
设剪去的小正方形的边长为,则有,解得或舍去,小正方形的边长为.
【解析】
解:做成有盖长方体纸盒的裁剪方式是图;
见答案
见答案
23.【答案】【小题】
【小题】
设每千克“阳光玫瑰”葡萄售价降低元,
则每千克的销售利润为元,
日销售量为千克,
根据题意,得,整理得,
解得不符合题意,舍去,.
答:若日利润保持不变,每千克“阳光玫瑰”葡萄售价可降低元;
【小题】
设该商品需要打折销售,根据题意,得,解得,
的最大值为.
答:该商品至少需打六折销售.
【解析】
解:若每千克售价为元,每天可卖出千克;
见答案
见答案
24.【答案】【小题】
解:第一轮转发了个人,第二轮转发了个人,
,
解得,舍,
的值为;
【小题】
,,
,
第四轮转发后参与人数会超过人,
再经过两轮转发后,参与人数会超过人.
【解析】 见答案
见答案
25.【答案】【小题】
解:;
【小题】
,解得,,要保证销售量尽可能大,尽量小,
应将销售单价定位为元.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.3实际问题与一元二次方程人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某厂家年月份的口罩产量统计如图所示.设从月份到月份,该厂家口罩产量的平均月增长率为,根据题意可得方程( )
A. B.
C. D.
2.如图,若将左图正方形剪成四块.恰能拼成右图的矩形,设,则这个正方形的面积为( )
A. B. C. D.
3.有人患了流感后,经过两轮传染后共有人患了流感,每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了人,则根据题意可列方程( )
A. B. C. D.
4.某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是,设每个枝干长出个小分支,则满足的方程为( )
A. B.
C. D.
5.某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支于和小分支的总数是,则这种植物每个支干长出的小分支个数是( )
A. B. C. D.
6.如图,点阵的层数用表示,点数总和用表示,当时,的值为( )
A. B. C. D.
7.如图所示,在中,,,,点以的速度从点开始沿边向点移动,点以的速度从点开始沿边向点移动,且点,分别从点,同时出发.若有一点到达目的地,则另一点同时停止运动.要使,两点之间的距离等于,则需要经过( )
A. B. C. D. 或
8.某校准备在一块长为米,宽为米的长方形花圃内修建四条宽度相等,且与各边垂直的小路如图所示,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的倍,若四条小路所占面积为平方米,则小路的宽度为( )
A. 米 B. 米 C. 米 D. 米
9.如图,在中,,,,动点,分别从点,同时开始移动移动方向如图所示,点的速度为,点的速度为,点移动到点后停止,点也随之停止运动,当四边形的面积为时,则点运动的时间是( )
A. B. 或 C. D.
10.随着“二胎政策”出生的孩子越来越大,纷纷到了入学年龄,某校年学生数比年增长了,年新学期开学统计,该校学生数又比年增长了,设、这两年该校学生数平均增长率为,则满足的方程是( )
A. B.
C. D.
11.如图,若设从年到年我国海上风电新增装机容量的平均增长率为,根据这个统计图可知,应满足( )
A. B.
C. D.
12.用一条长的绳子围成一个面积为的矩形,设该矩形一边长为,则下列符合题意的方程是( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.一个两位数,个位数字比十位数字少,且个位数字与十位数字的乘积等于,若设个位数字为,列出方程为 .
14.如图,有一块边长为的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒.当筝形较长边为 时,该纸盒侧面积为.
15.由于成本上涨,某商品经过两次连续涨价,每件售价由原来的元涨到了元.设平均每次涨价的百分率为,则由题意可列方程为, .
16.如图,将面积为的正方形的边的长度增加,变为面积为的矩形若正方形和矩形的周长相等,则的值是 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为万元,第七天的营业额是前六天总营业额的.
求该商店去年“十一黄金周”这七天的总营业额
去年,该商店月份的营业额为万元,、月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与月份的营业额相等求该商店去年、月份营业额的月增长率.
18.本小题分
服装店经销某种品牌的童装,进价为元件,原来售价为元件,每天可以出售件,经市场调查发现每降价元,一天可以多售出件.
若想每天出售件,应降价多少元?
如果每天的利润要比原来多元,并使库存尽快地减少,问每件应降价多少元?
19.本小题分
某商店将进价为元的商品按每件元出售,每天可出售件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高元,那么每天的销售量就减少件,将每件商品提价多少元时,才能使每天的利润为元?
20.本小题分
如图,利用一面墙墙的长度为米,用米长的篱笆围成两个鸡场.中间用一道篱笆隔开,每个鸡场均留一道米宽的门,若两个鸡场总面积为平方米,求的长.
21.本小题分
为增强学生身体素质,提高学生足球运动竞技水平,某市开展“希望杯”足球比赛,赛制为单循环形式每两队之间赛一场现计划安排场比赛,应邀请多少个球队参赛?
22.本小题分
有两张长,宽的矩形纸板,分别按照图与图两种方式裁去若干小正方形和小矩形,剩余部分阴影部分恰好做成无盖和有盖的长方体纸盒各一个.
做成有盖长方体纸盒的裁剪方式是 填“图”或“图”;
已知图中裁去的小正方形边长为,求做成的纸盒的底面积;
已知按图裁剪方式做成纸盒的底面积为,,则剪去的小正方形的边长为多少?
23.本小题分
近年来,武汉市委组织部借助网红直播基地,积极探索党建引领乡村振兴的新模式.某电商对种植成本为元千克的“阳光玫瑰”葡萄进行直播销售,如果按每千克元销售,每天可卖出千克.通过市场调查发现,如果“阳光玫瑰”葡萄售价每千克降低元,日销售量将增加千克.
若每千克售价为元,每天可卖出 千克;
若日利润保持不变,每千克“阳光玫瑰”葡萄售价可降低多少元?
小明的线下水果店也销售同款葡萄,标价为每千克元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过中的售价,则该商品至少需打几折销售?
24.本小题分
为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请个好友转发,每个好友转发之后,又邀请个互不相同的好友转发,已知经过两轮转发后,共有个人参与了本次活动.
的值是多少?
再经过几轮转发后,参与人数会超过人?
25.本小题分
某商场销售一种进价为元台的台灯,经调查发现,该台灯每天的销售量台,销售单价元满足,设销售这种台灯每天的利润为元.
求与之间的函数关系式;
在保证销售量尽可能大的前提下,该商场每天还想获得元的利润,应将销售单价定位为多少元?
答案和解析
1.【答案】
【解析】解:从月份到月份,该厂家口罩产量的平均月增长率为,根据题意可得方程:,
故选:.
本题为增长率问题,一般用增长后的量增长前的量增长率,如果设这个增长率为,根据“月份的万只,月份的利润将达到万只”,即可得出方程.
本题考查了由实际问题抽象出一元二次方程,本题为增长率问题,一般形式为,为起始时间的有关数量,为终止时间的有关数量.
2.【答案】
【解析】解:由题意,得,
解得,
,
,正方形的面积故选A.
3.【答案】
【解析】解:每轮传染中平均一个人传染了人,
第一轮有人被传染,第二轮有人被传染.
根据题意得:,
故选
由每轮传染中平均一个人传染了人,可得出第一轮有人被传染,第二轮有人被传染,结合“有人患了流感后,经过两轮传染后共有人患了流感”,即可列出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
4.【答案】
【解析】【分析】
本题考查了由实际问题抽象出一元二次方程,根据主干、枝干和小分支的总数是,列出关于的一元二次方程是解题的关键.
根据每个枝干长出个小分支,则主干上长出了个枝干,根据主干、枝干和小分支的总数是,即可得出关于的一元二次方程,此题得解.
【解答】
解:设每个枝干长出个小分支,则主干上长出了个枝干,个枝干上总共长了个小分支,
根据题意得:.
故选C.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】设小路的宽度为米,则小正方形的边长为米,小路的横向总长度为米,纵向总长度为米,依题意得,整理得,解得舍去,.
9.【答案】
【解析】解:设动点,运动秒后,能使四边形的面积为,
则为,为,由三角形的面积计算公式列方程得,
,
解得,当时,,不合题意,舍去.
动点,运动秒时,能使四边形的面积为.
故选:.
设出动点,运动秒,能使四边形的面积为,用分别表示出和的长,利用三角形的面积计算公式即可解答.
此题考查一元二次方程的应用,借助三角形的面积计算公式来研究图形中的动点问题.
10.【答案】
【解析】解:设该校年学生数为,则该校年学生数为,年学生数为,
根据题意得:.
设该校年学生数为,则该校年学生数为,年学生数为,利用该校年学生数该校年学生数、这两年该校学生数平均增长率,可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
11.【答案】
【解析】解:依题意得:.
故选:.
利用年我国海上风电新增装机容量年我国海上风电新增装机容量平均增长率,即可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
12.【答案】
【解析】【分析】
本题考查了由实际问题抽象出一元二次方程,要掌握长方形的面积长宽.根据长方形的周长可以用表示另一边长,然后根据面积公式即可列出方程.
【解答】
解:设该矩形一边长为,
长方形的周长为,
宽为,
得.
故选:.
13.【答案】
【解析】【分析】设个位数字为,则十位数字为 ,再由个位数字与十位数字的乘积等于列出方程即可.
【详解】解:设个位数字为,则十位数字为 ,
由题意得 ,
故答案为: .
14.【答案】
【解析】解:三角形为等边三角形,截取的三个筝形面积相等,折叠后是一个三棱柱.设筝形较短边为,筝形较长边为,纸盒侧面积,,,,
筝形较长边为时,该纸盒侧面积为.
15.【答案】
【解析】【分析】可先表示出第一次涨价后的价格,然后可得第二次涨价后的价格,根据两次连续涨价,每件售价由原来的元涨到了元列方程即可.
【详解】解:设平均每次涨价的百分率为,
则第一次涨价后的价格为 ,第二次涨价后的价格为 ,
可列方程为 ,
故答案为: .
【点睛】此题主要考查了由实际问题抽象出一元二次方程,关键是掌握平均变化率的方法,若设变化前的量为,变化后的量为,平均变化率为,则经过两次变化后的数量关系为 .
16.【答案】
【解析】本题考查了矩形、正方形的性质,一元二次方程的应用.根据正方形的面积可得正方形的边长为,再根据正方形和矩形的周长相等,可得,再由矩形的面积建立方程求解即可得出答案.
解:正方形的面积为,
正方形的边长为,
由题意,得,
正方形和矩形的周长相等,
,
,
矩形的面积为,
,即,
解得:,
,
,
故答案为:
17.【答案】解:由题知,万元.
答:该商店去年“十一黄金周”这七天的总营业额为万元.
设该商店去年、月份营业额的月增长率为,
依题意得,
解得,不合题意,舍去,
答:该商店去年、月份营业额的月增长率为.
【解析】本题考查一元二次方程的应用.
根据该商店去年“十一黄金周”这七天的总营业额前六天的总营业额第七天的营业额,即可求出结论;
设该商店去年、月份营业额的月增长率为,根据该商店去年月份及月份的营业额,即可得出关于的一元二次方程,解之取其正值即可得出结论.
18.【答案】【小题】
解:设降价元.由题意,得,
解得.
答:应降价元;
【小题】
设降价元.由题意,得,
即,,
,.
要尽快减少库存,.
答:每件应降价元.
【解析】 见答案
见答案
19.【答案】设售价为元,,
整理得:,
,,.
故将每件售价定为或元时,才能使每天利润为元.原价为元,
元,元,
答:应将商品的售价提高元或元.
【解析】见答案
20.【答案】解:设的长为米,则边的长为米,由题意,得
,解得,,
当时,,
舍去,
当时,,
符合题意.
答:的长为米.
【解析】见答案
21.【答案】解:设应邀请个球队参赛,依题意,得,解得舍去,.
答:应邀请个球队参赛.
【解析】见答案
22.【答案】【小题】
图
【小题】
图中裁去的小正方形边长为,做成的纸盒的底面积;
【小题】
设剪去的小正方形的边长为,则有,解得或舍去,小正方形的边长为.
【解析】
解:做成有盖长方体纸盒的裁剪方式是图;
见答案
见答案
23.【答案】【小题】
【小题】
设每千克“阳光玫瑰”葡萄售价降低元,
则每千克的销售利润为元,
日销售量为千克,
根据题意,得,整理得,
解得不符合题意,舍去,.
答:若日利润保持不变,每千克“阳光玫瑰”葡萄售价可降低元;
【小题】
设该商品需要打折销售,根据题意,得,解得,
的最大值为.
答:该商品至少需打六折销售.
【解析】
解:若每千克售价为元,每天可卖出千克;
见答案
见答案
24.【答案】【小题】
解:第一轮转发了个人,第二轮转发了个人,
,
解得,舍,
的值为;
【小题】
,,
,
第四轮转发后参与人数会超过人,
再经过两轮转发后,参与人数会超过人.
【解析】 见答案
见答案
25.【答案】【小题】
解:;
【小题】
,解得,,要保证销售量尽可能大,尽量小,
应将销售单价定位为元.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
