22.3实际问题与二次函数 人教版初中数学九年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 22.3实际问题与二次函数 人教版初中数学九年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 742.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 06:43:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.3实际问题与二次函数人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.长为,宽为的矩形,四个角上分别剪去边长为的小正方形,然后把四边折起来,做成底面积为的无盖的长方体盒子,则与之间的函数关系式为( )
A. B.
C. D.
2.一位篮球运动员在距离篮筐中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确落入篮筐内.已知篮筐中心距离地面高度为,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是 B. 篮筐中心的坐标是
C. 此抛物线的顶点坐标是 D. 篮球出手时离地面的高度是
3.赵州桥始建于隋代,是世界上现存年代最久远、跨度最大、保存最完整的单孔石拱桥.如图是一座仿赵州桥建造的抛物线形拱桥的示意图,正常水位时,水面宽,水位上涨到达警戒水位,此时水面宽,则正常水位时拱顶离水面的高度为( )
A. B. C. D.
4.某民俗旅游村为接待游客住宿,开设了有个床位的旅馆.若每个床位每天收费元,则床位可全部租出;若每个床位每天的收费提高元,则相应地减少了个床位的租出.如果每个床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每个床位每天最合适的收费是( )
A. 元 B. 元 C. 元 D. 元
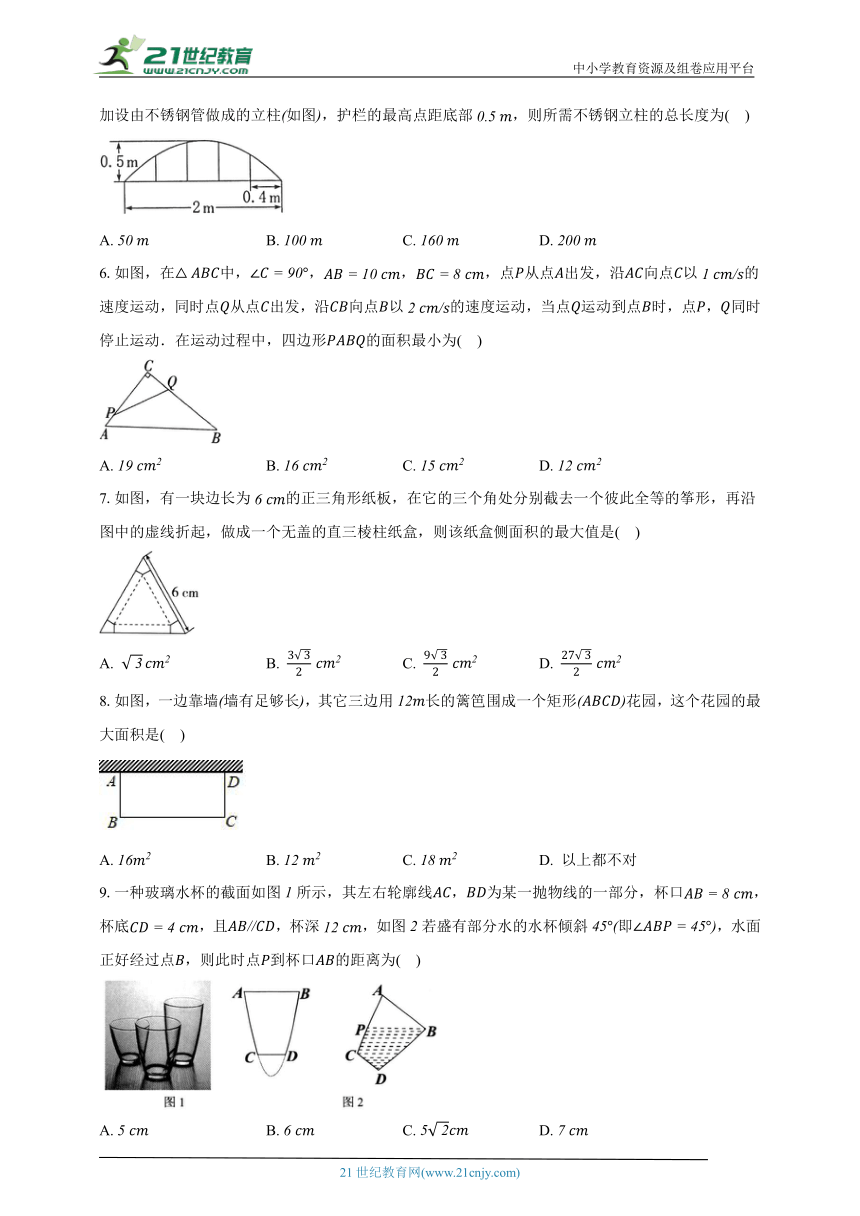
5.某公园草坪的护栏是由段形状相同的抛物线组成的,为了牢固起见,每段护栏需按间距加设由不锈钢管做成的立柱如图,护栏的最高点距底部,则所需不锈钢立柱的总长度为( )
A. B. C. D.
6.如图,在中,,,,点从点出发,沿向点以的速度运动,同时点从点出发,沿向点以的速度运动,当点运动到点时,点,同时停止运动.在运动过程中,四边形的面积最小为( )
A. B. C. D.
7.如图,有一块边长为的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A. B. C. D.
8.如图,一边靠墙墙有足够长,其它三边用长的篱笆围成一个矩形花园,这个花园的最大面积是( )
A. B. C. D. 以上都不对
9.一种玻璃水杯的截面如图所示,其左右轮廓线,为某一抛物线的一部分,杯口,杯底,且,杯深,如图若盛有部分水的水杯倾斜即,水面正好经过点,则此时点到杯口的距离为( )
A. B. C. D.
10.如图,一抛物线型拱桥,当拱顶到水面的距离为时,水面宽度为,那么水位下降时,水面的宽度为
A.
B.
C.
D.
11.如图,已知矩形中,,,对角线相交于点,抛物线经过,,三点,点是矩形内抛物线上的动点.则与面积之和的最大值是( )
A. B. C. D.
12.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长为设矩形菜园的边的长为,面积为,其中有下列结论:
的取值范围为;
的长有两个不同的值满足该矩形菜园的面积为;
矩形菜园的面积的最大值为.
其中,正确结论的个数是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,若被击打的小球飞行高度单位:与飞行时间单位:之间具有的关系为,则小球从飞出到落地所用的时间为
14.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长的栅栏,设面积为,垂直于墙的一边长为米.则关于的函数关系式: 并写出自变量的取值范围
15.如图,一块矩形土地由篱笆围着,并且由一条与边平行的篱笆分开,已知篱笆的总长为篱笆的厚度忽略不计,当 时,矩形土地的面积最大.
16.如图所示为一座抛物线形拱桥,当拱桥顶离水面时,水面宽,则水面下降时,水面宽度增加
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
某商场销售一种成本为元的商品,市场调研反映:在某个月的第天的销售价格为元,日销售量与的函数关系如图所示.
求与的函数解析式;
销售该商品第几天时,日销售利润最大?
结合函数图象回答,在当月有多少天的日销售利润大于元?
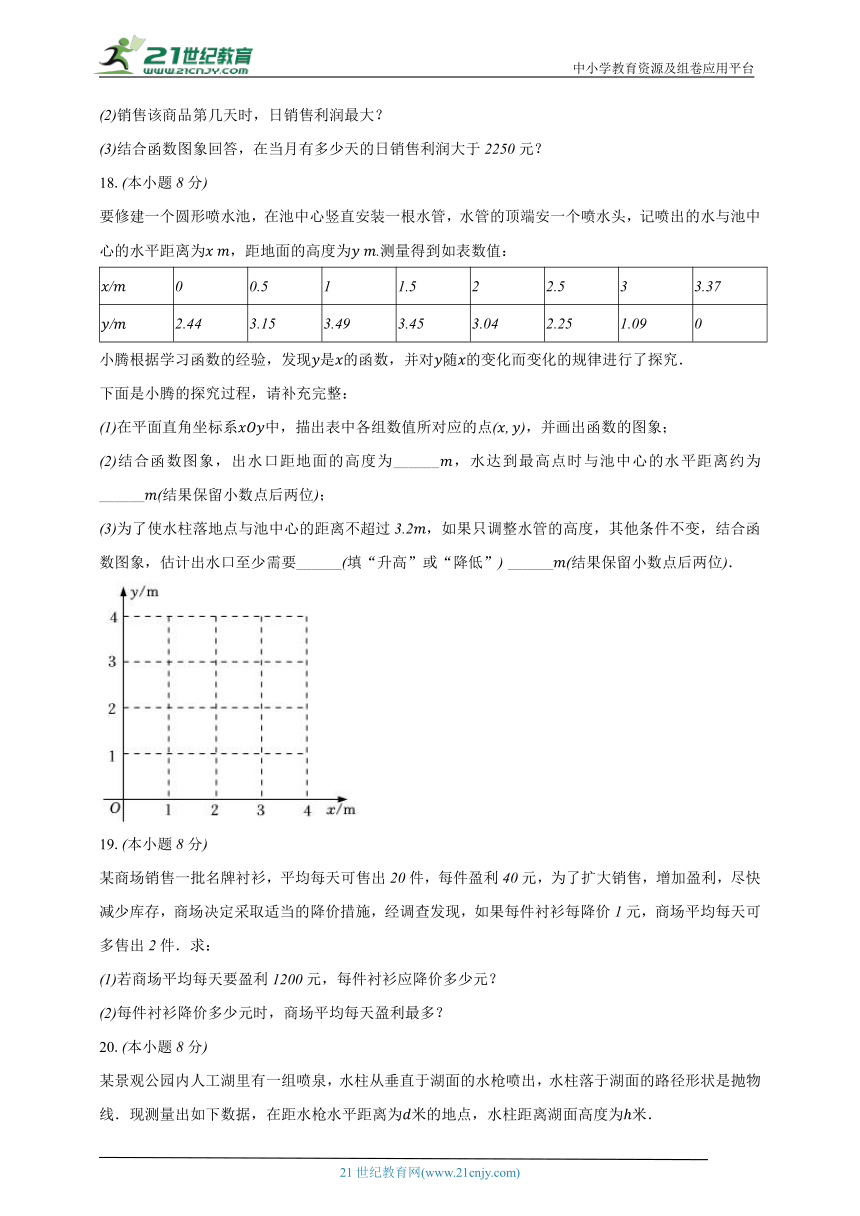
18.本小题分
要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出的水与池中心的水平距离为,距地面的高度为测量得到如表数值:
小腾根据学习函数的经验,发现是的函数,并对随的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
在平面直角坐标系中,描出表中各组数值所对应的点,并画出函数的图象;
结合函数图象,出水口距地面的高度为______,水达到最高点时与池中心的水平距离约为______结果保留小数点后两位;
为了使水柱落地点与池中心的距离不超过,如果只调整水管的高度,其他条件不变,结合函数图象,估计出水口至少需要______填“升高”或“降低” ______结果保留小数点后两位.
19.本小题分
某商场销售一批名牌衬衫,平均每天可售出件,每件盈利元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价元,商场平均每天可多售出件.求:
若商场平均每天要盈利元,每件衬衫应降价多少元?
每件衬衫降价多少元时,商场平均每天盈利最多?
20.本小题分
某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距水枪水平距离为米的地点,水柱距离湖面高度为米.
米
米
请解决以下问题:
在下边网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
请结合表中所给数据或所画图象,估出喷泉的落水点距水枪的水平距离约为______米精确到;
公园增设了新的游玩项目,购置了宽度米,顶棚到水面高度为米的平顶游船,游船从喷泉正下方通过,别有一番趣味,请通过计算说明游船是否有被喷泉淋到的危险.
21.本小题分
用各种盛水容器可以制作精致的家用流水景观如图.
科学原理:如图,始终盛满水的圆体水桶水面离地面的高度为单位:,如果在离水面竖直距离为单位:的地方开大小合适的小孔,那么从小孔射出水的射程水流落地点离小孔的水平距离单位:与的关系为.
应用思考:现用高度为的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距高处开一个小孔.
写出与的关系式;并求出当为何值时,射程有最大值,最大射程是多少?
在侧面开两个小孔,这两个小孔离水面的竖直距离分别为,,要使两孔射出水的射程相同,求,之间的关系式;
如果想通过垫高塑料水瓶,使射出水的最大射程增加,求整高的高度及小孔离水面的竖直距离.
22.本小题分
某总公司准备投资,两子公司共万元,从公司可获得的利润万元与投入资金万元满足关系,从公司可获得的利润万元与投入资金万元满足关系,万元为投资万元获得的总利润,设其中投资公司万元.
投资公司 万元,投资万元获得总利润为 万元以上两空均用表示;
求该总公司能获得的总利润的取值范围.
23.本小题分
某药店的消毒洗手液很畅销.已知该消毒洗手液的进价为每瓶元,经市场调查,每天洗手液的销售量瓶与销售单价元瓶之间满足一次函数关系,部分数据记录如表所示:
元瓶
瓶
直接写出与之间的函数关系式;不需要写自变量的取值范围
该药店的上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的设这种消毒洗手液每天的总利润为元,那么售价定为多少元时,该药店可获得的利润最大?最大利润是多少元?
24.本小题分
某地的药材批发公司指导农民种植和销售某种药材,经市场调研发现:月份这种药材每千克的售价元与月份之间存在如表所示的一次函数关系,同时,每千克的成本价元与月份之间的函数关系图象近似满足如图所示的抛物线.
月份
每千克售价元
直接写出这种药材的售价元与月份的函数关系式;
试判断几月份出售这种药材获利最大?
25.本小题分
某课外科技活动小组研制了一种航模飞行,通过实验,收集了飞机相对于出发点的飞行水平距离单位:、飞行高度单位:随飞行时间单位:的变化数据如下表:
飞机时间
飞行水平距离
飞行高度
探究发现:与,与之间的数量关系可以用我们已学过的函数来描述,直接写出关于的函数解析式和关于的函数解析式不要求写出自变量的取值范围;
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机,根据上面的探究发现解决下列问题:
若发射平台相对于安全线的高度为,求飞机落到安全线时飞行的水平距离;
在安全线上设置回收区域,,若飞机落到内不包括端点,,求发射平台相对于安全线的高度的变化范围.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】略
3.【答案】
【解析】略
4.【答案】
【解析】设每个床位每天的收费提高个元,每天的租金为元.根据题意,得为整数,当或时,有最大值.为使租出的床位少且租金高,每个床位每天最合适的收费是元.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】【分析】
本题考查了二次函数的应用及二次函数的最值,设与墙垂直的矩形的边长为 ,从而列出面积为,利用二次函数的性质求解即可.
【解答】
解:设与墙垂直的矩形的边长为 ,
则这个花园的面积是:,
当时,取得最大值,此时,
故选:.
9.【答案】
【解析】【分析】
本题考查二次函数的应用,属于较难题.
以的中点为原点建立平面直角坐标系,求得轮廓线,所在抛物线的解析式,再求得直线的解析式,联立解得点的横坐标,即可求解到杯口的距离.
【解答】
解:以的中点为原点建立平面直角坐标系,设直线与轴交点为,
,,,,
设轮廓线,所在抛物线的解析式为,
把、代入得,,
,
,直线与轴交点为,
,,
设直线的解析式为,
把、代入得,,
直线的解析式为:
由解得,舍
当,,
此时点到杯口的距离为,
故选 D.
10.【答案】
【解析】解:以拱顶所在的直线为轴,以这座抛物线型拱桥的对称轴为轴,建立直角坐标系,
设抛物线解析式为,
把代入得:,
解得:,
抛物线解析式为,
水位下降时,
拱顶到水面的距离为
把代入得:,
则水面的宽度是米,
故选:.
根据题意设抛物线解析式,求出解析式确定出水面的宽度即可.
本题主要考查二次函数的应用,熟练掌握待定系数法是解本题的关键.
11.【答案】
【解析】【分析】
本题考查了待定系数法求函数解析式、矩形的性质、三角形的面积公式以及二次函数的最值,建立直角坐标系,找出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.以点为原点,线段所在的直线为轴,线段所在的直线为轴建立直角坐标系,根据长方形的性质得出点、、三点的坐标,设抛物线的解析式为,结合点、、的坐标利用待定系数法即可求出抛物线的解析式,由点为长方形内的抛物线上的动点,设出点的坐标,结合三角形的面积公式找出关于的函数解析式,根据二次函数的性质即可得出结论.
【解答】
解:以点为原点,线段所在的直线为轴,线段所在的直线为轴建立直角坐标系,如图所示.
矩形中,,,对角线相交于点,
点的坐标为,点的坐标为,点的坐标为.
设抛物线的解析式为,
抛物线经过、、三点,
有,
解得:,
抛物线的解析式为.
点是矩形内的抛物线上的动点,
设点的坐标为,
当时,与面积之和最大,最大值为.
故选B.
12.【答案】
【解析】解:设这个菜园垂直于墙的一边的长为则的长为米,
墙长为,,
解得,
的取值范围为,
故错误;
根据题意得:,
解得,,
,
,
的长有个值满足该矩形菜园的面积为,
故错误;
根据题意得:,
,,
当时,有最大值,最大值为,
故正确.
故选:.
根据墙长为,,列不等式组,解不等式组即可求出自变量的取值范围,从而可判断;根据矩形的面积列出方程,解方程求的值,可以判断;利用二次函数求最值的知识可得出菜园的最大面积,可以判断.
此题主要考查了二次函数及一元二次方程的应用,熟练掌握最值问题的求法是解答本题的关键.
13.【答案】
【解析】【分析】
本题考查的是二次函数的应用有关知识,根据关系式,令即可求得的值为飞行的时间.
【解答】
解:依题意,令得:
,
得,
解得舍去或,
即小球从飞出到落地所用的时间为.
故答案为.
14.【答案】.
【解析】【分析】
本题主要考查二次函数的应用.根据条件得出与旧墙平行的一边的长度是解决问题的关键.
根据题意可知,三间羊圈与旧墙平行的一边的总长为,列出二次函数的关系式即可.
【解答】
解:根据题意可知,三间羊圈与旧墙平行的一边的总长为,
则: 由图可知:,,
所以的取值范围是.
故答案为:.
15.【答案】
【解析】【分析】
本题考查二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的顶点式求函数的最值.
设,矩形土地的面积为,则,进而求出与的函数关系式,将其化为顶点式求最值即可.
【解答】
解:设,矩形土地的面积为,
则,
由题意可得,
,
当时,取得最大值,此时,
,
故答案为:.
16.【答案】
【解析】略
17.【答案】【小题】
解:设,
把,代入上式得,
解得,
与的函数解析式为:
【小题】
设日销售利润为元,
由题意得:
,
,,
当时,最大,
答:销售该商品第天时,日销售利润最大.
【小题】
令,
则,
解得,,,
结合二次函数图象可知,
当时,,
有天的日销售利润大于元.
【解析】
设,根据图象取两个点坐标代入,求出,的值即可.
设日销售利润为元,列出关于的函数关系式,求最大值即可.
令,求出一元二次方程的两个解,结合二次函数的草图求出的范围,从而得到结果.
本题主要考查了一次函数的应用,二次函数的应用,读懂题意,正确列出函数关系式是解题的关键.
18.【答案】解:如图,
设,
把代入可得,
,
解得,
所以与的关系式为,
当时,;顶点坐标为,
出水口距地面的高度为,水达到最高点时与池中心的水平距离约为,
故答案为:,;
当时,,
所以出水口至少要降低米,
故答案为:降低,.
【解析】本题考查二次函数的实际应用,根据点的坐标画出函数图象是解题关键.
根据对应点画出图象即可;
根据对应点求出与的关系式即可得到答案;
把代入得到得值可得出水口要升高的高度.
19.【答案】解:设每件衬衫应降价元,则每天多销售件,由题意,得
,
解得:,,
要扩大销售,减少库存,
每件衬衫应降价元;
设商场每天的盈利为元,由题意,得
,
,
时,最大元.
答:每件衬衫应降价元时,商场平均每天盈利最多,每天最多盈利元.
【解析】本题主要考查了二次函数的应用以及一元二次方程的应用,根据数量关系列出关于的一元二次方程二次函数关系式是解题的关键.
设每件衬衫应降价元,根据“商场盈利单件盈利销售数量”,即可列出关于的一元二次方程,解方程即可得出的值,再结合减少库存即可确定的值;
设每件衬衫降价元时,商场所获得的利润为元,根据“商场盈利单件盈利销售数量”,即可找出关于的二次函数关系式,配方后根据二次函数的性质即可得出每件衬衫降价多少元时盈利最大.
20.【答案】解:如图,
由图象得,顶点,
设,
把代入可得,
,
当时,,
解得或舍去,
米,
答:喷泉的落水点距水枪的水平距离约为米,
故答案为:;
当时,,
答:游船有被喷泉淋到的危险.
【解析】本题考查二次函数的实际应用,根据对应点的坐标得到二次函数关系式是解题关键.
根据对应点画图象即可;
求出二次函数的关系式,把代入即可;
把代入二次函数关系式得到得值,再与比较即可.
21.【答案】解:,
当时,,
当时,有最大值,
当时,有最大值.
当时,射程有最大值,最大射程是;
,
设存在,,使两孔射出水的射程相同,则有:
,
,
,
,
,
,或,
或;
设垫高的高度为,则,
当时,,
,此时.
垫高的高度为,小孔离水面的竖直距离为.
【解析】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
将写成顶点式,按照二次函数的性质得出的最大值,再求的算术平方根即可;
设存在,,使两孔射出水的射程相同,则,利用因式分解变形即可得出答案;
设垫高的高度为,写出此时关于的函数关系式,根据二次函数的性质可得答案.
22.【答案】【小题】
【小题】
由可知,
图象开口向上,对称轴为,当时,最小,最小值为,
当时,最大,最大值为,
该总公司能获得的总利润单位:万元的范围为.
【解析】
解:根据题意,得;
见答案
23.【答案】【小题】
解:设与之间的函数关系式为,则解得
;
【小题】
消毒洗手液的每瓶利润不允许高于进价的,即.
由题意,得,
图象的对称轴为,开口向下,
当时,随的增大而增大,
又,当时,有最大值为.
故售价定为元时,该药店可获得的利润最大,最大利润元.
【解析】 见答案
见答案
24.【答案】【小题】
解:设这种药材的售价元与月份的函数关系式为,则解得;
【小题】
设,把代入,得,解得,,
设这种药材每千克的利润为元,则,
,对称轴为,
为正整数,当时,最大.
月份出售这种药材获利最大.
【解析】 见答案
见答案
25.【答案】【小题】
解:探究发现,,
依题意,得,
解得舍,,当时,.
答:飞机落到安全线时飞行的水平距离为;
【小题】
设发射平台相对于安全线的高度为,
飞机相对于安全线的飞行高度,
,,
当时,,解得;
当时,,解得,
.
答:发射平台相对于安全线的高度的变化范围是大于且小于.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3实际问题与二次函数人教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.长为,宽为的矩形,四个角上分别剪去边长为的小正方形,然后把四边折起来,做成底面积为的无盖的长方体盒子,则与之间的函数关系式为( )
A. B.
C. D.
2.一位篮球运动员在距离篮筐中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确落入篮筐内.已知篮筐中心距离地面高度为,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是 B. 篮筐中心的坐标是
C. 此抛物线的顶点坐标是 D. 篮球出手时离地面的高度是
3.赵州桥始建于隋代,是世界上现存年代最久远、跨度最大、保存最完整的单孔石拱桥.如图是一座仿赵州桥建造的抛物线形拱桥的示意图,正常水位时,水面宽,水位上涨到达警戒水位,此时水面宽,则正常水位时拱顶离水面的高度为( )
A. B. C. D.
4.某民俗旅游村为接待游客住宿,开设了有个床位的旅馆.若每个床位每天收费元,则床位可全部租出;若每个床位每天的收费提高元,则相应地减少了个床位的租出.如果每个床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每个床位每天最合适的收费是( )
A. 元 B. 元 C. 元 D. 元
5.某公园草坪的护栏是由段形状相同的抛物线组成的,为了牢固起见,每段护栏需按间距加设由不锈钢管做成的立柱如图,护栏的最高点距底部,则所需不锈钢立柱的总长度为( )
A. B. C. D.
6.如图,在中,,,,点从点出发,沿向点以的速度运动,同时点从点出发,沿向点以的速度运动,当点运动到点时,点,同时停止运动.在运动过程中,四边形的面积最小为( )
A. B. C. D.
7.如图,有一块边长为的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A. B. C. D.
8.如图,一边靠墙墙有足够长,其它三边用长的篱笆围成一个矩形花园,这个花园的最大面积是( )
A. B. C. D. 以上都不对
9.一种玻璃水杯的截面如图所示,其左右轮廓线,为某一抛物线的一部分,杯口,杯底,且,杯深,如图若盛有部分水的水杯倾斜即,水面正好经过点,则此时点到杯口的距离为( )
A. B. C. D.
10.如图,一抛物线型拱桥,当拱顶到水面的距离为时,水面宽度为,那么水位下降时,水面的宽度为
A.
B.
C.
D.
11.如图,已知矩形中,,,对角线相交于点,抛物线经过,,三点,点是矩形内抛物线上的动点.则与面积之和的最大值是( )
A. B. C. D.
12.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长为设矩形菜园的边的长为,面积为,其中有下列结论:
的取值范围为;
的长有两个不同的值满足该矩形菜园的面积为;
矩形菜园的面积的最大值为.
其中,正确结论的个数是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,若被击打的小球飞行高度单位:与飞行时间单位:之间具有的关系为,则小球从飞出到落地所用的时间为
14.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长的栅栏,设面积为,垂直于墙的一边长为米.则关于的函数关系式: 并写出自变量的取值范围
15.如图,一块矩形土地由篱笆围着,并且由一条与边平行的篱笆分开,已知篱笆的总长为篱笆的厚度忽略不计,当 时,矩形土地的面积最大.
16.如图所示为一座抛物线形拱桥,当拱桥顶离水面时,水面宽,则水面下降时,水面宽度增加
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
某商场销售一种成本为元的商品,市场调研反映:在某个月的第天的销售价格为元,日销售量与的函数关系如图所示.
求与的函数解析式;
销售该商品第几天时,日销售利润最大?
结合函数图象回答,在当月有多少天的日销售利润大于元?
18.本小题分
要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出的水与池中心的水平距离为,距地面的高度为测量得到如表数值:
小腾根据学习函数的经验,发现是的函数,并对随的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
在平面直角坐标系中,描出表中各组数值所对应的点,并画出函数的图象;
结合函数图象,出水口距地面的高度为______,水达到最高点时与池中心的水平距离约为______结果保留小数点后两位;
为了使水柱落地点与池中心的距离不超过,如果只调整水管的高度,其他条件不变,结合函数图象,估计出水口至少需要______填“升高”或“降低” ______结果保留小数点后两位.
19.本小题分
某商场销售一批名牌衬衫,平均每天可售出件,每件盈利元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价元,商场平均每天可多售出件.求:
若商场平均每天要盈利元,每件衬衫应降价多少元?
每件衬衫降价多少元时,商场平均每天盈利最多?
20.本小题分
某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距水枪水平距离为米的地点,水柱距离湖面高度为米.
米
米
请解决以下问题:
在下边网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
请结合表中所给数据或所画图象,估出喷泉的落水点距水枪的水平距离约为______米精确到;
公园增设了新的游玩项目,购置了宽度米,顶棚到水面高度为米的平顶游船,游船从喷泉正下方通过,别有一番趣味,请通过计算说明游船是否有被喷泉淋到的危险.
21.本小题分
用各种盛水容器可以制作精致的家用流水景观如图.
科学原理:如图,始终盛满水的圆体水桶水面离地面的高度为单位:,如果在离水面竖直距离为单位:的地方开大小合适的小孔,那么从小孔射出水的射程水流落地点离小孔的水平距离单位:与的关系为.
应用思考:现用高度为的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距高处开一个小孔.
写出与的关系式;并求出当为何值时,射程有最大值,最大射程是多少?
在侧面开两个小孔,这两个小孔离水面的竖直距离分别为,,要使两孔射出水的射程相同,求,之间的关系式;
如果想通过垫高塑料水瓶,使射出水的最大射程增加,求整高的高度及小孔离水面的竖直距离.
22.本小题分
某总公司准备投资,两子公司共万元,从公司可获得的利润万元与投入资金万元满足关系,从公司可获得的利润万元与投入资金万元满足关系,万元为投资万元获得的总利润,设其中投资公司万元.
投资公司 万元,投资万元获得总利润为 万元以上两空均用表示;
求该总公司能获得的总利润的取值范围.
23.本小题分
某药店的消毒洗手液很畅销.已知该消毒洗手液的进价为每瓶元,经市场调查,每天洗手液的销售量瓶与销售单价元瓶之间满足一次函数关系,部分数据记录如表所示:
元瓶
瓶
直接写出与之间的函数关系式;不需要写自变量的取值范围
该药店的上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的设这种消毒洗手液每天的总利润为元,那么售价定为多少元时,该药店可获得的利润最大?最大利润是多少元?
24.本小题分
某地的药材批发公司指导农民种植和销售某种药材,经市场调研发现:月份这种药材每千克的售价元与月份之间存在如表所示的一次函数关系,同时,每千克的成本价元与月份之间的函数关系图象近似满足如图所示的抛物线.
月份
每千克售价元
直接写出这种药材的售价元与月份的函数关系式;
试判断几月份出售这种药材获利最大?
25.本小题分
某课外科技活动小组研制了一种航模飞行,通过实验,收集了飞机相对于出发点的飞行水平距离单位:、飞行高度单位:随飞行时间单位:的变化数据如下表:
飞机时间
飞行水平距离
飞行高度
探究发现:与,与之间的数量关系可以用我们已学过的函数来描述,直接写出关于的函数解析式和关于的函数解析式不要求写出自变量的取值范围;
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机,根据上面的探究发现解决下列问题:
若发射平台相对于安全线的高度为,求飞机落到安全线时飞行的水平距离;
在安全线上设置回收区域,,若飞机落到内不包括端点,,求发射平台相对于安全线的高度的变化范围.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】略
3.【答案】
【解析】略
4.【答案】
【解析】设每个床位每天的收费提高个元,每天的租金为元.根据题意,得为整数,当或时,有最大值.为使租出的床位少且租金高,每个床位每天最合适的收费是元.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】【分析】
本题考查了二次函数的应用及二次函数的最值,设与墙垂直的矩形的边长为 ,从而列出面积为,利用二次函数的性质求解即可.
【解答】
解:设与墙垂直的矩形的边长为 ,
则这个花园的面积是:,
当时,取得最大值,此时,
故选:.
9.【答案】
【解析】【分析】
本题考查二次函数的应用,属于较难题.
以的中点为原点建立平面直角坐标系,求得轮廓线,所在抛物线的解析式,再求得直线的解析式,联立解得点的横坐标,即可求解到杯口的距离.
【解答】
解:以的中点为原点建立平面直角坐标系,设直线与轴交点为,
,,,,
设轮廓线,所在抛物线的解析式为,
把、代入得,,
,
,直线与轴交点为,
,,
设直线的解析式为,
把、代入得,,
直线的解析式为:
由解得,舍
当,,
此时点到杯口的距离为,
故选 D.
10.【答案】
【解析】解:以拱顶所在的直线为轴,以这座抛物线型拱桥的对称轴为轴,建立直角坐标系,
设抛物线解析式为,
把代入得:,
解得:,
抛物线解析式为,
水位下降时,
拱顶到水面的距离为
把代入得:,
则水面的宽度是米,
故选:.
根据题意设抛物线解析式,求出解析式确定出水面的宽度即可.
本题主要考查二次函数的应用,熟练掌握待定系数法是解本题的关键.
11.【答案】
【解析】【分析】
本题考查了待定系数法求函数解析式、矩形的性质、三角形的面积公式以及二次函数的最值,建立直角坐标系,找出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.以点为原点,线段所在的直线为轴,线段所在的直线为轴建立直角坐标系,根据长方形的性质得出点、、三点的坐标,设抛物线的解析式为,结合点、、的坐标利用待定系数法即可求出抛物线的解析式,由点为长方形内的抛物线上的动点,设出点的坐标,结合三角形的面积公式找出关于的函数解析式,根据二次函数的性质即可得出结论.
【解答】
解:以点为原点,线段所在的直线为轴,线段所在的直线为轴建立直角坐标系,如图所示.
矩形中,,,对角线相交于点,
点的坐标为,点的坐标为,点的坐标为.
设抛物线的解析式为,
抛物线经过、、三点,
有,
解得:,
抛物线的解析式为.
点是矩形内的抛物线上的动点,
设点的坐标为,
当时,与面积之和最大,最大值为.
故选B.
12.【答案】
【解析】解:设这个菜园垂直于墙的一边的长为则的长为米,
墙长为,,
解得,
的取值范围为,
故错误;
根据题意得:,
解得,,
,
,
的长有个值满足该矩形菜园的面积为,
故错误;
根据题意得:,
,,
当时,有最大值,最大值为,
故正确.
故选:.
根据墙长为,,列不等式组,解不等式组即可求出自变量的取值范围,从而可判断;根据矩形的面积列出方程,解方程求的值,可以判断;利用二次函数求最值的知识可得出菜园的最大面积,可以判断.
此题主要考查了二次函数及一元二次方程的应用,熟练掌握最值问题的求法是解答本题的关键.
13.【答案】
【解析】【分析】
本题考查的是二次函数的应用有关知识,根据关系式,令即可求得的值为飞行的时间.
【解答】
解:依题意,令得:
,
得,
解得舍去或,
即小球从飞出到落地所用的时间为.
故答案为.
14.【答案】.
【解析】【分析】
本题主要考查二次函数的应用.根据条件得出与旧墙平行的一边的长度是解决问题的关键.
根据题意可知,三间羊圈与旧墙平行的一边的总长为,列出二次函数的关系式即可.
【解答】
解:根据题意可知,三间羊圈与旧墙平行的一边的总长为,
则: 由图可知:,,
所以的取值范围是.
故答案为:.
15.【答案】
【解析】【分析】
本题考查二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的顶点式求函数的最值.
设,矩形土地的面积为,则,进而求出与的函数关系式,将其化为顶点式求最值即可.
【解答】
解:设,矩形土地的面积为,
则,
由题意可得,
,
当时,取得最大值,此时,
,
故答案为:.
16.【答案】
【解析】略
17.【答案】【小题】
解:设,
把,代入上式得,
解得,
与的函数解析式为:
【小题】
设日销售利润为元,
由题意得:
,
,,
当时,最大,
答:销售该商品第天时,日销售利润最大.
【小题】
令,
则,
解得,,,
结合二次函数图象可知,
当时,,
有天的日销售利润大于元.
【解析】
设,根据图象取两个点坐标代入,求出,的值即可.
设日销售利润为元,列出关于的函数关系式,求最大值即可.
令,求出一元二次方程的两个解,结合二次函数的草图求出的范围,从而得到结果.
本题主要考查了一次函数的应用,二次函数的应用,读懂题意,正确列出函数关系式是解题的关键.
18.【答案】解:如图,
设,
把代入可得,
,
解得,
所以与的关系式为,
当时,;顶点坐标为,
出水口距地面的高度为,水达到最高点时与池中心的水平距离约为,
故答案为:,;
当时,,
所以出水口至少要降低米,
故答案为:降低,.
【解析】本题考查二次函数的实际应用,根据点的坐标画出函数图象是解题关键.
根据对应点画出图象即可;
根据对应点求出与的关系式即可得到答案;
把代入得到得值可得出水口要升高的高度.
19.【答案】解:设每件衬衫应降价元,则每天多销售件,由题意,得
,
解得:,,
要扩大销售,减少库存,
每件衬衫应降价元;
设商场每天的盈利为元,由题意,得
,
,
时,最大元.
答:每件衬衫应降价元时,商场平均每天盈利最多,每天最多盈利元.
【解析】本题主要考查了二次函数的应用以及一元二次方程的应用,根据数量关系列出关于的一元二次方程二次函数关系式是解题的关键.
设每件衬衫应降价元,根据“商场盈利单件盈利销售数量”,即可列出关于的一元二次方程,解方程即可得出的值,再结合减少库存即可确定的值;
设每件衬衫降价元时,商场所获得的利润为元,根据“商场盈利单件盈利销售数量”,即可找出关于的二次函数关系式,配方后根据二次函数的性质即可得出每件衬衫降价多少元时盈利最大.
20.【答案】解:如图,
由图象得,顶点,
设,
把代入可得,
,
当时,,
解得或舍去,
米,
答:喷泉的落水点距水枪的水平距离约为米,
故答案为:;
当时,,
答:游船有被喷泉淋到的危险.
【解析】本题考查二次函数的实际应用,根据对应点的坐标得到二次函数关系式是解题关键.
根据对应点画图象即可;
求出二次函数的关系式,把代入即可;
把代入二次函数关系式得到得值,再与比较即可.
21.【答案】解:,
当时,,
当时,有最大值,
当时,有最大值.
当时,射程有最大值,最大射程是;
,
设存在,,使两孔射出水的射程相同,则有:
,
,
,
,
,
,或,
或;
设垫高的高度为,则,
当时,,
,此时.
垫高的高度为,小孔离水面的竖直距离为.
【解析】本题考查了二次函数在实际问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
将写成顶点式,按照二次函数的性质得出的最大值,再求的算术平方根即可;
设存在,,使两孔射出水的射程相同,则,利用因式分解变形即可得出答案;
设垫高的高度为,写出此时关于的函数关系式,根据二次函数的性质可得答案.
22.【答案】【小题】
【小题】
由可知,
图象开口向上,对称轴为,当时,最小,最小值为,
当时,最大,最大值为,
该总公司能获得的总利润单位:万元的范围为.
【解析】
解:根据题意,得;
见答案
23.【答案】【小题】
解:设与之间的函数关系式为,则解得
;
【小题】
消毒洗手液的每瓶利润不允许高于进价的,即.
由题意,得,
图象的对称轴为,开口向下,
当时,随的增大而增大,
又,当时,有最大值为.
故售价定为元时,该药店可获得的利润最大,最大利润元.
【解析】 见答案
见答案
24.【答案】【小题】
解:设这种药材的售价元与月份的函数关系式为,则解得;
【小题】
设,把代入,得,解得,,
设这种药材每千克的利润为元,则,
,对称轴为,
为正整数,当时,最大.
月份出售这种药材获利最大.
【解析】 见答案
见答案
25.【答案】【小题】
解:探究发现,,
依题意,得,
解得舍,,当时,.
答:飞机落到安全线时飞行的水平距离为;
【小题】
设发射平台相对于安全线的高度为,
飞机相对于安全线的飞行高度,
,,
当时,,解得;
当时,,解得,
.
答:发射平台相对于安全线的高度的变化范围是大于且小于.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
