三角形的外角
图片预览



文档简介
课件29张PPT。
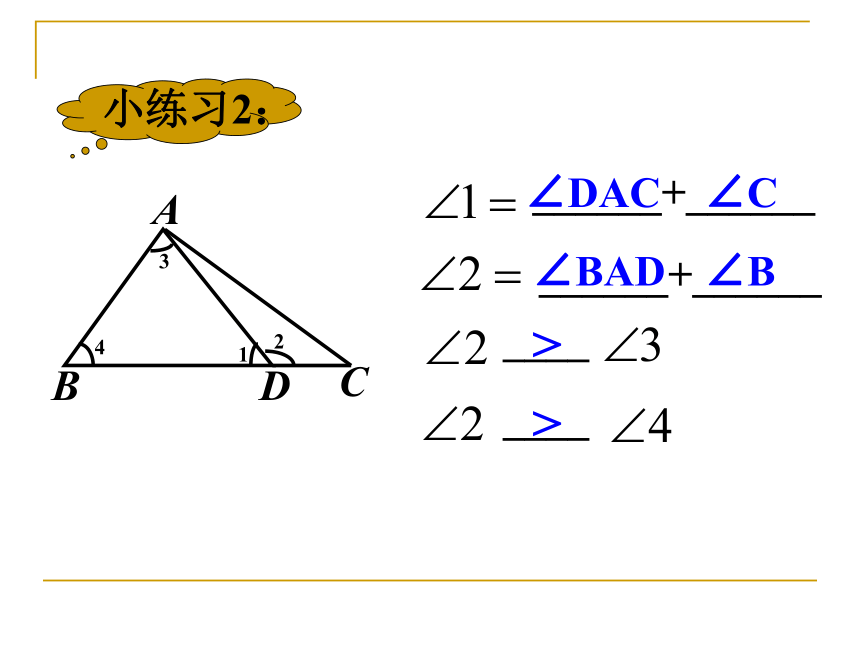
三角形的外角临海中学 初一数学备课组2、三角形的一个外角的性质(3)三角形的一个外角大于任何一个与它不相邻的内角。1、三角形的内角和180°三角形内角和外角的性质(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
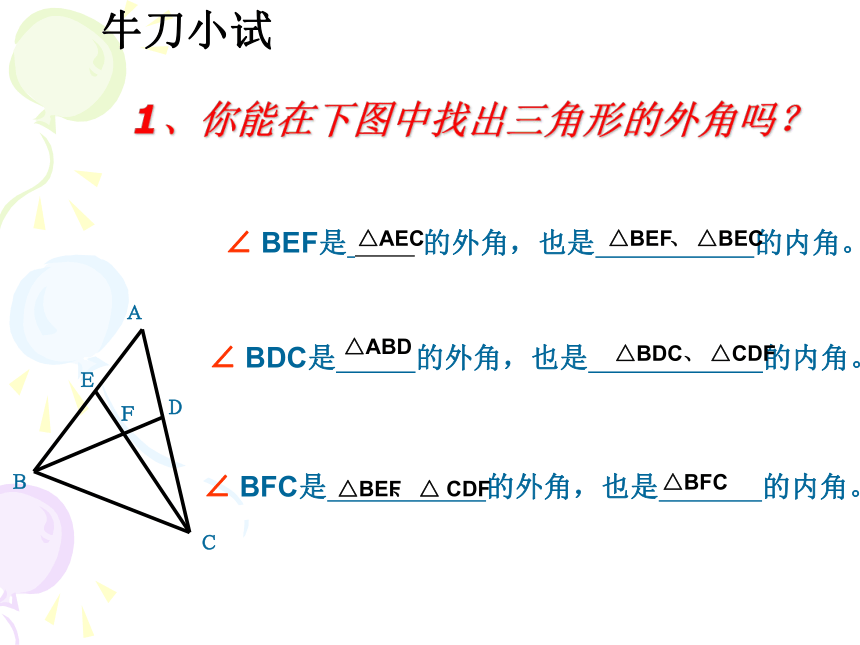
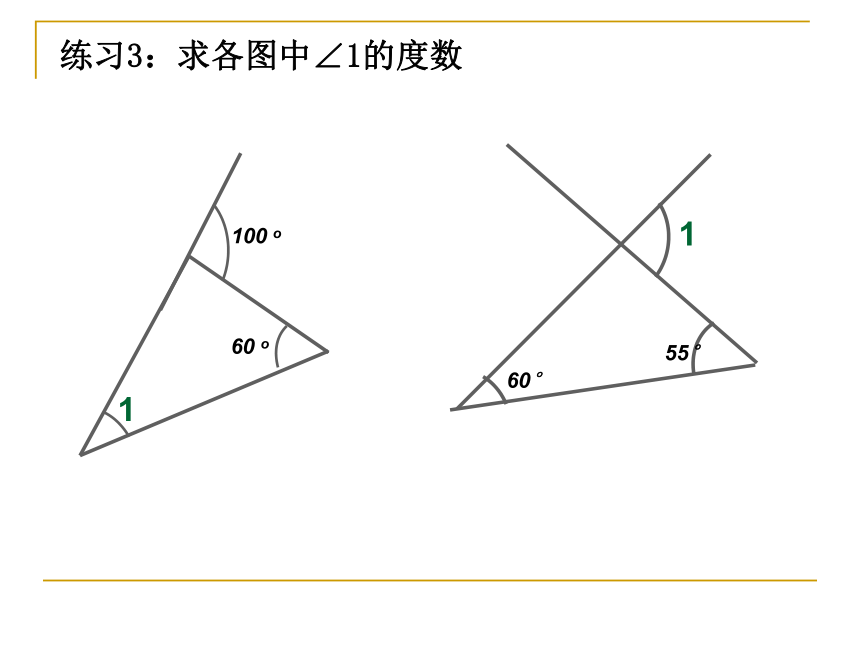
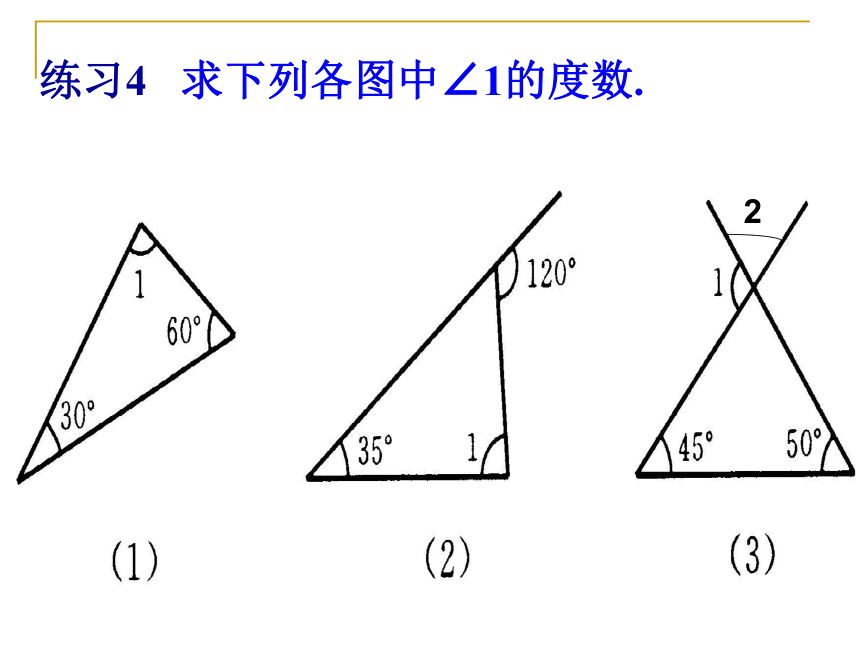
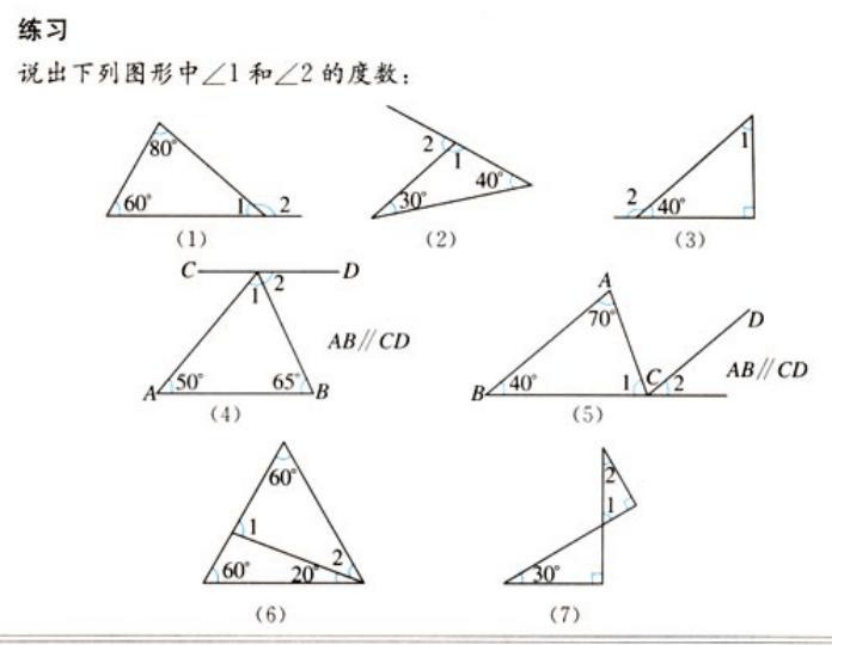
3、三角形的外角和等于360°。1、你能在下图中找出三角形的外角吗?∠ BEF是 的外角,也是 的内角。∠ BDC是 的外角,也是 的内角。∠ BFC是 的外角,也是 的内角。△AEC△BEF、 △BEC△ABD△BDC、 △CDF△BEF、 △ CDF△BFC牛刀小试>>练习3:求各图中∠1的度数练习4求下列各图中∠1的度数.2判断题:
1、三角形的一个外角等于两个内角的和。( )
2、三角形的一个外角等于与它不相邻的两个内角的和。( )
3、三角形的一个外角大于任何一个内角。( )
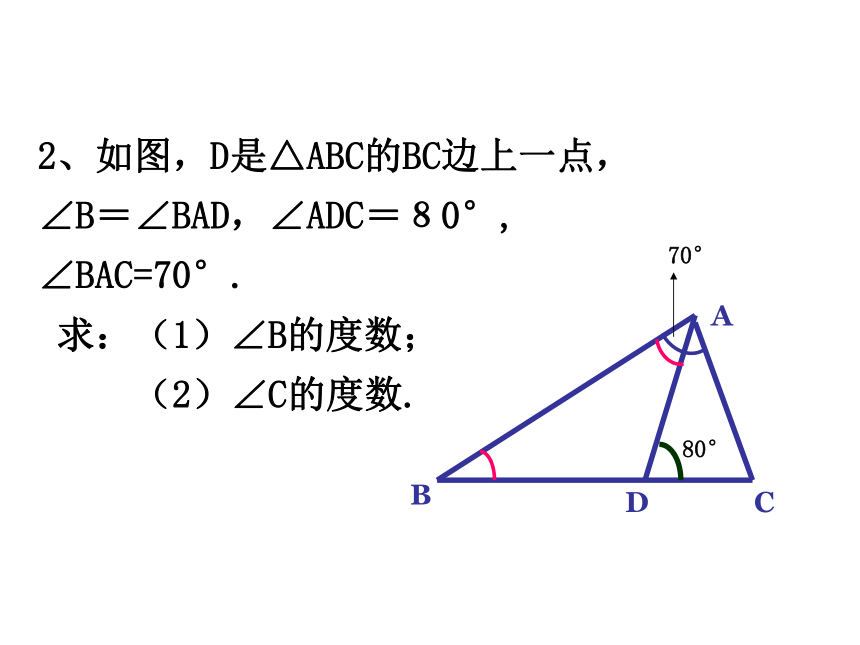
4、三角形的一个内角小于任何一个与它不相邻的外角。( )过关测试2、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列4、探究题:
(1)用牛皮筋拉成如下形状,若∠C=30°,你能
够求出∠A+ ∠B+ ∠D+ ∠E的值吗?
如果可以求出值,如果不可以,
请你说明理由。(2)求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数(3)求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数生活如此美妙!
我们正在拥有!!
一个个奇迹存在于细致的发现之中!!!
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACE与内角有什么关系?是∠ACB的邻补角.ABCE三角形的外角D∠ACD+ ∠ACB=180°∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:D解:过C作CE平行于ABABC∠1= ∠B∠2= ∠A∠1+ ∠2= ∠A+ ∠B即∠ACD= ∠A+ ∠B ∠1+∠2 +∠3 = ?
从哪些途径探究这个结果?议一议321ABC三角形的外角和等于360°三角形的内角 三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 温故而知新1在一个三角形中至少有()
(A)一个锐角 (B)一个直角
(C)一个钝角 (D)两个锐角
2一个三角形三个内角度数的比为3:4:5,那么这个三角形是()
(A)锐角三角形(B)直角三角形
(C)钝角三角形(D)等边三角形
3等腰三角形中有一个角是50°,则另外两个角是多少度?
4一个三角形两边相等,周长为20cm,三角形的一边长6cm,求其它两边长。
ABCEABC1E1观察∠
1外角相邻内角不相邻内角BAC123456其中, ∠4和∠3是三角形在顶点A的一对外角,他们是对顶角,通常说三角形的外角时,每个顶点处取一个外角。根据图形计算∠ CBD的大小,通过计算,你发现了什么规律? D 350700800400内角与外角有什么关系?(1) 相邻:发现:即:∠CBD(外角)+∠ABC(相邻内角)=180° 思考:如何说明∠ACD= ∠B+ ∠ AD三角形的一个外角与三角形三个内角之间有何关系?三角形的一个外角等于与它不相邻的两个内角的和。三角形的外角大于任何一个与它不相邻的内角。∠ACD> ∠ B∠ACD> ∠ A12 这里只介绍了两种求解思路,课后可通过小组讨论探究求解该问题的另外的方法。FGABCDE12F4例1 已知:如图,在△ABC中,AD平分
外角∠EAC,∠B= ∠C. 则AD ∥ BC
请说明理由.解∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和), ∴ AD∥BC (内错角相等,两直线平行). ∠B=∠C (已知), ∴∠DAC=∠C(等量代换). ∵ AD平分 ∠EAC(已知).∴∠C= ∠EAC∴∠DAC= ∠EAC(角平分线的定义).··
三角形的外角临海中学 初一数学备课组2、三角形的一个外角的性质(3)三角形的一个外角大于任何一个与它不相邻的内角。1、三角形的内角和180°三角形内角和外角的性质(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
3、三角形的外角和等于360°。1、你能在下图中找出三角形的外角吗?∠ BEF是 的外角,也是 的内角。∠ BDC是 的外角,也是 的内角。∠ BFC是 的外角,也是 的内角。△AEC△BEF、 △BEC△ABD△BDC、 △CDF△BEF、 △ CDF△BFC牛刀小试>>练习3:求各图中∠1的度数练习4求下列各图中∠1的度数.2判断题:
1、三角形的一个外角等于两个内角的和。( )
2、三角形的一个外角等于与它不相邻的两个内角的和。( )
3、三角形的一个外角大于任何一个内角。( )
4、三角形的一个内角小于任何一个与它不相邻的外角。( )过关测试2、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列4、探究题:
(1)用牛皮筋拉成如下形状,若∠C=30°,你能
够求出∠A+ ∠B+ ∠D+ ∠E的值吗?
如果可以求出值,如果不可以,
请你说明理由。(2)求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数(3)求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数生活如此美妙!
我们正在拥有!!
一个个奇迹存在于细致的发现之中!!!
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACE与内角有什么关系?是∠ACB的邻补角.ABCE三角形的外角D∠ACD+ ∠ACB=180°∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:D解:过C作CE平行于ABABC∠1= ∠B∠2= ∠A∠1+ ∠2= ∠A+ ∠B即∠ACD= ∠A+ ∠B ∠1+∠2 +∠3 = ?
从哪些途径探究这个结果?议一议321ABC三角形的外角和等于360°三角形的内角 三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 温故而知新1在一个三角形中至少有()
(A)一个锐角 (B)一个直角
(C)一个钝角 (D)两个锐角
2一个三角形三个内角度数的比为3:4:5,那么这个三角形是()
(A)锐角三角形(B)直角三角形
(C)钝角三角形(D)等边三角形
3等腰三角形中有一个角是50°,则另外两个角是多少度?
4一个三角形两边相等,周长为20cm,三角形的一边长6cm,求其它两边长。
ABCEABC1E1观察∠
1外角相邻内角不相邻内角BAC123456其中, ∠4和∠3是三角形在顶点A的一对外角,他们是对顶角,通常说三角形的外角时,每个顶点处取一个外角。根据图形计算∠ CBD的大小,通过计算,你发现了什么规律? D 350700800400内角与外角有什么关系?(1) 相邻:发现:即:∠CBD(外角)+∠ABC(相邻内角)=180° 思考:如何说明∠ACD= ∠B+ ∠ AD三角形的一个外角与三角形三个内角之间有何关系?三角形的一个外角等于与它不相邻的两个内角的和。三角形的外角大于任何一个与它不相邻的内角。∠ACD> ∠ B∠ACD> ∠ A12 这里只介绍了两种求解思路,课后可通过小组讨论探究求解该问题的另外的方法。FGABCDE12F4例1 已知:如图,在△ABC中,AD平分
外角∠EAC,∠B= ∠C. 则AD ∥ BC
请说明理由.解∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和), ∴ AD∥BC (内错角相等,两直线平行). ∠B=∠C (已知), ∴∠DAC=∠C(等量代换). ∵ AD平分 ∠EAC(已知).∴∠C= ∠EAC∴∠DAC= ∠EAC(角平分线的定义).··
